Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Davies, P. L.
1973.
Everywhere irregularity of certain classes of random processes with stationary Gaussian increments.
Advances in Applied Probability,
Vol. 5,
Issue. 1,
p.
103.
Berman, Simeon M.
1973.
Local nondeterminism and local times of Gaussian processes.
Bulletin of the American Mathematical Society,
Vol. 79,
Issue. 2,
p.
475.
Davies, P. L.
1973.
Everywhere irregularity of certain classes of random processes with stationary Gaussian increments.
Advances in Applied Probability,
Vol. 5,
Issue. 1,
p.
103.
Hawkes, John
1977.
Local properties of some Gaussian processes.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 40,
Issue. 4,
p.
309.
Kôno, Norio
1977.
Hölder conditions for the local times of certain Gaussian processes with stationary increments.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 53,
Issue. 3,
Ehm, W.
1981.
Sample function properties of multi-parameter stable processes.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 56,
Issue. 2,
p.
195.
Graversen, S. E.
1982.
“Polar”-functions for Brownian motion.
Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 61,
Issue. 2,
p.
261.
Berman, Simeon M.
1983.
Nonincrease almost everywhere of certain measurable functions with applications to stochastic processes.
Proceedings of the American Mathematical Society,
Vol. 88,
Issue. 1,
p.
141.
Taylor, S. James
1986.
The measure theory of random fractals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 3,
p.
383.
Monrad, Ditlev
and
Pitt, Loren D.
1987.
Seminar on Stochastic Processes, 1986.
p.
163.
Bertoin, Jean
1990.
Hausdorff dimension of the level sets for self-affine functions.
Japan Journal of Applied Mathematics,
Vol. 7,
Issue. 2,
p.
197.
Kôno, N.
1994.
Nowhere differentiable functions constructed from probabilistic point of view.
Acta Mathematica Hungarica,
Vol. 65,
Issue. 3,
p.
285.
Monrad, Ditlev
and
Rootzén, Holger
1995.
Small values of Gaussian processes and functional laws of the iterated logarithm.
Probability Theory and Related Fields,
Vol. 101,
Issue. 2,
p.
173.
Csörgő, Miklós
Lin, Zheng-Yan
and
Shao, Qi-Man
1995.
On moduli of continuity for local times of Gaussian processes.
Stochastic Processes and their Applications,
Vol. 58,
Issue. 1,
p.
1.
Dozzi, Marco
and
Soltani, A.Reza
1997.
Local time for stable moving average processes: Hölder conditions.
Stochastic Processes and their Applications,
Vol. 68,
Issue. 2,
p.
195.
Anh, V.
Lunney, K.
and
Peiris, S.
1997.
Stochastic models for characterisation and prediction of time series with long-range dependence and fractality.
Environmental Modelling & Software,
Vol. 12,
Issue. 1,
p.
67.
Nasyrov, F. S.
1997.
On Local Times for Functions and StochasticProcesses.
Theory of Probability & Its Applications,
Vol. 41,
Issue. 2,
p.
275.
Anh, V.V.
Heyde, C.C.
and
Tieng, Q.
1999.
Stochastic models for fractal processes.
Journal of Statistical Planning and Inference,
Vol. 80,
Issue. 1-2,
p.
123.
Khoshnevisan, Davar
Xiao, Yimin
and
Zhong, Yuquan
2003.
Local times of additive Lévy processes.
Stochastic Processes and their Applications,
Vol. 104,
Issue. 2,
p.
193.
Boufoussi, B.
Dozzi, M.
and
Guerbaz, R.
2006.
On the local time of multifractional Brownian motion.
Stochastics,
Vol. 78,
Issue. 1,
p.
33.


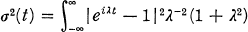 dH(λ), for some bounded monotone
dH(λ), for some bounded monotone 