Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T05:21:16.877Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GAMMA CONSTRUCTION AND ASYMPTOTIC INVARIANTS OF LINE BUNDLES OVER ARBITRARY FIELDS

Part of: Local theory General commutative ring theory Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  23 September 2019

TAKUMI MURAYAMA Open the ORCID record for TAKUMI MURAYAMA [Opens in a new window]
TAKUMI MURAYAMA*
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544-1000, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend results on asymptotic invariants of line bundles on complex projective varieties to projective varieties over arbitrary fields. To do so over imperfect fields, we prove a scheme-theoretic version of the gamma construction of Hochster and Huneke to reduce to the setting where the ground field is 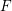$F$-finite. Our main result uses the gamma construction to extend the ampleness criterion of de Fernex, Küronya, and Lazarsfeld using asymptotic cohomological functions to projective varieties over arbitrary fields, which was previously known only for complex projective varieties. We also extend Nakayama’s description of the restricted base locus to klt or strongly 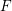$F$-regular varieties over arbitrary fields.

MSC classification

Primary: 14C20: Divisors, linear systems, invertible sheaves
Secondary: 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 14F17: Vanishing theorems 14B05: Singularities
Type
Article
Information
Nagoya Mathematical Journal , Volume 242 , June 2021 , pp. 165 - 207
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This material is based upon work supported by the National Science Foundation under grant nos. DMS-1501461 and DMS-1701622.

References

Angehrn, U. and Siu, Y. T., Effective freeness and point separation for adjoint bundles, Invent. Math. 122 (1995), 291–308.Google Scholar
Avramov, L. L., Flat morphisms of complete intersections, Soviet Math. Dokl. 16 (1975), 1413–1417; Translated from the Russian by D. L. Johnson.Google Scholar
Bingener, J. and Flenner, H., “On the fibers of analytic mappings”, in Complex Analysis and Geometry, Univ. Ser. Math., Plenum, New York, 1993, 45–101.Google Scholar
Birkar, C., The augmented base locus of real divisors over arbitrary fields, Math. Ann. 368 (2017), 905–921.Google Scholar
Boucksom, S., Broustet, A. and Pacienza, G., Uniruledness of stable base loci of adjoint linear systems via Mori theory, Math. Z. 275 (2013), 499–507.Google Scholar
Burgos Gil, J. I., Gubler, W., Jell, P., Künnemann, K. and Martin, F., Differentiability of non-archimedean volumes and non-archimedean Monge–Ampère equations, Algebr. Geom. (2019), to appear, With an appendix by R. Lazarsfeld, arXiv:1608.01919v6 [math.AG].Google Scholar
Cacciola, S. and Di Biagio, L., Asymptotic base loci on singular varieties, Math. Z. 275 (2013), 151–166.Google Scholar
Cutkosky, S. D., Teissier’s problem on inequalities of nef divisors, J. Algebra Appl. 14 (2015), 1540002, 37 pp.Google Scholar
Datta, R. and Murayama, T., Permanence properties of $F$-injectivity, preprint, 2019. arXiv:1906.11399v1 [math.AC].Google Scholar
Datta, R. and Smith, K. E., Frobenius and valuation rings, Algebra Number Theory 10 (2016), 1057–1090; See also [11].Google Scholar
Datta, R. and Smith, K. E., Correction to the article “Frobenius and valuation rings”, Algebra Number Theory 11 (2017), 1003–1007.Google Scholar
de Fernex, T., Küronya, A. and Lazarsfeld, R., Higher cohomology of divisors on a projective variety, Math. Ann. 337 (2007), 443–455.Google Scholar
de Fernex, T. and Mustaţă, M., Limits of log canonical thresholds, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 491–515.Google Scholar
Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M., Asymptotic invariants of line bundles, Pure Appl. Math. Q. 1 (2005), 379–403.Google Scholar
Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M., Asymptotic invariants of base loci, Ann. Inst. Fourier (Grenoble) 56 (2006), 1701–1734.Google Scholar
Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M., Restricted volumes and base loci of linear series, Amer. J. Math. 131 (2009), 607–651.Google Scholar
Enescu, F. and Hochster, M., The Frobenius structure of local cohomology, Algebra Number Theory 2 (2008), 721–754.Google Scholar
Fedder, R., F-purity and rational singularity, Trans. Amer. Math. Soc. 278 (1983), 461–480.Google Scholar
Fedder, R. and Watanabe, K.-i., “A characterization of F-regularity in terms of F-purity”, in Commutative Algebra (Berkeley, CA, 1987), Math. Sci. Res. Inst. Publ. 15, Springer, New York, 1989, 227–245.Google Scholar
Flenner, H., O’Carroll, L. and Vogel, W., Joins and Intersections, Springer Monogr. Math., Springer, Berlin, 1999.Google Scholar
Fulger, M., Kollár, J. and Lehmann, B., Volume and Hilbert function of ℝ-divisors, Michigan Math. J. 65 (2016), 371–387.Google Scholar
Gabber, O., “Notes on some t-structures”, in Geometric Aspects of Dwork Theory. Vol. II, Walter de Gruyter, Berlin, 2004, 711–734.Google Scholar
Grothendieck, A., Séminaire de géométrie algébrique du Bois Marie, 1962. Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Doc. Math. (Paris), 4, Soc. Math. France, Paris, 2005, With an exposé by Mme M. Raynaud, With a preface and edited by Y. Laszlo, Revised reprint of the 1968 French original.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 1–231.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 1–255.Google Scholar
Hara, N. and Takagi, S., On a generalization of test ideals, Nagoya Math. J. 175 (2004), 59–74.Google Scholar
Hara, N. and Yoshida, K., A generalization of tight closure and multiplier ideals, Trans. Amer. Math. Soc. 355 (2003), 3143–3174.Google Scholar
Hartshorne, R., Residues and Duality, Lecture Notes in Mathematics, 20, Springer, Berlin–New York, 1966, Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64, With an appendix by P. Deligne.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52, Springer, New York–Heidelberg, 1977.Google Scholar
Hashimoto, M., F-pure homomorphisms, strong F-regularity, and F-injectivity, Comm. Algebra 38 (2010), 4569–4596.Google Scholar
Hashimoto, M., “F-purity of homomorphisms, strong F-regularity, and F-injectivity”, in The 31st Symposium on Commutative Algebra in Japan (Osaka, 2009), 2010, 9–16. http://www.math.okayama-u.ac.jp/∼hashimoto/paper/Comm-Alg/31-all.pdf.Google Scholar
Hauser, H., On the problem of resolution of singularities in positive characteristic (or: a proof we are still waiting for), Bull. Amer. Math. Soc. (N.S.) 47 (2010), 1–30.Google Scholar
Hochster, M. and Huneke, C., Tight closure, invariant theory, and the Briançon–Skoda theorem, J. Amer. Math. Soc. 3 (1990), 31–116.Google Scholar
Hochster, M. and Huneke, C., F-regularity, test elements, and smooth base change, Trans. Amer. Math. Soc. 346 (1994), 1–62.Google Scholar
Hochster, M. and Roberts, J. L., Rings of invariants of reductive groups acting on regular rings are Cohen–Macaulay, Adv. Math. 13 (1974), 115–175.Google Scholar
Hochster, M. and Roberts, J. L., The purity of the Frobenius and local cohomology, Adv. Math. 21 (1976), 117–172.Google Scholar
Ito, A., Okounkov bodies and Seshadri constants, Adv. Math. 241 (2013), 246–262.Google Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.Google Scholar
Jonsson, M. and Mustaţă, M., Valuations and asymptotic invariants for sequences of ideals, Ann. Inst. Fourier (Grenoble) 62 (2012), 2145–2209.Google Scholar
Kleiman, S. L., “The Picard scheme”, in Fundamental Algebraic Geometry, Math. Surveys Monographs, 123, American Mathematical Society, Providence, RI, 2005, 235–321.Google Scholar
Küronya, A., Asymptotic cohomological functions on projective varieties, Amer. J. Math. 128 (2006), 1475–1519.Google Scholar
Kunz, E., On Noetherian rings of characteristic p, Amer. J. Math. 98 (1976), 999–1013.Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. I. Classical Setting: Line Bundles and Linear Series, Ergeb. Math. Grenzgeb. (3), 48, Springer, Berlin, 2004.Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. II. Positivity for Vector Bundles, and Multiplier Ideals, Ergeb. Math. Grenzgeb. (3), 49, Springer, Berlin, 2004.Google Scholar
Ma, L., Finiteness properties of local cohomology for F-pure local rings, Int. Math. Res. Not. IMRN 20 (2014), 5489–5509.Google Scholar
Ma, L., Polstra, T., Schwede, K. and Tucker, K., F-signature under birational morphisms, Forum Math. Sigma 7 (2019), e11, 20 pp.Google Scholar
Manaresi, M., Some properties of weakly normal varieties, Nagoya Math. J. 77 (1980), 61–74.Google Scholar
Matsumura, H., Commutative Ring Theory, 2nd ed., Cambridge Stud. Adv. Math., 8, Cambridge University Press, Cambridge, 1989, Translated from the Japanese by M. Reid.Google Scholar
Murayama, T., Frobenius–Seshadri constants and characterizations of projective space, Math. Res. Lett. 25 (2018), 905–936.Google Scholar
Murayama, T., Seshadri constants and Fujita’s conjecture via positive characteristic methods, Ph.D. thesis, University of Michigan, Ann Arbor, 2019, 206 pp.Google Scholar
Mustaţă, M., “The non-nef locus in positive characteristic”, in A Celebration of Algebraic Geometry, Clay Math. Proc., 18, American Mathematical Society, Providence, RI, 2013, 535–551.Google Scholar
Nakayama, N., Zariski-decomposition and abundance, MSJ Mem. 14, Math. Soc. Japan, Tokyo, 2004.Google Scholar
Nayak, S., Compactification for essentially finite-type maps, Adv. Math. 222 (2009), 527–546.Google Scholar
Patakfalvi, Zs., Schwede, K. and Tucker, K., “Positive characteristic algebraic geometry”, in Surveys on Recent Developments in Algebraic Geometry, Proc. Sympos. Pure Math., 95, American Mathematical Society, Providence, RI, 2017, 33–80.Google Scholar
Quy, P. H. and Shimomoto, K., F-injectivity and Frobenius closure of ideals in Noetherian rings of characteristic p > 0, Adv. Math. 313 (2017), 127–166.+0,+Adv.+Math.+313+(2017),+127–166.>Google Scholar
Raynaud, M., “Contre-exemple au ‘vanishing theorem’ en caractéristique p > 0”, in C. P. Ramanujam—A Tribute, Tata Inst. Fund. Res. Studies in Math., 8, Springer, Berlin–New York, 1978, 273–278.+0”,+in+C.+P.+Ramanujam—A+Tribute,+Tata+Inst.+Fund.+Res.+Studies+in+Math.,+8,+Springer,+Berlin–New+York,+1978,+273–278.>Google Scholar
Sato, K., Stability of test ideals of divisors with small multiplicity, Math. Z. 288 (2018), 783–802.Google Scholar
Schwede, K., F-injective singularities are Du Bois, Amer. J. Math. 131 (2009), 445–473.Google Scholar
Schwede, K., Centers of F-purity, Math. Z. 265 (2010), 687–714.Google Scholar
Schwede, K., Test ideals in non-ℚ-Gorenstein rings, Trans. Amer. Math. Soc. 363 (2011), 5925–5941.Google Scholar
Schwede, K. and Tucker, K., “A survey of test ideals”, in Progress in Commutative Algebra 2, Walter de Gruyter, Berlin, 2012, 39–99.Google Scholar
Takagi, S. and Watanabe, K.-i., F-singularities: applications of characteristic p methods to singularity theory, Sugaku Expositions 31 (2018), 1–42; Translated from the Japanese by the authors.Google Scholar
Tanaka, H., Semiample perturbations for log canonical varieties over an F-finite field containing an infinite perfect field, Internat. J. Math. 28 (2017), 1750030, 13 pp.Google Scholar
Tanaka, H., Minimal model program for excellent surfaces, Ann. Inst. Fourier (Grenoble) 68 (2018), 345–376.Google Scholar
Tanaka, H., Abundance theorem for surfaces over imperfect fields, Math. Z. (2019), to appear arXiv:1502.01383v5 [math.AG], doi:10.1007/s00209-019-02345-2.Google Scholar
Vélez, J. D., Openness of the F-rational locus and smooth base change, J. Algebra 172 (1995), 425–453.Google Scholar