Published online by Cambridge University Press: 29 November 2021
Let
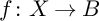 $f\colon X\to B$
be a semistable fibration where X is a smooth variety of dimension
$f\colon X\to B$
be a semistable fibration where X is a smooth variety of dimension
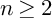 $n\geq 2$
and B is a smooth curve. We give the structure theorem for the local system of the relative
$n\geq 2$
and B is a smooth curve. We give the structure theorem for the local system of the relative
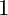 $1$
-forms and of the relative top forms. This gives a neat interpretation of the second Fujita decomposition of
$1$
-forms and of the relative top forms. This gives a neat interpretation of the second Fujita decomposition of
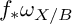 $f_*\omega _{X/B}$
. We apply our interpretation to show the existence, up to base change, of higher irrational pencils and on the finiteness of the associated monodromy representations under natural Castelnuovo-type hypothesis on local subsystems. Finally, we give a criterion to have that X is not of Albanese general type if
$f_*\omega _{X/B}$
. We apply our interpretation to show the existence, up to base change, of higher irrational pencils and on the finiteness of the associated monodromy representations under natural Castelnuovo-type hypothesis on local subsystems. Finally, we give a criterion to have that X is not of Albanese general type if
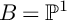 $B=\mathbb {P}^1$
.
$B=\mathbb {P}^1$
.
Luca Rizzi is supported by the Japan Society for the Promotion of Science, Postdoctoral Fellowship for Research in Japan. Francesco Zucconi is supported by the project “Progetti di Ricerca di Rilevante Interesse Nazionale, Geometric Analytic and Algebraic Aspects of Arithmetic.”