Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-25T14:54:09.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of functions in weighted sobolev spaces

Published online by Cambridge University Press:  22 January 2016

Toshihide Futamura  and
Yoshihiro Mizuta
Toshihide Futamura
Affiliation:
Department of Mathematics, Faculty of Science, Hiroshima University, Higashi-Hiroshima 739-8526, Japan
Yoshihiro Mizuta
Affiliation:
The Division of Mathematical and Information Sciences, Faculty of Integrated Arts and Sciences, Hiroshima University, Higashi-Hiroshima 739-8521, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to determine when there exists a quasicontinuous Sobolev function 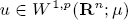whose trace 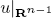is the characteristic function of a bounded set 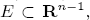where 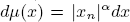with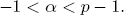

As application we discuss the existence of harmonic measures for weighted p-Laplacians in the unit ball.

Keywords

31B30
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 164 , December 2001 , pp. 75 - 88
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2001

References

[1] Carleson, L., Selected problems on exceptional sets, Van Nostrand, Princeton, 1967.Google Scholar
[2] Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions, Studies in Advanced Mathematics, CRC Press, 1992.Google Scholar
[3] Heinonen, J., Kilpeläinen, T. and Martio, O., Nonlinear potential theory of degenerate elliptic equations, Oxford Univ. Press, 1993.Google Scholar
[4] Herron, D. A. and Koskela, P., Continuity of Sobolev functions and Dirichlet finite harmonic measures, Potential Analysis, 6 (1997), 347-353.Google Scholar
[5] Meyers, N. G., A theory of capacities for potentials in Lebesgue classes, Math. Scand., 26 (1970), 255-292.Google Scholar
[6] Meyers, N. G., Continuity properties of potentials, Duke Math. J., 42 (1975), 157-166.CrossRefGoogle Scholar
[7] Mizuta, Y., Integral representations of Beppo Levi functions of higher order, Hiroshima Math. J., 4 (1974), 375-396.Google Scholar
[8] Mizuta, Y., On removable singularities of harmonic functions in U, Memoirs of the Faculty of Integrated Arts and Sciences, Hiroshima University, Ser. IV, Vol. 9 (1984) 9-21.Google Scholar
[9] Mizuta, Y., Potential theory in Euclidean spaces, Gakkōtosyo, Tokyo, 1996.Google Scholar
[10] Nakai, M., Dirichlet finite harmonic measures on Riemann surfaces, Complex Vari ables, 17 (1991), 123-131.Google Scholar
[11] Nakai, M., Existence of Dirichlet finite harmonic measures in non-linear potential the ory, Complex Variables, 21 (1993), 107-114.Google Scholar
[12] Nakai, M., Existence of Dirichlet finite harmonic measures on the Euclidean balls, Nagoya Math. J., 133 (1994), 85-125.Google Scholar
[13] Stein, E. M., Singular integrals and differentiability properties of functions, Princeton Univ. Press, Princeton, 1970.Google Scholar