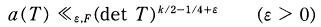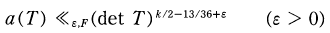Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kohnen, W.
1993.
On poincaré series of exponential type on sp2.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 63,
Issue. 1,
p.
283.
Böcherer, Siegfried
and
Kohnen, Winfried
1993.
Estimates for Fourier coefficients of Siegel cusp forms.
Mathematische Annalen,
Vol. 297,
Issue. 1,
p.
499.
Horie, T.
1997.
A Generalization of kohnen’s estimates for fourier coefficients of siegel cusp forms.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 67,
Issue. 1,
p.
47.
Bröker, Reinier
and
Lauter, Kristin
2014.
Evaluating Igusa functions.
Mathematics of Computation,
Vol. 83,
Issue. 290,
p.
2977.
Schulze-Pillot, Rainer
2017.
Averages of Fourier coefficients of Siegel modular forms and representation of binary quadratic forms by quadratic forms in four variables.
Mathematische Annalen,
Vol. 368,
Issue. 3-4,
p.
923.
Jha, Abhash Kumar
and
Sahu, Brundaban
2017.
Rankin–Cohen brackets on Siegel modular forms and special values of certain Dirichlet series.
The Ramanujan Journal,
Vol. 44,
Issue. 1,
p.
63.
Kohnen, Winfried
2022.
On the growth of Fourier coefficientsof Siegel cusp forms of degree two.
Research in the Mathematical Sciences,
Vol. 9,
Issue. 3,
Paul, Biplab
and
Saha, Abhishek
2023.
On Fourier Coefficients and Hecke Eigenvalues of Siegel Cusp Forms of Degree 2.
International Mathematics Research Notices,
Vol. 2023,
Issue. 24,
p.
21707.
Kumar, Balesh
and
Paul, Biplab
2023.
Additive twists of L2-norm of Fourier–Jacobi coefficients of Siegel cusp forms.
Journal of Number Theory,
Vol. 251,
Issue. ,
p.
70.
Babita
Jha, Abhash Kumar
Juyal, Abhishek
and
Maji, Bibekananda
2024.
An asymptotic expansion for a Lambert series associated with Siegel cusp forms.
The Ramanujan Journal,
Vol. 64,
Issue. 4,
p.
1199.
Jha, Abhash Kumar
and
Sarkar, Animesh
2025.
Fourier coefficients of Jacobi Poincaré series and applications.
Journal of Mathematical Analysis and Applications,
Vol. 543,
Issue. 2,
p.
128994.