No CrossRef data available.
Article contents
DYNAMICAL SYSTEMS ON SOME ELLIPTIC MODULAR SURFACES VIA OPERATORS ON LINE ARRANGEMENTS
Published online by Cambridge University Press: 20 January 2025
Abstract
This paper further studies the matroid realization space of a specific deformation of the regular n-gon with its lines of symmetry. Recently, we obtained that these particular realization spaces are birational to the elliptic modular surfaces 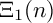 $\Xi _{1}(n)$ over the modular curve
$\Xi _{1}(n)$ over the modular curve 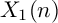 $X_1(n)$. Here, we focus on the peculiar cases when
$X_1(n)$. Here, we focus on the peculiar cases when 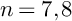 $n=7,8$ in more detail. We obtain concrete quartic surfaces in
$n=7,8$ in more detail. We obtain concrete quartic surfaces in 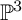 $\mathbb {P}^3$ equipped with a dominant rational self-map stemming from an operator on line arrangements, which yields K3 surfaces with a dynamical system that is semi-conjugated to the plane.
$\mathbb {P}^3$ equipped with a dominant rational self-map stemming from an operator on line arrangements, which yields K3 surfaces with a dynamical system that is semi-conjugated to the plane.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal



