Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-21T01:33:49.777Z Has data issue: false hasContentIssue false
  • English
  • Français

DUAL NAKANO POSITIVITY AND SINGULAR NAKANO POSITIVITY OF DIRECT IMAGE SHEAVES

Part of: Holomorphic fiber spaces (Co)homology theory Deformations of analytic structures

Published online by Cambridge University Press:  25 November 2024

YUTA WATANABE Open the ORCID record for YUTA WATANABE [Opens in a new window]
YUTA WATANABE*
Affiliation:
Department of Mathematics, Faculty of Science and Engineering Chuo University 1-13-27 Kasuga, Bunkyo-ku Tokyo 112-8551 Japan [email protected]
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 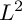$f:X\to Y$ be a surjective projective map, and let L be a holomorphic line bundle on X equipped with a (singular) semi-positive Hermitian metric h. In this article, by studying the canonical metric on the direct image sheaf of the twisted relative canonical bundles $K_{X/Y}\otimes L\otimes \mathscr {I}(h)$, we obtain that this metric has dual Nakano semi-positivity when h is smooth and there is no deformation by f and that this metric has locally Nakano semi-positivity in the singular sense when h is singular.

Keywords

direct image sheavesNakano positivitysingular Hermitian metricsL2-estimates

MSC classification

Primary: 32L10: Sheaves and cohomology of sections of holomorphic vector bundles, general results
Secondary: 32G05: Deformations of complex structures 14F18: Multiplier ideals
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berndtsson, B., Curvature of vector bundles associated to holomorphic fibrations , Ann. of Math. 169 (2009), no. 2, 531–560.Google Scholar
Berndtsson, B. and Păun, M., Bergman kernels and the pseudoeffectivity of relative canonical bundles , Duke Math. J. 145 (2008), no. 2, 341–378.CrossRefGoogle Scholar
Berndtsson, B., Păun, M. and Wang, X., Algebraic fiber spaces and curvature of higher direct images , J. Inst. Math. Jussieu. 21 (2022), 973–1028.CrossRefGoogle Scholar
Błocki, Z., Suita conjecture and the Ohsawa–Takegoshi extension theorem , Invent. Math. 193 (2013), no. 1, 149–158.CrossRefGoogle Scholar
de Cataldo, M. A. A., Singular Hermitian metrics on vector bundles , J. Reine Angew. Math. 502 (1998), 93–122.CrossRefGoogle Scholar
Demailly, J.-P., Estimations ${L}^2$ pour l’opérateur $\overline{\partial}$ d’un fibré vectoriel holomorphe semi-positif au dessus d’une variété Kählérienne complète , Ann. Sci. Ec. Norm. Sup. 15 (1982), 457–511.CrossRefGoogle Scholar
Demailly, J.-P., “Regularization of closed positive currents of type (1,1) by the flow of a Chern connection” in Contributions to Complex Analysis and Analytic Geometry, Aspects of Mathematics, Vol. E26, Vieweg, Braunschweig, 1994, pp. 105–126.Google Scholar
Demailly, J.-P., Analytic Methods in Algebraic Geometry, Surveys of Modern Mathematics, Vol. 1, Higher Education Press, Beijing, 2010.Google Scholar
Demailly, J.-P., Complex Analytic and Differential Geometry, online book at: https://www-fourier.ujf-grenoble.fr/~demailly/manuscripts/agbook.pdf. Institut Fourier, 2012.Google Scholar
Demailly, J.-P. and Skoda, H., Relations Entre les Notions de positivité P.A. Griffiths et de S. Nakano, Lecture Notes in Mathematics, Vol. 822, Springer, Berlin, 1980, pp. 304–309.Google Scholar
Deng, F., Ning, J., Wang, Z. and Zhou, X., Positivity of holomorphic vector bundles in terms of ${L}^p$ -conditions of $\overline{\partial}$ , Math. Ann. (2022), DOI 10.1007/s00208-021-02348-7 Google Scholar
Fornaess, J. E. and Narasimhan, R., The Levi problem on complex spaces with singularities , Math. Ann. 248 (1980), 47–72.CrossRefGoogle Scholar
Guan, Q. and Zhou, X., Optimal constant problem in the ${L}^2$ extension theorem, C. R. Math. Acad. Sci. Paris 350 (15–16) (2012), 753–756.CrossRefGoogle Scholar
Hacon, C., Popa, M. and Schnell, C., “Algebraic Fiber space over abelian varieties: Around a recent theorem by Cao Nad Păun” in Local and Global Methods in Algebraic Geometry, Contemporary Mathematics, Vol. 712, American Mathematical Society, Providence, RI, 2018, pp. 143–195.CrossRefGoogle Scholar
Hartshorne, R., Ample vector bundles, Publ. Math. I.H.E.S. 29 (1966), 63–94.CrossRefGoogle Scholar
Hosono, G. and Inayama, T., A converse of Hörmander’s ${L}^2$ -estimate and new positivity notions for vector bundles , Sci China Math 64 (2021), 1745–1756, DOI 10.1007/s11425-019-1654-9 CrossRefGoogle Scholar
Inayama, T., Nakano positivity of singular Hermitian metrics and vanishing theorems of Demailly–Nadel–Nakano type , Algebraic Geometry 9 (2022), no. 1, 69–92.CrossRefGoogle Scholar
Liu, K., Sun, X. and Yang, X., Positivity and vanishing theorems for ample vector bundles , J. Algebraic Geom. 22 (2013), no. 2, 303–331.CrossRefGoogle Scholar
Lombardi, L. and Schnell, C., Singular Hermitian metrics and the decomposition theorem of Catanese, Fujita, and Kawamata, Proceedings of the American Mathematical Society, 152 (2023), no. 1, 137–146. doi:10.1090/proc/16625 CrossRefGoogle Scholar
Nadel, A. M., Multiplier ideal sheaves and Kähler–Einstein metrics of positive scalar curvature , Proc. Nat. Acad. Sci. U.S.A., 86 (1989), 7299–7300; and Annals of Math. 132 (1990), no. 3, 549–596.CrossRefGoogle ScholarPubMed
Naumann, P., An approach to the Griffiths conjecture , Math. Res. Lett. 28 (2021), no. 5, 1505–1523.CrossRefGoogle Scholar
Ohsawa, T. and Takegoshi, K., On the extension of ${L}^2$ holomorphic functions, Math. Z. 195 (1987), no. 2, 197–204.CrossRefGoogle Scholar
Păun, M. and Takayama, S., Positivity of twisted relative pluricanonical bundles and their direct images , J. Algebraic Geom. 27 (2018), 211–272.CrossRefGoogle Scholar
Raufi, H., Singular hermitian metrics on holomorphic vector bundles , Ark. Mat. 53 (2015), no. 2, 359–382.CrossRefGoogle Scholar
Schumacher, G., “ The curvature of the Petersson–Weil metric on the Moduli space of Kähler–Einstein manifolds ” in Complex Analysis and Geometry, University Series in Mathematics, Plenum, New York, 1993, pp. 339–354.CrossRefGoogle Scholar
Siu, Y.-T., Complex-analyticity of harmonic maps, vanishing and Lefschetz theorems , J. Differ. Geom. 17 (1982), 55–138.CrossRefGoogle Scholar
Umemura, H., Some results in the theory of vector bundles , Nagoya Math. J. 52 (1973), 97–128.CrossRefGoogle Scholar
Watanabe, Y., Nakano–Nadel type, Bogomolov–Sommese type vanishing and singular dual Nakano semi-positivity, accepted for publication in Ann. Fac. Sci. Toulouse Math., arXiv:2209.00823v2, 2022.Google Scholar
Watanabe, Y., Bogomolov–Sommese type vanishing theorem for holomorphic vector bundles equipped with positive singular Hermitian metrics , Math.Z. 303 (2023), DOI 10.1007/s00209-023-03252-3 CrossRefGoogle Scholar
Zou, Y. and Watanabe, Y., On the direct image of the adjoint big and nef line bundles, preprint, arXiv:2401.17684.Google Scholar