Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T08:05:36.749Z Has data issue: false hasContentIssue false
  • English
  • Français

Distortion Theorems in the Theory of Schlicht Functions

Published online by Cambridge University Press:  22 January 2016

Shohei Nagura  and
Yusaku Komatu
Shohei Nagura
Affiliation:
Mathematical Institute, Nagoya University Tokyo Institute of Technology
Yusaku Komatu
Affiliation:
Mathematical Institute, Nagoya University Tokyo Institute of Technology
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 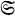be the family of analytic functions F(z) which are regular and schlicht in the circle E: |z| < 1 and normalized at the origin such that F(0) = 0 and F′(0) = 1. Let 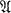be the subfamily of 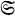consisting of all functions, each of which possesses, as boundary of its image-domain., a closed Jordan curve which is supposed to be regular analytic. Then 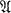is everywhere dense in the original family 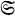. Hence, by an approximation theorem of Carathéodory on the kernel of sequence of domains, we may restrict ourselves within 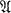, so far as we concern the estimation of continuous functionals on .

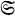Type
Research Article
Information
Nagoya Mathematical Journal , Volume 1 , June 1950 , pp. 25 - 33
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1950

References

1) Schaeffer, A. C. and Spencer, D. C., The coefficients of schlicht functions, II. Duke Math. Journ. 12 (1945), 107–125.CrossRefGoogle Scholar

2) Komatu, Y. and Nagura, S., Theory of schlicht functions. Sûgaku 1 (1948/9), 286–302. (Japanese.)Google Scholar

3) Komatu, Y., Fundamental differential equations in the theory of conformal mapping. Proc. of Japan Acad. Tokyo 25 (1949), 1–10.Google Scholar

4) A proof of the theorem by using Löwner’s equation has been given by Golusin, G. M., Über einige Abschatzungen von Funktionen, welche den Kreis konform und schlicht abbilden. Recueil Math. 36 (1929), 152–172. (in Russian.)Google Scholar

5) A proof by the method of Löwner’s equation has been given by Golusin, G. M., Über die Verzerrungssätze der schlichten konformen Abbildungen. Recueil Math. 1 (43) (1936), 127–135. (in Russian.)Google Scholar

6) Golusin, G. M., Ergänzung zur Arbeit “Über die Verzerrungssätze der schlichten konformen Abbildungen.” Recueil Math. 2 (44) (1937), 685–688. (in Russian.)Google Scholar

7) Grunsky, H., Neue Abschätzungen zur konformen Abbildung ein- und mehriach zusammenhängender Bereiche. Schriften math. Sem. u. Inst. angew. Math. Univ. Berlin 1 (1932/3), 95–140.Google Scholar

8) G. M. Golusin, loc. cit. 5) and Sur les théorèmes de rotation dans la théorie des fonctions univalentes. Recueil Math. 1(43) (1936), 293-296.

9) Basilewitsch, J., Sur les théorèmes de Koebe-Bieberbach. Recueil Math. 1 (43) (1936), 283–292.Google Scholar

10) See loc. cit.3)

12) Komatu, Cf. Y., Untersuchungen über konformen Abbildung von zweifach zusammen-hängenden Gebieten. Proc. Phys.-Math. Soc. 25 (1943), 1–42 Google Scholar, where the concrete expressions for various quantities, especially for extremal functions, are also given.

13) Cf. loc. cit. 12), p. 26 et seq.

14) Cf. also loc. cit. 12).