Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-12T05:39:39.803Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirichletsche Abbildungen

Published online by Cambridge University Press:  22 January 2016

C. Constantinescu
C. Constantinescu*
Affiliation:
Mathematisches Institut, der Rumänischen Akademie
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Für jede Riemannsche Fläche R bezeichnen wir mit M(R) die Algebra von Royden auf R und mit R* (bzw. ΔR)- die Kompaktifizierung (bzw. den idealen Rand) von Royden von R ([5]). Für jede Funktion ξ ∊ M(R) sei Jξ das kompakte Segment 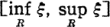und X(R) der kompakte Raum 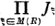. Laut der Definition von R* ist jede Funktion ξ∊M(R) auf R* (in eindeutiger Weise) stetig fortsetzbar. Bezeichnet man ebenfalls mit ξ die so fortgesetzte Funktion und mit φR die Abbildung 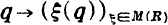von R*→X(R), so ist φR ein Homeomorphismus von R* auf φR(R*).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 20 , June 1962 , pp. 75 - 89
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1962

References

Literatur

[1] Constantinescu, C. und Cornea, A.: Über den idealen Rand und einige seiner Anwendungen bei der Klassifikation der Riemannschen Flächen, Nagoya Math. Journ., 13 (1958), 169–233.Google Scholar
[2] Constantinescu, C. und Cornea, A.: Über das Verhalten der analytischen Abbildungen Riemannscher Flächen auf dem idealen Rand von Martin, Nagoya Math. Journ., 17 (1960), 1–87.CrossRefGoogle Scholar
[3] Heins, M.: On the Lindeiöf principle, Ann. of Math., 61 (1955), 440–473.Google Scholar
[4] Kusunoki, Y. and Mori, S.: On the harmonic boundary of an open Riemann surface, Japan. Journ. Math., 29 (1959), 52–56.Google Scholar
[5] Nakai, M.: A measure on the harmonic boundary of a Riemann surface, Nagoya Math. Journ., 17 (1960), 181–218.Google Scholar