Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Holopainen, Ilkka
Lang, Urs
and
Vähäkangas, Aleksi
2007.
Dirichlet problem at infinity on Gromov hyperbolic metric measure spaces.
Mathematische Annalen,
Vol. 339,
Issue. 1,
p.
101.


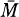 =
=