Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T15:39:12.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension and lower central subgroups of metabelian p-groups

Published online by Cambridge University Press:  22 January 2016

Narain Gupta  and
Ken-Ichi Tahara
Narain Gupta
Affiliation:
Department of Mathematics University of Manitoba Winnipeg, R3T 2N2, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is a well-known result due to Sjogren [9] that if G is a finitely generated p-group then, for all n ≦ − 1, the (n + 2)-th dimension sub-group Dn+2(G) of G coincides with γn+2(G), the (n + 2)-th term of the lower central series of G. This was earlier proved by Moran [5] for n ≦ p − 2. For p = 2, Sjogren’s result is the best possible as Rips [8] has exhibited a finite 2-group G for which D4G) ≠ γ4(G) (see also Tahara [10, 11]). In this note we prove that if G is a finitely generated metabelian p-group then, for all 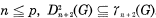. It follows, in particular, that, for p odd, 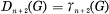for all n ≦ p and all metabelian p-groups G.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 100 , December 1985 , pp. 127 - 133
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1985

References

[ 1 ] Gupta, N., On the dimension subgroups of metabelian groups, J. Pure Appl. Algebra, 24 (1982), 1–6.Google Scholar
[ 2 ] Gupta, N., Sjogren’s Theorem for dimension subgroups—The metabelian case, Annals of Math. Study (1985), to appear.Google Scholar
[ 3 ] Losey, G., N-series and nitration of the augmentation ideal, Canad. J. Math., 26 (1974), 962–977.Google Scholar
[ 4 ] Magnus, W., Karrass, A. and Solitar, D., Combinatorial Group Theory, Interscience, New York, 1966.Google Scholar
[ 5 ] Moran, S., Dimension subgroups modn, Proc. Camb. Phil. Soc, 68 (1970), 579–582.Google Scholar
[ 6 ] Passi, I.B.S., Dimension subgroups, J. Algebra, 9 (1968), 152–182.Google Scholar
[ 7 ] Passi, I.B.S., Group Rings and Their Augmentation Ideals, Springer Lecture Notes in Math., 715 (1979), Springer-Verlag, Berlin-Heidelberg-New York.Google Scholar
[ 8 ] Rips, E., On the fourth integer dimension subgroup, Israel J. Math., 12 (1972), 342–346.Google Scholar
[ 9 ] Sjogren, J. A., Dimension and lower central subgroups, J. Pure Appl. Algebra, 14 (1979), 175–194.Google Scholar
[10] Tahara, K., On the structure of Qs(G) and the fourth dimension subgroup, Japan. J. Math. (New Ser.), 3 (1977), 381–394.Google Scholar
[11] Tahara, K., The fourth dimension subgroups and polynomial maps, II, Nagoya Math. J., 69 (1978), 1–7.CrossRefGoogle Scholar