Article contents
Differential operators on a hypersurface
Published online by Cambridge University Press: 22 January 2016
Extract
We study differential operators on an affine algebraic variety, especially a hypersurface, in the context of Nakai’s Conjecture. We work over a field k of characteristic zero. Let X be a reduced affine algebraic variety over k and let A be its coordinate ring. Let 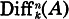 be the A-module of differential operators of A over k of order ≤ n. Nakai’s Conjecture asserts that if
be the A-module of differential operators of A over k of order ≤ n. Nakai’s Conjecture asserts that if 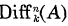 is generated by
is generated by 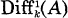 for every n ≥ 2 then A is regular. In 1973 Mount and Villamayor [6] proved this in the case when X is an irreducible curve. In the general case no progress seems to have been made on the conjecture, except for a result of Brown [2], where the assertion is proved under an additional hypothesis. An interesting result proved by Becker [1] and Rego [8] says that Nakai’s Conjecture implies the Conjecture of Zariski-Lipman, which is still open in the general case and which asserts that if the module of k-derivations of A is A-projective then A is regular.
for every n ≥ 2 then A is regular. In 1973 Mount and Villamayor [6] proved this in the case when X is an irreducible curve. In the general case no progress seems to have been made on the conjecture, except for a result of Brown [2], where the assertion is proved under an additional hypothesis. An interesting result proved by Becker [1] and Rego [8] says that Nakai’s Conjecture implies the Conjecture of Zariski-Lipman, which is still open in the general case and which asserts that if the module of k-derivations of A is A-projective then A is regular.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1986
References
- 7
- Cited by


