Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-14T10:43:08.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Derivations on white noise functionals

Published online by Cambridge University Press:  22 January 2016

Nobuaki Obata
Nobuaki Obata*
Affiliation:
Graduate School of Polymathematics, Nagoya University, Nagoya, 464-01Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Gaussian space (E*, μ) is a natural infinite dimensional analogue of Euclidean space with Lebesgue measure and a special choice of a Gelfand triple 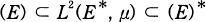gives a fundamental framework of white noise calculus [2] as distribution theory on Gaussian space. It is proved in Kubo-Takenaka [7] that (E) is a topological algebra under pointwise multiplication. The main purpose of this paper is to answer the fundamental question: what are the derivations on the algebra (E)?

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 139 , September 1995 , pp. 21 - 36
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Albeverio, S., Hida, T., Potthoff, J., Röckner, M. and Streit, L., Dirichlet forms in terms of white noise analysis II. Closability and diffusion processes, Rev. Math. Phys., 1 (1990), 313–323.Google Scholar
[ 2 ] Hida, T., “Analysis of Brownian Functionals,” Carleton Math. Lect. Notes no. 13, Carleton University, Ottawa, 1975.Google Scholar
[ 3 ] Hida, T., Kuo, H.-H. and Obata, N., Transformations for white noise functionals, J. Funct. Anal., 111 (1993), 259–277.Google Scholar
[ 4 ] Hida, T., Obata, N. and Saitô, K., Infinite dimensional rotations and Laplacians in terms of white noise calculus, Nagoya Math. J., 128 (1992), 65–93.Google Scholar
[ 5 ] Hida, T., Potthoff, J. and Streit, L., Dirichlet forms and white noise analysis, Commun. Math. Phys., 116 (1988), 235–245.Google Scholar
[ 6 ] Ikeda, N. and Watanabe, S., “Stochastic Differential Equations and Diffusion Processes (2nd ed.),” North-Holland, Amsterdam/New York, 1988.Google Scholar
[ 7 ] Kubo, I. and Takenaka, S., Calculus on Gaussian white noise I-IV, Proc. Japan Acad., 56A (1980), 376–380; 411–416; 57A (1981), 433–437; 58A (1982), 186–189.Google Scholar
[ 8 ] Kubo, I. and Yokoi, Y., A remark on the space of testing random variables in the white noise calculus, Nagoya Math. J., 115 (1989), 139–149.Google Scholar
[ 9 ] Kuo, H.-H., On Laplacian operators of generalized Brownian functionals, in “Stochastic Processes and Their Applications (T. Hida and K. Itô, eds.),” Lect. Notes in Math. Vol. 1203, Springer-Verlag, 1986, pp. 119–128.Google Scholar
[10] Meyer, P. A., “Quantum Probability for Probabilists,” Lect. Notes in Math. Vol. 1538, Springer-Verlag, 1993.Google Scholar
[11] Obata, N., Rotation-invariant operators on white noise functionals, Math. Z., 210 (1992), 69–89.Google Scholar
[12] Obata, N., An analytic characterization of symbols of operators on white noise functionals, J. Math. Soc. Japan, 45 (1993), 421–445.Google Scholar
[13] Obata, N., Operator calculus on vector-valued white noise functionals, J. Funct. Anal., 121 (1994), 185–232.Google Scholar
[14] Obata, N., “White Noise Calculus and Fock Space,” Lect. Notes in Math. Vol. 1577, Springer-Verlag, 1994.Google Scholar
[15] Parthasarathy, K. R., “An Introduction to Quantum Stochastic Calculus,” Birkhäuser, 1992.Google Scholar