Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T14:58:41.059Z Has data issue: false hasContentIssue false
  • English
  • Français

de Rham cohomology of local cohomology modules: The graded case

Part of: Commutative algebra: Homological methods Differential algebra

Published online by Cambridge University Press:  11 January 2016

Tony J. Puthenpurakal
Tony J. Puthenpurakal*
Affiliation:
Department of Mathematics, Indian Institute of Technology, Bombay Powai, Mumbai 400 076, India, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a field of characteristic zero, and let R = K[X1,… ,Xn]. Let An(K) = K⟨X1,… ,Xn,∂1,… ,∂n⟩ be the nth Weyl algebra over K. We consider the case when R and An(K) are graded by giving deg Xi = ωi and deg ∂i = –ωi for i = 1,…,n (here ωi are positive integers). Set 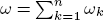. Let I be a graded ideal in R. By a result due to Lyubeznik the local cohomology modules 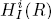are holonomic (An(K))-modules for each i≥0. In this article we prove that the de Rham cohomology modules 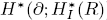are concentrated in degree —ω; that is, 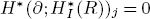for j ≠ –ω. As an application when A = R/(f) is an isolated singularity, we relate 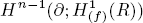to Hn-1(∂(f);A), the (n – 1)th Koszul cohomology of A with respect to ∂1(f),…, ∂n(f).

MSC classification

Secondary: 13D45: Local cohomology 13N10: Rings of differential operators and their modules
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 217 , March 2015 , pp. 1 - 21
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2015

References

[1] Björk, J.-E., Rings of Differential Operators, North-Holland Math. Library 21, North-Holland, Amsterdam, 1979. MR 0549189.Google Scholar
[2] Bruns, W. and Herzog, J., Cohen-Macaulay Rings, Cambridge Stud. Adv. Math. 39, Cambridge University Press, Cambridge, 1993. MR 1251956.Google Scholar
[3] Lyubeznik, G., Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra), Invent. Math. 113 (1993), 41–55. MR 1223223. DOI 10.1007/BF01244301.CrossRefGoogle Scholar
[4] Ma, L. and Zhang, W., Eulerian graded 𝒟-modules, Math. Res. Lett. 21 (2014), 149–167. MR 3247047. DOI 10.4310/MRL.2014.v21.n1.a13.CrossRefGoogle Scholar
[5] Puthenpurakal, T. J., De Rham cohomology of local cohomology modules, preprint, arXiv:1302.0116v2 [math.AC].Google Scholar
[6] Puthenpurakal, T. J. and Reddy, R. B. T., de Rham cohomology of , where V(f) is a smooth hypersurface in ℙn, preprint, arXiv: 1310.4654v1 [math.AC].Google Scholar