Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ikoma, Kazuo
1965.
On the Distortion and Correspondence under Quasiconformal Mappings in Space.
Nagoya Mathematical Journal,
Vol. 25,
Issue. ,
p.
175.


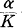 -dimensional measure zero in a Jordan domain
-dimensional measure zero in a Jordan domain 