Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-04T20:09:11.233Z Has data issue: false hasContentIssue false
  • English
  • Français

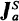Countable -admissible Ordinals

Published online by Cambridge University Press:  22 January 2016

Juichi Shinoda
Juichi Shinoda*
Affiliation:
Department of Mathematics, College of General Education, Nagoya University, Chikusa-ku, Nagoya 464, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [3], Platek constructs a hierarchy of jumps 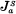indexed by elements a of a set 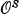of ordinal notations. He asserts that a real X ⊆ ω is recursive in the superjump S if and only if it is recursive in some 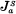. Unfortunately, his assertion is not correct as is shown in [1]. In [1], it also has been shown that an ordinal > ω is 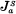-admissible if it is |a|S-recursively inaccessible, where |a|s- is the ordinal denoted by a.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 99 , September 1985 , pp. 1 - 10
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1985

References

[ 1 ] Aczel, P. and Hinman, P. G., Recursion in the super jump, in: Generalized Recursion Theory, edited by Fenstad, J. E. and Hinman, P. G. (North-Holland, Amsterdam, 1974), 3–41.Google Scholar
[ 2 ] Barwise, J., Admissible Sets and Structures, Springer, Berlin, 1975.Google Scholar
[ 3 ] Platek, R., A countable hierarchy for the superjump, in : Logic Colloquium ’69, edited by Gandy, R. O. and Yates, C. E. M. (North-Holland, Amsterdam, 1971), 257–271.Google Scholar
[ 4 ] Sacks, G. E., Countable admissible ordinals and hyperdegrees, Adv. in Math., 19 (1976), 213–262.Google Scholar
[ 5 ] Shinoda, J., On the upper semi-lattice of -degrees, Nagoya Math. J., 80 (1980), 75–106.Google Scholar