Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T23:05:39.606Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPOSITION OPERATORS ON WIENER AMALGAM SPACES

Part of: Harmonic analysis in several variables Nonlinear operators and their properties

Published online by Cambridge University Press:  08 March 2019

DIVYANG G. BHIMANI
DIVYANG G. BHIMANI*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a complex function 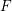$F$ on 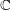$\mathbb{C}$, we study the associated composition operator 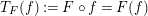$T_{F}(f):=F\circ f=F(f)$ on Wiener amalgam 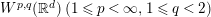$W^{p,q}(\mathbb{R}^{d})\;(1\leqslant p<\infty ,1\leqslant q<2)$. We have shown 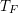$T_{F}$ maps 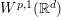$W^{p,1}(\mathbb{R}^{d})$ to 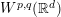$W^{p,q}(\mathbb{R}^{d})$ if and only if 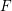$F$ is real analytic on 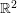$\mathbb{R}^{2}$ and 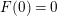$F(0)=0$. Similar result is proved in the case of modulation spaces 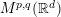$M^{p,q}(\mathbb{R}^{d})$. In particular, this gives an affirmative answer to the open question proposed in Bhimani and Ratnakumar (J. Funct. Anal. 270(2) (2016), 621–648).

MSC classification

Primary: 42B35: Function spaces arising in harmonic analysis 47H30: Particular nonlinear operators (superposition, Hammerstein, Nemytskiĭ, Uryson, etc.) 42B37: Harmonic analysis and PDE
Type
Article
Information
Nagoya Mathematical Journal , Volume 240 , December 2020 , pp. 257 - 274
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bényi, Á., Gröchenig, K., Okoudjou, K. A. and Rogers, L. G., Unimodular Fourier multipliers for modulation spaces, J. Funct. Anal. 246(2) (2007), 366–384.10.1016/j.jfa.2006.12.019Google Scholar
Bényi, Á. and Oh, T., Modulation spaces, Wiener amalgam spaces, and Brownian motions, Adv. Math. 228(5) (2011), 2943–2981.10.1016/j.aim.2011.07.023Google Scholar
Bényi, Á. and Okoudjou, K. A., Local well-posedness of nonlinear dispersive equations on modulation spaces, Bull. Lond. Math. Soc. 41(3) (2009), 549–558.10.1112/blms/bdp027Google Scholar
Bhimani, D. G., Contraction of functions in modulation spaces, Integral Transforms Spec. Funct. 26(9) (2015), 678–686.10.1080/10652469.2015.1036055Google Scholar
Bhimani, D. G., The Cauchy problem for the Hartree type equation in modulation spaces, Nonlinear Anal. 130 (2016), 190–201.10.1016/j.na.2015.10.002Google Scholar
Bhimani, D. G. and Ratnakumar, P. K., Functions operating on modulation spaces and nonlinear dispersive equations, J. Funct. Anal. 270(2) (2016), 621–648.10.1016/j.jfa.2015.10.017Google Scholar
Bourdaud, G. and Sickel, W., “Composition operators on function spaces with fractional order of smoothness, harmonic analysis and nonlinear partial differential equations”, in RIMS Kokyuroku Bessatsu B26, Res. Inst. Math. Sci. (RIMS), Kyoto, 2011, 93–132.Google Scholar
Cordero, E. and Nicola, F., Remarks on Fourier multipliers and applications to wave equation, J. Math. Anal. Appl. 353 (2009), 583–591.10.1016/j.jmaa.2008.12.027Google Scholar
Cunanan, J. and Sugimoto, M., Unimodular Fourier multipliers on Wiener amalgam spaces, J. Math. Anal. Appl. 419(2) (2014), 738–747.10.1016/j.jmaa.2014.05.001Google Scholar
Feichtinger, H. G., Modulation spaces on locally compact abelian groups, Technical report, University of Vienna, 1983.Google Scholar
Folland, G. B., “Real analysis”, in Modern Techniques and Their Applications, Wiley-Interscience Publ., New York, 1999.Google Scholar
Gröchenig, K., Foundations of Time-Frequency Analysis, Birkhäuser Boston, Inc., Boston, MA, 2001.10.1007/978-1-4612-0003-1Google Scholar
Helson, H., Kahane, J.-P., Katznelson, Y. and Rudin, W., The functions which operate on Fourier transforms, Acta Math. 102 (1959), 135–157.10.1007/BF02559571Google Scholar
Kato, T., Sugimoto, M. and Tomita, N., Nonlinear operations on a class of modulation spaces, preprint, 2018, arXiv:1801.06803.Google Scholar
Kobayshi, M. and Sato, E., Operating functions on modulation and Wiener amalgam spaces, Nagoya Math. J. 270 (2018), 72–82.10.1017/nmj.2017.3Google Scholar
Lévy, P., Sur la convergence absolue des séries de Fourier, Compos. Math. 1 (1934), 1–14.Google Scholar
Okoudjou, K., A Beurling–Helson type theorem for modulation spaces, J. Funct. Spaces Appl. 7(1) (2009), 33–41.10.1155/2009/956891Google Scholar
Reich, M., Reissig, M. and Sickel, W., Non-analytic superposition results on modulation spaces with subexponential weights, J. Pseudo-Differ. Oper. Appl. 7(3) (2016), 365–409.10.1007/s11868-016-0148-xGoogle Scholar
Rudin, W., A strong converse of the Wiener–Levy theorem, Canad. J. Math. 14 (1962), 694–701.10.4153/CJM-1962-059-3Google Scholar
Rudin, W., Fourier Analysis on Groups, John Wiley & Sons, Inc., Wiley Classics Library Edition 1990.10.1002/9781118165621Google Scholar
Ruzhansky, M., Sugimoto, M., Toft, J. and Tomita, N., Changes of variables in modulation and Wiener amalgam spaces, Math. Nachr. 284(16) (2011), 2078–2092.10.1002/mana.200910199Google Scholar
Sugimoto, M. and Tomita, N., The dilation property of modulation spaces and their inclusion relation with Besov spaces, J. Funct. Anal. 248(1) (2007), 79–106.10.1016/j.jfa.2007.03.015Google Scholar
Sugimoto, M., Tomita, N. and Wang, B., Remarks on nonlinear operations on modulation spaces, Integral Transforms Spec. Funct. 22(4–5) (2011), 351–358.10.1080/10652469.2010.541054Google Scholar
Ruzhansky, M., Sugimoto, M. and Wang, B., “Modulation spaces and nonlinear evolution equations”, in Evolution Equations of Hyperbolic and Schrödinger Type, Progr. Math. 301, Birkhäuser/Springer Basel AG, Basel, 2012, 267–283.10.1007/978-3-0348-0454-7_14Google Scholar
Triebel, H., Modulation spaces on the Euclidean n-space, Z. Anal. Anwend. 2(5) (1983), 443–457.10.4171/ZAA/79Google Scholar
Wang, B., Lifeng, Z. and Boling, G., Isometric decomposition operators, function spaces E p, q𝜆 and applications to nonlinear evolution equations, J. Funct. Anal. 233(1) (2006), 1–39.Google Scholar
Wang, B., Zhaohui, H., Chengchun, H. and Zihua, G., Harmonic Analysis Method for Nonlinear Evolution Equations. I, World Scientific Publishing Co. Pte. Lt., Singapore, 2011.10.1142/8209Google Scholar
Wiener, N., Tauberian theorems, Ann. of Math. (2) 33 (1932), 1–100.10.2307/1968102Google Scholar