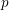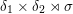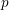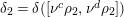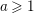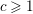1 Introduction
Let us denote by
![]() $G_{n}$
either symplectic or odd special orthogonal group of rank
$G_{n}$
either symplectic or odd special orthogonal group of rank
![]() $n$
over a nonarchimedean local field
$n$
over a nonarchimedean local field
![]() $F$
of characteristic different than two.
$F$
of characteristic different than two.
According to the Langlands classification, every irreducible admissible representation of
![]() $G_{n}$
can be obtained as an irreducible subrepresentation of the induced representation of the form
$G_{n}$
can be obtained as an irreducible subrepresentation of the induced representation of the form
where
![]() $\unicode[STIX]{x1D70F}$
is a tempered representation of some
$\unicode[STIX]{x1D70F}$
is a tempered representation of some
![]() $G_{n^{\prime }}$
, while
$G_{n^{\prime }}$
, while
![]() $\unicode[STIX]{x1D6FF}_{i}$
is an irreducible essentially square-integrable representation of
$\unicode[STIX]{x1D6FF}_{i}$
is an irreducible essentially square-integrable representation of
![]() $\text{GL}(n_{i},F)$
, for
$\text{GL}(n_{i},F)$
, for
![]() $i=1,2,\ldots ,k$
, subject to certain constraints on the central exponents of representations
$i=1,2,\ldots ,k$
, subject to certain constraints on the central exponents of representations
![]() $\unicode[STIX]{x1D6FF}_{i}$
(we refer the reader to Section 2, where this is discussed in more detail for the groups under consideration). By the results of [Reference Zelevinsky17],
$\unicode[STIX]{x1D6FF}_{i}$
(we refer the reader to Section 2, where this is discussed in more detail for the groups under consideration). By the results of [Reference Zelevinsky17],
![]() $\unicode[STIX]{x1D6FF}_{i}$
is of the form
$\unicode[STIX]{x1D6FF}_{i}$
is of the form
for
![]() $a_{i},b_{i}\in \mathbb{R}$
be such that
$a_{i},b_{i}\in \mathbb{R}$
be such that
![]() $b_{i}-a_{i}\in \mathbb{Z}$
, and an irreducible cuspidal representation
$b_{i}-a_{i}\in \mathbb{Z}$
, and an irreducible cuspidal representation
![]() $\unicode[STIX]{x1D70C}_{i}$
of
$\unicode[STIX]{x1D70C}_{i}$
of
![]() $\text{GL}(n_{\unicode[STIX]{x1D70C}_{i}},F)$
.
$\text{GL}(n_{\unicode[STIX]{x1D70C}_{i}},F)$
.
It follows from a result of Harish-Chandra (as in [Reference Waldspurger16, Proposition III.4.1]) that a tempered representation of
![]() $G_{n^{\prime }}$
embeds in an induced representation of the form
$G_{n^{\prime }}$
embeds in an induced representation of the form
![]() $\unicode[STIX]{x1D6FF}_{1}\times \cdots \times \unicode[STIX]{x1D6FF}_{k^{\prime }}\rtimes \unicode[STIX]{x1D70E}$
, where
$\unicode[STIX]{x1D6FF}_{1}\times \cdots \times \unicode[STIX]{x1D6FF}_{k^{\prime }}\rtimes \unicode[STIX]{x1D70E}$
, where
![]() $\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{k^{\prime }}$
are irreducible essentially square-integrable representations of general linear groups, and
$\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{k^{\prime }}$
are irreducible essentially square-integrable representations of general linear groups, and
![]() $\unicode[STIX]{x1D70E}$
is an irreducible square-integrable representation of
$\unicode[STIX]{x1D70E}$
is an irreducible square-integrable representation of
![]() $G_{n^{\prime \prime }}$
,
$G_{n^{\prime \prime }}$
,
![]() $n^{\prime \prime }\leqslant n^{\prime }$
. Combining this result with the Langlands classification and more recent classification of the square-integrable unitary duals of classical groups over nonarchimedean local fields, given in [Reference Mœglin and Tadić12], one can deduce that every irreducible admissible representation of
$n^{\prime \prime }\leqslant n^{\prime }$
. Combining this result with the Langlands classification and more recent classification of the square-integrable unitary duals of classical groups over nonarchimedean local fields, given in [Reference Mœglin and Tadić12], one can deduce that every irreducible admissible representation of
![]() $G_{n}$
can be obtained as an irreducible subquotient of the induced representation of the form
$G_{n}$
can be obtained as an irreducible subquotient of the induced representation of the form
for irreducible essentially square-integrable representations
![]() $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k^{\prime \prime }}$
of general linear groups and a strongly positive discrete series
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k^{\prime \prime }}$
of general linear groups and a strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}_{sp}$
of
$\unicode[STIX]{x1D70E}_{sp}$
of
![]() $G_{n^{\prime \prime \prime }}$
for some
$G_{n^{\prime \prime \prime }}$
for some
![]() $n^{\prime \prime \prime }\leqslant n$
.
$n^{\prime \prime \prime }\leqslant n$
.
Consequently, strongly positive representations can be observed as the basic building blocks in known construction of the nonunitary duals of classical groups over nonarchimedean local fields, and it is of particular interest to obtain deeper insight into the explicit description of the composition series of representations of the form (1). We note that an algebraic classification of strongly positive discrete series of metaplectic groups, which also holds in the case of classical groups, is given in [Reference Matić4], and some further properties of strongly positive representations have been studied in [Reference Matić5], [Reference Matić6] and [Reference Matić and Tadić10].
Composition factors of the generalized principal series
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
have been completely determined by Muić in [Reference Muić13], in terms of the Mœglin–Tadić classification of discrete series. This classification relies on the Basic assumption, which now follows from the recent work of Arthur [Reference Arthur1] and [Reference Mœglin11, Théorème 3.1.1] (for more details on the Basic Assumption, we refer the reader to [Reference Mœglin and Tadić12, Section
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
have been completely determined by Muić in [Reference Muić13], in terms of the Mœglin–Tadić classification of discrete series. This classification relies on the Basic assumption, which now follows from the recent work of Arthur [Reference Arthur1] and [Reference Mœglin11, Théorème 3.1.1] (for more details on the Basic Assumption, we refer the reader to [Reference Mœglin and Tadić12, Section
![]() $2$
]). There are three essentially different cases which appear in [Reference Muić13], and each of them has to be studied separately:
$2$
]). There are three essentially different cases which appear in [Reference Muić13], and each of them has to be studied separately:
![]() $a\geqslant 1$
,
$a\geqslant 1$
,
![]() $a\leqslant 0$
and
$a\leqslant 0$
and
![]() $a=\frac{1}{2}$
.
$a=\frac{1}{2}$
.
In this paper, we go one step further by giving an explicit description of the composition factors of the induced representation of the form
where
![]() $a\geqslant 1,c\geqslant 1$
, and
$a\geqslant 1,c\geqslant 1$
, and
![]() $\unicode[STIX]{x1D70E}_{sp}$
is a strongly positive discrete series. An advantage of the considered case is that every tempered subquotient of the induced representation (2) is strongly positive, and our description presents a natural continuation of the problem considered in [Reference Muić13].
$\unicode[STIX]{x1D70E}_{sp}$
is a strongly positive discrete series. An advantage of the considered case is that every tempered subquotient of the induced representation (2) is strongly positive, and our description presents a natural continuation of the problem considered in [Reference Muić13].
We note that it is a direct consequence of the results of [Reference Muić13] and [Reference Matić9, Proposition 3.2], that the representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
is multiplicity one, and can be of length one, two, three or four. On the other hand, our results show that the induced representation (2) is again multiplicity one, and can be of length one to eight, but not of length five.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
is multiplicity one, and can be of length one, two, three or four. On the other hand, our results show that the induced representation (2) is again multiplicity one, and can be of length one to eight, but not of length five.
The main role in our determination is played by the necessary and sufficient conditions under which the induced representation of the form (2) contains a strongly positive subquotient, which are given in [Reference Matić7] and based on the description of Jacquet modules of discrete series of particular type, given in [Reference Matić8]. Those results enable us to obtain candidates for irreducible subquotients of the induced representation (2), calculating various Jacquet modules of such induced representation. To determine whether an obtained irreducible representation is contained in the composition series of (2), we use sometimes rather involved arguments based on the combination of the intertwining operators method and the Jacquet modules method.
Let us describe the contents of the paper in more detail.
Section 2 provides in details the main notation and ingredients needed in this work. In Section 3, we recall some known results, which are used in the paper. Also, in that section we prove some technical results which enable us to determine all possible irreducible subquotients of the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Detailed analysis of the composition factors of the representation
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Detailed analysis of the composition factors of the representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
in the case when
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
in the case when
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])$
is irreducible is provided in Section 4. Description of the composition factors in the remaining case is given in Section 5.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])$
is irreducible is provided in Section 4. Description of the composition factors in the remaining case is given in Section 5.
2 Preliminaries
Let
![]() $F$
denote a nonarchimedean local field of characteristic different than two. The groups we are considering are of the following form: we have a tower of symplectic or (full) orthogonal groups
$F$
denote a nonarchimedean local field of characteristic different than two. The groups we are considering are of the following form: we have a tower of symplectic or (full) orthogonal groups
![]() $G_{n}=G(V_{n})$
, which are the groups of isometries of
$G_{n}=G(V_{n})$
, which are the groups of isometries of
![]() $F$
-vector spaces
$F$
-vector spaces
![]() $V_{n}$
endowed with the nondegenerate form which is skew-symmetric if the tower is symplectic and symmetric otherwise. Here
$V_{n}$
endowed with the nondegenerate form which is skew-symmetric if the tower is symplectic and symmetric otherwise. Here
![]() $n$
stands for the split rank of the group
$n$
stands for the split rank of the group
![]() $G_{n}$
,
$G_{n}$
,
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
The set of standard parabolic subgroups is fixed in a usual way, that is, we fix a minimal
![]() $F$
-parabolic subgroup in
$F$
-parabolic subgroup in
![]() $G_{n}$
consisting of upper-triangular matrixes in the usual matrix realization of the classical group. Then the Levi factors of standard parabolic subgroups have the form
$G_{n}$
consisting of upper-triangular matrixes in the usual matrix realization of the classical group. Then the Levi factors of standard parabolic subgroups have the form
![]() $M=\text{GL}(n_{1},F)\times \cdots \times \text{GL}(n_{k},F)\times G_{n^{\prime }}$
, where
$M=\text{GL}(n_{1},F)\times \cdots \times \text{GL}(n_{k},F)\times G_{n^{\prime }}$
, where
![]() $\text{GL}(m,F)$
denotes a general linear group of rank
$\text{GL}(m,F)$
denotes a general linear group of rank
![]() $m$
over
$m$
over
![]() $F$
. If
$F$
. If
![]() $\unicode[STIX]{x1D6FF}_{i},i=1,2,\ldots ,k$
, is a representation of
$\unicode[STIX]{x1D6FF}_{i},i=1,2,\ldots ,k$
, is a representation of
![]() $\text{GL}(n_{i},F)$
and if
$\text{GL}(n_{i},F)$
and if
![]() $\unicode[STIX]{x1D70F}$
a representation of
$\unicode[STIX]{x1D70F}$
a representation of
![]() $G_{m}$
, then by
$G_{m}$
, then by
![]() $\unicode[STIX]{x1D6FF}_{1}\times \cdots \times \unicode[STIX]{x1D6FF}_{k}\rtimes \unicode[STIX]{x1D70F}$
we denote a normalized parabolically induced representation of the group
$\unicode[STIX]{x1D6FF}_{1}\times \cdots \times \unicode[STIX]{x1D6FF}_{k}\rtimes \unicode[STIX]{x1D70F}$
we denote a normalized parabolically induced representation of the group
![]() $G_{n}$
, induced from the representation by
$G_{n}$
, induced from the representation by
![]() $\unicode[STIX]{x1D6FF}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D6FF}_{k}\otimes \unicode[STIX]{x1D70F}$
of the standard parabolic subgroup with the Levi subgroup equal to
$\unicode[STIX]{x1D6FF}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D6FF}_{k}\otimes \unicode[STIX]{x1D70F}$
of the standard parabolic subgroup with the Levi subgroup equal to
![]() $\text{GL}(n_{1},F)\times \cdots \times \text{GL}(n_{k},F)\times G_{m}$
. Here
$\text{GL}(n_{1},F)\times \cdots \times \text{GL}(n_{k},F)\times G_{m}$
. Here
![]() $n$
equals
$n$
equals
![]() $n_{1}+n_{2}+\cdots +n_{k}+m$
.
$n_{1}+n_{2}+\cdots +n_{k}+m$
.
We denote by
![]() $\text{Irr}(\text{GL}(n,F))$
the set of all irreducible admissible representations of
$\text{Irr}(\text{GL}(n,F))$
the set of all irreducible admissible representations of
![]() $\text{GL}(n,F)$
, and by
$\text{GL}(n,F)$
, and by
![]() $\text{Irr}(G_{n})$
we denote the set of all irreducible admissible representations of
$\text{Irr}(G_{n})$
we denote the set of all irreducible admissible representations of
![]() $G_{n}$
. Let
$G_{n}$
. Let
![]() $R(\text{GL}(n,F))$
denote the Grothendieck group of admissible representations of finite length of
$R(\text{GL}(n,F))$
denote the Grothendieck group of admissible representations of finite length of
![]() $\text{GL}(n,F)$
and define
$\text{GL}(n,F)$
and define
![]() $R(\text{GL})=\oplus _{n\geqslant 0}R(\text{GL}(n,F))$
. Similarly, let
$R(\text{GL})=\oplus _{n\geqslant 0}R(\text{GL}(n,F))$
. Similarly, let
![]() $R(G_{n})$
stand for the Grothendieck group of admissible representations of finite length of
$R(G_{n})$
stand for the Grothendieck group of admissible representations of finite length of
![]() $G_{n}$
and define
$G_{n}$
and define
![]() $R(G)=\oplus _{n\geqslant 0}R(G_{n})$
.
$R(G)=\oplus _{n\geqslant 0}R(G_{n})$
.
We denote by
![]() $\unicode[STIX]{x1D708}$
a composition of the determinant mapping with the normalized absolute value on
$\unicode[STIX]{x1D708}$
a composition of the determinant mapping with the normalized absolute value on
![]() $F$
. Let
$F$
. Let
![]() $\unicode[STIX]{x1D70C}$
denote an irreducible cuspidal representation of
$\unicode[STIX]{x1D70C}$
denote an irreducible cuspidal representation of
![]() $\text{GL}(k,F)$
. By a segment of cuspidal representations, which we denote by
$\text{GL}(k,F)$
. By a segment of cuspidal representations, which we denote by
![]() $[\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}]$
, we mean the set
$[\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}]$
, we mean the set
![]() $\{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}\unicode[STIX]{x1D70C},\ldots ,\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}\}$
. To each such segment we attach an irreducible essentially square-integrable representation
$\{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}\unicode[STIX]{x1D70C},\ldots ,\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}\}$
. To each such segment we attach an irreducible essentially square-integrable representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}])$
of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}])$
of
![]() $\text{GL}(m\cdot k,F)$
, which is a unique irreducible subrepresentation of
$\text{GL}(m\cdot k,F)$
, which is a unique irreducible subrepresentation of
![]() $\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}\times \cdots \times \unicode[STIX]{x1D708}\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C}$
(here we use a well known notation introduced in [Reference Zelevinsky17] for the normalized parabolic induction for the general linear groups with the usual choice of the standard parabolic subgroups). For integers
$\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}\times \cdots \times \unicode[STIX]{x1D708}\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D70C}$
(here we use a well known notation introduced in [Reference Zelevinsky17] for the normalized parabolic induction for the general linear groups with the usual choice of the standard parabolic subgroups). For integers
![]() $x,y$
,
$x,y$
,
![]() $x\leqslant y$
, we set
$x\leqslant y$
, we set
![]() $[x,y]=\{z\in \mathbb{Z}:x\leqslant z\leqslant y\}$
. For irreducible essentially square-integrable representation
$[x,y]=\{z\in \mathbb{Z}:x\leqslant z\leqslant y\}$
. For irreducible essentially square-integrable representation
![]() $\unicode[STIX]{x1D6FF}$
, there is the unique
$\unicode[STIX]{x1D6FF}$
, there is the unique
![]() $e(\unicode[STIX]{x1D6FF})\in \mathbb{R}$
such that
$e(\unicode[STIX]{x1D6FF})\in \mathbb{R}$
such that
![]() $\unicode[STIX]{x1D708}^{-e(\unicode[STIX]{x1D6FF})}\unicode[STIX]{x1D6FF}$
is unitarizable.
$\unicode[STIX]{x1D708}^{-e(\unicode[STIX]{x1D6FF})}\unicode[STIX]{x1D6FF}$
is unitarizable.
In order to keep our results uniform, we put
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])=1$
(the one-dimensional representation of the trivial group) if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])=1$
(the one-dimensional representation of the trivial group) if
![]() $a=b-1$
and
$a=b-1$
and
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])=0$
if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])=0$
if
![]() $a<b-1$
.
$a<b-1$
.
Throughout the paper we prefer to use the subrepresentation version of the Langlands classification and write the nontempered representation
![]() $\unicode[STIX]{x1D70B}\in \text{Irr}(G_{n})$
as the unique irreducible (Langlands) subrepresentation of the induced representation of the form
$\unicode[STIX]{x1D70B}\in \text{Irr}(G_{n})$
as the unique irreducible (Langlands) subrepresentation of the induced representation of the form
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\times \cdots \times \unicode[STIX]{x1D6FF}_{k}\rtimes \unicode[STIX]{x1D70F}$
, where
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\times \cdots \times \unicode[STIX]{x1D6FF}_{k}\rtimes \unicode[STIX]{x1D70F}$
, where
![]() $\unicode[STIX]{x1D70F}\in \text{Irr}(G_{n^{\prime }})$
is a tempered representation and
$\unicode[STIX]{x1D70F}\in \text{Irr}(G_{n^{\prime }})$
is a tempered representation and
![]() $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k}$
are irreducible essentially square-integrable representations such that
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k}$
are irreducible essentially square-integrable representations such that
![]() $e(\unicode[STIX]{x1D6FF}_{1})\leqslant e(\unicode[STIX]{x1D6FF}_{2})\leqslant \cdots \leqslant e(\unicode[STIX]{x1D6FF}_{k})<0$
. In this case, we write
$e(\unicode[STIX]{x1D6FF}_{1})\leqslant e(\unicode[STIX]{x1D6FF}_{2})\leqslant \cdots \leqslant e(\unicode[STIX]{x1D6FF}_{k})<0$
. In this case, we write
![]() $\unicode[STIX]{x1D70B}=L(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\times \cdots \times \unicode[STIX]{x1D6FF}_{k}\rtimes \unicode[STIX]{x1D70F})$
. Also, for simplicity of the notation, if
$\unicode[STIX]{x1D70B}=L(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\times \cdots \times \unicode[STIX]{x1D6FF}_{k}\rtimes \unicode[STIX]{x1D70F})$
. Also, for simplicity of the notation, if
![]() $\unicode[STIX]{x1D70F}\in \text{Irr}(G_{n})$
is a tempered representation and
$\unicode[STIX]{x1D70F}\in \text{Irr}(G_{n})$
is a tempered representation and
![]() $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k}$
are irreducible essentially square-integrable representations such that
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k}$
are irreducible essentially square-integrable representations such that
![]() $e(\unicode[STIX]{x1D6FF}_{i})<0$
for all
$e(\unicode[STIX]{x1D6FF}_{i})<0$
for all
![]() $i=1,2,\ldots ,k$
, we define
$i=1,2,\ldots ,k$
, we define
![]() $L(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k},\unicode[STIX]{x1D70F})$
to be
$L(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k},\unicode[STIX]{x1D70F})$
to be
![]() $L(\unicode[STIX]{x1D6FF}_{i_{1}}\times \unicode[STIX]{x1D6FF}_{i_{2}}\times \cdots \times \unicode[STIX]{x1D6FF}_{i_{k}}\rtimes \unicode[STIX]{x1D70F})$
, where
$L(\unicode[STIX]{x1D6FF}_{i_{1}}\times \unicode[STIX]{x1D6FF}_{i_{2}}\times \cdots \times \unicode[STIX]{x1D6FF}_{i_{k}}\rtimes \unicode[STIX]{x1D70F})$
, where
![]() $\unicode[STIX]{x1D6FF}_{i_{1}},\unicode[STIX]{x1D6FF}_{i_{2}},\ldots ,\unicode[STIX]{x1D6FF}_{i_{k}}$
is a permutation of
$\unicode[STIX]{x1D6FF}_{i_{1}},\unicode[STIX]{x1D6FF}_{i_{2}},\ldots ,\unicode[STIX]{x1D6FF}_{i_{k}}$
is a permutation of
![]() $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k}$
such that
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2},\ldots ,\unicode[STIX]{x1D6FF}_{k}$
such that
![]() $e(\unicode[STIX]{x1D6FF}_{i_{1}})\leqslant e(\unicode[STIX]{x1D6FF}_{i_{2}})\leqslant \cdots \leqslant e(\unicode[STIX]{x1D6FF}_{i_{k}})$
. We note that similar notation has been used in [Reference Tadić14].
$e(\unicode[STIX]{x1D6FF}_{i_{1}})\leqslant e(\unicode[STIX]{x1D6FF}_{i_{2}})\leqslant \cdots \leqslant e(\unicode[STIX]{x1D6FF}_{i_{k}})$
. We note that similar notation has been used in [Reference Tadić14].
Using Jacquet modules for the maximal standard parabolic subgroups of
![]() $\text{GL}(n,F)$
we can also define
$\text{GL}(n,F)$
we can also define
![]() $m^{\ast }(\unicode[STIX]{x1D70B})=\sum _{k=0}^{n}\text{s.s.}(r_{(k)}(\unicode[STIX]{x1D70B}))\in R(\text{GL})\otimes R(\text{GL})$
, for an irreducible representation
$m^{\ast }(\unicode[STIX]{x1D70B})=\sum _{k=0}^{n}\text{s.s.}(r_{(k)}(\unicode[STIX]{x1D70B}))\in R(\text{GL})\otimes R(\text{GL})$
, for an irreducible representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{GL}(n,F)$
, and then extend
$\text{GL}(n,F)$
, and then extend
![]() $m^{\ast }$
linearly to the whole of
$m^{\ast }$
linearly to the whole of
![]() $R(\text{GL})$
. Here
$R(\text{GL})$
. Here
![]() $r_{(k)}(\unicode[STIX]{x1D70B})$
denotes the normalized Jacquet module of
$r_{(k)}(\unicode[STIX]{x1D70B})$
denotes the normalized Jacquet module of
![]() $\unicode[STIX]{x1D70B}$
with respect to the standard parabolic subgroup having Levi factor equal to
$\unicode[STIX]{x1D70B}$
with respect to the standard parabolic subgroup having Levi factor equal to
![]() $\text{GL}(k,F)\times \text{GL}(n-k,F)$
.
$\text{GL}(k,F)\times \text{GL}(n-k,F)$
.
The following equation is frequently used in the paper:
Note that the multiplicativity of
![]() $m^{\ast }$
implies
$m^{\ast }$
implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle m^{\ast }\left(\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a_{j}}\unicode[STIX]{x1D70C}_{j},\unicode[STIX]{x1D708}^{b_{j}}\unicode[STIX]{x1D70C}_{j}])\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{j=1}^{n}\left(\mathop{\sum }_{i_{j}=a_{j}-1}^{b_{j}}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{j}+1}\unicode[STIX]{x1D70C}_{j},\unicode[STIX]{x1D708}^{b_{j}}\unicode[STIX]{x1D70C}_{j}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a_{j}}\unicode[STIX]{x1D70C}_{j},\unicode[STIX]{x1D708}^{i_{j}}\unicode[STIX]{x1D70C}_{j}])\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle m^{\ast }\left(\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a_{j}}\unicode[STIX]{x1D70C}_{j},\unicode[STIX]{x1D708}^{b_{j}}\unicode[STIX]{x1D70C}_{j}])\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{j=1}^{n}\left(\mathop{\sum }_{i_{j}=a_{j}-1}^{b_{j}}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{j}+1}\unicode[STIX]{x1D70C}_{j},\unicode[STIX]{x1D708}^{b_{j}}\unicode[STIX]{x1D70C}_{j}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a_{j}}\unicode[STIX]{x1D70C}_{j},\unicode[STIX]{x1D708}^{i_{j}}\unicode[STIX]{x1D70C}_{j}])\right).\nonumber\end{eqnarray}$$
For representation
![]() $\unicode[STIX]{x1D70E}\in R(G_{n})$
, we denote by
$\unicode[STIX]{x1D70E}\in R(G_{n})$
, we denote by
![]() $r_{P}(\unicode[STIX]{x1D70E})$
the normalized Jacquet module of
$r_{P}(\unicode[STIX]{x1D70E})$
the normalized Jacquet module of
![]() $\unicode[STIX]{x1D70E}$
with respect to the parabolic subgroup
$\unicode[STIX]{x1D70E}$
with respect to the parabolic subgroup
![]() $P$
. Furthermore, for
$P$
. Furthermore, for
![]() $1\leqslant k\leqslant n$
we denote by
$1\leqslant k\leqslant n$
we denote by
![]() $r_{(k)}(\unicode[STIX]{x1D70E})$
the normalized Jacquet module of
$r_{(k)}(\unicode[STIX]{x1D70E})$
the normalized Jacquet module of
![]() $\unicode[STIX]{x1D70E}$
with respect to the parabolic subgroup
$\unicode[STIX]{x1D70E}$
with respect to the parabolic subgroup
![]() $P_{(k)}$
having Levi subgroup equal to
$P_{(k)}$
having Levi subgroup equal to
![]() $\text{GL}(k,F)\times G_{n-k}$
. We identify
$\text{GL}(k,F)\times G_{n-k}$
. We identify
![]() $r_{(k)}(\unicode[STIX]{x1D70E})$
with its semisimplification in
$r_{(k)}(\unicode[STIX]{x1D70E})$
with its semisimplification in
![]() $R(\text{GL}(k,F))\otimes R(G_{n-k})$
and consider
$R(\text{GL}(k,F))\otimes R(G_{n-k})$
and consider
We take a moment to state the crucial structural formula for our calculations with Jacquet modules [Reference Tadić15], which is a version of the Geometrical lemma of Bernstein and Zelevinsky [Reference Bernstein and Zelevinsky2].
Lemma 2.1. Let
![]() $\unicode[STIX]{x1D70C}\in \text{Irr}(\text{GL}(m,F))$
be a cuspidal representation and
$\unicode[STIX]{x1D70C}\in \text{Irr}(\text{GL}(m,F))$
be a cuspidal representation and
![]() $k,l\in \mathbb{R}$
such that
$k,l\in \mathbb{R}$
such that
![]() $k+l\in \mathbb{Z}_{{\geqslant}0}$
. Let
$k+l\in \mathbb{Z}_{{\geqslant}0}$
. Let
![]() $\unicode[STIX]{x1D70E}$
be an admissible representation of finite length of
$\unicode[STIX]{x1D70E}$
be an admissible representation of finite length of
![]() $G_{n}$
. Write
$G_{n}$
. Write
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E})=\sum _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D70E}^{\prime }$
. Then the following holds:
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E})=\sum _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D70E}^{\prime }$
. Then the following holds:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-k}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{l}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}) & = & \displaystyle \mathop{\sum }_{i=-k-1}^{l}\mathop{\sum }_{j=i}^{l}\mathop{\sum }_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\widetilde{\unicode[STIX]{x1D70C}},\unicode[STIX]{x1D708}^{k}\widetilde{\unicode[STIX]{x1D70C}}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{l}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & \otimes & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{j}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-k}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{l}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}) & = & \displaystyle \mathop{\sum }_{i=-k-1}^{l}\mathop{\sum }_{j=i}^{l}\mathop{\sum }_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\widetilde{\unicode[STIX]{x1D70C}},\unicode[STIX]{x1D708}^{k}\widetilde{\unicode[STIX]{x1D70C}}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{l}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & \otimes & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{j}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}^{\prime }.\nonumber\end{eqnarray}$$
An irreducible representation
![]() $\unicode[STIX]{x1D70E}\in R(G)$
is called strongly positive if for every embedding
$\unicode[STIX]{x1D70E}\in R(G)$
is called strongly positive if for every embedding
where
![]() $\unicode[STIX]{x1D70C}_{i}\in R(\text{GL}(n_{\unicode[STIX]{x1D70C}_{i}},F))$
,
$\unicode[STIX]{x1D70C}_{i}\in R(\text{GL}(n_{\unicode[STIX]{x1D70C}_{i}},F))$
,
![]() $i=1,2,\ldots ,k$
, are cuspidal unitary representations and
$i=1,2,\ldots ,k$
, are cuspidal unitary representations and
![]() $\unicode[STIX]{x1D70E}_{cusp}\in R(G)$
is an irreducible cuspidal representation, we have
$\unicode[STIX]{x1D70E}_{cusp}\in R(G)$
is an irreducible cuspidal representation, we have
![]() $s_{i}>0$
for each
$s_{i}>0$
for each
![]() $i$
.
$i$
.
Obviously, every strongly positive representation is square-integrable. Irreducible strongly positive representations are called strongly positive discrete series.
Let us recall an inductive description of nonsupercuspidal strongly positive discrete series, which has been obtained in [Reference Matić4]. We note that the partial cuspidal support of an irreducible representation
![]() $\unicode[STIX]{x1D70E}\in R(G_{n})$
is an irreducible cuspidal representation
$\unicode[STIX]{x1D70E}\in R(G_{n})$
is an irreducible cuspidal representation
![]() $\unicode[STIX]{x1D70E}_{cusp}$
of some
$\unicode[STIX]{x1D70E}_{cusp}$
of some
![]() $R(n^{\prime })$
,
$R(n^{\prime })$
,
![]() $n^{\prime }\leqslant n$
, such that there exists a representation
$n^{\prime }\leqslant n$
, such that there exists a representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\text{GL}(n-n^{\prime },F)$
such that
$\text{GL}(n-n^{\prime },F)$
such that
![]() $\unicode[STIX]{x1D70E}{\hookrightarrow}\unicode[STIX]{x1D70B}\rtimes \unicode[STIX]{x1D70E}_{cusp}$
.
$\unicode[STIX]{x1D70E}{\hookrightarrow}\unicode[STIX]{x1D70B}\rtimes \unicode[STIX]{x1D70E}_{cusp}$
.
Proposition 2.2. Suppose that
![]() $\unicode[STIX]{x1D70E}\in R(G_{n})$
is an irreducible strongly positive representation and let
$\unicode[STIX]{x1D70E}\in R(G_{n})$
is an irreducible strongly positive representation and let
![]() $\unicode[STIX]{x1D70C}\in \text{Irr}(\text{GL}(m,F))$
denote an irreducible cuspidal representation such that some twist of
$\unicode[STIX]{x1D70C}\in \text{Irr}(\text{GL}(m,F))$
denote an irreducible cuspidal representation such that some twist of
![]() $\unicode[STIX]{x1D70C}$
appears in the cuspidal support of
$\unicode[STIX]{x1D70C}$
appears in the cuspidal support of
![]() $\unicode[STIX]{x1D70E}$
. We denote by
$\unicode[STIX]{x1D70E}$
. We denote by
![]() $\unicode[STIX]{x1D70E}_{cusp}$
the partial cuspidal support of
$\unicode[STIX]{x1D70E}_{cusp}$
the partial cuspidal support of
![]() $\unicode[STIX]{x1D70E}$
. Then there exist unique
$\unicode[STIX]{x1D70E}$
. Then there exist unique
![]() $a,b\in \mathbb{R}$
such that
$a,b\in \mathbb{R}$
such that
![]() $a>0,b>0$
,
$a>0,b>0$
,
![]() $b-a\in \mathbb{Z}_{{\geqslant}0}$
, and a unique irreducible strongly positive representation
$b-a\in \mathbb{Z}_{{\geqslant}0}$
, and a unique irreducible strongly positive representation
![]() $\unicode[STIX]{x1D70E}^{\prime }$
without
$\unicode[STIX]{x1D70E}^{\prime }$
without
![]() $\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}$
in the cuspidal support, with the property that
$\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}$
in the cuspidal support, with the property that
![]() $\unicode[STIX]{x1D70E}$
is a unique irreducible subrepresentation of
$\unicode[STIX]{x1D70E}$
is a unique irreducible subrepresentation of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}^{\prime }$
. Furthermore, there is a nonnegative integer
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}^{\prime }$
. Furthermore, there is a nonnegative integer
![]() $l$
such that
$l$
such that
![]() $a+l=s$
, where
$a+l=s$
, where
![]() $s>0$
is such that
$s>0$
is such that
![]() $\unicode[STIX]{x1D708}^{s}\unicode[STIX]{x1D70C}\rtimes \unicode[STIX]{x1D70E}_{cusp}$
reduces. If
$\unicode[STIX]{x1D708}^{s}\unicode[STIX]{x1D70C}\rtimes \unicode[STIX]{x1D70E}_{cusp}$
reduces. If
![]() $l=0$
there are no twists of
$l=0$
there are no twists of
![]() $\unicode[STIX]{x1D70C}$
appearing in the cuspidal support of
$\unicode[STIX]{x1D70C}$
appearing in the cuspidal support of
![]() $\unicode[STIX]{x1D70E}^{\prime }$
and if
$\unicode[STIX]{x1D70E}^{\prime }$
and if
![]() $l>0$
there exist a unique
$l>0$
there exist a unique
![]() $b^{\prime }>b$
and a unique strongly positive discrete series
$b^{\prime }>b$
and a unique strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}^{\prime \prime }$
, which contains neither
$\unicode[STIX]{x1D70E}^{\prime \prime }$
, which contains neither
![]() $\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}$
nor
$\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}$
nor
![]() $\unicode[STIX]{x1D708}^{a+1}\unicode[STIX]{x1D70C}$
in its cuspidal support, such that
$\unicode[STIX]{x1D708}^{a+1}\unicode[STIX]{x1D70C}$
in its cuspidal support, such that
![]() $\unicode[STIX]{x1D70E}^{\prime }$
can be written as a unique irreducible subrepresentation of
$\unicode[STIX]{x1D70E}^{\prime }$
can be written as a unique irreducible subrepresentation of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b^{\prime }}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}^{\prime \prime }$
.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b^{\prime }}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}^{\prime \prime }$
.
We emphasize that if
![]() $\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}$
appears in the cuspidal support of
$\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}$
appears in the cuspidal support of
![]() $\unicode[STIX]{x1D70E}$
then
$\unicode[STIX]{x1D70E}$
then
![]() $\unicode[STIX]{x1D70C}$
is selfcontragredient and
$\unicode[STIX]{x1D70C}$
is selfcontragredient and
![]() $2x\in \mathbb{Z}$
[Reference Mœglin11, Reference Mœglin and Tadić12].
$2x\in \mathbb{Z}$
[Reference Mœglin11, Reference Mœglin and Tadić12].
By the Mœglin–Tadić classification, strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}$
corresponds to the so-called admissible triple of alternated type. Admissible triple corresponding to discrete series
$\unicode[STIX]{x1D70E}$
corresponds to the so-called admissible triple of alternated type. Admissible triple corresponding to discrete series
![]() $\unicode[STIX]{x1D70E}$
is an ordered triple of the form
$\unicode[STIX]{x1D70E}$
is an ordered triple of the form
![]() $(\text{Jord},\unicode[STIX]{x1D70E}_{cusp},\unicode[STIX]{x1D716})$
, where
$(\text{Jord},\unicode[STIX]{x1D70E}_{cusp},\unicode[STIX]{x1D716})$
, where
![]() $\text{Jord}$
(the set Jordan blocks) is the set of pairs
$\text{Jord}$
(the set Jordan blocks) is the set of pairs
![]() $(c,\unicode[STIX]{x1D70C})$
where
$(c,\unicode[STIX]{x1D70C})$
where
![]() $c$
is an integer of the appropriate parity and
$c$
is an integer of the appropriate parity and
![]() $\unicode[STIX]{x1D70C}$
an irreducible cuspidal selfcontragredient representation of general linear group,
$\unicode[STIX]{x1D70C}$
an irreducible cuspidal selfcontragredient representation of general linear group,
![]() $\unicode[STIX]{x1D70E}_{cusp}$
is the partial cuspidal support of
$\unicode[STIX]{x1D70E}_{cusp}$
is the partial cuspidal support of
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D716}$
is a function defined on the subset of
$\unicode[STIX]{x1D716}$
is a function defined on the subset of
![]() $\text{Jord}\times \text{Jord}\cup \text{Jord}$
into
$\text{Jord}\times \text{Jord}\cup \text{Jord}$
into
![]() $\{\pm 1\}$
. For irreducible cuspidal selfcontragredient representation
$\{\pm 1\}$
. For irreducible cuspidal selfcontragredient representation
![]() $\unicode[STIX]{x1D70C}$
of general linear group we define
$\unicode[STIX]{x1D70C}$
of general linear group we define
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}=\{c:(c,\unicode[STIX]{x1D70C})\in \text{Jord}\}$
and for
$\text{Jord}_{\unicode[STIX]{x1D70C}}=\{c:(c,\unicode[STIX]{x1D70C})\in \text{Jord}\}$
and for
![]() $c\in \text{Jord}_{\unicode[STIX]{x1D70C}}$
we write
$c\in \text{Jord}_{\unicode[STIX]{x1D70C}}$
we write
![]() $c\_$
for maximum of the set
$c\_$
for maximum of the set
![]() $\{c^{\prime }\in \text{Jord}_{\unicode[STIX]{x1D70C}}:c^{\prime }<c\}$
if this set is nonempty. An admissible triple
$\{c^{\prime }\in \text{Jord}_{\unicode[STIX]{x1D70C}}:c^{\prime }<c\}$
if this set is nonempty. An admissible triple
![]() $(\text{Jord},\unicode[STIX]{x1D70E}_{cusp},\unicode[STIX]{x1D716})$
is called a triple of alternated type if for every
$(\text{Jord},\unicode[STIX]{x1D70E}_{cusp},\unicode[STIX]{x1D716})$
is called a triple of alternated type if for every
![]() $(c,\unicode[STIX]{x1D70C})\in \text{Jord}$
such that
$(c,\unicode[STIX]{x1D70C})\in \text{Jord}$
such that
![]() $c\_$
is defined holds
$c\_$
is defined holds
![]() $\unicode[STIX]{x1D716}((c\_,\unicode[STIX]{x1D70C}),(c,\unicode[STIX]{x1D70C}))=-1$
. By definition of such triples, a strongly positive discrete series is completely determined by its partial cuspidal support and the set of Jordan blocks. Since all strongly positive discrete series which we study in this paper share a common partial cuspidal support, we define only the set of Jordan blocks when introducing them. Similar procedure has also been summarized in [Reference Muić13, Proposition 1.2].
$\unicode[STIX]{x1D716}((c\_,\unicode[STIX]{x1D70C}),(c,\unicode[STIX]{x1D70C}))=-1$
. By definition of such triples, a strongly positive discrete series is completely determined by its partial cuspidal support and the set of Jordan blocks. Since all strongly positive discrete series which we study in this paper share a common partial cuspidal support, we define only the set of Jordan blocks when introducing them. Similar procedure has also been summarized in [Reference Muić13, Proposition 1.2].
Through the paper we denote the set of Jordan blocks corresponding to discrete series
![]() $\unicode[STIX]{x1D70E}$
by
$\unicode[STIX]{x1D70E}$
by
![]() $\text{Jord}(\unicode[STIX]{x1D70E})$
and set
$\text{Jord}(\unicode[STIX]{x1D70E})$
and set
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E})=\{c:(c,\unicode[STIX]{x1D70C})\in \text{Jord}(\unicode[STIX]{x1D70E})\}$
.
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E})=\{c:(c,\unicode[STIX]{x1D70C})\in \text{Jord}(\unicode[STIX]{x1D70E})\}$
.
If
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
, we may assume
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
, we may assume
![]() $b\leqslant d$
, since in Grothendieck group we have
$b\leqslant d$
, since in Grothendieck group we have
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}=\unicode[STIX]{x1D6FF}_{2}\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Also, if
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}=\unicode[STIX]{x1D6FF}_{2}\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Also, if
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and
![]() $b=d$
, through the paper we additionally assume
$b=d$
, through the paper we additionally assume
![]() $a\leqslant c$
.
$a\leqslant c$
.
3 Some technical results
Proposition 3.1. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and let
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and let
![]() $\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}_{1}^{\prime }\times \unicode[STIX]{x1D6FF}_{2}^{\prime }\times \cdots \times \unicode[STIX]{x1D6FF}_{k}^{\prime }\rtimes \unicode[STIX]{x1D70F})$
, where
$\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}_{1}^{\prime }\times \unicode[STIX]{x1D6FF}_{2}^{\prime }\times \cdots \times \unicode[STIX]{x1D6FF}_{k}^{\prime }\rtimes \unicode[STIX]{x1D70F})$
, where
![]() $\unicode[STIX]{x1D6FF}_{1}^{\prime },\unicode[STIX]{x1D6FF}_{2}^{\prime },\ldots ,\unicode[STIX]{x1D6FF}_{k}^{\prime }$
are irreducible essentially square-integrable representations such that
$\unicode[STIX]{x1D6FF}_{1}^{\prime },\unicode[STIX]{x1D6FF}_{2}^{\prime },\ldots ,\unicode[STIX]{x1D6FF}_{k}^{\prime }$
are irreducible essentially square-integrable representations such that
![]() $e(\unicode[STIX]{x1D6FF}_{i}^{\prime })<0$
for all
$e(\unicode[STIX]{x1D6FF}_{i}^{\prime })<0$
for all
![]() $i$
and
$i$
and
![]() $e(\unicode[STIX]{x1D6FF}_{i-1}^{\prime })\leqslant e(\unicode[STIX]{x1D6FF}_{i}^{\prime })$
holds for
$e(\unicode[STIX]{x1D6FF}_{i-1}^{\prime })\leqslant e(\unicode[STIX]{x1D6FF}_{i}^{\prime })$
holds for
![]() $i=2,\ldots ,k$
, and
$i=2,\ldots ,k$
, and
![]() $\unicode[STIX]{x1D70F}$
is a tempered representation of
$\unicode[STIX]{x1D70F}$
is a tempered representation of
![]() $G_{n^{\prime }}$
. Then
$G_{n^{\prime }}$
. Then
![]() $k\leqslant 2$
and
$k\leqslant 2$
and
![]() $\unicode[STIX]{x1D70F}$
is strongly positive.
$\unicode[STIX]{x1D70F}$
is strongly positive.
Proof. From the cuspidal support of the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, using description of strongly positive discrete series and
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, using description of strongly positive discrete series and
![]() $a\geqslant 1$
,
$a\geqslant 1$
,
![]() $c\geqslant 1$
, we deduce that
$c\geqslant 1$
, we deduce that
![]() $\unicode[STIX]{x1D70F}$
has to be strongly positive.
$\unicode[STIX]{x1D70F}$
has to be strongly positive.
Let us assume, on the contrary, that there is an irreducible constituent
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
of the form
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
of the form
![]() $L(\unicode[STIX]{x1D6FF}_{1}^{\prime }\times \unicode[STIX]{x1D6FF}_{2}^{\prime }\times \cdots \times \unicode[STIX]{x1D6FF}_{k}^{\prime }\rtimes \unicode[STIX]{x1D70F})$
, with
$L(\unicode[STIX]{x1D6FF}_{1}^{\prime }\times \unicode[STIX]{x1D6FF}_{2}^{\prime }\times \cdots \times \unicode[STIX]{x1D6FF}_{k}^{\prime }\rtimes \unicode[STIX]{x1D70F})$
, with
![]() $k\geqslant 3$
. We write
$k\geqslant 3$
. We write
![]() $\unicode[STIX]{x1D6FF}_{i}^{\prime }=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x_{i}}\unicode[STIX]{x1D70C}_{i}^{\prime },\unicode[STIX]{x1D708}^{y_{i}}\unicode[STIX]{x1D70C}_{i}^{\prime }])$
. Obviously, we have
$\unicode[STIX]{x1D6FF}_{i}^{\prime }=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x_{i}}\unicode[STIX]{x1D70C}_{i}^{\prime },\unicode[STIX]{x1D708}^{y_{i}}\unicode[STIX]{x1D70C}_{i}^{\prime }])$
. Obviously, we have
![]() $x_{i}+y_{i}<0$
for
$x_{i}+y_{i}<0$
for
![]() $i=1,2,\ldots ,k$
and
$i=1,2,\ldots ,k$
and
![]() $x_{i}+y_{i}\leqslant x_{i+1}+y_{i+1}$
for
$x_{i}+y_{i}\leqslant x_{i+1}+y_{i+1}$
for
![]() $i=1,2,\ldots ,k-1$
.
$i=1,2,\ldots ,k-1$
.
Frobenius reciprocity implies that
![]() $\unicode[STIX]{x1D6FF}_{1}^{\prime }\otimes \unicode[STIX]{x1D6FF}_{2}^{\prime }\otimes \cdots \otimes \unicode[STIX]{x1D6FF}_{k}^{\prime }\otimes \unicode[STIX]{x1D70F}$
is contained in the Jacquet module of
$\unicode[STIX]{x1D6FF}_{1}^{\prime }\otimes \unicode[STIX]{x1D6FF}_{2}^{\prime }\otimes \cdots \otimes \unicode[STIX]{x1D6FF}_{k}^{\prime }\otimes \unicode[STIX]{x1D70F}$
is contained in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}$
with respect to the appropriate parabolic subgroup. Since
$\unicode[STIX]{x1D70B}$
with respect to the appropriate parabolic subgroup. Since
![]() $\unicode[STIX]{x1D70B}$
is a subquotient of
$\unicode[STIX]{x1D70B}$
is a subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, using transitivity of Jacquet modules, we deduce that there is an irreducible representation
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, using transitivity of Jacquet modules, we deduce that there is an irreducible representation
![]() $\unicode[STIX]{x1D70F}_{1}$
of
$\unicode[STIX]{x1D70F}_{1}$
of
![]() $G_{n_{1}}$
such that
$G_{n_{1}}$
such that
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})\geqslant \unicode[STIX]{x1D6FF}_{1}^{\prime }\otimes \unicode[STIX]{x1D70F}_{1}$
. Using Lemma 2.1 twice, we deduce that there are
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})\geqslant \unicode[STIX]{x1D6FF}_{1}^{\prime }\otimes \unicode[STIX]{x1D70F}_{1}$
. Using Lemma 2.1 twice, we deduce that there are
![]() $t_{1}^{(1)}$
,
$t_{1}^{(1)}$
,
![]() $t_{2}^{(1)}$
,
$t_{2}^{(1)}$
,
![]() $s_{1}^{(1)}$
,
$s_{1}^{(1)}$
,
![]() $s_{2}^{(1)}$
such that
$s_{2}^{(1)}$
such that
![]() $a-1\leqslant t_{1}^{(1)}\leqslant s_{1}^{(1)}\leqslant b$
,
$a-1\leqslant t_{1}^{(1)}\leqslant s_{1}^{(1)}\leqslant b$
,
![]() $c-1\leqslant t_{2}^{(1)}\leqslant s_{2}^{(1)}\leqslant d$
and an irreducible constituent
$c-1\leqslant t_{2}^{(1)}\leqslant s_{2}^{(1)}\leqslant d$
and an irreducible constituent
![]() $\unicode[STIX]{x1D70B}_{1}\otimes \unicode[STIX]{x1D70E}_{1}$
of
$\unicode[STIX]{x1D70B}_{1}\otimes \unicode[STIX]{x1D70E}_{1}$
of
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E}_{sp})$
such that
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E}_{sp})$
such that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x_{1}}\unicode[STIX]{x1D70C}_{1}^{\prime },\unicode[STIX]{x1D708}^{y_{1}}\unicode[STIX]{x1D70C}_{1}^{\prime }]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-t_{1}^{(1)}}\widetilde{\unicode[STIX]{x1D70C}_{1}},\unicode[STIX]{x1D708}^{-a}\widetilde{\unicode[STIX]{x1D70C}_{1}}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{s_{1}^{(1)}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-t_{2}^{(1)}}\widetilde{\unicode[STIX]{x1D70C}_{2}},\unicode[STIX]{x1D708}^{-c}\widetilde{\unicode[STIX]{x1D70C}_{2}}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{s_{2}^{(1)}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D70B}_{1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x_{1}}\unicode[STIX]{x1D70C}_{1}^{\prime },\unicode[STIX]{x1D708}^{y_{1}}\unicode[STIX]{x1D70C}_{1}^{\prime }]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-t_{1}^{(1)}}\widetilde{\unicode[STIX]{x1D70C}_{1}},\unicode[STIX]{x1D708}^{-a}\widetilde{\unicode[STIX]{x1D70C}_{1}}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{s_{1}^{(1)}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-t_{2}^{(1)}}\widetilde{\unicode[STIX]{x1D70C}_{2}},\unicode[STIX]{x1D708}^{-c}\widetilde{\unicode[STIX]{x1D70C}_{2}}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{s_{2}^{(1)}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D70B}_{1}\nonumber\end{eqnarray}$$
and
Definition of strongly positive discrete series implies that if
![]() $\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}$
appears in cuspidal support of
$\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D70C}$
appears in cuspidal support of
![]() $\unicode[STIX]{x1D70B}_{1}$
, then
$\unicode[STIX]{x1D70B}_{1}$
, then
![]() $m>0$
. Since
$m>0$
. Since
![]() $x_{1}<0$
, from
$x_{1}<0$
, from
![]() $-a\leqslant -1$
,
$-a\leqslant -1$
,
![]() $-c\leqslant -1$
,
$-c\leqslant -1$
,
![]() $s_{1}^{(1)}+1\geqslant 1$
and
$s_{1}^{(1)}+1\geqslant 1$
and
![]() $s_{2}^{(1)}+1\geqslant 1$
, we deduce that
$s_{2}^{(1)}+1\geqslant 1$
, we deduce that
![]() $s_{1}^{(1)}=b$
,
$s_{1}^{(1)}=b$
,
![]() $s_{2}^{(1)}=d$
and
$s_{2}^{(1)}=d$
and
![]() $\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}_{sp}$
. Also,
$\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}_{sp}$
. Also,
![]() $(y_{1},\unicode[STIX]{x1D70C}_{1}^{\prime })\in \{(-a,\widetilde{\unicode[STIX]{x1D70C}_{1}}),(-c,\widetilde{\unicode[STIX]{x1D70C}_{2}})\}$
.
$(y_{1},\unicode[STIX]{x1D70C}_{1}^{\prime })\in \{(-a,\widetilde{\unicode[STIX]{x1D70C}_{1}}),(-c,\widetilde{\unicode[STIX]{x1D70C}_{2}})\}$
.
Using transitivity of Jacquet modules again, we obtain that there is an irreducible representation
![]() $\unicode[STIX]{x1D70F}_{2}$
of
$\unicode[STIX]{x1D70F}_{2}$
of
![]() $G_{n_{2}}$
such that
$G_{n_{2}}$
such that
In the same way as before, we obtain that there are
![]() $t_{1}^{(2)}$
and
$t_{1}^{(2)}$
and
![]() $t_{2}^{(2)}$
such that
$t_{2}^{(2)}$
such that
![]() $t_{1}^{(1)}\leqslant t_{1}^{(2)}\leqslant b$
,
$t_{1}^{(1)}\leqslant t_{1}^{(2)}\leqslant b$
,
![]() $t_{2}^{(1)}\leqslant t_{2}^{(2)}\leqslant d$
and
$t_{2}^{(1)}\leqslant t_{2}^{(2)}\leqslant d$
and
Furthermore,
![]() $t_{1}^{(2)}\geqslant a$
and
$t_{1}^{(2)}\geqslant a$
and
![]() $t_{2}^{(2)}\geqslant c$
, since otherwise we would have
$t_{2}^{(2)}\geqslant c$
, since otherwise we would have
![]() $y_{2}=x_{1}-1$
which implies
$y_{2}=x_{1}-1$
which implies
![]() $e(\unicode[STIX]{x1D6FF}_{1}^{\prime })>e(\unicode[STIX]{x1D6FF}_{2}^{\prime })$
, a contradiction.
$e(\unicode[STIX]{x1D6FF}_{1}^{\prime })>e(\unicode[STIX]{x1D6FF}_{2}^{\prime })$
, a contradiction.
Repeating the same procedure, we deduce that there are
![]() $t_{1}^{(3)}$
and
$t_{1}^{(3)}$
and
![]() $t_{2}^{(3)}$
such that
$t_{2}^{(3)}$
such that
![]() $t_{1}^{(2)}\leqslant t_{1}^{(3)}\leqslant b$
,
$t_{1}^{(2)}\leqslant t_{1}^{(3)}\leqslant b$
,
![]() $t_{2}^{(2)}\leqslant t_{2}^{(3)}\leqslant d$
and
$t_{2}^{(2)}\leqslant t_{2}^{(3)}\leqslant d$
and
Let us denote by
![]() $i$
an element of
$i$
an element of
![]() $\{1,2\}$
such that
$\{1,2\}$
such that
![]() $x_{2}=-t_{i}^{(2)}$
. Such
$x_{2}=-t_{i}^{(2)}$
. Such
![]() $i$
is obviously unique.
$i$
is obviously unique.
If
![]() $y_{2}=-t_{i}^{(1)}-1$
, we have
$y_{2}=-t_{i}^{(1)}-1$
, we have
![]() $t_{j}^{(1)}=t_{j}^{(2)}$
for
$t_{j}^{(1)}=t_{j}^{(2)}$
for
![]() $j\in \{1,2\}$
,
$j\in \{1,2\}$
,
![]() $j\neq i$
. Furthermore, from
$j\neq i$
. Furthermore, from
![]() $e(\unicode[STIX]{x1D6FF}_{1}^{\prime })\leqslant e(\unicode[STIX]{x1D6FF}_{2}^{\prime })$
we get
$e(\unicode[STIX]{x1D6FF}_{1}^{\prime })\leqslant e(\unicode[STIX]{x1D6FF}_{2}^{\prime })$
we get
![]() $x_{1}=-t_{j}^{(1)}$
, that is,
$x_{1}=-t_{j}^{(1)}$
, that is,
![]() $x_{1}=-t_{j}^{(2)}$
.
$x_{1}=-t_{j}^{(2)}$
.
On the other hand, if
![]() $y_{2}=-t_{j}^{(1)}-1$
for
$y_{2}=-t_{j}^{(1)}-1$
for
![]() $j\in \{1,2\}$
,
$j\in \{1,2\}$
,
![]() $j\neq i$
, we have
$j\neq i$
, we have
![]() $t_{i}^{(1)}=t_{j}^{(2)}$
. Now
$t_{i}^{(1)}=t_{j}^{(2)}$
. Now
![]() $e(\unicode[STIX]{x1D6FF}_{1}^{\prime })\leqslant e(\unicode[STIX]{x1D6FF}_{2}^{\prime })$
implies
$e(\unicode[STIX]{x1D6FF}_{1}^{\prime })\leqslant e(\unicode[STIX]{x1D6FF}_{2}^{\prime })$
implies
![]() $x_{1}=-t_{i}^{(1)}$
, that is,
$x_{1}=-t_{i}^{(1)}$
, that is,
![]() $x_{1}=-t_{j}^{(2)}$
.
$x_{1}=-t_{j}^{(2)}$
.
From (3) we obtain
![]() $y_{3}\in \{-t_{1}^{(2)}-1,-t_{2}^{(2)}-1\}$
. Since
$y_{3}\in \{-t_{1}^{(2)}-1,-t_{2}^{(2)}-1\}$
. Since
![]() $\{-t_{1}^{(2)}-1,-t_{2}^{(2)}-1\}=\{-x_{1}-1,-x_{2}-1\}$
, there is some
$\{-t_{1}^{(2)}-1,-t_{2}^{(2)}-1\}=\{-x_{1}-1,-x_{2}-1\}$
, there is some
![]() $i^{\prime }\in \{1,2\}$
such that
$i^{\prime }\in \{1,2\}$
such that
![]() $e(\unicode[STIX]{x1D6FF}_{3}^{\prime })<e(\unicode[STIX]{x1D6FF}_{i^{\prime }}^{\prime })$
, which is impossible. This ends the proof.◻
$e(\unicode[STIX]{x1D6FF}_{3}^{\prime })<e(\unicode[STIX]{x1D6FF}_{i^{\prime }}^{\prime })$
, which is impossible. This ends the proof.◻
From the proof of the previous proposition we directly obtain the following results, which are used throughout the paper to determine possible irreducible subquotients of the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
Proposition 3.2. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is an irreducible subquotient of the induced representation
$\unicode[STIX]{x1D70B}$
is an irreducible subquotient of the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Then one of the following holds:
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Then one of the following holds:
-
(a)
 $\unicode[STIX]{x1D70B}$
is strongly positive.
$\unicode[STIX]{x1D70B}$
is strongly positive. -
(b)
 $\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70F})$
, where
$\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70F})$
, where
 $y<0$
,
$y<0$
,
 $\unicode[STIX]{x1D70F}$
is strongly positive, and there are
$\unicode[STIX]{x1D70F}$
is strongly positive, and there are
 $i$
and
$i$
and
 $j$
,
$j$
,
 $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
 $c-1\leqslant j\leqslant d$
such that
$c-1\leqslant j\leqslant d$
such that  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\nonumber\\ \displaystyle \unicode[STIX]{x1D70F} & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\nonumber\\ \displaystyle \unicode[STIX]{x1D70F} & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
-
(c)
 $\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}^{\prime }])\rtimes \unicode[STIX]{x1D70F})$
, where
$\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}^{\prime }])\rtimes \unicode[STIX]{x1D70F})$
, where
 $y<0$
,
$y<0$
,
 $y^{\prime }<0$
,
$y^{\prime }<0$
,
 $x+y\leqslant x^{\prime }+y^{\prime }$
,
$x+y\leqslant x^{\prime }+y^{\prime }$
,
 $\unicode[STIX]{x1D70F}$
is strongly positive, and there are
$\unicode[STIX]{x1D70F}$
is strongly positive, and there are
 $i$
and
$i$
and
 $j$
,
$j$
,
 $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
 $c-1\leqslant j\leqslant d$
such that
$c-1\leqslant j\leqslant d$
such that  $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}^{\prime }])\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant m^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]))\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}^{\prime }])\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant m^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]))\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
Proposition 3.3. Suppose that there are
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
such that
$c-1\leqslant j\leqslant d$
such that
![]() $(i,j)\neq (a-1,c-1)$
such that the induced representation
$(i,j)\neq (a-1,c-1)$
such that the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive irreducible subquotient
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive irreducible subquotient
![]() $\unicode[STIX]{x1D70F}$
. All possible irreducible subquotients of
$\unicode[STIX]{x1D70F}$
. All possible irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
arising from such choice of the ordered pair
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
arising from such choice of the ordered pair
![]() $(i,j)$
are given as follows:
$(i,j)$
are given as follows:
-
(a)
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70F})$
, if
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70F})$
, if
 $j=c-1$
;
$j=c-1$
; -
(b)
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70F})$
, if
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70F})$
, if
 $i=a-1$
;
$i=a-1$
; -
(c)
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
, if
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
, if
 $i\neq a-1$
,
$i\neq a-1$
,
 $j\neq c-1$
and the induced representation
$j\neq c-1$
and the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
is irreducible;
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
is irreducible; -
(d)
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
and
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
and
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
, if
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
, if
 $i\neq a-1$
,
$i\neq a-1$
,
 $j\neq c-1$
and the induced representation
$j\neq c-1$
and the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
reduces.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
reduces.
Proof. Let us first consider the case
![]() $j=c-1$
. The case
$j=c-1$
. The case
![]() $i=a-1$
can be handled in the same way. Suppose that we are in the case
$i=a-1$
can be handled in the same way. Suppose that we are in the case
![]() $(c)$
of the previous proposition. Then we have
$(c)$
of the previous proposition. Then we have
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}^{\prime }])\leqslant m^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]))$
. Using the formula for
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C}^{\prime },\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}^{\prime }])\leqslant m^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]))$
. Using the formula for
![]() $m^{\ast }$
, we obtain
$m^{\ast }$
, we obtain
![]() $y^{\prime }=x-1$
, which is impossible. Thus, we are in the case
$y^{\prime }=x-1$
, which is impossible. Thus, we are in the case
![]() $(b)$
of the previous proposition and
$(b)$
of the previous proposition and
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])$
.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])$
.
It remains to consider that case
![]() $i\neq a-1$
,
$i\neq a-1$
,
![]() $j\neq c-1$
. Using multiplicativity of
$j\neq c-1$
. Using multiplicativity of
![]() $m^{\ast }$
, we deduce
$m^{\ast }$
, we deduce
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i^{\prime }}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j^{\prime }}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
for
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y}\unicode[STIX]{x1D70C}])\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i^{\prime }}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j^{\prime }}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
for
![]() $i^{\prime }$
and
$i^{\prime }$
and
![]() $j^{\prime }$
such that
$j^{\prime }$
such that
![]() $a-1\leqslant i^{\prime }\leqslant i$
,
$a-1\leqslant i^{\prime }\leqslant i$
,
![]() $c-1\leqslant j^{\prime }\leqslant j$
. If
$c-1\leqslant j^{\prime }\leqslant j$
. If
![]() $i^{\prime }\neq a-1$
and
$i^{\prime }\neq a-1$
and
![]() $j^{\prime }\neq c-1$
, we have
$j^{\prime }\neq c-1$
, we have
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and union of segments
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and union of segments
![]() $[-i^{\prime },a]$
and
$[-i^{\prime },a]$
and
![]() $[-j^{\prime },c]$
is a segment. From
$[-j^{\prime },c]$
is a segment. From
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}])\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-i^{\prime }-1}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-j^{\prime }-1}\unicode[STIX]{x1D70C}_{2}])$
, using
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}])\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-i^{\prime }-1}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-j^{\prime }-1}\unicode[STIX]{x1D70C}_{2}])$
, using
![]() $x+y\leqslant x^{\prime }+y^{\prime }$
, we get
$x+y\leqslant x^{\prime }+y^{\prime }$
, we get
![]() $i=i^{\prime }$
or
$i=i^{\prime }$
or
![]() $j=j^{\prime }$
. Consequently, the induced representation
$j=j^{\prime }$
. Consequently, the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
reduces and we obtain possible irreducible subquotient of the form
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
reduces and we obtain possible irreducible subquotient of the form
![]() $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
. We note that in the case
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F})$
. We note that in the case
![]() $i=i^{\prime }$
and
$i=i^{\prime }$
and
![]() $j=j^{\prime }$
we have either
$j=j^{\prime }$
we have either
or
Now we discuss the case
![]() $i^{\prime }=a-1$
. The case
$i^{\prime }=a-1$
. The case
![]() $j^{\prime }=c-1$
can be handled in the same way. It follows that
$j^{\prime }=c-1$
can be handled in the same way. It follows that
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}])\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-j^{\prime }-1}\unicode[STIX]{x1D70C}_{2}])$
, and we have the following two possibilities:
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}])\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-j^{\prime }-1}\unicode[STIX]{x1D70C}_{2}])$
, and we have the following two possibilities:
-
∙
 $j^{\prime }=j$
, which provides possible irreducible subquotient
$j^{\prime }=j$
, which provides possible irreducible subquotient  $$\begin{eqnarray}L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F}),\end{eqnarray}$$
$$\begin{eqnarray}L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F}),\end{eqnarray}$$
-
∙
 $j^{\prime }<j$
, and
$j^{\prime }<j$
, and
 $x+y\leqslant x^{\prime }+y^{\prime }$
now implies
$x+y\leqslant x^{\prime }+y^{\prime }$
now implies
 $i=j^{\prime }$
and
$i=j^{\prime }$
and
 $a<c$
. Consequently, the induced representation
$a<c$
. Consequently, the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
reduces and we again obtain possible irreducible subquotient
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])$
reduces and we again obtain possible irreducible subquotient  $$\begin{eqnarray}L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F}).\end{eqnarray}$$
$$\begin{eqnarray}L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-j}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70F}).\end{eqnarray}$$
This ends the proof. ◻
We take a moment to recall some results from [Reference Muić13], which are frequently used in the paper.
Lemma 3.4. Let
![]() $\unicode[STIX]{x1D70C}$
denote a supercuspidal element of
$\unicode[STIX]{x1D70C}$
denote a supercuspidal element of
![]() $\text{Irr}(\text{GL}(n_{\unicode[STIX]{x1D70C}},F))$
and
$\text{Irr}(\text{GL}(n_{\unicode[STIX]{x1D70C}},F))$
and
![]() $a,b\in \mathbb{R}$
such that
$a,b\in \mathbb{R}$
such that
![]() $a\leqslant b$
and
$a\leqslant b$
and
![]() $1\leqslant a$
. Let
$1\leqslant a$
. Let
![]() $\unicode[STIX]{x1D70E}_{sp}\in \text{Irr}(G_{n})$
stand for the strongly positive discrete series. Then the induced representation
$\unicode[STIX]{x1D70E}_{sp}\in \text{Irr}(G_{n})$
stand for the strongly positive discrete series. Then the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces if and only if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces if and only if
![]() $\unicode[STIX]{x1D70C}$
is selfcontragredient,
$\unicode[STIX]{x1D70C}$
is selfcontragredient,
![]() $[2a-1,2b-1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\neq \emptyset$
and
$[2a-1,2b-1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\neq \emptyset$
and
![]() $2b+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. If
$2b+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. If
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces, in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces, in
![]() $R(G)$
we have
$R(G)$
we have
for
![]() $x$
such that
$x$
such that
![]() $2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
and strongly positive discrete series
$2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
and strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2a-1,\unicode[STIX]{x1D70C})\}$
. In particular, the induced representation
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2a-1,\unicode[STIX]{x1D70C})\}$
. In particular, the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains an irreducible strongly positive subquotient if and only if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains an irreducible strongly positive subquotient if and only if
![]() $\unicode[STIX]{x1D70C}$
is selfcontragredient and
$\unicode[STIX]{x1D70C}$
is selfcontragredient and
![]() $\max ([2a-1,2b-1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}))=2a-1$
.
$\max ([2a-1,2b-1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}))=2a-1$
.
In the following two lemmas we recall necessary and sufficient conditions under which the representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series, which have been obtained in [Reference Matić7].
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series, which have been obtained in [Reference Matić7].
Lemma 3.5. The induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, where
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, where
![]() $\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
,
$\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
,
![]() $a\geqslant 1$
,
$a\geqslant 1$
,
![]() $c\geqslant 1$
, and
$c\geqslant 1$
, and
![]() $\unicode[STIX]{x1D70E}_{sp}\in \text{Irr}(G_{n})$
is a strongly positive discrete series, contains a strongly positive irreducible subquotient if and only if
$\unicode[STIX]{x1D70E}_{sp}\in \text{Irr}(G_{n})$
is a strongly positive discrete series, contains a strongly positive irreducible subquotient if and only if
![]() $\unicode[STIX]{x1D70C}_{i}$
is selfcontragredient for
$\unicode[STIX]{x1D70C}_{i}$
is selfcontragredient for
![]() $i=1,2$
,
$i=1,2$
,
![]() $[2a-1,2b+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})=\{2a-1\}$
and
$[2a-1,2b+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})=\{2a-1\}$
and
![]() $[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})=\{2c-1\}$
.
$[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})=\{2c-1\}$
.
Lemma 3.6. The induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, where
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, where
![]() $a\geqslant 1$
,
$a\geqslant 1$
,
![]() $c\geqslant 1$
,
$c\geqslant 1$
,
![]() $b\leqslant d$
, and
$b\leqslant d$
, and
![]() $\unicode[STIX]{x1D70E}_{sp}\in \text{Irr}(G_{n})$
is a strongly positive discrete series, contains a strongly positive irreducible subquotient if and only if
$\unicode[STIX]{x1D70E}_{sp}\in \text{Irr}(G_{n})$
is a strongly positive discrete series, contains a strongly positive irreducible subquotient if and only if
![]() $\unicode[STIX]{x1D70C}$
is selfcontragredient and one of the following holds:
$\unicode[STIX]{x1D70C}$
is selfcontragredient and one of the following holds:
-
(a)
 $[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})=\{2c-1\}$
and
$[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})=\{2c-1\}$
and
 $[2a-1,2b+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70B})=\{2a-1\}$
, for the unique irreducible strongly positive subquotient
$[2a-1,2b+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70B})=\{2a-1\}$
, for the unique irreducible strongly positive subquotient
 $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
. -
(b)
 $[2a-1,2b+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})=\{2a-1\}$
and
$[2a-1,2b+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})=\{2a-1\}$
and
 $[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70B})=\{2c-1\}$
, for the unique irreducible strongly positive subquotient
$[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70B})=\{2c-1\}$
, for the unique irreducible strongly positive subquotient
 $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
. -
(c)
 $c=b+1$
,
$c=b+1$
,
 $2a-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
,
$2a-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
,
 $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and if there is an
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and if there is an
 $x$
such that in
$x$
such that in
 $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
holds
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
holds
 $(2x+1)\_=2a-1$
then
$(2x+1)\_=2a-1$
then
 $d<x$
.
$d<x$
. -
(d)
 $c=b+1$
,
$c=b+1$
,
 $2a-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
,
$2a-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
,
 $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, there is an
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, there is an
 $x$
such that in
$x$
such that in
 $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
holds
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
holds
 $(2x+1)\_=2a-1$
and
$(2x+1)\_=2a-1$
and
 $[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})=\{2x+1\}$
.
$[2c-1,2d+1]\cap \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})=\{2x+1\}$
.
Let us also note a consequence of previous two lemmas.
Corollary 3.7. Suppose that there are
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $a-1\leqslant i\leqslant b$
and
$a-1\leqslant i\leqslant b$
and
![]() $c-1\leqslant j\leqslant d$
, such that the induced representation
$c-1\leqslant j\leqslant d$
, such that the induced representation
contains a strongly positive irreducible subquotient nonisomorphic to
![]() $\unicode[STIX]{x1D70E}_{sp}$
. Then at least one of the induced representations
$\unicode[STIX]{x1D70E}_{sp}$
. Then at least one of the induced representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces.
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces.
The following result is well known.
Lemma 3.8. Let
![]() $\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}$
denote admissible representations of finite length of
$\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}$
denote admissible representations of finite length of
![]() $G_{n}$
, such that
$G_{n}$
, such that
![]() $\unicode[STIX]{x1D70E}_{1}$
is irreducible subquotient of
$\unicode[STIX]{x1D70E}_{1}$
is irreducible subquotient of
![]() $\unicode[STIX]{x1D70E}_{3}$
and
$\unicode[STIX]{x1D70E}_{3}$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
is subquotient of
$\unicode[STIX]{x1D70E}_{2}$
is subquotient of
![]() $\unicode[STIX]{x1D70E}_{3}$
. If there is an irreducible representation
$\unicode[STIX]{x1D70E}_{3}$
. If there is an irreducible representation
![]() $\unicode[STIX]{x1D70B}$
such that
$\unicode[STIX]{x1D70B}$
such that
![]() $\unicode[STIX]{x1D70B}$
appears with multiplicity
$\unicode[STIX]{x1D70B}$
appears with multiplicity
![]() $m_{1}$
in
$m_{1}$
in
![]() $r_{P}(\unicode[STIX]{x1D70E}_{1})$
, with multiplicity
$r_{P}(\unicode[STIX]{x1D70E}_{1})$
, with multiplicity
![]() $m_{2}$
in
$m_{2}$
in
![]() $r_{P}(\unicode[STIX]{x1D70E}_{2})$
and with multiplicity
$r_{P}(\unicode[STIX]{x1D70E}_{2})$
and with multiplicity
![]() $m_{3}$
in
$m_{3}$
in
![]() $r_{P}(\unicode[STIX]{x1D70E}_{3})$
, for the appropriate parabolic subgroup
$r_{P}(\unicode[STIX]{x1D70E}_{3})$
, for the appropriate parabolic subgroup
![]() $P$
, and
$P$
, and
![]() $1\leqslant m_{1}\leqslant m_{2}=m_{3}$
, then
$1\leqslant m_{1}\leqslant m_{2}=m_{3}$
, then
![]() $\unicode[STIX]{x1D70E}_{1}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70E}_{1}$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D70E}_{2}$
.
$\unicode[STIX]{x1D70E}_{2}$
.
4 The case of irreducible
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
In this section we determine the composition factors of the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
in the first series of subcases. Through this section we assume that
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
in the first series of subcases. Through this section we assume that
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible. We note that in the case
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible. We note that in the case
![]() $\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
, the results follow immediately from [Reference Muić13] and [Reference Jantzen3]. We also note that the hypotheses needed to obtain the results from [Reference Muić13] and [Reference Jantzen3] are more restrictive.
$\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
, the results follow immediately from [Reference Muić13] and [Reference Jantzen3]. We also note that the hypotheses needed to obtain the results from [Reference Muić13] and [Reference Jantzen3] are more restrictive.
For simplicity of the notation, if
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
, let
$\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
, let
![]() $2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
. Also, if
$2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
. Also, if
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1]\neq \emptyset$
, let
$\text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1]\neq \emptyset$
, let
![]() $2y+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1])$
.
$2y+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1])$
.
The following proposition is well known:
Proposition 4.1. Suppose that both induced representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are irreducible. Then the induced representation
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are irreducible. Then the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible.
In the following two propositions we deal with the case when exactly one of the representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces.
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces.
Proposition 4.2. Suppose that the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and that the induced representation
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and that the induced representation
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible. Let
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible. Let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
stand for the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
stand for the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}_{1})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}_{1})\}$
. In
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}_{1})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}_{1})\}$
. In
![]() $R(G)$
we have
$R(G)$
we have
Proof. To determine possible irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
we use the approach introduced in Proposition 3.2, and determine all
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
we use the approach introduced in Proposition 3.2, and determine all
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
such that the induced representation
$c-1\leqslant j\leqslant d$
such that the induced representation
contains a strongly positive irreducible subquotient. Let us first prove that
![]() $j=d$
. If
$j=d$
. If
![]() $i=b$
, it follows directly from Lemma 3.4 that
$i=b$
, it follows directly from Lemma 3.4 that
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible for
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible for
![]() $j<d$
since
$j<d$
since
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible, and in this case there are no strongly positive subquotients. Now, let
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible, and in this case there are no strongly positive subquotients. Now, let
![]() $i<b$
. Irreducibility of
$i<b$
. Irreducibility of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, together with Lemma 3.4, show that situations described in Lemma 3.5 and in Lemmas 3.6(a) and 3.6(b) cannot happen. Assume that we are in the case of Lemma 3.6(c) or Lemma 3.6(d). Then
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, together with Lemma 3.4, show that situations described in Lemma 3.5 and in Lemmas 3.6(a) and 3.6(b) cannot happen. Assume that we are in the case of Lemma 3.6(c) or Lemma 3.6(d). Then
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and, since
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and, since
![]() $b\leqslant d$
,
$b\leqslant d$
,
![]() $j=b$
and
$j=b$
and
![]() $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})$
. This forces
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})$
. This forces
![]() $c\leqslant b+1$
and irreducibility of
$c\leqslant b+1$
and irreducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
gives
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
gives
![]() $c\leqslant a$
. But, reducibility of
$c\leqslant a$
. But, reducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and Lemma 3.4 show that
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and Lemma 3.4 show that
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces, a contradiction.
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces, a contradiction.
Consequently,
![]() $j=d$
and it can be directly verified that
$j=d$
and it can be directly verified that
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive subquotient only if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive subquotient only if
![]() $i\in \{b,x\}$
, for
$i\in \{b,x\}$
, for
![]() $x$
such that
$x$
such that
![]() $2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
.
$2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
.
Since
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible, Proposition 3.3 implies that
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible, Proposition 3.3 implies that
![]() $i=b$
and provides the irreducible subquotient
$i=b$
and provides the irreducible subquotient
![]() $L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
of
$L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
It remains to examine the case
![]() $i=x$
. If
$i=x$
. If
![]() $x=a-1$
, we are in the case of Proposition 3.3(a), which provides the irreducible representation
$x=a-1$
, we are in the case of Proposition 3.3(a), which provides the irreducible representation
![]() $L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
. If
$L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
. If
![]() $x\geqslant a$
, Proposition 3.3 provides the irreducible representation
$x\geqslant a$
, Proposition 3.3 provides the irreducible representation
![]() $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
.
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
.
It remains to prove that the obtained irreducible subquotient is contained in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
![]() $x=a-1$
,
$x=a-1$
,
![]() $L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is a subrepresentation of
$L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is a subrepresentation of
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
, which is contained in
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
, which is contained in
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
![]() $x\geqslant a$
,
$x\geqslant a$
,
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])$
is irreducible since
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])$
is irreducible since
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible. Thus,
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible. Thus,
and this induced representation has the unique irreducible subrepresentation
![]() $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
. Since
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
. Since
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is also a subrepresentation of
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is also a subrepresentation of
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
, we have
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
, we have
The equality
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}=\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
gives the desired conclusion.
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}=\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
gives the desired conclusion.
It is well known that
![]() $L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
is contained with multiplicity one in
$L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
is contained with multiplicity one in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Also, it is not hard to see that, if
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Also, it is not hard to see that, if
![]() $x=a-1$
,
$x=a-1$
,
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
appears in
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
appears in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
with multiplicity one, so
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
with multiplicity one, so
![]() $L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is contained in
$L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is contained in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one. Similarly, if
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one. Similarly, if
![]() $x>a-1$
, it follows directly from Lemma 2.1 that
$x>a-1$
, it follows directly from Lemma 2.1 that
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains the irreducible constituent
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains the irreducible constituent
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
with multiplicity one. This ends the proof.◻
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
with multiplicity one. This ends the proof.◻
Proposition 4.3. Suppose that the induced representation
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and that the induced representation
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and that the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible. Let
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible. Let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
stand for the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
stand for the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C}_{2})\}\cup \{(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
. In
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C}_{2})\}\cup \{(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
. In
![]() $R(G)$
we have
$R(G)$
we have
Proof. Again we start the determination of possible irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
by determining all
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
by determining all
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
such that the induced representation
$c-1\leqslant j\leqslant d$
such that the induced representation
contains a strongly positive irreducible subquotient. If
![]() $\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
, in the same way as in the proof of the previous proposition we get
$\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
, in the same way as in the proof of the previous proposition we get
![]() $i=b$
. Let us now consider the case
$i=b$
. Let us now consider the case
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
. Using irreducibility of
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
. Using irreducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, together with Lemma 3.4, we obtain that cases Lemmas 3.6(a), 3.6(b) and 3.6(c) do not appear. The case Lemma 3.6(d) appears if
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, together with Lemma 3.4, we obtain that cases Lemmas 3.6(a), 3.6(b) and 3.6(c) do not appear. The case Lemma 3.6(d) appears if
![]() $b<d$
,
$b<d$
,
![]() $j=b$
,
$j=b$
,
![]() $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $2i+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
(we note that
$2i+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
(we note that
![]() $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})$
since
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})$
since
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and irreducibility of
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and irreducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
implies
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
implies
![]() $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})$
). We denote the corresponding irreducible strongly positive subquotient of
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70E}_{sp})$
). We denote the corresponding irreducible strongly positive subquotient of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
by
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
by
![]() $\unicode[STIX]{x1D70E}_{sp}^{\prime }$
. Obviously,
$\unicode[STIX]{x1D70E}_{sp}^{\prime }$
. Obviously,
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{\prime })=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2i+1,\unicode[STIX]{x1D70C}_{1})\}\cup \{(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
.
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{\prime })=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2i+1,\unicode[STIX]{x1D70C}_{1})\}\cup \{(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
.
Since
![]() $b<d$
and
$b<d$
and
![]() $c\leqslant b+1$
, irreducibility of
$c\leqslant b+1$
, irreducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
gives
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
gives
![]() $c\leqslant a$
. We study two possibilities separately.
$c\leqslant a$
. We study two possibilities separately.
-
∙
 $i=a-1$
. Now we are in the case of Proposition 3.2(b) and we obtain a candidate
$i=a-1$
. Now we are in the case of Proposition 3.2(b) and we obtain a candidate
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime })$
for an irreducible constituent of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime })$
for an irreducible constituent of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Obviously,
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Obviously,
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime })$
is a subrepresentation of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime })$
is a subrepresentation of
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
and since, by Lemma 3.4,
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
and since, by Lemma 3.4, $$\begin{eqnarray}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\cong \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\cong \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime },\end{eqnarray}$$
 $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp}^{\prime })$
. Thus, it follows that
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp}^{\prime })$
. Thus, it follows that
 $\unicode[STIX]{x1D707}^{\ast }(L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime }))\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
. Consequently, if
$\unicode[STIX]{x1D707}^{\ast }(L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime }))\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
. Consequently, if
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime })$
is an irreducible subquotient of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{\prime })$
is an irreducible subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, then
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, then
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
. We analyze the last inequality using Lemma 2.1. There are
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
. We analyze the last inequality using Lemma 2.1. There are
 $a-1\leqslant i_{1}\leqslant j_{1}\leqslant b$
,
$a-1\leqslant i_{1}\leqslant j_{1}\leqslant b$
,
 $c-1\leqslant i_{2}\leqslant j_{2}\leqslant d$
and an irreducible constituent
$c-1\leqslant i_{2}\leqslant j_{2}\leqslant d$
and an irreducible constituent
 $\unicode[STIX]{x1D6FF}\otimes \unicode[STIX]{x1D70B}_{1}$
of
$\unicode[STIX]{x1D6FF}\otimes \unicode[STIX]{x1D70B}_{1}$
of
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E}_{sp})$
such that and
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E}_{sp})$
such that and $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{1}}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{2}}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}\nonumber\end{eqnarray}$$
We see at once that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{1}}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{2}}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}\nonumber\end{eqnarray}$$
We see at once that $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{j_{1}}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{j_{2}}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{j_{1}}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{j_{2}}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}. & & \displaystyle \nonumber\end{eqnarray}$$
 $i_{1}=a-1$
,
$i_{1}=a-1$
,
 $i_{2}=c-1$
,
$i_{2}=c-1$
,
 $j_{2}=d$
. From
$j_{2}=d$
. From
 $c\leqslant a$
and [Reference Matić6, Theorem 4.6] we deduce that
$c\leqslant a$
and [Reference Matić6, Theorem 4.6] we deduce that
 $j_{1}=a-1$
and
$j_{1}=a-1$
and
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{a-1}\unicode[STIX]{x1D70C}_{2}])$
. [Reference Matić6, Theorem 4.6] also gives that
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{a-1}\unicode[STIX]{x1D70C}_{2}])$
. [Reference Matić6, Theorem 4.6] also gives that
 $\unicode[STIX]{x1D70B}_{1}$
is strongly positive discrete series such that
$\unicode[STIX]{x1D70B}_{1}$
is strongly positive discrete series such that
 $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70B}_{1})$
. Consequently,
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{1}}(\unicode[STIX]{x1D70B}_{1})$
. Consequently,
 $\unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
, which is impossible since the induced representation
$\unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
, which is impossible since the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
does not contain irreducible strongly positive subquotient by Lemma 3.4.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
does not contain irreducible strongly positive subquotient by Lemma 3.4.
-
∙
 $i>a-1$
. Since union of the segments
$i>a-1$
. Since union of the segments
 $[-i,-a]$
and
$[-i,-a]$
and
 $[-b,-c]$
is not a segment, we are in the case of Proposition 3.3(c) and we obtain a candidate
$[-b,-c]$
is not a segment, we are in the case of Proposition 3.3(c) and we obtain a candidate
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
for an irreducible subquotient of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
for an irreducible subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.In the same way as in the previously considered case we obtain that the irreducible representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
is contained in the Jacquet module of the irreducible representation
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
is contained in the Jacquet module of the irreducible representation
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
with respect to the appropriate parabolic subgroup. Thus, if the irreducible representation
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
with respect to the appropriate parabolic subgroup. Thus, if the irreducible representation
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
is an irreducible subquotient of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
is an irreducible subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, using Lemma 2.1 and transitivity of Jacquet modules, we deduce that there are
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, using Lemma 2.1 and transitivity of Jacquet modules, we deduce that there are
 $i_{1}$
,
$i_{1}$
,
 $j_{1}$
,
$j_{1}$
,
 $i_{2}$
,
$i_{2}$
,
 $j_{2}$
such that
$j_{2}$
such that
 $a-1\leqslant i_{1}\leqslant j_{1}\leqslant b$
,
$a-1\leqslant i_{1}\leqslant j_{1}\leqslant b$
,
 $c-1\leqslant i_{2}\leqslant j_{2}\leqslant d$
, and an irreducible constituent
$c-1\leqslant i_{2}\leqslant j_{2}\leqslant d$
, and an irreducible constituent
 $\unicode[STIX]{x1D6FF}\otimes \unicode[STIX]{x1D70B}_{1}$
of
$\unicode[STIX]{x1D6FF}\otimes \unicode[STIX]{x1D70B}_{1}$
of
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E}_{sp})$
such that and
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70E}_{sp})$
such that and $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{1}}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{2}}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}\nonumber\end{eqnarray}$$
It is not hard to deduce that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{2}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{1}}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{2}}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}\nonumber\end{eqnarray}$$
It is not hard to deduce that $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{j_{1}}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{j_{2}}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{1}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{j_{1}}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{2}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{j_{2}}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}).\nonumber\end{eqnarray}$$
 $i_{1}=a-1$
,
$i_{1}=a-1$
,
 $i_{2}=c-1$
,
$i_{2}=c-1$
,
 $j_{2}=d$
. Also, by [Reference Matić6, Theorem 4.6], either
$j_{2}=d$
. Also, by [Reference Matić6, Theorem 4.6], either
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70E}_{sp}$
or
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70E}_{sp}$
or
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{2}])$
for
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{2}])$
for
 $2t+1=\min \{2z+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp}):c\leqslant z\}$
. Since
$2t+1=\min \{2z+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp}):c\leqslant z\}$
. Since
 $c\leqslant a$
and
$c\leqslant a$
and
 $2i+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
, it follows
$2i+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
, it follows
 $t\leqslant i$
.
$t\leqslant i$
.
If
 $c<a$
, then
$c<a$
, then
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{2}])$
and
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{2}])$
and
 $j_{1}=t$
. From
$j_{1}=t$
. From
 $t\leqslant i$
we get
$t\leqslant i$
we get
 $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70B}_{1})$
. It follows that
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}_{2}}(\unicode[STIX]{x1D70B}_{1})$
. It follows that
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
is an irreducible constituent of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }$
is an irreducible constituent of
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1})$
. Using the structural formula for
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1})$
. Using the structural formula for
 $\unicode[STIX]{x1D707}^{\ast }$
again, we see that there are
$\unicode[STIX]{x1D707}^{\ast }$
again, we see that there are
 $i_{3}$
,
$i_{3}$
,
 $j_{3}$
,
$j_{3}$
,
 $i_{4}$
,
$i_{4}$
,
 $j_{4}$
such that
$j_{4}$
such that
 $a-1\leqslant i_{3}\leqslant j_{3}\leqslant t$
,
$a-1\leqslant i_{3}\leqslant j_{3}\leqslant t$
,
 $c-1\leqslant i_{4}\leqslant j_{4}\leqslant d$
, and an irreducible constituent
$c-1\leqslant i_{4}\leqslant j_{4}\leqslant d$
, and an irreducible constituent
 $\unicode[STIX]{x1D6FF}^{\prime }\otimes \unicode[STIX]{x1D70B}_{2}$
of
$\unicode[STIX]{x1D6FF}^{\prime }\otimes \unicode[STIX]{x1D70B}_{2}$
of
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B}_{1})$
such that and
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B}_{1})$
such that and $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{3}}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{3}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{4}}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{4}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}^{\prime }\nonumber\end{eqnarray}$$
Since
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]) & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{3}}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{3}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i_{4}}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j_{4}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\times \unicode[STIX]{x1D6FF}^{\prime }\nonumber\end{eqnarray}$$
Since $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{3}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{j_{3}}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{4}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{j_{4}}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{2}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{3}+1}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{j_{3}}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i_{4}+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{j_{4}}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{2}. & & \displaystyle \nonumber\end{eqnarray}$$
 $a>0$
and
$a>0$
and
 $c<a$
, it directly follows that
$c<a$
, it directly follows that
 $j_{3}=t$
,
$j_{3}=t$
,
 $i_{4}=c-1$
,
$i_{4}=c-1$
,
 $j_{4}=d$
and
$j_{4}=d$
and
 $\unicode[STIX]{x1D70B}_{2}\cong \unicode[STIX]{x1D70B}_{1}$
. If
$\unicode[STIX]{x1D70B}_{2}\cong \unicode[STIX]{x1D70B}_{1}$
. If
 $t<i$
, it follows that the irreducible representation
$t<i$
, it follows that the irreducible representation
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
is not a subquotient of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{\prime })$
is not a subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Otherwise, we have
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. Otherwise, we have
 $i_{3}=t$
and
$i_{3}=t$
and
 $\unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
, which is impossible because it is a consequence of Lemma 3.4 that
$\unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
, which is impossible because it is a consequence of Lemma 3.4 that
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
does not contain an irreducible strongly positive subquotient.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
does not contain an irreducible strongly positive subquotient.
If
 $c=a$
and
$c=a$
and
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{2}])$
, then we again have
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{2}])$
, then we again have
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1})$
. In the same way as in the case
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1})$
. In the same way as in the case
 $c<a$
, we obtain that
$c<a$
, we obtain that
 $\unicode[STIX]{x1D70E}_{sp}^{\prime }$
is contained either in
$\unicode[STIX]{x1D70E}_{sp}^{\prime }$
is contained either in
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
(this can happen only if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
(this can happen only if
 $t=i$
) or in the induced representation
$t=i$
) or in the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
, but neither of these induced representations contains an irreducible strongly positive subquotient, by Lemmas 3.4 and 3.6.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{t}\unicode[STIX]{x1D70C}_{1}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
, but neither of these induced representations contains an irreducible strongly positive subquotient, by Lemmas 3.4 and 3.6.If
 $c=a$
and
$c=a$
and
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70E}_{sp}$
, then
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70E}_{sp}$
, then
 $j_{1}=a-1$
and
$j_{1}=a-1$
and
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp})$
. Following the same procedure as before we obtain
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-i}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}])\otimes \unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp})$
. Following the same procedure as before we obtain
 $\unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, which is impossible since Lemma 3.4 shows that the induced representation
$\unicode[STIX]{x1D70E}_{sp}^{\prime }\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, which is impossible since Lemma 3.4 shows that the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
does not contain an irreducible strongly positive subquotient.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}_{2}])\rtimes \unicode[STIX]{x1D70B}_{1}$
does not contain an irreducible strongly positive subquotient.
Consequently, we have proved that in (4) we must have
![]() $i=b$
. Now the rest of the proof follows the same lines as in the proof of Proposition 4.2.◻
$i=b$
. Now the rest of the proof follows the same lines as in the proof of Proposition 4.2.◻
In the rest of this section we determine composition factors of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
when
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
when
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible and both representations
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible and both representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduce. In this case, a description of the composition factors of
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduce. In this case, a description of the composition factors of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is divided in a sequence of lemmas.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is divided in a sequence of lemmas.
Lemma 4.4. Suppose that
![]() $\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
or
$\unicode[STIX]{x1D70C}_{1}\not \cong \unicode[STIX]{x1D70C}_{2}$
or
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and
![]() $x<y$
. Let
$x<y$
. Let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}_{1})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}_{1})\}$
,
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}_{1})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}_{1})\}$
,
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C}_{2})\}\cup \{(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
and
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C}_{2})\}\cup \{(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
and
![]() $\unicode[STIX]{x1D70E}_{sp}^{(3)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(3)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}_{1}),(2y+1,\unicode[STIX]{x1D70C}_{2})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}_{1}),(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
. In
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}_{1}),(2y+1,\unicode[STIX]{x1D70C}_{2})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}_{1}),(2d+1,\unicode[STIX]{x1D70C}_{2})\}$
. In
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{(3)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{(3)}).\nonumber\end{eqnarray}$$
Proof. It can be directly seen that
contains a strongly positive discrete series for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
if and only if
$c-1\leqslant j\leqslant d$
if and only if
![]() $(i,j)\in \{(b,d),(x,d),(b,y),(x,y)\}$
. If
$(i,j)\in \{(b,d),(x,d),(b,y),(x,y)\}$
. If
![]() $(i,j)=(x,y)$
and
$(i,j)=(x,y)$
and
![]() $(x,y)=(a-1,b-1)$
, we are in the case of Proposition 3.2(a) and
$(x,y)=(a-1,b-1)$
, we are in the case of Proposition 3.2(a) and
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains an irreducible strongly positive subquotient. If
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains an irreducible strongly positive subquotient. If
![]() $(i,j)\in \{(a-1,t_{1}),(t_{2},c-1)\}$
, for
$(i,j)\in \{(a-1,t_{1}),(t_{2},c-1)\}$
, for
![]() $t_{1}\neq c-1$
and
$t_{1}\neq c-1$
and
![]() $t_{2}\neq a-1$
, we are in the case Proposition 3.2(b), and in all other cases we are in the case of Proposition 3.2(c).
$t_{2}\neq a-1$
, we are in the case Proposition 3.2(b), and in all other cases we are in the case of Proposition 3.2(c).
Using our assumptions on
![]() $\unicode[STIX]{x1D6FF}_{1}$
and
$\unicode[STIX]{x1D6FF}_{1}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}$
, together with Proposition 3.3, we deduce that each of four possibilities for
$\unicode[STIX]{x1D6FF}_{2}$
, together with Proposition 3.3, we deduce that each of four possibilities for
![]() $(i,j)$
provides one candidate for the irreducible subquotient of
$(i,j)$
provides one candidate for the irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and all obtained candidates are mutually nonisomorphic. To show that the obtained candidate
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and all obtained candidates are mutually nonisomorphic. To show that the obtained candidate
![]() $\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
which appears with multiplicity one, we discuss only the case
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
which appears with multiplicity one, we discuss only the case
![]() $x>a-1$
,
$x>a-1$
,
![]() $y>b-1$
and
$y>b-1$
and
![]() $\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{(3)})$
. Other cases can be handled in an analogous way. We have
$\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}_{1}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}_{2}]),\unicode[STIX]{x1D70E}_{sp}^{(3)})$
. Other cases can be handled in an analogous way. We have
and
and it can be easily seen that both representations
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are contained in the induced representation
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are contained in the induced representation
Furthermore, Frobenius reciprocity shows that
appears in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}$
with respect to the appropriate parabolic subgroup, and structural formula can be used to obtain that the same irreducible representation appears with multiplicity one in the Jacquet module of
$\unicode[STIX]{x1D70B}$
with respect to the appropriate parabolic subgroup, and structural formula can be used to obtain that the same irreducible representation appears with multiplicity one in the Jacquet module of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with respect to the appropriate parabolic subgroup and in the Jacquet modules of
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with respect to the appropriate parabolic subgroup and in the Jacquet modules of
![]() $\unicode[STIX]{x1D70B}^{\prime }$
with respect to the appropriate parabolic subgroup. Lemma 3.8 shows that
$\unicode[STIX]{x1D70B}^{\prime }$
with respect to the appropriate parabolic subgroup. Lemma 3.8 shows that
![]() $\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and we have also proved that it appears with multiplicity one.◻
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and we have also proved that it appears with multiplicity one.◻
In the rest of this section we suppose
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and, for simplicity of the notation, we write
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and, for simplicity of the notation, we write
![]() $\unicode[STIX]{x1D70C}$
instead of
$\unicode[STIX]{x1D70C}$
instead of
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
.
$\unicode[STIX]{x1D70C}_{2}$
.
Lemma 4.5. Suppose that
![]() $b=d$
and let
$b=d$
and let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
. If
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
. If
![]() $a=c$
, in
$a=c$
, in
![]() $R(G)$
we have
$R(G)$
we have
If
![]() $a\neq c$
, we can assume
$a\neq c$
, we can assume
![]() $a<c$
. Then in
$a<c$
. Then in
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)}).\nonumber\end{eqnarray}$$
Proof. Obviously,
![]() $x=y$
. Induced representation
$x=y$
. Induced representation
contains a strongly positive discrete series for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant b$
if and only if
$c-1\leqslant j\leqslant b$
if and only if
![]() $(i,j)\in \{(b,b),(x,b),(b,x)\}$
.
$(i,j)\in \{(b,b),(x,b),(b,x)\}$
.
Let us first consider the case
![]() $a=c$
.
$a=c$
.
For
![]() $(i,j)\neq (b,b)$
, we obtain possible irreducible subquotient
$(i,j)\neq (b,b)$
, we obtain possible irreducible subquotient
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
of the form
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
of the form
![]() $\unicode[STIX]{x1D70B}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})$
if
$\unicode[STIX]{x1D70B}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})$
if
![]() $x>a-1$
, and of the form
$x>a-1$
, and of the form
![]() $\unicode[STIX]{x1D70B}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
, if
$\unicode[STIX]{x1D70B}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
, if
![]() $x=a-1$
.
$x=a-1$
.
If
![]() $x>a-1$
, then
$x>a-1$
, then
![]() $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is a subrepresentation of
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is a subrepresentation of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and if
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and if
![]() $x=a-1$
then
$x=a-1$
then
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
is a subrepresentation of
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
is a subrepresentation of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
. In the same way as in the proof of Proposition 4.2 we see
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
. In the same way as in the proof of Proposition 4.2 we see
![]() $\unicode[STIX]{x1D70B}\leqslant \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D70B}\leqslant \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
If
![]() $x>a-1$
, we have the following embeddings and isomorphisms:
$x>a-1$
, we have the following embeddings and isomorphisms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B} & {\hookrightarrow} & \displaystyle \widetilde{\unicode[STIX]{x1D6FF}_{1}}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\cong \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\cong \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B} & {\hookrightarrow} & \displaystyle \widetilde{\unicode[STIX]{x1D6FF}_{1}}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\cong \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\cong \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
Consequently,
and this representation is irreducible since
![]() $2x+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. Using Lemma 2.1 and [Reference Matić6, Theorem 4.6], we obtain that
$2x+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. Using Lemma 2.1 and [Reference Matić6, Theorem 4.6], we obtain that
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one and it follows that
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one and it follows that
![]() $\unicode[STIX]{x1D70B}$
appears in
$\unicode[STIX]{x1D70B}$
appears in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
If
![]() $x=a-1$
, in the similar way we obtain
$x=a-1$
, in the similar way we obtain
and
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
contains
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one. Thus, in this case
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one. Thus, in this case
![]() $\unicode[STIX]{x1D70B}$
again appears in
$\unicode[STIX]{x1D70B}$
again appears in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
Let us now consider the case
![]() $a<c$
. If
$a<c$
. If
![]() $(i,j)=(b,x)$
we obtain possible irreducible subquotient
$(i,j)=(b,x)$
we obtain possible irreducible subquotient
![]() $\unicode[STIX]{x1D70B}_{1}$
of
$\unicode[STIX]{x1D70B}_{1}$
of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
of the form
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
of the form
![]() $\unicode[STIX]{x1D70B}_{1}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})$
if
$\unicode[STIX]{x1D70B}_{1}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})$
if
![]() $x>c-1$
, and of the form
$x>c-1$
, and of the form
![]() $\unicode[STIX]{x1D70B}_{1}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
if
$\unicode[STIX]{x1D70B}_{1}\cong L(\widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
if
![]() $x=c-1$
(note that the segment
$x=c-1$
(note that the segment
![]() $[-x,-c]$
is contained in
$[-x,-c]$
is contained in
![]() $[-b,-a]$
).
$[-b,-a]$
).
It remains to examine the case
![]() $(i,j)=(x,b)$
. By Proposition 3.3, this case provides two possible irreducible subquotients
$(i,j)=(x,b)$
. By Proposition 3.3, this case provides two possible irreducible subquotients
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{3}$
of
$\unicode[STIX]{x1D70B}_{3}$
of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
:
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
:
![]() $\unicode[STIX]{x1D70B}_{2}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
and
$\unicode[STIX]{x1D70B}_{2}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
and
![]() $\unicode[STIX]{x1D70B}_{3}\cong \unicode[STIX]{x1D70B}_{1}$
. It can be proved in the same way as in the proof of Proposition 4.2 that both
$\unicode[STIX]{x1D70B}_{3}\cong \unicode[STIX]{x1D70B}_{1}$
. It can be proved in the same way as in the proof of Proposition 4.2 that both
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
appear in the composition series of
$\unicode[STIX]{x1D70B}_{2}$
appear in the composition series of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. What is still left is to show that these irreducible constituents appear with multiplicity one.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. What is still left is to show that these irreducible constituents appear with multiplicity one.
If
![]() $x>c-1$
, we denote by
$x>c-1$
, we denote by
![]() $2y^{\prime }+1=\min (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2b-1])$
. Now we have the following embeddings and isomorphisms:
$2y^{\prime }+1=\min (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2b-1])$
. Now we have the following embeddings and isomorphisms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{1} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-y^{\prime }-1}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{1} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-y^{\prime }-1}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}.\nonumber\end{eqnarray}$$
The induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])$
is obviously irreducible. Consequently, the irreducible representation
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])$
is obviously irreducible. Consequently, the irreducible representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
is contained in the Jacquet module of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
is contained in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{1}$
with respect to the appropriate parabolic subgroup
$\unicode[STIX]{x1D70B}_{1}$
with respect to the appropriate parabolic subgroup
![]() $P_{1}$
. Since
$P_{1}$
. Since
![]() $2y^{\prime }+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2y^{\prime }+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $a<c$
, from Lemma 2.1 and [Reference Matić6, Theorem 4.6] we deduce that the multiplicity of
$a<c$
, from Lemma 2.1 and [Reference Matić6, Theorem 4.6] we deduce that the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{y^{\prime }+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
![]() $r_{P_{1}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
$r_{P_{1}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y^{\prime }}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which equals one, since
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{y^{\prime }}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which equals one, since
![]() $y^{\prime }\leqslant x$
and
$y^{\prime }\leqslant x$
and
![]() $\unicode[STIX]{x1D70E}_{sp}$
is strongly positive.
$\unicode[STIX]{x1D70E}_{sp}$
is strongly positive.
If
![]() $x=c-1$
, since
$x=c-1$
, since
![]() $2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}^{(1)})$
, we have the following embeddings and isomorphisms:
$2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}^{(1)})$
, we have the following embeddings and isomorphisms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{1} & {\hookrightarrow} & \displaystyle \widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}{\hookrightarrow}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{1} & {\hookrightarrow} & \displaystyle \widetilde{\unicode[STIX]{x1D6FF}_{1}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}{\hookrightarrow}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}.\nonumber\end{eqnarray}$$
Thus,
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
is contained in the Jacquet module of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
is contained in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{2}$
with respect to the appropriate parabolic subgroup
$\unicode[STIX]{x1D70B}_{2}$
with respect to the appropriate parabolic subgroup
![]() $P_{2}$
. Since we have
$P_{2}$
. Since we have
![]() $2c-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2c-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $a<c$
, it is not hard to see, using Lemma 2.1 and [Reference Matić6, Theorem 4.6], that the multiplicity of
$a<c$
, it is not hard to see, using Lemma 2.1 and [Reference Matić6, Theorem 4.6], that the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
![]() $r_{P_{2}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
$r_{P_{2}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-c+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which equals one.
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which equals one.
It follows that
![]() $\unicode[STIX]{x1D70B}_{1}$
appears with multiplicity one in
$\unicode[STIX]{x1D70B}_{1}$
appears with multiplicity one in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
Representation
![]() $\unicode[STIX]{x1D70B}_{2}$
also appears with multiplicity one in
$\unicode[STIX]{x1D70B}_{2}$
also appears with multiplicity one in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
since Frobenius reciprocity shows that
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
since Frobenius reciprocity shows that
![]() $\widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
is contained in the Jacquet module of
$\widetilde{\unicode[STIX]{x1D6FF}_{2}}\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
is contained in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{2}$
with respect to the appropriate parabolic subgroup, and it can be seen using Lemma 2.1 that this irreducible representation appears with multiplicity one in the Jacquet module of
$\unicode[STIX]{x1D70B}_{2}$
with respect to the appropriate parabolic subgroup, and it can be seen using Lemma 2.1 that this irreducible representation appears with multiplicity one in the Jacquet module of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with respect to the appropriate parabolic subgroup. This ends the proof.◻
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with respect to the appropriate parabolic subgroup. This ends the proof.◻
Lemma 4.6. Suppose that
![]() $b<d$
,
$b<d$
,
![]() $x=y$
and
$x=y$
and
![]() $a\neq c$
. Let
$a\neq c$
. Let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
and
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
and
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. In
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. In
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)}).\nonumber\end{eqnarray}$$
Proof. Since
![]() $b<d$
,
$b<d$
,
![]() $x=y$
and
$x=y$
and
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible, it follows that
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
is irreducible, it follows that
![]() $c<a$
. Furthermore,
$c<a$
. Furthermore,
![]() $a\neq c$
provides
$a\neq c$
provides
![]() $x\geqslant c$
. In the same way as before, we deduce that the induced representation
$x\geqslant c$
. In the same way as before, we deduce that the induced representation
contains a strongly positive discrete series for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
if and only if
$c-1\leqslant j\leqslant d$
if and only if
![]() $(i,j)\in \{(b,d),(x,d),(b,x)\}$
.
$(i,j)\in \{(b,d),(x,d),(b,x)\}$
.
Let us first consider the case
![]() $x>a-1$
. The choice
$x>a-1$
. The choice
![]() $(i,j)=(b,d)$
provides the candidate
$(i,j)=(b,d)$
provides the candidate
![]() $\unicode[STIX]{x1D70B}_{1}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
for an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{1}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
for an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, the choice
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, the choice
![]() $(i,j)=(x,d)$
provides the candidate
$(i,j)=(x,d)$
provides the candidate
![]() $\unicode[STIX]{x1D70B}_{2}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
, while the choice
$\unicode[STIX]{x1D70B}_{2}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})$
, while the choice
![]() $(i,j)=(b,x)$
provides candidates
$(i,j)=(b,x)$
provides candidates
![]() $\unicode[STIX]{x1D70B}_{3}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
and
$\unicode[STIX]{x1D70B}_{3}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
and
![]() $\unicode[STIX]{x1D70B}_{4}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
. In the same way as before we see that
$\unicode[STIX]{x1D70B}_{4}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
. In the same way as before we see that
![]() $\unicode[STIX]{x1D70B}_{1}$
,
$\unicode[STIX]{x1D70B}_{1}$
,
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{3}$
are irreducible subquotients of
$\unicode[STIX]{x1D70B}_{3}$
are irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and each of them appears with multiplicity one. It remains to discuss
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and each of them appears with multiplicity one. It remains to discuss
![]() $\unicode[STIX]{x1D70B}_{4}$
.
$\unicode[STIX]{x1D70B}_{4}$
.
From
![]() $x<b$
and
$x<b$
and
![]() $c<a$
, we deduce that
$c<a$
, we deduce that
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])$
is irreducible, and
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])$
is irreducible, and
![]() $\unicode[STIX]{x1D70B}_{4}$
is the unique irreducible subrepresentation of
$\unicode[STIX]{x1D70B}_{4}$
is the unique irreducible subrepresentation of
and, consequently,
Since
![]() $x=y$
, the strongly positive discrete series
$x=y$
, the strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
is a subrepresentation of
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
is a subrepresentation of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
. It follows that
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
. It follows that
![]() $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
is an irreducible subrepresentation of the induced representation
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
is an irreducible subrepresentation of the induced representation
and, since
![]() $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}^{(1)})$
, [Reference Matić6, Theorem 4.6] can be used to determine that
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}^{(1)})$
, [Reference Matić6, Theorem 4.6] can be used to determine that
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
appears with multiplicity one in the Jacquet module of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
appears with multiplicity one in the Jacquet module of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
with respect to the appropriate parabolic subgroup. Thus,
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
with respect to the appropriate parabolic subgroup. Thus,
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
has the unique irreducible subrepresentation and we have
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}$
has the unique irreducible subrepresentation and we have
This implies
and
From (5) we get that
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
is contained in the Jacquet module of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
is contained in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup
$\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup
![]() $P_{1}$
. Using Lemma 2.1, together with
$P_{1}$
. Using Lemma 2.1, together with
![]() $x<b$
, we obtain that the multiplicity of
$x<b$
, we obtain that the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
![]() $r_{P_{1}}(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}))$
equals the multiplicity of
$r_{P_{1}}(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}))$
equals the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}))$
and it can be easily seen that this multiplicity equals one.
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}))$
and it can be easily seen that this multiplicity equals one.
The induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is obviously a subquotient of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
is obviously a subquotient of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
and it follows from the structural formula for
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
and it follows from the structural formula for
![]() $\unicode[STIX]{x1D707}^{\ast }$
that
$\unicode[STIX]{x1D707}^{\ast }$
that
![]() $r_{P_{1}}(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}))$
contains
$r_{P_{1}}(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)}))$
contains
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
. Consequently,
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
. Consequently,
and, by Lemma 3.4,
Using the definition of
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
we obtain the following embeddings and isomorphisms:
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
we obtain the following embeddings and isomorphisms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{4} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-x-1}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{4} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-x-1}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\nonumber\end{eqnarray}$$
Frobenius reciprocity shows that the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup
$\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup
![]() $P_{2}$
contains the irreducible representation
$P_{2}$
contains the irreducible representation
Since
![]() $2x+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, it follows that the multiplicity of
$2x+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, it follows that the multiplicity of
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $r_{P_{2}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
$r_{P_{2}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}$
in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which obviously equals one.
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which obviously equals one.
Thus,
![]() $\unicode[STIX]{x1D70B}_{4}$
appears in the composition series of the induced representation
$\unicode[STIX]{x1D70B}_{4}$
appears in the composition series of the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
Now we consider the case
![]() $x=a-1$
. The choice
$x=a-1$
. The choice
![]() $(i,j)=(b,d)$
provides the candidate
$(i,j)=(b,d)$
provides the candidate
![]() $\unicode[STIX]{x1D70B}_{5}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
for an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{5}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
for an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, the choice
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, the choice
![]() $(i,j)=(x,d)$
provides the candidate
$(i,j)=(x,d)$
provides the candidate
![]() $\unicode[STIX]{x1D70B}_{6}=L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
, while the choice
$\unicode[STIX]{x1D70B}_{6}=L(\widetilde{\unicode[STIX]{x1D6FF}_{2}}\rtimes \unicode[STIX]{x1D70E}_{sp}^{(1)})$
, while the choice
![]() $(i,j)=(b,x)$
provides candidates
$(i,j)=(b,x)$
provides candidates
![]() $\unicode[STIX]{x1D70B}_{7}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
and
$\unicode[STIX]{x1D70B}_{7}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
and
![]() $\unicode[STIX]{x1D70B}_{8}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
. Similarly as before, we deduce that
$\unicode[STIX]{x1D70B}_{8}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
. Similarly as before, we deduce that
![]() $\unicode[STIX]{x1D70B}_{5}$
,
$\unicode[STIX]{x1D70B}_{5}$
,
![]() $\unicode[STIX]{x1D70B}_{6}$
and
$\unicode[STIX]{x1D70B}_{6}$
and
![]() $\unicode[STIX]{x1D70B}_{7}$
are irreducible subquotients of
$\unicode[STIX]{x1D70B}_{7}$
are irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and each of them appears with the multiplicity one in the composition series. We discuss the representation
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and each of them appears with the multiplicity one in the composition series. We discuss the representation
![]() $\unicode[STIX]{x1D70B}_{8}$
. We have the following embeddings and isomorphisms:
$\unicode[STIX]{x1D70B}_{8}$
. We have the following embeddings and isomorphisms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{8} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}{\hookrightarrow}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-x-1}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{8} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}{\hookrightarrow}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-x-1}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}.\nonumber\end{eqnarray}$$
Thus,
![]() $\unicode[STIX]{x1D70B}_{8}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{8}$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
, and
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
, and
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
is contained in the Jacquet module of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
is contained in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{8}$
with respect to the appropriate parabolic subgroup
$\unicode[STIX]{x1D70B}_{8}$
with respect to the appropriate parabolic subgroup
![]() $P_{3}$
. Consequently, there is some irreducible subquotient
$P_{3}$
. Consequently, there is some irreducible subquotient
![]() $\unicode[STIX]{x1D70B}^{\prime \prime }$
of
$\unicode[STIX]{x1D70B}^{\prime \prime }$
of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
such that
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
such that
![]() $\unicode[STIX]{x1D70B}_{8}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70B}^{\prime \prime }$
. Since
$\unicode[STIX]{x1D70B}_{8}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70B}^{\prime \prime }$
. Since
![]() $2b+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}^{(2)})$
, using Lemma 2.1 and [Reference Matić6, Theorem 4.6] we get that
$2b+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp}^{(2)})$
, using Lemma 2.1 and [Reference Matić6, Theorem 4.6] we get that
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B}^{\prime \prime })\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
. Since
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B}^{\prime \prime })\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
. Since
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears with multiplicity one in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears with multiplicity one in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
and
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
and
![]() $\unicode[STIX]{x1D707}^{\ast }(L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}))\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
, we get
$\unicode[STIX]{x1D707}^{\ast }(L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}))\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
, we get
Lemma 3.4 now gives
Also, from
![]() $a>c$
and
$a>c$
and
![]() $2a-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, we deduce that multiplicity of
$2a-1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, we deduce that multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-a+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-a+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
![]() $r_{P_{3}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
$r_{P_{3}}(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
equals the multiplicity of
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-a+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-a+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
in
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which equals one. Consequently,
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
, which equals one. Consequently,
![]() $\unicode[STIX]{x1D70B}_{8}$
appears with multiplicity one in
$\unicode[STIX]{x1D70B}_{8}$
appears with multiplicity one in
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.◻
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.◻
The following lemma can be proved applying the same arguments as in the proof of Lemma 4.6, details being left to the reader.
Lemma 4.7. Suppose that
![]() $b<d$
,
$b<d$
,
![]() $x=y$
and
$x=y$
and
![]() $a=c$
. Let
$a=c$
. Let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
and
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
and
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. In
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. In
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)}).\nonumber\end{eqnarray}$$
5 The case of reducible
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
This section is devoted to description of the composition factors of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
when the induced representation
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
when the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
reduces. It follows that
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
reduces. It follows that
![]() $\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and, for simplicity of the notation, we write
$\unicode[STIX]{x1D70C}_{1}\cong \unicode[STIX]{x1D70C}_{2}$
and, for simplicity of the notation, we write
![]() $\unicode[STIX]{x1D70C}$
instead of
$\unicode[STIX]{x1D70C}$
instead of
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
. From
$\unicode[STIX]{x1D70C}_{2}$
. From
![]() $b\leqslant d$
and reducibility of
$b\leqslant d$
and reducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
we deduce
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}$
we deduce
![]() $a<c$
,
$a<c$
,
![]() $b<d$
and
$b<d$
and
![]() $c\leqslant b+1$
. Also, we have
$c\leqslant b+1$
. Also, we have
and note that, for
![]() $c\geqslant b$
, the composition factors of the induced representation
$c\geqslant b$
, the composition factors of the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
have been obtained in the previous section.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
have been obtained in the previous section.
Throughout this section, let
![]() $\unicode[STIX]{x1D6FF}_{3}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])$
and
$\unicode[STIX]{x1D6FF}_{3}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])$
and
![]() $\unicode[STIX]{x1D6FF}_{4}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])$
. Obviously,
$\unicode[STIX]{x1D6FF}_{4}=\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])$
. Obviously,
![]() $L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})$
is an irreducible subquotient of
$L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})$
is an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
If
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
, let
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
, let
![]() $2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
. Also, if
$2x+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1])$
. Also, if
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1]\neq \emptyset$
, let
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1]\neq \emptyset$
, let
![]() $2y+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1])$
.
$2y+1=\max (\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2c-1,2d-1])$
.
The following proposition can be proved applying the same arguments as in the proof of Proposition 4.2:
Proposition 5.1. Suppose that both representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are irreducible. In
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are irreducible. In
![]() $R(G)$
we have
$R(G)$
we have
Proposition 5.2. Suppose that representation
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and that
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces and that
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible. We denote by
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible. We denote by
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
and by
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
and by
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. If
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. If
![]() $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, in
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, in
![]() $R(G)$
we have
$R(G)$
we have
If
![]() $2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $x\geqslant c-1$
, in
$x\geqslant c-1$
, in
![]() $R(G)$
we have
$R(G)$
we have
If
![]() $2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $x<c-1$
, in
$x<c-1$
, in
![]() $R(G)$
we have
$R(G)$
we have
Proof. Let us determine all
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
, such that the induced representation
$c-1\leqslant j\leqslant d$
, such that the induced representation
contains a strongly positive discrete series. We consider the following possibilities:
-
∙
 $2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. Since
$2d+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. Since
 $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible, Lemma 3.4 implies
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible, Lemma 3.4 implies
 $x<c-1$
. Using Lemma 3.6, we deduce
$x<c-1$
. Using Lemma 3.6, we deduce
 $(i,j)\in \{(b,d),(x,d),(x,b)\}$
. The ordered pair
$(i,j)\in \{(b,d),(x,d),(x,b)\}$
. The ordered pair
 $(b,d)$
provides two possible irreducible subquotients, while each of other two ordered pairs provides one possible irreducible subquotient.
$(b,d)$
provides two possible irreducible subquotients, while each of other two ordered pairs provides one possible irreducible subquotient. -
∙
 $2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
 $x\geqslant c-1$
. In this case we have
$x\geqslant c-1$
. In this case we have
 $(i,j)\in \{(b,d),(x,d)\}$
and, since
$(i,j)\in \{(b,d),(x,d)\}$
and, since
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])$
reduces, Proposition 3.3 shows that in each case we have two possible irreducible subquotients.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])$
reduces, Proposition 3.3 shows that in each case we have two possible irreducible subquotients. -
∙
 $2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2d+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
 $x<c-1$
. Again, we have
$x<c-1$
. Again, we have
 $(i,j)\in \{(b,d),(x,d)\}$
and, since
$(i,j)\in \{(b,d),(x,d)\}$
and, since
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])$
is irreducible, Proposition 3.3 provides three possible irreducible subquotients.
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])$
is irreducible, Proposition 3.3 provides three possible irreducible subquotients.
Now the rest of the proof follows in the same way as in the proof of Proposition 4.2. ◻
Proposition 5.3. Suppose that the representation
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible and that
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
is irreducible and that
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces. We denote by
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduces. We denote by
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. If
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
. If
![]() $2b+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
or
$2b+1\not \in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
or
![]() $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $b<y$
, in
$b<y$
, in
![]() $R(G)$
we have
$R(G)$
we have
If
![]() $b=y$
and
$b=y$
and
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
, in
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
, in
![]() $R(G)$
we have
$R(G)$
we have
for strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
such that
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
.
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
.
If
![]() $b=y$
and
$b=y$
and
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]=\emptyset$
, in
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]=\emptyset$
, in
![]() $R(G)$
we have
$R(G)$
we have
Proof. We discuss only the case
![]() $2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
,
$2b+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
,
![]() $2b+1=y$
and
$2b+1=y$
and
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
. Other cases can be handled in the same way, but more easily.
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})\cap [2a-1,2b-1]\neq \emptyset$
. Other cases can be handled in the same way, but more easily.
In this case, the induced representation
contains a strongly positive discrete series for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
, if and only if
$c-1\leqslant j\leqslant d$
, if and only if
![]() $(i,j)\in \{(b,d),(b,b),(x,b)\}$
.
$(i,j)\in \{(b,d),(b,b),(x,b)\}$
.
For
![]() $(i,j)=(b,d)$
, we obtain candidates
$(i,j)=(b,d)$
, we obtain candidates
![]() $\unicode[STIX]{x1D70B}_{1}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
and
$\unicode[STIX]{x1D70B}_{1}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})$
and
![]() $\unicode[STIX]{x1D70B}_{2}=L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})$
for irreducible subquotients of
$\unicode[STIX]{x1D70B}_{2}=L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})$
for irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. For
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. For
![]() $(i,j)=(b,b)$
, we obtain a candidate
$(i,j)=(b,b)$
, we obtain a candidate
![]() $\unicode[STIX]{x1D70B}_{3}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})$
for an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{3}=L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})$
for an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and it can be shown in the same way as before that
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and it can be shown in the same way as before that
![]() $\unicode[STIX]{x1D70B}_{1}$
,
$\unicode[STIX]{x1D70B}_{1}$
,
![]() $\unicode[STIX]{x1D70B}_{2}$
and
$\unicode[STIX]{x1D70B}_{2}$
and
![]() $\unicode[STIX]{x1D70B}_{3}$
appear with multiplicity one in composition series of
$\unicode[STIX]{x1D70B}_{3}$
appear with multiplicity one in composition series of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
If
![]() $(i,j)=(x,b)$
and
$(i,j)=(x,b)$
and
![]() $c-1>x$
, using Proposition 3.3 we obtain a candidate
$c-1>x$
, using Proposition 3.3 we obtain a candidate
![]() $\unicode[STIX]{x1D70B}_{4}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
for irreducible subquotient of
$\unicode[STIX]{x1D70B}_{4}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
for irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
![]() $(i,j)=(x,b)$
and
$(i,j)=(x,b)$
and
![]() $c-1\leqslant x$
, then the induced representation
$c-1\leqslant x$
, then the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])$
reduces and in this case Proposition 3.3 provides, besides
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])$
reduces and in this case Proposition 3.3 provides, besides
![]() $\unicode[STIX]{x1D70B}_{4}$
, an additional candidate
$\unicode[STIX]{x1D70B}_{4}$
, an additional candidate
![]() $\unicode[STIX]{x1D70B}_{5}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
for irreducible subquotient of
$\unicode[STIX]{x1D70B}_{5}=L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
for irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
Let us prove that
![]() $\unicode[STIX]{x1D70B}_{4}$
is contained in the composition series of
$\unicode[STIX]{x1D70B}_{4}$
is contained in the composition series of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. We analyze several possibilities separately:
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. We analyze several possibilities separately:
-
∙
 $(x,b)=(a-1,c-1)$
. It follows directly from Lemma 3.6(c) that
$(x,b)=(a-1,c-1)$
. It follows directly from Lemma 3.6(c) that
 $\unicode[STIX]{x1D70B}_{4}\cong \unicode[STIX]{x1D70E}_{sp}^{(2)}$
is a subquotient of
$\unicode[STIX]{x1D70B}_{4}\cong \unicode[STIX]{x1D70E}_{sp}^{(2)}$
is a subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. -
∙
 $x>a-1$
and
$x>a-1$
and
 $b=c-1$
. Both representations
$b=c-1$
. Both representations
 $\unicode[STIX]{x1D70B}_{4}$
and
$\unicode[STIX]{x1D70B}_{4}$
and
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are contained in the induced representation (6)Since
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are contained in the induced representation (6)Since $$\begin{eqnarray}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\end{eqnarray}$$
 $x<c$
and
$x<c$
and
 $\unicode[STIX]{x1D70E}_{sp}$
is strongly positive, the structural formula for
$\unicode[STIX]{x1D70E}_{sp}$
is strongly positive, the structural formula for
 $\unicode[STIX]{x1D707}^{\ast }$
implies that the irreducible representation
$\unicode[STIX]{x1D707}^{\ast }$
implies that the irreducible representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears with multiplicity one in the Jacquet modules of induced representations
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears with multiplicity one in the Jacquet modules of induced representations
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and (6) with respect to the appropriate parabolic subgroup. By Frobenius reciprocity,
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and (6) with respect to the appropriate parabolic subgroup. By Frobenius reciprocity,
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears in the Jacquet module of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears in the Jacquet module of
 $\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup. Now Lemma 3.8 implies that
$\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup. Now Lemma 3.8 implies that
 $\unicode[STIX]{x1D70B}_{4}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{4}$
is an irreducible subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
-
∙
 $x=a-1$
and
$x=a-1$
and
 $b>c-1$
. In this case, both representations
$b>c-1$
. In this case, both representations
 $\unicode[STIX]{x1D70B}_{4}$
and
$\unicode[STIX]{x1D70B}_{4}$
and
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are contained in the induced representation (7)Since
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
are contained in the induced representation (7)Since $$\begin{eqnarray}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{b+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}.\end{eqnarray}$$
 $a<c$
and
$a<c$
and
 $\unicode[STIX]{x1D70E}_{sp}$
is strongly positive, it can be directly obtained that the irreducible representation
$\unicode[STIX]{x1D70E}_{sp}$
is strongly positive, it can be directly obtained that the irreducible representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears with multiplicity one in the Jacquet modules of induced representations
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70E}_{sp}^{(2)}$
appears with multiplicity one in the Jacquet modules of induced representations
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and (7) with respect to the appropriate parabolic subgroup. Since the same irreducible representation appears in the Jacquet module of
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and (7) with respect to the appropriate parabolic subgroup. Since the same irreducible representation appears in the Jacquet module of
 $\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup, Lemma 3.8 shows that
$\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup, Lemma 3.8 shows that
 $\unicode[STIX]{x1D70B}_{4}$
is an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{4}$
is an irreducible subquotient of
 $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
.
-
∙
 $x>a-1$
and
$x>a-1$
and
 $b>c-1$
. In the same way as in the proof of Lemma 4.6 we deduce that
$b>c-1$
. In the same way as in the proof of Lemma 4.6 we deduce that
 $\unicode[STIX]{x1D70B}_{4}$
is an irreducible subquotient of the induced representation
$\unicode[STIX]{x1D70B}_{4}$
is an irreducible subquotient of the induced representation
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
. Also, using the definition of
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
. Also, using the definition of
 $x$
and Lemma 3.4 we obtain that
$x$
and Lemma 3.4 we obtain that
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
is contained in
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})$
is contained in
 $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}$
, where
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}$
, where
 $\unicode[STIX]{x1D70E}_{sp}^{(3)}$
denotes the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(3)}$
denotes the strongly positive discrete series such that
 $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})\setminus \{(2b+1,\unicode[STIX]{x1D70C})\}\cup \{(2x+1,\unicode[STIX]{x1D70C})\}$
. Consequently, we have In
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})\setminus \{(2b+1,\unicode[STIX]{x1D70C})\}\cup \{(2x+1,\unicode[STIX]{x1D70C})\}$
. Consequently, we have In $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{4} & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{4} & {\leqslant} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}.\nonumber\end{eqnarray}$$
 $R(G)$
we have so there is
$R(G)$
we have so there is $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)} & = & \displaystyle L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)} & = & \displaystyle L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}),\nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}\in \{L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}),L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})\}$
such that
$\unicode[STIX]{x1D70B}\in \{L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}),L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)})\}$
such that
 $\unicode[STIX]{x1D70B}_{4}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70B}$
. Since
$\unicode[STIX]{x1D70B}_{4}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70B}$
. Since
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B}_{4})\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70B}^{\prime }$
for some irreducible representation
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B}_{4})\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70B}^{\prime }$
for some irreducible representation
 $\unicode[STIX]{x1D70B}^{\prime }$
, and
$\unicode[STIX]{x1D70B}^{\prime }$
, and
 $a<c$
, it follows that
$a<c$
, it follows that
 $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B})\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70B}^{\prime \prime }$
for some irreducible representation
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D70B})\geqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70B}^{\prime \prime }$
for some irreducible representation
 $\unicode[STIX]{x1D70B}^{\prime \prime }$
. Clearly, this leads to
$\unicode[STIX]{x1D70B}^{\prime \prime }$
. Clearly, this leads to
 $\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})$
.
$\unicode[STIX]{x1D70B}\cong L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})$
.
Using Lemma 3.4 we deduce
 $L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})\leqslant \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and we have
$L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})\leqslant \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, and we have  $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{4}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})\leqslant \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{4}\leqslant \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)})\leqslant \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}.\end{eqnarray}$$
It can be easily verified that the irreducible representation
appears in the Jacquet module of
![]() $\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup, and appears with multiplicity one in the Jacquet module of
$\unicode[STIX]{x1D70B}_{4}$
with respect to the appropriate parabolic subgroup, and appears with multiplicity one in the Jacquet module of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with respect to the same parabolic subgroup. Thus,
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with respect to the same parabolic subgroup. Thus,
![]() $\unicode[STIX]{x1D70B}_{4}$
appears in the composition series of
$\unicode[STIX]{x1D70B}_{4}$
appears in the composition series of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one.
In the rest of the proof we are concerned with representation
![]() $\unicode[STIX]{x1D70B}_{5}$
. Since
$\unicode[STIX]{x1D70B}_{5}$
. Since
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])$
is irreducible, using Lemma 3.4 we obtain the following embeddings and intertwining operators:
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])$
is irreducible, using Lemma 3.4 we obtain the following embeddings and intertwining operators:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{5} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{5} & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(2)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{a}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}^{(3)},\nonumber\end{eqnarray}$$
for strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}_{sp}^{(3)}$
such that
$\unicode[STIX]{x1D70E}_{sp}^{(3)}$
such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})\setminus \{(2b+1,\unicode[STIX]{x1D70C})\}\cup \{(2x+1,\unicode[STIX]{x1D70C})\}$
.
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})\setminus \{(2b+1,\unicode[STIX]{x1D70C})\}\cup \{(2x+1,\unicode[STIX]{x1D70C})\}$
.
Frobenius reciprocity and transitivity of Jacquet modules imply that there is an irreducible representation
![]() $\unicode[STIX]{x1D70B}$
such that
$\unicode[STIX]{x1D70B}$
such that
On the other hand, since
![]() $2x+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
$2x+1\in \text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
and
![]() $b<d$
, using Lemma 2.1 and [Reference Matić6, Theorem 4.6] we deduce that
$b<d$
, using Lemma 2.1 and [Reference Matić6, Theorem 4.6] we deduce that
![]() $\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
does not contain an irreducible constituent of the form
$\unicode[STIX]{x1D707}^{\ast }(\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp})$
does not contain an irreducible constituent of the form
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70B}$
. Consequently,
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{x+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\otimes \unicode[STIX]{x1D70B}$
. Consequently,
![]() $\unicode[STIX]{x1D70B}_{5}$
is not an irreducible subquotient of
$\unicode[STIX]{x1D70B}_{5}$
is not an irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and the proposition is proved.◻
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and the proposition is proved.◻
In the rest of this section we analyze the case when both induced representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduce. In what follows, let
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduce. In what follows, let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(1)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
, let
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(1)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C})\}$
, let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(2)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
, and let
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(2)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2y+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
, and let
![]() $\unicode[STIX]{x1D70E}_{sp}^{(3)}$
denote the strongly positive discrete series such that
$\unicode[STIX]{x1D70E}_{sp}^{(3)}$
denote the strongly positive discrete series such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}),(2y+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}),(2d+1,\unicode[STIX]{x1D70C})\}$
.
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(3)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C}),(2y+1,\unicode[STIX]{x1D70C})\}\cup \{(2b+1,\unicode[STIX]{x1D70C}),(2d+1,\unicode[STIX]{x1D70C})\}$
.
Note that if
![]() $x<y$
, then the reducibility of
$x<y$
, then the reducibility of
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
implies
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
implies
![]() $b<y$
.
$b<y$
.
Description of the composition factors of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
in the case when both induced representations
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
in the case when both induced representations
![]() $\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
$\unicode[STIX]{x1D6FF}_{1}\rtimes \unicode[STIX]{x1D70E}_{sp}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduce is divided in the following sequence of propositions.
$\unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
reduce is divided in the following sequence of propositions.
Proposition 5.4. Suppose that
![]() $x=y$
. Then in
$x=y$
. Then in
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)}).\nonumber\end{eqnarray}$$
Proof. The induced representation
contains a strongly positive discrete series for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
, if and only if
$c-1\leqslant j\leqslant d$
, if and only if
![]() $(i,j)\in \{(b,d),(x,d),(b,x),(x,b)\}$
. Since
$(i,j)\in \{(b,d),(x,d),(b,x),(x,b)\}$
. Since
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])$
is irreducible, ordered pair
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{c}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{x}\unicode[STIX]{x1D70C}])$
is irreducible, ordered pair
![]() $(i,j)=(b,x)$
provides one candidate for irreducible subquotient of
$(i,j)=(b,x)$
provides one candidate for irreducible subquotient of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, while all other choices provide two candidates. Also, the candidate
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
, while all other choices provide two candidates. Also, the candidate
![]() $L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
is provided by both choices
$L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})$
is provided by both choices
![]() $(i,j)=(b,x)$
and
$(i,j)=(b,x)$
and
![]() $(i,j)=(x,b)$
. The rest of the proof follows in the same way as before.◻
$(i,j)=(x,b)$
. The rest of the proof follows in the same way as before.◻
It remains to discuss the case
![]() $x<y$
. In this case, it is a direct consequence of Lemma 3.6 that the induced representation
$x<y$
. In this case, it is a direct consequence of Lemma 3.6 that the induced representation
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series subquotient if and only if
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series subquotient if and only if
![]() $x=a-1$
,
$x=a-1$
,
![]() $b=c-1$
and
$b=c-1$
and
![]() $x=y\_$
in
$x=y\_$
in
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. Furthermore, if
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
. Furthermore, if
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series subquotient, then the induced representation
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series subquotient, then the induced representation
contains a strongly positive discrete series subquotient for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
, if and only if
$c-1\leqslant j\leqslant d$
, if and only if
![]() $(i,j)\in \{(b,d),(x,d),(b,y),(x,y),(a,c)\}$
. On the other hand, if
$(i,j)\in \{(b,d),(x,d),(b,y),(x,y),(a,c)\}$
. On the other hand, if
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
does not contain a strongly positive discrete series subquotient, then the induced representation
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
does not contain a strongly positive discrete series subquotient, then the induced representation
![]() $\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series subquotient for
$\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{i+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{b}\unicode[STIX]{x1D70C}])\times \unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{j+1}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{d}\unicode[STIX]{x1D70C}])\rtimes \unicode[STIX]{x1D70E}_{sp}$
contains a strongly positive discrete series subquotient for
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $a-1\leqslant i\leqslant b$
,
$a-1\leqslant i\leqslant b$
,
![]() $c-1\leqslant j\leqslant d$
, if and only if
$c-1\leqslant j\leqslant d$
, if and only if
![]() $(i,j)\in \{(b,d),(x,d),(b,y),(x,y)\}$
.
$(i,j)\in \{(b,d),(x,d),(b,y),(x,y)\}$
.
Choices
![]() $(i,j)=(b,d)$
and
$(i,j)=(b,d)$
and
![]() $(i,j)=(b,y)$
provide two possible irreducible subquotients of
$(i,j)=(b,y)$
provide two possible irreducible subquotients of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
. If
![]() $x\geqslant c-1$
, the choices
$x\geqslant c-1$
, the choices
![]() $(i,j)=(x,d)$
and
$(i,j)=(x,d)$
and
![]() $(i,j)=(x,y)$
also provide two possible irreducible subquotients, otherwise each of those choices provides one possible irreducible subquotient. It can be seen in the same way as before that each obtained irreducible representation appears in the composition series of
$(i,j)=(x,y)$
also provide two possible irreducible subquotients, otherwise each of those choices provides one possible irreducible subquotient. It can be seen in the same way as before that each obtained irreducible representation appears in the composition series of
![]() $\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one, that is, we have the following results:
$\unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp}$
with multiplicity one, that is, we have the following results:
Proposition 5.5. Suppose that
![]() $x<y$
and
$x<y$
and
![]() $x\geqslant c-1$
. Then in
$x\geqslant c-1$
. Then in
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-d}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)}).\nonumber\end{eqnarray}$$
Proposition 5.6. Suppose that
![]() $x<y$
and
$x<y$
and
![]() $x<c-1$
. If
$x<c-1$
. If
![]() $x=a-1$
,
$x=a-1$
,
![]() $b=c-1$
and
$b=c-1$
and
![]() $x=y\_$
in
$x=y\_$
in
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, then in
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, then in
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)})+\unicode[STIX]{x1D70E}_{sp}^{(4)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)})+\unicode[STIX]{x1D70E}_{sp}^{(4)},\nonumber\end{eqnarray}$$
for the strongly positive discrete series
![]() $\unicode[STIX]{x1D70E}_{sp}^{(4)}$
such that
$\unicode[STIX]{x1D70E}_{sp}^{(4)}$
such that
![]() $\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(4)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
.
$\text{Jord}(\unicode[STIX]{x1D70E}_{sp}^{(4)})=\text{Jord}(\unicode[STIX]{x1D70E}_{sp})\setminus \{(2x+1,\unicode[STIX]{x1D70C})\}\cup \{(2d+1,\unicode[STIX]{x1D70C})\}$
.
Proposition 5.7. Suppose that
![]() $x<y$
and
$x<y$
and
![]() $x<c-1$
. If either
$x<c-1$
. If either
![]() $x>a-1$
, or
$x>a-1$
, or
![]() $b>c-1$
or
$b>c-1$
or
![]() $x<y\_$
in
$x<y\_$
in
![]() $\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, in
$\text{Jord}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D70E}_{sp})$
, in
![]() $R(G)$
we have
$R(G)$
we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{1}\times \unicode[STIX]{x1D6FF}_{2}\rtimes \unicode[STIX]{x1D70E}_{sp} & = & \displaystyle L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}_{3},\unicode[STIX]{x1D6FF}_{4},\unicode[STIX]{x1D70E}_{sp})+L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\widetilde{\unicode[STIX]{x1D6FF}_{2}},\unicode[STIX]{x1D70E}_{sp}^{(1)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\widetilde{\unicode[STIX]{x1D6FF}_{1}},\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-b}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(2)})\nonumber\\ \displaystyle & & \displaystyle +\,L(\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-x}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-a}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D6FF}([\unicode[STIX]{x1D708}^{-y}\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}^{-c}\unicode[STIX]{x1D70C}]),\unicode[STIX]{x1D70E}_{sp}^{(3)}).\nonumber\end{eqnarray}$$
Acknowledgments
The author would like to thank the referee for a number of corrections and very useful suggestions.