Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-12T04:18:52.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete conformal metrics with prescribed scalar curvature on subdomains of a compact manifold

Published online by Cambridge University Press:  22 January 2016

Shin Kato  and
Shin Nayatani
Shin Kato
Affiliation:
Department of Mathematics, Nara Women’s University, Nara 630, Japan
Shin Nayatani
Affiliation:
Mathematical Institute, Tohoku University, Sendai 980, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (M, g) be a Riemannian manifold of dimension n≥ 3 and ĝanother metric on M which is pointwise conformai to g. It can be written 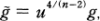where u is a positive smooth function on M. Then the curvature of g is computable in terms of that of g and the derivatives of u up to second order. In particular, if S and S denote the scalar curvature of g and g respectively, they are related by the equation

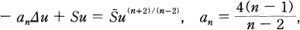
where ▽u denotes the Laplacian of u, defined with respect to the metric g.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 132 , December 1993 , pp. 155 - 173
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

References

[1] Aubin, T., Nonlinear analysis on manifolds Monge-Ampère equations, Springer, New York, 1982.Google Scholar
[2] Aviles, P. and McOwen, R. C., Complete conformal metrics with negative scalar curvature in compact Riemannian manifolds, Duke Math. J., 56 (1988), 395–398.CrossRefGoogle Scholar
[3] Brezis, H. and Kamin, S., Sublinear elliptic equations in Rn , Manuscripta Math., 74 (1992), 87–106.Google Scholar
[4] Fischer-Colbrie, D. and Schoen, R., The structure of complete stable minimal surfaces in 3-manifolds of non-negative scalar curvature, Comm. Pure Appl. Math., 33 (1980), 199–211.CrossRefGoogle Scholar
[5] Gidas, B., Ni, W.-M. and Nirenberg, L., Symmetry and related properties via the maximum principle, Comm. Math. Phys., 68 (1979), 209–243.Google Scholar
[6] Gidas, B. and Spruck, J., Global and local behavior of positive solutions of non-linear elliptic equations, Comm. Pure Appl. Math., 34 (1981), 525–598.Google Scholar
[7] Jin, Z., A counterexample to the Yamabe problem for complete noncompact manifolds, Partial Differential Equations (Lecture Notes in Math. 1306) ed. by Chern, S. S., Springer, Berlin, 1988,93–101.Google Scholar
[8] Kato, S., Conformai deformation to prescribed scalar curvature on complete non-compact Riemannian manifolds with nonpositive curvature, Tôhoku Math. J., 45 (1993), 205–230.Google Scholar
[9] Kazdan, J. and Warner, F., Scalar curvature and conformal deformation of Riemannian structurel. Differential Geom., 10 (1975), 113–134.Google Scholar
[10] Li, Y. and Ni, W.-M., On conformai scalar curvature equations in Rn , Duke Math. J., 57 (1988), 895–924.Google Scholar
[11] Loewner, C. and Nirenberg, L., Partial differential equations invariant under conformal and projective transformations, Contributions to Analysis, Academic Press, New York, 1974,245–272.Google Scholar
[12] Lee, J. M. and Parker, T. H., The Yamabe problem, Bull. Amer. Math. Soc, 17 (1987), 37–91.CrossRefGoogle Scholar
[13] Ma, X. and McOwen, R. C., The Laplacian on complete manifolds with warped cylindrical ends, Comm. Partial Differential Equations, 16 (1991), 1583–1614.Google Scholar
[14] Mazzeo, R. and Smale, N., Conformally flat metrics of constant positive scalar curvature on subdomains of the sphere, J. Differential Geom., 34 (1991), 581–621.Google Scholar
[15] Naito, M., A note on bounded positive entire solutions of semilinear equations, Hiroshima Math. J., 14 (1984), 211–214.Google Scholar
[16] Ni, W. M., On the elliptic equation Δu + K(x)u(n+2)/n-2 = 0, its generalizations, and applications in geometry, Indiana Univ. Math. J., 31 (1982), 493–529.Google Scholar
[17] Nicholls, P. J., The ergodic theory of discrete groups, Cambridge University Press, Cambridge, 1989.Google Scholar
[18] Schoen, R., Conformal deformation of a Riemannian metric to constant scalar curvature, J. Differential Geom., 20 (1984), 479–495.CrossRefGoogle Scholar
[19] Schoen, R., The existence of weak solutions with prescribed singular behavior for a conformally invariant scalar equation, Comm. Pure Appl. Math., 41 (1988), 317–392.CrossRefGoogle Scholar
[20] Schoen, R., A report on some recent progress on nonlinear problems in geometry, Surveys in Differential Geom., 1 (1991), 201–241.Google Scholar
[21] Schoen, R. and Yau, S.-T., Conformally flat manifolds, Kleinian groups and scalar curvature, Invent. Math., 92 (1988), 47–71.Google Scholar
[22] Delanoe, P., Generalized stereographic projections with prescribed scalar curvature, Contemporary Math., 127 (1992), 17–25.Google Scholar