Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-22T22:09:05.847Z Has data issue: false hasContentIssue false
  • English
  • Français

A COMPARISON OF CATEGORICAL AND TOPOLOGICAL ENTROPIES ON WEINSTEIN MANIFOLDS

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  17 February 2025

HANWOOL BAE Open the ORCID record for HANWOOL BAE [Opens in a new window]  and
SANGJIN LEE Open the ORCID record for SANGJIN LEE [Opens in a new window]
HANWOOL BAE
Affiliation:
Center for Quantum Structures in Modules and Spaces Seoul National University Seoul, South Korea [email protected]
SANGJIN LEE*
Affiliation:
Center for Geometry and Physics Institute for Basic Science (IBS) Pohang 37673, Korea [email protected]
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let W be a symplectic manifold, and let 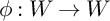$\phi :W \to W$ be a symplectic automorphism. This automorphism induces an auto-equivalence 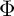$\Phi $ defined on the Fukaya category of W. In this paper, we prove that the categorical entropy of 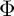$\Phi $ provides a lower bound for the topological entropy of 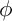$\phi $, where W is a Weinstein manifold and 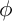$\phi $ is compactly supported. Furthermore, motivated by [cCGG24], we propose a conjecture that generalizes the result of [New88, Prz80, Yom87].

Keywords

categorical entropytopological entropysymplectic automorphism

MSC classification

Primary: 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Secondary: 53D40: Floer homology and cohomology, symplectic aspects
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, M. R. R., Colin, V. and Honda, K., Topological entropy for Reeb vector fields in dimension three via open book decompositions , J. Éc. polytech. Math. 6 (2019), 119–148. MR 3915194CrossRefGoogle Scholar
Adler, R. L., Konheim, A. G. and McAndrew, M. H., Topological entropy , Trans. Amer. Math. Soc. 114 (1965), 309–319. MR 175106CrossRefGoogle Scholar
Alves, M. R. R., Cylindrical contact homology and topological entropy , Geom. Topol. 20 (2016), no. 6, 3519–3569. MR 3590356CrossRefGoogle Scholar
Alves, M. R. R. and Meiwes, M., Dynamically exotic contact spheres in dimensions $\ge 7$ , Comment. Math. Helv. 94 (2019), no. 3, 569–622. MR 4014780CrossRefGoogle Scholar
Alves, M. R. R. and Meiwes, M., Braid stability and the Hofer metric , Ann. H. Lebesgue 7 (2024), 521–581. MR 4799904CrossRefGoogle Scholar
Arnol’d, V. I., Dynamics of complexity of intersections , Bol. Soc. Brasil. Mat. (N.S.) 21 (1990), no. 1, 1–10. MR 1139553CrossRefGoogle Scholar
Arnol’d, V. I., Dynamics of intersections, analysis, et cetera , Academic Press, Boston, MA, 1990, pp. 77–84. MR 1039340CrossRefGoogle Scholar
Abouzaid, M. and Smith, I., Exact Lagrangians in plumbings , Geom. Funct. Anal. 22 (2012), no. 4, 785–831. MR 2984118CrossRefGoogle Scholar
Bae, H., Choa, D., Jeong, W., Karabas, D. and Lee, S., On Categorical Entropy from the viewpoint of Symplectic Topology, arXiv preprint, arXiv:2203.12205, 2022.Google Scholar
Bae, H. and Lee, S., Pseudo-anosov autoquivalances arising from symplectic topology and their hyperbolic actions on stability conditions, arXiv preprint v1, arXiv:2311.07339, 2023.Google Scholar
Bowen, R., Entropy for group endomorphisms and homogeneous spaces , Trans. Amer. Math. Soc. 153 (1971), 401–414.CrossRefGoogle Scholar
Brin, M. and Stuck, G. J., Introduction to dynamical systems, corrected paper back edition of the 2002 original [MR1963683], Cambridge Univ. Press, Cambridge, 2015. MR3558919Google Scholar
Cineli, E., Ginzburg, V. L. and Gürel, B. Z., Topological entropy of Hamiltonian diffeomorphisms: A persistence homology and Floer theory perspective , Math. Z. 308 (2024), no. 4, Paper No. 73, 38. MR 4822772CrossRefGoogle Scholar
Chantraine, B., Rizell, G. D., Ghiggini, P. and Golovko, R., Geometric generation of the wrapped Fukaya category of Weinstein manifolds and sectors , Ann. Sci. Éc. Norm. Supér. (4) 57 (2024), no. 1, 1–85. MR 4732675Google Scholar
Cieliebak, K. and Eliashberg, Y. M., From Stein to Weinstein and back, American Mathematical Society Colloquium Publications, 59, Amer. Math. Soc., Providence, RI, 2012. MR3012475CrossRefGoogle Scholar
Dahinden, L., Lower complexity bounds for positive contactomorphisms , Israel J. Math. 224 (2018), no. 1, 367–383. MR 3799760CrossRefGoogle Scholar
Dahinden, L., Positive topological entropy of positive contactomorphisms , J. Symplectic Geom. 18 (2020), no. 3, 691–732. MR 4142484CrossRefGoogle Scholar
Dimitrov, G., Haiden, F., Katzarkov, L. and Kontsevich, M., “Dynamical systems and categories” in The influence of Solomon Lefschetz in geometry and topology, Contemporary Mathematics, 621, edited by L. Katzarkov, E. Lupercio, F. J. Turrubiates, American Mathematical Society, Providence, RI, 2014, pp. 133–170. MR 3289326Google Scholar
Dinaburg, E. I., The relation between topological entropy and metric entropy , Soviet Math. Dok 11 (1970), 13–16.Google Scholar
Dinaburg, E. I., On the relations among various entropy characteristics of dynamical systems , Math. USSR-Izvestiya 5 (1971), 337.CrossRefGoogle Scholar
Drinfeld, V., DG quotients of DG categories , J. Algebra 272 (2004), no. 2, 643–691. MR 2028075CrossRefGoogle Scholar
Ehresmann, C., “Les connexions infinitésimales dans un espace fibré différentiable” in Séminaire Bourbaki, Vol. 1, Exp. No. 24, 153–168, Soc. Math. France, Paris, MR1605161Google Scholar
Fel’shtyn, A. The growth rate of symplectic Floer homology , J. Fixed Point Theory Appl. 12 (2012), nos. 1–2, 93–119. MR 3034856CrossRefGoogle Scholar
Farb, B. and Margalit, D., A primer on mapping class groups, Princeton Mathematical Series, 49, Princeton University Press, Princeton, NJ, 2012. MR 2850125Google Scholar
Frauenfelder, U. and Schlenk, F., Volume growth in the component of the Dehn-Seidel twist , Geom. Funct. Anal. 15 (2005), no. 4, 809–838. MR 2221151CrossRefGoogle Scholar
Frauenfelder, U. and Schlenk, F., Fiberwise volume growth via Lagrangian intersections , J. Symplectic Geom. 4 (2006), no. 2, 117–148. MR 2275001CrossRefGoogle Scholar
Gelfand, S. I. and Manin, Y. I., Methods of homological algebra, second edition, Springer Monographs in Mathematics, Springer, Berlin, 2003. MR1950475CrossRefGoogle Scholar
Giroux, E. and Pardon, J., Existence of Lefschetz fibrations on Stein and Weinstein domains , Geom. Topol. 21 (2017), no. 2, 963–997. MR 3626595CrossRefGoogle Scholar
Ganatra, S., Pardon, J. and Shende, V., Sectorial descent for wrapped Fukaya categories , J. Amer. Math. Soc. 37 (2024), no. 2, 499–635. MR 4695507Google Scholar
Gromov, M., Entropy, homology and semialgebraic geometry, 1987, 145–146, Séminaire Bourbaki, Vol. 1985/86, pp. 5, 225–240. MR 880035Google Scholar
Gong, W., Wang, Z. W. and Xue, J., Dynamics of composite symplectic dehn twists, arXiv preprint, arXiv:2208.13041, 2022.Google Scholar
Hofer, J. E., Topological entropy for noncompact spaces and other extensions. Ph.D. thesis, ProQuest LLC, Ann Arbor, MI, 1972, Oregon State University. MR 2621482Google Scholar
Hofer, J. E., Topological entropy for noncompact spaces , Michigan Math. J. 21 (1974), 235–242. MR 370542Google Scholar
Katok, A. B. and Hasselblatt, B., Introduction to the modern theory of dynamical systems, Encyclopedia of Mathematics and its Applications, 54, Cambridge Univ. Press, Cambridge, 1995. MR1326374CrossRefGoogle Scholar
Kikuta, K. and Ouchi, G., Hochschild entropy and categorical entropy, Arnold Math J. (2023), no. 2, 223–244. MR4601969Google Scholar
Kislev, A. and Shelukhin, E., Bounds on spectral norms and barcodes , Geom. Topol. 25 (2021), no. 7, 3257–3350. MR 4372632CrossRefGoogle Scholar
Lee, S., Towards a higher-dimensional construction of stable/unstable Lagrangian laminations , Geom. Topol. 24 (2024), no. 2, 655–716. MR 4735043CrossRefGoogle Scholar
Mattei, D., Categorical vs topological entropy of autoequivalences of surfaces , Mosc. Math. J. 21 (2021), no. 2, 401–412. MR 4252457CrossRefGoogle Scholar
Macarini, L. and Schlenk, F., Positive topological entropy of Reeb flows on spherizations , Math. Proc. Cambridge Philos. Soc. 151 (2011), no. 1, 103–128. MR 2801317CrossRefGoogle Scholar
Newhouse, S. E., Entropy and volume , Ergod. Theory Dyn. Syst. 8 ${}^{\ast }$ (1988), no. Charles Conley Memorial Issue, 283–299. MR 967642Google Scholar
Penner, R. C., A construction of pseudo-Anosov homeomorphisms , Trans. Amer. Math. Soc. 310 (1988), no. 1, 179–197. MR 930079CrossRefGoogle Scholar
Polterovich, L., Rosen, D., Samvelyan, K. and Zhang, J., Topological persistence in geometry and analysis, University Lecture Series, 74, American Mathematical Society, Providence, RI, 2020. MR 4249570CrossRefGoogle Scholar
Przytycki, F., An upper estimation for topological entropy of diffeomorphisms , Invent. Math. 59 (1980), no. 3, 205–213. MR 579699CrossRefGoogle Scholar
Robinson, C., Dynamical systems, second edition, Studies in Advanced Mathematics, CRC, Boca Raton, FL, 1999; MR1792240Google Scholar
Seidel, P., Fukaya categories and Picard–Lefschetz theory, Zurich Lectures in Advanced Mathamatics, European Mathematical Society, Zürich, 2008.CrossRefGoogle Scholar
Smith, I., Floer cohomology and pencils of quadrics , Invent. Math. 189 (2012), no. 1, 149–250. MR 2929086CrossRefGoogle Scholar
Sylvan, Z., On partially wrapped fukaya categories , J. Topol. 12 (2019), no. 2, 372–441.CrossRefGoogle Scholar
Usher, M. and Zhang, J., Persistent homology and Floer-Novikov theory , Geom. Topol. 20 (2016), no. 6, 3333–3430. MR 3590354CrossRefGoogle Scholar
Weinstein, A., Symplectic manifolds and their Lagrangian submanifolds , Adv. Math. 6 (1971), 329–346. MR 286137CrossRefGoogle Scholar
Yomdin, Y., Volume growth and entropy , Israel J. Math. 57 (1987), no. 3, 285–300. MR 889979CrossRefGoogle Scholar