COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE 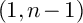$(1,n-1)$

Abstract

In their renowned paper (2011, Inventiones Mathematicae 184, 591–627), I. Vollaard and T. Wedhorn defined a stratification on the special fiber of the unitary unramified PEL Rapoport–Zink space with signature 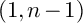$(1,n-1)$ . They constructed an isomorphism between the closure of a stratum, called a closed Bruhat–Tits stratum, and a Deligne–Lusztig variety which is not of classical type. In this paper, we describe the 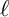$\ell $ -adic cohomology groups over 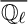$\overline {{\mathbb Q}_{\ell }}$ of these Deligne–Lusztig varieties, where 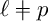$\ell \not = p$ . The computations involve the spectral sequence associated with the Ekedahl–Oort stratification of a closed Bruhat–Tits stratum, which translates into a stratification by Coxeter varieties whose cohomology is known. Eventually, we find out that the irreducible representations of the finite unitary group which appear inside the cohomology contribute to only two different unipotent Harish-Chandra series, one of them belonging to the principal series.

Introduction

Rapoport–Zink spaces are geometric objects which can be seen as deformation spaces for a p-divisible group equipped with additional structures. They are formal schemes over the ring of integers of a p-adic field, and they are constructed by means of a moduli problem which grants them with commuting actions from some p-adic and Galois groups. Therefore, the étale cohomology of these spaces carries representations of these groups simultaneously, and it is expected to realize a local version of the Langlands correspondence. Computing this cohomology is an arduous problem in general. So far, it has only been entirely described in a few special cases such as the Lubin–Tate tower or the Drinfeld space; in particular, both of them correspond to Rapoport–Zink spaces of EL type.

The difficulty in studying the cohomology of the Rapoport–Zink spaces is maybe reflected by the lack of precise understanding of their geometry in general. However, for some specific choices of the set of data, the resulting moduli space may display some nice geometric properties, giving hopes that their cohomology could be accessible. It is the case of the unitary unramified PEL (Polarization, Endomorphism, Level structure) Rapoport–Zink space ${\mathcal M}$ of signature $(1,n-1)$ , whose special fiber ${\mathcal M}_{\mathrm {red}}$ is described by the Bruhat–Tits stratification constructed by Vollaard and Wedhorn in a series of two papers [14] and [15]. This stratification $\{{\mathcal M}_{\Lambda }\}_{\Lambda }$ has two interesting features. On the one hand, the closed strata ${\mathcal M}_{\Lambda }$ are indexed by the set of vertices $\Lambda $ of the Bruhat–Tits building of a p-adic group of unitary similitudes J defined by the PEL data. On the other hand, each individual closed stratum ${\mathcal M}_{\Lambda }$ is isomorphic to a Deligne–Lusztig variety. They usually show up in Deligne–Lusztig theory, whose aim is the classification of the irreducible representations of finite groups of Lie type. In particular, the cohomology of these varieties has been extensively studied in the past decades. In a series of two papers, we aim at exploiting these geometric observations in order to link the cohomology theories of Deligne–Lusztig varieties and of Rapoport–Zink spaces.

Our strategy in order to examine the cohomology of the Rapoport–Zink space ${\mathcal M}$ takes place in two steps: first, we compute the cohomology groups $\mathrm {H}^{\bullet }_{c}({\mathcal M}_{\Lambda },\overline {{\mathbb Q}_{\ell }})$ (with $\ell \not = p$ ) of the closed strata; second, we use the combinatorics of the Bruhat–Tits building to get information on the cohomology of ${\mathcal M}$ . More precisely, in the second stage, we introduce the analytical generic fiber ${\mathcal M}^{\mathrm {an}}$ . It is covered by the analytical tubes $U_{\Lambda }$ of the closed strata ${\mathcal M}_{\Lambda }$ . These are open subdomains of ${\mathcal M}^{\mathrm {an}}$ whose cohomology coincides with the cohomology of the closed strata up to a suitable Tate twist and shift in degrees. Through the Čech spectral sequence associated with the open cover $\{U_{\Lambda }\}_{\Lambda }$ , we prove the semisimplicity of the Frobenius action on ${\mathrm H}^{\bullet }_c({\mathcal M}^{\mathrm {an}},\overline {{\mathbb Q}_{\ell }})$ , and we determine the cuspidal supports of its irreducible subquotients as a smooth representation of the group of unitary similitudes J. It also turns out that these cohomology groups are not J-admissible in general. Lastly, the p-adic uniformization theorem relates the Rapoport–Zink space ${\mathcal M}^{\mathrm {an}}$ with the basic stratum of an associated PEL unitary Shimura variety through a geometric isomorphism. It induces a Hochschild–Serre-type spectral sequence on the cohomology, through which we compute the individual cohomology groups of the basic stratum in the case $n=3$ and $4$ . In particular, we find out that some automorphic representations occur with a multiplicity depending on p which is a completely new phenomenon.

In the present paper, we carry out the first step of the strategy described above, namely we compute the cohomology of the individual closed Bruhat–Tits strata by exploiting Deligne–Lusztig theory. The second step and the results stated above can be found in the sequel [13].

Let q be a power of the prime number p. Let ${\mathbf G}$ be a connected reductive group over an algebraic closure ${\mathbb F}$ of ${\mathbb F}_{q}$ . Assume that ${\mathbf G}$ is equipped with an ${\mathbb F}_q$ -structure induced by a Frobenius morphism $F: {\mathbf G} \rightarrow {\mathbf G}$ . For ${\mathbf P}$ a parabolic subgroup of ${\mathbf G}$ , the associated generalized parabolic Deligne–Lusztig variety is defined by

$$ \begin{align*} X_{{\mathbf P}} := \{g{\mathbf P} \in {\mathbf G}/{\mathbf P} \,|\, g^{-1}F(g) \in {\mathbf P} F({\mathbf P})\}. \end{align*} $$

Usually, parabolic Deligne–Lusztig varieties have been studied with the additional assumption that ${\mathbf P}$ contains a Levi complement $\mathbf L$ such that $F(\mathbf L) = \mathbf L$ . Indeed, they are used to define the Deligne–Lusztig induction and restriction functors between the categories of representations of $\mathbf L^F$ and of ${\mathbf G}^F$ (see, e.g., [3]). However, the closed Bruhat–Tits strata constructed by Vollaard and Wedhorn are isomorphic to Deligne–Lusztig varieties $X_{{\mathbf P}}$ associated with parabolic subgroups ${\mathbf P}$ which do not satisfy this assumption. We call them generalized, and to the best of our knowledge, their cohomology has not been studied so far.

The closed Bruhat–Tits strata ${\mathcal M}_{\Lambda }$ are isomorphic to generalized Deligne–Lusztig varieties $X_I(\mathrm {id})$ associated with finite unitary groups $\mathrm {U}_{2d+1}(p)$ in an odd number of variables. Although only the case $q = p$ is relevant in the context of Vollaard and Wedhorn’s paper [15], we will work in this paper with a general q. In [15], the authors defined yet another stratification on each individual stratum. It is called the Ekedahl–Oort stratification, and it gives a decomposition $X_I(\mathrm {id}) \simeq \bigsqcup _{0\leq t\leq d} X_{I_t}(w_t)$ into locally closed subvarieties. It turns out that each Ekedahl–Oort stratum $X_{I_t}(w_t)$ is isomorphic to a Deligne–Lusztig variety which is not generalized. Moreover, they are closely related to Coxeter varieties whose cohomology is known thanks to the work of Lusztig in [10]. The Ekedahl–Oort stratification on $X_I(\mathrm {id})$ induces a spectral sequence on the cohomology, through which we are able to entirely compute the individual cohomology groups in terms of representations of ${\mathrm U}_{2d+1}(q)$ . The representations which occur are all unipotent, and these are classified by partitions of $2d+1$ or equivalently by Young diagrams (see [5], [12]). Given a partition $\lambda = (\lambda _1 \geq \cdots \geq \lambda _r)$ of $2d+1$ with $\lambda _r> 0$ , the associated irreducible unipotent representation of $\mathrm {U}_{2d+1}(q)$ is denoted by $\rho _{\lambda }$ . We may now state our main result, whose proof covers Section 5 of the paper. In the statement, the prime number $\ell $ is different from p, the field ${\mathbb F}$ is an algebraic closure of ${\mathbb F}_{q}$ , and $\mathrm {Frob}$ is the geometric Frobenius relative to ${\mathbb F}_{q^2}$ acting on the cohomology groups.

Theorem. The following statements hold.

1. (1) The cohomology group ${\mathrm H}_c^i(X_I(\mathrm {id}) \otimes {\mathbb F},\overline {{\mathbb Q}_{\ell }})$ is zero unless $0 \leq i \leq 2d$ . There is an isomorphism ${\mathrm H}_c^i(X_I(\mathrm {id})\otimes {\mathbb F},\overline {{\mathbb Q}_{\ell }}) \simeq {\mathrm H}_c^{2d-i}(X_I(\mathrm {id}) \otimes {\mathbb F},\overline {{\mathbb Q}_{\ell }})^{\vee }(d)$ which is equivariant for the actions of $\mathrm {Frob}$ and of ${\mathrm U}_{2d+1}(q)$ .

2. (2) The Frobenius element $\mathrm {Frob}$ acts like multiplication by $(-q)^i$ on ${\mathrm H}_c^i(X_I(\mathrm {id}) \otimes {\mathbb F},\overline {{\mathbb Q}_{\ell }})$ .

3. (3) For $0\leq i \leq d$ , we have

   $$ \begin{align*} {\mathrm H}_c^{2i}(X_I(\mathrm{id}) \otimes {\mathbb F},\overline{{\mathbb Q}_{\ell}}) = \bigoplus_{s=0}^{\min(i,d - i)} \rho_{(2d + 1 - 2s, 2s)}. \end{align*} $$

4. (4) For $0\leq i \leq d - 1$ , we have

   $$ \begin{align*} {\mathrm H}_c^{2i+1}(X_I(\mathrm{id}) \otimes {\mathbb F},\overline{{\mathbb Q}_{\ell}}) = \bigoplus_{s=0}^{\min(i,d - 1 - i)} \rho_{(2d - 2s, 2s + 1)}. \end{align*} $$

In particular, when the index is even, all the representations in the cohomology groups contribute to the unipotent principal series, but when the index is odd, the representations belong to the unipotent series determined by a minimal Levi complement of $\mathrm {U}_{2d+1}(q)$ which is not a torus.

Notations. Throughout the paper, we fix q a power of an odd prime number p. If k is a perfect field extension of ${\mathbb F}_q$ , we denote by $\sigma : x \mapsto x^q$ the qth power Frobenius of $\mathrm {Gal}(k/{\mathbb F}_q)$ . We fix an algebraic closure ${\mathbb F}$ of ${\mathbb F}_q$ . Unless specified otherwise, ${\mathbf G}$ will denote a connected reductive group over ${\mathbb F}$ equipped with an ${\mathbb F}_q$ -structure, induced by a Frobenius morphism $F: {\mathbf G} \rightarrow {\mathbf G}$ . If $\mathbf H$ is an F-stable subgroup of ${\mathbf G}$ , we denote by $H := \mathbf H^F \simeq \mathbf H({\mathbb F}_q)$ its group of ${\mathbb F}_q$ -rational points. We fix a pair $(\mathbf T,\mathbf B)$ consisting of a maximal torus $\mathbf T$ contained in a Borel subgroup $\mathbf B$ , both of them being F-stable. Such a pair always exists up to $G={\mathbf G}^F$ -conjugation. We obtain a Coxeter system $({\mathbf W},{\mathbf S})$ on which F acts, where ${\mathbf W} = {\mathbf W}(\mathbf T)$ is the Weyl group attached to $\mathbf T$ and ${\mathbf S}$ is the set of simple reflexions. It can be identified with the Weyl group of ${\mathbf G}$ as defined in [2]. Let $\ell $ denote the length function on ${\mathbf W}$ relative to ${\mathbf S}$ . For $I\subset {\mathbf S}$ , we write ${\mathbf P}_I, {\mathbf U}_I, \mathbf L_I$ , respectively, for the standard parabolic subgroup of type I, for its unipotent radical, and for its unique Levi complement containing $\mathbf T$ . We also write ${\mathbf W}_I$ for the parabolic subgroup of ${\mathbf W}$ generated by the simple reflexions in I. Recall that an element $w\in {\mathbf W}$ is said to be I-reduced (resp. reduced-I) if for every $v\in {\mathbf W}_I$ , we have $\ell (vw) = \ell (v) + \ell (w)$ (resp. $\ell (wv) = \ell (w) + \ell (v)$ ). The set of I-reduced (resp. reduced-I) elements is denoted by ${}^I{\mathbf W}$ (resp. ${\mathbf W}^{I}$ ). If $I,I'\subset {\mathbf S}$ , an element is said to be I-reduced- $I'$ if it belongs to ${}^I{\mathbf W}^{I'} := {}^I{\mathbf W} \cap {\mathbf W}^{I'}$ .

1 The generalized Deligne–Lusztig variety $X_I(\mathrm {id})$

We recall the definition of Deligne–Lusztig varieties from [1]. If ${\mathbf P}$ is any parabolic subgroup of ${\mathbf G}$ , the associated generalized parabolic Deligne–Lusztig variety is

$$ \begin{align*}X_{{\mathbf P}} := \{g{\mathbf P}\in {\mathbf G}/{\mathbf P}\,|\,g^{-1}F(g)\in {\mathbf P} F({\mathbf P})\}.\end{align*} $$

When these varieties were first introduced in [2], only the case of Borel subgroups was considered, hence the adjective parabolic. Moreover, parabolic Deligne–Lusztig varieties have mostly been studied with the additional assumption that ${\mathbf P}$ contains an F-stable Levi complement (see, e.g., [3]). This is not required by the definition above, hence the adjective generalized. Using the Coxeter system as above, one may give an equivalent description of these varieties. For $I,I'\subset {\mathbf S}$ , the generalized Bruhat decomposition is an isomorphism

$$ \begin{align*}{\mathbf P}_I\backslash {\mathbf G} / {\mathbf P}_{I'} = \bigsqcup_{w\in{}^I{\mathbf W}^{I'}} {\mathbf P}_I\backslash {\mathbf P}_Iw{\mathbf P}_{I'}/{\mathbf P}_{I'} \simeq {\mathbf W}_{I}\backslash {\mathbf W} / {\mathbf W}_{I'}.\end{align*} $$

For $w\in {}^I{\mathbf W}^{F(I)}$ , the generalized parabolic Deligne–Lusztig varieties is defined by

$$ \begin{align*}X_I(w) = \{g{\mathbf P}_I\in {\mathbf G}/{\mathbf P}_I \,|\, g^{-1}F(g)\in {\mathbf P}_IwF({\mathbf P}_I)\}.\end{align*} $$

The families of varieties $X_{{\mathbf P}}$ and $X_I(w)$ are the same, and [1] explains how to go from one description to the other. The case $I = \emptyset $ corresponds to usual Deligne–Lusztig varieties in ${\mathbf G}/\mathbf B$ . Moreover, the additional assumption regarding the existence of a rational Levi complement translates into the equation

(*) $$ \begin{align} w^{-1}Iw = F(I), \end{align} $$

which is a compatibility condition between the parameters w and I. The variety $X_I(w)$ is defined over ${\mathbb F}_{q^{\iota }}$ , where $\iota $ is the least integer such that $F^{\iota }(I) = I$ and $F^{\iota }(w) = w$ .

Proposition 1. For $I\subset {\mathbf S}$ and $w\in {}^I{\mathbf W}^{F(I)}$ , we have

$$ \begin{align*}\dim X_I(w) = \ell(w) + \dim {\mathbf G}/{\mathbf P}_{I\cap wF(I)w^{-1}} - \dim {\mathbf G}/{\mathbf P}_{I}.\end{align*} $$

Let us introduce a few more notations. If $I,I' \subset {\mathbf S}$ , the generalized Bruhat decomposition implies that the ${\mathbf G}$ -orbits for the diagonal action on ${\mathbf G}/{\mathbf P}_I \times {\mathbf G}/{\mathbf P}_{I'}$ are given by

$$ \begin{align*} \mathcal O_{I,I'}(w) := \{(g{\mathbf P}_I,h{\mathbf P}_{I'}) \,|\, g^{-1}h \in {\mathbf P}_Iw{\mathbf P}_{I'}\} \end{align*} $$

for $w\in {}^I{\mathbf W}^{I'}$ . The Deligne–Lusztig variety $X_I(w)$ can be seen as the intersection of $\mathcal O_{I,F(I)}(w)$ with the graph of the Frobenius $F:{\mathbf G}/{\mathbf P}_I \rightarrow {\mathbf G}/{\mathbf P}_{F(I)}$ . This intersection is transverse (see [2, Lem. 9.11], the proof deals with the case $I = \emptyset $ , but it generalizes to any I.) Thus, the proposition is a consequence of the following lemma and the fact that $\dim {\mathbf P}_I = \dim {\mathbf P}_{F(I)}$ .

Lemma 2. For $I,I' \subset {\mathbf S}$ and $w\in {}^I{\mathbf W}^{I'}$ , we have

$$ \begin{align*} \dim \mathcal O_{I,I'}(w) = \ell(w) + \dim {\mathbf G}/{\mathbf P}_{I\cap wI'w^{-1}}. \end{align*} $$

Proof. Recall that for $I \subset {\mathbf S}$ , the standard parabolic subgroup of type I decomposes as a union of Bruhat cells ${\mathbf P}_I = \mathbf B{\mathbf W}_I\mathbf B$ , and any Bruhat cell $\mathbf Bw\mathbf B$ has dimension $\dim \mathbf B + \ell (w)$ . Therefore, $\dim {\mathbf P}_I = \dim \mathbf B + \ell (I)$ where $\ell (I)$ denotes the maximal length of elements of ${\mathbf W}_I$ . Let $I,I'$ and w be as in the lemma. Consider the first projection $\mathcal O_{I,I'}(w) \rightarrow {\mathbf G}/{\mathbf P}_I$ , which is a surjective morphism with fibers isomorphic to ${\mathbf P}_Iw{\mathbf P}_{I'}/{\mathbf P}_{I'}$ . It is flat since ${\mathbf G} \rightarrow {\mathbf G}/{\mathbf P}_I$ is faithfully flat, and the pullback $\mathcal O_{I,I'}(w) \times _{{\mathbf G}/{\mathbf P}_I} {\mathbf G}$ is isomorphic to ${\mathbf G} \times {\mathbf P}_Iw{\mathbf P}_{I'}/{\mathbf P}_{I'}$ , which is flat over ${\mathbf G}$ . We have

$$ \begin{align*} {\mathbf P}_Iw{\mathbf P}_{I'} = \mathbf B{\mathbf W}_I\mathbf Bw\mathbf B{\mathbf W}_{I'}\mathbf B = \mathbf B {\mathbf W}_Iw{\mathbf W}_{I'}\mathbf B; \end{align*} $$

therefore, the dimension of a fiber is given by

$$ \begin{align*} \dim {\mathbf P}_Iw{\mathbf P}_{I'}/{\mathbf P}_{I'} = \dim {\mathbf P}_Iw{\mathbf P}_{I'} - \dim {\mathbf P}_{I'} = \max_{v\in {\mathbf W}_Iw{\mathbf W}_{I'}} \ell(v) - \ell(I'). \end{align*} $$

Since w is I-reduced- $I'$ , according to [4, Lem. 3.2.2], any element $v \in W_Iw{\mathbf W}_{I'}$ can uniquely be written as $v = xwy$ such that $x\in {\mathbf W}_I, y \in {\mathbf W}_{I'}$ and $xw$ is reduced- $I'$ . In particular, $\ell (v) = \ell (x) + \ell (w) + \ell (y)$ . It follows that

$$ \begin{align*} \max_{v\in {\mathbf W}_Iw{\mathbf W}_{I'}} \ell(v) = \ell(w) + \max_{x \in {\mathbf W}_I \cap {\mathbf W}^{I'}w^{-1}} \ell(x) + \ell(I'). \end{align*} $$

We prove that ${\mathbf W}_I \cap {\mathbf W}^{I'}w^{-1} = {\mathbf W}_I \cap {\mathbf W}^{I\cap wI'w^{-1}}$ .

Let $x \in {\mathbf W}_I \cap {\mathbf W}^{I'}w^{-1}$ , and we show that x is reduced- $(I\cap wI'w^{-1})$ . Let $s \in I\cap wI'w^{-1}$ , so that we can write $s = wtw^{-1}$ for some $t\in I'$ . Then $xsw = xwt$ . Since $xs \in {\mathbf W}_I$ and w is I-reduced, the left-hand side has length $\ell (xs) + \ell (w)$ . On the other hand, since $t\in I'$ and $xw$ is reduced- $I'$ , the right-hand side has length $\ell (xw) + 1 = \ell (x) + \ell (w) + 1$ . Therefore, $\ell (xs) = \ell (x) + 1$ as expected.

For the other inclusion, let $y \in {\mathbf W}_I \cap {\mathbf W}^{I\cap wI'w^{-1}}$ . We show that $yw$ is reduced- $I'$ . Toward a contradiction, assume that $\ell (ywt) < \ell (yw)$ for some $t\in I'$ . Let $y = s_1\ldots s_r$ and $w = u_1\ldots u_{r'}$ be reduced expressions, respectively, of y and of w, with the $s_i$ in I and the $u_j$ in ${\mathbf S}$ . Since w is I-reduced, the concatenation of both reduced expressions give a reduced expression of $yw$ . By the exchange condition (see [4, Th. 2.1.2]), we have

$$ \begin{align*}ywt = s_1 \ldots \widehat{s_i}\ldots s_r w \text { or } yu_1\ldots \widehat{u_j}\ldots u_{r'}\end{align*} $$

for some $1\leq i \leq r$ or $1\leq j \leq r'$ , where $\widehat {\cdot }$ denotes the product with one omitted term. The second case is impossible, since after simplifying y it would contradict the fact that w is reduced- $I'$ . Let us write $s := y^{-1}s_1 \ldots \widehat {s_i}\ldots s_r \in {\mathbf W}_I$ , so that we have $wt = sw$ . The left-hand side has length $\ell (w) + 1$ , and the right-hand side has length $\ell (s) + \ell (w)$ . It follows that $s\in I$ has length $1$ . Therefore, $s = wtw^{-1} \in I\cap wI'w^{-1}$ . Eventually, we have $\ell (ys) = \ell (y) + 1$ since y is reduced- $(I\cap wI'w^{-1})$ . This is absurd, because $ys = s_1 \ldots \widehat {s_i}\ldots s_r$ has length $r-1 = \ell (y)-1$ .

To conclude the proof, we recall the following general fact. If $({\mathbf W},{\mathbf S})$ is a Coxeter system and $K \subset {\mathbf S}$ , then the product map ${\mathbf W}^K \times {\mathbf W}_K \xrightarrow {\sim } {\mathbf W}$ sending $(w^K,w_K)$ to $w^Kw_K$ is a bijection. In particular, we have

$$ \begin{align*} \max_{w\in {\mathbf W}} \ell(w) = \max_{w^K \in {\mathbf W}^K} \ell(w^K) + \max_{w_K \in {\mathbf W}_K} \ell(w_K). \end{align*} $$

We apply this to the Coxeter system $({\mathbf W}_I,I)$ and $K = I\cap wI'w^{-1}$ . It follows that

$$ \begin{align*} \max_{x \in {\mathbf W}_I \cap {\mathbf W}^{I'}w^{-1}} \ell(x) = \max_{x \in {\mathbf W}_I \cap {\mathbf W}^{I\cap wI'w^{-1}}} \ell(x) = \ell(I) - \ell(I\cap wI'w^{-1}). \end{align*} $$

Putting things together, we have proved that

$$ \begin{align*} \dim \mathcal O_{I,I'}(w) & = \dim {\mathbf G}/{\mathbf P}_I + \dim {\mathbf P}_Iw{\mathbf P}_{I'}/{\mathbf P}_{I'} \\ & = \dim {\mathbf G} - \dim \mathbf B - \ell(I) + \max_{v\in {\mathbf W}_Iw{\mathbf W}_{I'}} \ell(v) - \ell(I') \\ & = \dim {\mathbf G} - \dim \mathbf B - \ell(I) + \ell(w) + \max_{x \in {\mathbf W}_I \cap {\mathbf W}^{I'}w^{-1}} \ell(x) \\ & = \dim {\mathbf G} - \dim \mathbf B - \ell(I\cap wI'w^{-1}) + \ell(w)\\ & = \dim {\mathbf G}/{\mathbf P}_{I\cap wI'w^{-1}} + \ell(w).\\[-36pt] \end{align*} $$

Remark 3. In [15, §4.4], the formula given by the authors for the dimension of $\mathcal O_{I,I'}(w)$ , and as a consequence for the Deligne–Lusztig variety $X_I(w)$ as well, contained a mistake.

Let d be a nonnegative integer, and let V be a $(2d+1)$ -dimensional ${\mathbb F}_{q^2}$ -vector space. Let $(\cdot ,\cdot ):V\times V \to {\mathbb F}_{q^2}$ be a nondegenerate Hermitian form on V. This Hermitian structure on V is unique up to isomorphism. In particular, we may once and for all fix a basis $\mathcal B$ of V in which $(\cdot ,\cdot )$ is described by the square matrix $\dot {w}_0$ of size $2d +1$ , having $1$ on the anti-diagonal and $0$ everywhere else. If k is a perfect field extension of ${\mathbb F}_{q^2}$ , we may extend the pairing to $V_k := V\otimes _{{\mathbb F}_{q^2}} k$ by setting

$$ \begin{align*}(v\otimes x,w\otimes y):=xy^{\sigma}(v,w)\in k\end{align*} $$

for all $v,w\in V$ and $x,y\in k$ . If U is a subspace of $V_k$ , we denote by $U^{\perp }$ its orthogonal, which is the subspace of all vectors $x\in V_k$ such that $(x,U)=0$ . Let J denote the finite group of Lie type $\mathrm {U}(V,(\cdot ,\cdot ))$ . It is defined as the group of F-fixed points of $\mathbf J := \mathrm {GL}(V)_{{\mathbb F}}$ with F a nonsplit Frobenius morphism. Using the basis $\mathcal B$ , the group $\mathbf J$ is identified with $\mathrm {GL}_{2d+1}$ with ${\mathbb F}_q$ -structure induced by the Frobenius morphism $F(M):=\dot {w}_0(M^{(q)})^{-t}\dot {w}_0$ , where $M^{(q)}$ denotes the matrix M having all coefficients raised to the power q. We may then identify J with the usual finite unitary group $\mathrm {U}_{2d+1}(q)$ . The pair $(\mathbf T,\mathbf B)$ consisting of the maximal torus of diagonal matrices and the Borel subgroup of upper-triangular matrices is F-stable. The Weyl system of $(\mathbf T,\mathbf B)$ may be identified with $(\mathfrak S_{2d+1},{\mathbf S})$ in the usual manner, where ${\mathbf S}$ is the set of simple transpositions $s_i:=(i\quad i+1)$ for $1\leq i \leq 2d$ . Under this identification, the Frobenius acts on ${\mathbf W}$ as the conjugation by the element $w_0$ , characterized for having the maximal length. It satisfies $w_0(i) = 2d + 2 -i$ , and a natural representative of $w_0$ in the normalizer of $\mathbf T$ is no other than $\dot {w}_0$ . Since $w_0$ has order $2$ , the action of the Frobenius on ${\mathbf W}$ is involutive. It also preserves the simple reflexions with the formula $F(s_i) = s_{2d+1-i}$ . We define the following subset of ${\mathbf S}$ :

$$ \begin{align*}I:=\{s_1,\ldots ,s_{d} ,s_{d+2},\ldots ,s_{2d}\} = {\mathbf S}\setminus \{s_{d+1}\}.\end{align*} $$

We have $F(I) = {\mathbf S} \setminus \{s_{d}\} \not = I$ . We consider the generalized Deligne–Lusztig variety $X_{I}(\mathrm {id})$ . It corresponds to the variety denoted $Y_{\Lambda }$ in [15, §4.5]. It has dimension d, and it does not satisfy the compatibility condition (*). According to [15, Lem. 4.5], we have the following.

Proposition 4. The variety $X_{I}(\mathrm {id})$ is defined over ${\mathbb F}_{q^2}$ , and it is projective, smooth, geometrically irreducible of dimension d.

Although the proposition in [15] is only stated in the case $q = p$ , the arguments carry over to general q. The geometric irreducibility is a consequence of the criterion proved in [1].

Remark 5. As mentioned above, the dimension formula for generalized Deligne–Lusztig varieties in [15] contains a mistake. For example, we may consider the Deligne–Lusztig variety $X_I(s_2s_1)$ for $\mathrm {U}_{3}({\mathbb F}_q)$ with $I = \{s_1\}$ . It satisfies (*) so that $\dim X_I(s_2s_1) = \ell (s_2s_1) = 2$ according to [3]. However, we have ${\mathbf P}_{I\cap F(I)} = \mathbf B$ and $\dim {\mathbf G}/\mathbf B = 3$ , whereas $\dim {\mathbf G}/{\mathbf P}_I = 2$ , so that the formula of [15] says that $X_I(s_2s_1)$ would be of dimension $2+3-2 = 3$ .

Nonetheless, the formula of [15] does give the correct result in the case of $X_I(\mathrm {id})$ . It is because for $w = \mathrm {id}$ , we have $I\cap wF(I)w^{-1} = I \cap F(I)$ . Therefore, the validity of the authors’ work is not affected in any way.

Rational points of Deligne–Lusztig varieties associated with a unitary group $\mathrm {U}$ over ${\mathbb F}_q$ can be described in terms of vectorial flags, in a certain relative position with respect to their image by the Frobenius. Let k be a perfect field extension of ${\mathbb F}_{q^2}$ . According to [14, Lem. 2.12], the Frobenius acts on a flag $\mathcal F$ in $V_k$ by sending it to its orthogonal flag $\mathcal F^{\perp }$ . Explicitly, we have

Here, given our choice of I, a k-rational point of $X_I(\mathrm {id})$ corresponds to a flag of the type

$$ \begin{align*}\mathcal F: \{0\} \subset U \subset V_k\end{align*} $$

with U having dimension $d+1$ , and which is of relative position $\mathrm {id}$ with respect to $\mathcal F^{\perp }$ . This precisely means that U must contain $U^{\perp }$ .

Proposition 6. The k-rational points of $X_I(\mathrm {id})$ are given by

$$ \begin{align*}X_I(\mathrm{id})(k) \simeq \{U\subset V_k \,|\, \dim U = d+1 \text{ and }U^{\perp}\subset U\}.\end{align*} $$

In [15, §5.3], the authors defined the Ekedahl–Oort stratification on the Deligne–Lusztig variety $X_I(\mathrm {id})$ . By [15, Cor. 5.12], it turns out that each stratum is itself isomorphic to a Deligne–Lusztig variety which is not generalized. For $0 \leq t \leq d$ , we define the subset

$$ \begin{align*}I_{t}:=\{s_1,\ldots ,s_{d - t -1},s_{d + t + 2},\ldots ,s_{2d}\} \subset {\mathbf S}.\end{align*} $$

It consists of all $2d$ simple reflexions in ${\mathbf S}$ , except that we removed the $2t+2$ ones in the middle. Thus, it has cardinality $2(d - t - 1)$ . In particular, it is empty for $t = d$ or $d-1$ . We also define the cycle $w_{t} := (d + t + 1 \quad d + t \, \ldots \, d +1)$ . Its decomposition into simple reflexions is $w_{t} = s_{d+1}\ldots s_{d + t}$ . When $t = 0$ , it is the identity. We note that even though $I_{d} = I_{d-1} = \emptyset $ , we still have $w_{d} \not = w_{d-1}$ . One may check that $F(I_{t}) = I_{t}$ and that $w_{t}$ belongs to $^{I_{t}}{\mathbf W}^{I_{t}}$ . Moreover, the compatibility condition (*) is satisfied for the pair $(I_{t},w_{t})$ . Indeed, the reduced decomposition for $w_{t}$ does not use any simple reflexion that is adjacent to those in $I_{t}$ . By [15, §3.3 and §5.3], we have the following result.

Proposition 7. The Deligne–Lusztig variety $X_{I_t}(w_t)$ is defined over ${\mathbb F}_{q^2}$ and has dimension t. There is a natural immersion $X_{I_t}(w_t) \hookrightarrow X_I(\mathrm {id})$ inducing a stratification

$$ \begin{align*}X_I(\mathrm{id}) = \bigsqcup_{0 \leq t \leq d} X_{I_t}(w_t).\end{align*} $$

The closure of the stratum $X_{I_t}(w_t)$ is the union of all the strata $X_{I_s}(w_s)$ for $s \leq t$ .

Following the proof of Theorem 2.15 of [14], we can describe the stratification at the level of rational points. Let k be a perfect field extension of ${\mathbb F}_{q^2}$ . By the choice of $I_{t}$ , a k-point of $X_{I_{t}}(w_{t})$ is a flag

with $\dim (\mathcal F_{-i}) = d+1-i$ and $\dim (\mathcal F_i) = d+i$ for $1\leq i \leq t +1$ , and which is in relative position $w_t$ with respect to $\mathcal F^{\perp }$ . It means that we have a diagram of the following type.

Here, $\tau := \sigma ^2\cdot \mathrm {id}$ is an ${\mathbb F}_{q^2}$ -linear automorphism of $V_k$ , and it satisfies $\tau (U) = (U^{\perp })^{\perp }$ for every subspace $U \subset (V_{\Lambda })_k$ . This diagram implies that $\tau (\mathcal F_i) = \mathcal F_{i-1} + \tau (\mathcal F_{i-1})$ for all $2\leq i \leq t+1$ . This rewrites as $\mathcal F_{i} = \mathcal F_{i-1} + \tau ^{-1}(\mathcal F_{i-1})$ . We deduce that

$$ \begin{align*}\mathcal F_i = \sum_{l=0}^{i-1} \tau^{-l}(\mathcal F_1)\end{align*} $$

for all $1\leq i \leq t+1$ . Thus, the whole flag is determined by the subspace $\mathcal F_1$ , which has dimension $d+1$ and contains its orthogonal. The immersion $X_{I_t}(w_t) \hookrightarrow X_I(\mathrm {id})$ maps the flag $\mathcal F$ to $\mathcal F_1$ .

Conversely, a k-point of $X_I(\mathrm {id})$ is given by a subspace $U \subset V_k$ of dimension $d+1$ containing its orthogonal. For $i \geq 1$ , we define

$$ \begin{align*}\mathcal F_i := \sum_{l=0}^{i-1} \tau^{-1}(U) \subset V_k.\end{align*} $$

Then $(\mathcal F_i)_{i\geq 1}$ is a nondecreasing sequence of subspaces of $V_k$ . Let t be the smallest integer such that $\mathcal F_{t+1} = \mathcal F_{t+2}$ . It follows that $0 \leq t \leq d$ and that t is also the smallest integer such that $\mathcal F_{t+1} = \tau (\mathcal F_{t+1})$ . Moreover, the orthogonal $U^{\perp }$ has dimension d, and we have $U^{\perp } \subset U$ , so that $U^{\perp } \subset (U^{\perp })^{\perp } = \tau (U)$ . In particular, if $t>0$ , then $U \cap \tau (U) = U^{\perp }$ . Thus, we have $\dim (\mathcal F_2) = d + 2$ . Similarly, we have $\dim (\mathcal F_i) = d+i$ for all $1 \leq i \leq t+1$ . By setting $\mathcal F_{-i} := \mathcal F_i^{\perp }$ , we obtain a flag $\mathcal F$ that is the k-rational point of $X_{I_t}(w_t)$ associated with U.

The Deligne–Lusztig varieties $X_{I_{t}}(w_{t})$ are related to Coxeter varieties for smaller unitary groups as we now explain. We define

$$ \begin{align*}K_{t} := \{s_1,\ldots s_{d-t-1}, s_{d-t+1},\ldots , s_{d+t}, s_{d+t+2}, \ldots , s_{2d}\} = {\mathbf S} \setminus \{s_{d-t}, s_{d+t+1}\}.\end{align*} $$

The set $K_{t}$ is obtained from $I_{t}$ by adding the $2t$ simple reflexions in the middle. It has cardinality $2d - 2$ and satisfies $F(K_{t}) = K_{t}$ . We have $I_{t} \subset K_{t}$ with equality if and only if $t=0$ .

Proposition 8. There is a ${\mathrm U}_{2d+1}(q)$ -equivariant isomorphism

$$ \begin{align*}X_{I_{t}}(w_{t}) \simeq {\mathrm U}_{2d+1}(q)/U_{K_{t}} \times_{L_{K_{t}}} X_{I_{t}}^{\mathbf L_{K_{t}}}(w_{t}),\end{align*} $$

where $X_{I_{t}}^{\mathbf L_{K_{t}}}(w_{t})$ is a Deligne–Lusztig variety for $\mathbf L_{K_{t}}$ . The zero-dimensional variety ${\mathrm U}_{2d+1}(q)/U_{K_{t}}$ has a left action of ${\mathrm U}_{2d+1}(q)$ and a right action of $L_{K_{t}}$ .

Proof. This is an application of [3, Prop. 7.19], which is the geometric identity behind the transitivity of the Deligne–Lusztig functors. It applies to the varieties $X_{I_t}(w_t)$ because they satisfy the compatibility condition (*), as well as the following conditions: $K_{t}$ contains $I_{t}$ , it is stable by the Frobenius, and $w_{t}$ belongs to the parabolic subgroup ${\mathbf W}_{K_{t}} \simeq \mathfrak S_{d-t}\times \mathfrak S_{2t+1} \times \mathfrak S_{d-t} \subset \mathfrak S_{2d +1}$ .

The Levi complement $\mathbf L_{K_{t}}$ is isomorphic to the product $\mathrm {GL}_{d-t} \times \mathrm {GL}_{2t +1} \times \mathrm {GL}_{d - t}$ as a reductive group over ${\mathbb F}$ . Given a matrix $M = \mathrm {diag}(A,C,B) \in \mathbf L_{K_{t}}$ , we have $F(M) = \mathrm {diag}(F(B),F(C),F(A))$ , where we still denote by F the Frobenius morphism for smaller linear groups. Writing $\mathbf H$ for the product of the two $\mathrm {GL}_{d-t}$ factors, we have $\mathbf L_{K_{t}} \simeq \mathbf H \times \mathrm {GL}_{2t +1}$ and both factors inherit an ${\mathbb F}_q$ -structure by means of F. We have $L_{K_{t}} \simeq \mathrm {GL}_{d-t}(q^2) \times {\mathrm U}_{2t +1}(q)$ , the first factor corresponding to H. The Weyl group of $\mathbf L_{K_{t}}$ is isomorphic to ${\mathbf W}_{\mathbf H}\times \mathfrak S_{2t +1}$ where ${\mathbf W}_{\mathbf H} \simeq \mathfrak S_{d-t}\times \mathfrak S_{d-t}$ is the Weyl group of $\mathbf H$ . Via this decomposition, the permutation $w_{t}$ corresponds to $\mathrm {id}\times \widetilde {w_{t}}$ , where $\widetilde {w_{t}}$ is the restriction of $w_{t}$ to $\{d - t + 1, \ldots , d + t + 1\}$ . Similarly, the set of simple reflexions ${\mathbf S}$ decomposes as ${\mathbf S}_{\mathbf H}\sqcup \widetilde {{\mathbf S}}$ , the second term corresponding to the simple reflexions in $\mathfrak S_{2t+1}$ . Then, we have $I_{t} = {\mathbf S}_{\mathbf H} \sqcup \emptyset $ . The Deligne–Lusztig variety for $\mathbf L_{K_{t}}$ decomposes accordingly as the following product:

$$ \begin{align*}X_{I_{t}}^{\mathbf L_{K_{t}}}(w_{t}) = X_{{\mathbf S}_{\mathbf H}}^{\mathbf H}(\mathrm{id}) \times X_{\emptyset}^{{\mathrm U}_{2t+1}(q)}(\widetilde{w_{t}}).\end{align*} $$

The variety $X_{{\mathbf S}_{\mathbf H}}^{\mathbf H}(\mathrm {id})$ is just a point, whereas $X_{\emptyset }^{{\mathrm U}_{2t+1}(q)}(\widetilde {w_{t}})$ is a Deligne–Lusztig variety for the unitary group of size $2t +1$ . We observe that the permutation $\widetilde {w_{t}}$ is a Coxeter element in $\mathfrak S_{2t+1}$ , that is, the product of exactly one simple reflexion for each orbit of the Frobenius. Deligne–Lusztig varieties attached to Coxeter elements are called Coxeter varieties, and their cohomology with coefficients in $\overline {{\mathbb Q}_{\ell }}$ where $\ell $ is a prime number different from p are well understood thanks to the work of Lusztig in [10]. Before stating his results, we recall parts of the representation theory of finite unitary groups.

2 Irreducible unipotent representations of the finite unitary group

In this section, we recall the classification of the irreducible unipotent representations of the finite unitary group and we explain the underlying combinatorics. For $w\in {\mathbf W}$ , let $\dot {w}$ be a representative of w in the normalizer $\mathrm N_{{\mathbf G}}(\mathbf T)$ of $\mathbf T$ . By the Lang-Steinberg theorem, one can find $g\in {\mathbf G}$ such that $\dot {w} = g^{-1}F(g)$ . Then $^g\mathbf T := g\mathbf T g^{-1}$ is another F-stable maximal torus, and $w \in {\mathbf W}$ is said to be the type of $^g \mathbf T$ with respect to $\mathbf T$ . Every F-stable maximal torus arises in this manner. According to [2, Cor. 1.14], the G-conjugacy class of $^g \mathbf T$ only depends on the F-conjugacy class of the image w of the element $g^{-1}F(g) \in \mathrm N_{{\mathbf G}}(\mathbf T)$ in the Weyl group ${\mathbf W}$ . Here, two elements w and $w'$ in ${\mathbf W}$ are said to be F-conjugates if there exists some element $u \in {\mathbf W}$ such that $w = u w' F(u)^{-1}$ . For every $w\in {\mathbf W}$ , we fix $\mathbf T_w$ an F-stable maximal torus of type w with respect to $\mathbf T$ . The Deligne–Lusztig induction of the trivial representation of $\mathbf T_w$ is the virtual representation of G defined by the formula

$$ \begin{align*}R_w := \sum_{i\geq 0} (-1)^i{\mathrm H}^i_c(X_{\emptyset}(w)).\end{align*} $$

According to [2, Th. 1.6], the virtual representation $R_w$ only depends on the F-conjugacy class of w in ${\mathbf W}$ . An irreducible representation of G is said to be unipotent if it occurs in $R_w$ for some $w\in {\mathbf W}$ . The set of isomorphism classes of unipotent representations of G is usually denoted $\mathcal E(G,1)$ following Lusztig’s notations.

Assume that the Coxeter graph of the reductive group ${\mathbf G}$ is a union of subgraphs of type $A_m$ (for various m). Let be the set of isomorphism classes of irreducible representations of its Weyl group ${\mathbf W}$ . The action of the Frobenius F on ${\mathbf W}$ induces an action on , and we consider the fixed point set . Then, [12, Th. 2.2] establishes the following classification.

Theorem 9. There is a bijection between and the set of isomorphism classes of irreducible unipotent representations of $G = {\mathbf G}^F$ .

We recall how the bijection is constructed. If is an irreducible F-stable representation of ${\mathbf W}$ , according to [12], there is a unique automorphism $\widetilde {F}$ of V of finite order such that

$$ \begin{align*}R(V) := \frac{1}{|{\mathbf W}|}\sum_{w\in {\mathbf W}} \mathrm{Trace}(w\circ \widetilde{F} \,|\, V)R_w\end{align*} $$

is an irreducible representation of G. Then the map $V \mapsto R(V)$ is the desired bijection.

In the case ${\mathbf G} = \mathrm {GL}_n$ with the Frobenius morphism F being either standard or twisted (i.e., $G = \mathrm {GL}_n(q)$ or $\mathrm {U}_n(q)$ ), we have an equality . Moreover, the automorphism $\widetilde {F}$ is the identity in the former case and multiplication by $w_0$ on the latter, where $w_0$ is the element of maximal length in ${\mathbf W}$ . Thus, in both cases, the irreducible unipotent representations of G are classified by the irreducible representations of the Weyl group ${\mathbf W}\simeq \mathfrak S_n$ , which in turn are classified by partitions of n or equivalently by Young diagrams. We now recall the underlying combinatorics behind the representation theory of the symmetric group. A general reference is [9].

A partition of n is a tuple $\lambda = (\lambda _1 \geq \cdots \geq \lambda _r)$ with $r\geq 1$ , and the $\lambda _i$ ’s are positive integers such that $\lambda _1 + \cdots + \lambda _r = n$ . The integer n is called the length of the partition, and it is also denoted by $|\lambda |$ . If a partition has a series of repeating integers, it is common to write it shortly with an exponent. For instance, the partition $(3,3,2,2,1)$ of $11$ will be denoted $(3^2,2^2,1)$ . Partitions of n are naturally identified with Young diagrams of size n. The diagram attached to $\lambda $ has r rows consisting successively of $\lambda _1, \ldots ,\lambda _r$ boxes.

To any partition $\lambda $ of n, one can naturally associate an irreducible representation $\chi _{\lambda }$ of the symmetric group $\mathfrak S_n$ . An explicit construction is given, for instance, by the notion of Specht modules as explained in [9, §7.1]. In particular, the character $\chi _{(n)}$ is trivial, whereas the character $\chi _{(1^n)}$ is the signature.

We recall the Murnaghan–Nakayama rule, which gives a recursive formula to evaluate the characters $\chi _{\lambda }$ . We first need to introduce skew Young diagrams. Consider a pair $\lambda $ and $\mu $ of two partitions, respectively, of integers $n+k$ and k. Assume that the Young diagram of $\mu $ is contained in the Young diagram of $\lambda $ . By removing the boxes corresponding to $\mu $ from the diagram of $\lambda $ , one finds a shape consisting of n boxes denoted by $\lambda \setminus \mu $ . Any such shape is called a skew Young diagram of size n. It is said to be connected if one can go from a given box to any other by moving in a succession of adjacent boxes.

For example, consider the partition $\lambda = (3^2,2^2,1)$ and let us define the partitions $\mu _1 = (2^2)$ , $\mu _2 = (3,1^2)$ , and $\mu _3 = (2,1)$ . The diagrams below correspond, from left to right, to the skew Young diagrams $\lambda \setminus \mu _i$ for $i=1,2,3$ .

The skew Young diagram $\lambda \setminus \mu _1$ is not connected, whereas the others are connected. A skew Young diagram is said to be a border strip if it is connected and if it does not contain any $2\times 2$ square. The height of a border strip is defined as its number of rows minus $1$ . For instance, among the three skew Young diagrams above, only $\lambda \setminus \mu _2$ is a border strip. Its size is $6$ , and its height is $3$ .

The characters $\chi _{\lambda }$ are class functions, so we only need to specify their values on conjugacy classes of the symmetric group $\mathfrak S_n$ . These conjugacy classes are also naturally labeled by partitions of n. Indeed, up to ordering any permutation, $\sigma \in \mathfrak S_n$ can be uniquely decomposed as a product of $r\geq 1$ cycles $c_1,\ldots ,c_r$ with disjoint supports. We denote by $\nu _i$ the cycle length of $c_i$ , and we order them so that $\nu _1 \geq \cdots \geq \nu _r$ . We allow cycles to have length $1$ , so that the union of the supports of all the $c_i$ ’s is $\{1,\ldots ,n\}$ . Thus, we obtain a partition $\nu = (\nu _1,\ldots ,\nu _r)$ of n, which is called the cycle type of the permutation $\sigma $ . Two permutations are conjugates in $\mathfrak S_n$ if and only if they share the same cycle type. We denote by $\chi _{\lambda }(\nu )$ the value of the character $\chi _{\lambda }$ on the conjugacy class labelled by $\nu $ .

Theorem 10. Let $\lambda $ and $\nu $ be two partitions of n. We have

$$ \begin{align*}\chi_{\lambda}(\nu) = \sum_{S} (-1)^{\mathrm{ht}(S)}\chi_{\lambda\setminus S}(\nu\setminus \nu_1),\end{align*} $$

where S runs over the set of all border strips of size $\nu _1$ in the Young diagram of $\lambda $ , such that removing S from $\lambda $ gives again a Young diagram. Here, the integer $\mathrm {ht}(S) \in \mathbb Z_{\geq 0}$ is the height of the border strip S, the Young diagram $\lambda \setminus S$ is the one obtained by removing S from $\lambda $ , and $\nu \setminus \nu _1$ is the partition of $n - \nu _1$ obtained by removing $\nu _1$ from $\nu $ .

Applying the Murnaghan–Nakayama rule in successions results in the value of $\chi _{\lambda }(\nu )$ . We see, in particular, that $\chi _{(n)}$ is the trivial character, whereas $\chi _{(1^n)}$ is the signature. We illustrate the computations with $\lambda = (3^2,2^2,1)$ and $\nu = (4^2,3)$ . There are only two eligible border strips of size $4$ in the diagram of $\lambda $ , as marked below.

Both border strips have height $2$ . Thus, the formula gives

$$ \begin{align*}\chi_{(3^2,2^2,1)}(4^2,3) = \chi_{(3^2,1)}(4,3) + \chi_{(3,1^4)}(4,3).\end{align*} $$

In each of the two Young diagrams obtained after removal of the border strips, there is only one eligible strip of size $4$ , and eventually the three last remaining boxes form the final border strip of size $3$ .

Taking the heights of the border strips into account, we find

$$ \begin{align*} \chi_{(3^2,1)}(4,3) = - \chi_{(3)}(3) = - \chi_{\emptyset} = -1, & & \chi_{(3,1^4)}(4,3) = - \chi_{(3)}(3) = - \chi_{\emptyset} = -1. \end{align*} $$

Here, $\emptyset $ denotes the empty partition. The computation finally gives $\chi _{(3^2,2^2,1)}(4^2,3) = -2$ .

The irreducible unipotent representation of ${\mathrm U}_n(q)$ (resp. $\mathrm {GL}_n(q)$ ) associated with $\chi _{\lambda }$ by the bijection of Theorem 9 is denoted by $\rho _{\lambda }^{{\mathrm U}}$ (resp. $\rho _{\lambda }^{\mathrm {GL}}$ ). The partition $(n)$ corresponds to the trivial representation and $(1^n)$ to the Steinberg representation in both cases. We will omit the superscript when the group we are talking about is clear from the context. The degrees of the representations $\rho _{\lambda }^{\mathrm {GL}}$ and $\rho _{\lambda }^{{\mathrm U}}$ are given by expressions known as hook formula. Given a box in the Young diagram of $\lambda $ , its hook length is $1$ plus the number of boxes lying below it or on its right. For instance, in the following figure, the hook length of every box of the Young diagram of $\lambda = (3^2,2^2,1)$ has been written inside it.

Proposition 11. Let $\lambda = (\lambda _1 \geq \cdots \geq \lambda _r)$ be a partition of n. The degrees of the irreducible unipotent representations $\rho _{\lambda }^{\mathrm {GL}}$ and $\rho _{\lambda }^{{\mathrm U}}$ (resp. of $\mathrm {GL}_n(q)$ and ${\mathrm U}_n(q)$ ) are given by the following formulas:

where $a(\lambda ) = \sum _{i=1}^r (i-1)\lambda _i$ .

We recall from [6, §3.1 and §3.2] some definitions on classical Harish-Chandra theory. A parabolic subgroup of G is a subgroup $P\subset G$ such that there exists an F-stable parabolic subgroup ${\mathbf P}$ of ${\mathbf G}$ with $P = {\mathbf P}^F$ . A Levi complement of G is a subgroup $L \subset G$ such that there exists an F-stable Levi complement $\mathbf L$ of ${\mathbf G}$ , contained inside some F-stable parabolic subgroup, such that $L = \mathbf L^F$ . Any parabolic subgroup P of G has a Levi complement L. Let $U = {\mathbf U}^F$ be the F-fixed points of the unipotent radical ${\mathbf U}$ of ${\mathbf P}$ . The Harish-Chandra induction and restriction functors are defined by the following formulas.

$$ \begin{align*} \mathrm{R}^G_{L\subset P}: \mathrm{Rep}(L) & \to \mathrm{Rep}(G) & {}^*\mathrm{R}^G_{L\subset P}: \mathrm{Rep}(G) & \to \mathrm{Rep}(L) \\ \sigma & \mapsto {\mathbb C}[G/U]\otimes_{{\mathbb C}[L]}\sigma & \rho & \mapsto \mathrm{Hom}_G({\mathbb C}[G/U],\rho) \end{align*} $$

Here, $\mathrm {Rep}(G)$ is the category of complex representations of G, and similarly for $\mathrm {Rep}(L)$ . These two functors are adjoint, and up to isomorphism, they do not depend on the choice of the parabolic subgroup P containing the Levi complement L. For this reason, we will denote the functors ${\mathrm R}^G_L$ and ${}^*{\mathrm R}^G_L$ instead. An irreducible representation of G is called cuspidal if its Harish-Chandra restriction to any proper Levi complement is zero. We consider pairs $(L,X)$ where L is a Levi complement of G and X is an irreducible representation of L. We define an order on the set of such pairs by setting $(L,X) \leq (M,Y)$ if $L\subset M$ and if X occurs in the Harish-Chandra restriction of Y to L. A pair is said to be cuspidal if it is minimal with respect to this order, in which case X is a cuspidal representation of L. If $(L,X)$ is a cuspidal pair, we will denote by $[L,X]$ its conjugacy class under G. Given a cuspidal pair $(L,X)$ of G, its associated Harish-Chandra series $\mathcal E(G,(L,X))$ is defined as the set of isomorphism classes of irreducible constituents in the induction of X to G. Each series is nonempty. Two of them are either disjoint or equal, the latter occurring if and only if the two cuspidal pairs are conjugates in G. Thus, the series are indexed by the conjugacy classes $[L,X]$ of cuspidal pairs. Moreover, the isomorphism class of any irreducible representation of G belongs to some Harish-Chandra series. Thus, Harish-Chandra series form a partition of the set of isomorphism classes of irreducible representations of G. If $\rho $ is an irreducible representation of G, the conjugacy class $[L,X]$ corresponding to the series to which $\rho $ belongs is called the cuspidal support of $\rho $ . If T denotes a maximal torus in G, then the series $\mathcal E(G,(T,1))$ is called the unipotent principal series of G.

For the general linear group $\mathrm {GL}_n(q)$ , there is no unipotent cuspidal representation unless $n=1$ , in which case the trivial representation is cuspidal. Moreover, the unipotent representations all belong to the principal series. The situation for the unitary group is very different. First, by [11, Prop. 9.2 and Prop. 9.4], there exists an irreducible unipotent cuspidal representation of ${\mathrm U}_n(q)$ if and only if n is an integer of the form $n = \frac {x(x+1)}{2}$ for some $x\geq 0$ , and when that is the case it is the one associated with the partition $\Delta _x := (x, x-1,\ldots ,1)$ , whose Young diagram has the distinctive shape of a reversed staircase. Here, as a convention, ${\mathrm U}_0(q)$ denotes the trivial group.

For example, here are the Young diagrams of $\Delta _1,\Delta _2$ , and $\Delta _3$ . Of course, the one of $\Delta _0$ is the empty diagram.

Furthermore, the unipotent representations decompose nontrivially into various Harish-Chandra series, as we recall from [6, §4.3]. We consider an integer $x\geq 0$ such that n decomposes as $n = 2a + \frac {x(x+1)}{2}$ for some $a\geq 0$ . We also consider the standard Levi complement $L_x \simeq \mathrm {GL}_1(q^2)^a \times {\mathrm U}_{\frac {x(x+1)}{2}}(q)$ , which corresponds to the choice of simple reflexions $s_{a+1}, \ldots , s_{n-a-1}$ . We write $\rho _x$ for the inflation of $\rho ^{{\mathrm U}}_{\Delta _x}$ to an irreducible representation of $L_x$ . Then $\mathcal E({\mathrm U}_n(q),1)$ decomposes as the disjoint union of all the Harish-Chandra series $\mathcal E({\mathrm U}_n(q), (L_x,\rho _x))$ for all possible choices of x. With these notations, the principal unipotent series corresponds to $x=0$ if n is even and to $x=1$ if n is odd. Given an irreducible unipotent representation $\rho _{\lambda }$ of ${\mathrm U}_n(q)$ , there is a combinatorial way of determining the Harish-Chandra series to which it belongs. We consider the Young diagram of $\lambda $ . We call domino any pair of adjacent boxes in the diagram. It may be either vertical or horizontal. We remove dominoes from the rim of the diagram of $\lambda $ so that the resulting shape is again a Young diagram, until one cannot proceed further. This process results in the Young diagram of the partition $\Delta _x$ for some $x\geq 0$ , and it is called the $2$ -core of $\lambda $ . It does not depend on the successive choices for the dominoes. Then, the representation $\rho _{\lambda }$ belongs to the series $\mathcal E({\mathrm U}_n(q),(L_x,\rho _x))$ if and only if $\lambda $ has $2$ -core $\Delta _x$ .

For instance, the diagram $\lambda = (3^2,2^2,1)$ has $2$ -core $\Delta _1$ , as it can be determined by the following steps. We put crosses inside the successive dominoes that we remove from the diagram. Thus, the unipotent representation $\rho _{\lambda }$ of $\mathrm {U}_{11}(q)$ belongs to the unipotent principal series $\mathcal E({\mathrm U}_{11}(q),(L_1,\rho _1))$ .

3 Computing Harish–Chandra induction of unipotent representations in the finite unitary group

We recall from [6, §3.2] how Harish-Chandra induction of unipotent representations can be explicitly computed. Let $W = {\mathbf W}^F$ be the Weyl group of G. It is still a Coxeter group, whose set of simple reflexions S is identified with the set of F-orbits on ${\mathbf S}$ . Let $(L,X)$ be a cuspidal pair of G. The relative Weyl group of L is given by $W_G(L) := N_{{\mathbf G}}(\mathbf L)^F/L\subset W$ . The relative Weyl group of the pair $(L,X)$ , also called the ramification group of X in [8], is the subgroup $W_G(L,X)$ of $W_G(L)$ consisting of elements w such that $wX \simeq X$ , where $wX$ denotes the representation $wX(g) := X(wgw^{-1})$ of L. It is yet again a Coxeter group if ${\mathbf G}$ has a connected center or if X is unipotent. Theorem 3.2.5 of [6] establishes an isomorphism between the endomorphism algebra of the induced representation ${\mathrm R}_{L}^{G}(X)$ and the complex group ring of the ramification group $W_G(L,X)$ . In particular, this gives an bijection between the Harish-Chandra series $\mathcal E(G,(L,X))$ and the set $\mathrm {Irr}(W_G(L,X))$ of isomorphism classes of irreducible complex characters of $W_G(L,X)$ . These bijections for G and for various Levi complements in G can be chosen to be compatible with Harish-Chandra induction. This is known as Howlett and Lehrer’s comparison theorem, which was proved in (see also [6, Th. 3.2.7]).

Theorem 12. Let $(L,X)$ be a cuspidal pair for the finite group of Lie type G. For every Levi complement M in G containing L, the bijection between $\mathrm {Irr}(W_M(L,X))$ and $\mathcal E(M,(L,X))$ can be taken so that the diagrams

are commutative. Here, $\mathrm {Ind}$ and $\mathrm {Res}$ on the right-hand side of the diagrams are the classical induction and restriction functors for representations of finite groups.

In other words, computing Harish-Chandra induction and restrictions of representations in G can be entirely done at the level of the associated Coxeter groups. In order to use this statement for unitary groups, we need to make the horizontal arrows explicit and to understand the combinatorics behind induction and restriction of the irreducible representations of the relevant Coxeter groups. This has been explained consistently in [5] for classical groups.

We focus on the case of the unitary group. Let $x\geq 0$ such that $n = 2a + \frac {x(x+1)}{2}$ for some $a\geq 0$ . We consider the cuspidal pair $(L_x,\rho _x)$ with $L_x = \mathrm {GL}_1(q^2)^a\times \mathrm {U}_{\frac {x(x+1)}{2}}(q)$ . The relative Weyl group $W_{\mathrm {U}_n(q)}(L_x)$ is isomorphic to the Coxeter group of type $B_a$ , which is usually denoted by $W_a$ . Indeed, the Weyl group $W_{{\mathrm U}_n(q)}(L_x)$ admits a presentation by elements $\sigma _1,\ldots , \sigma _{a-1}$ and $\theta $ of order $2$ satisfying the relations

$$ \begin{align*} \theta\sigma_1\theta\sigma_1 & = \sigma_1 \theta \sigma_1 \theta, & \theta\sigma_i & = \sigma_i \theta, & & \forall \; 2\leq i \leq m-1, \\ \sigma_i \sigma_{i+1} \sigma_i & = \sigma_{i+1} \sigma_i \sigma_{i+1}, & \sigma_i \sigma_j & = \sigma_j \sigma_i, & & \forall\; |i-j| \geq 2. \end{align*} $$

Explicitly, the element $\sigma _i$ is represented by the permutation matrix of the double transposition $(i\quad i+1)(n-i\quad n-i+1)$ and the element $\theta $ by the matrix of the transposition $(1 \quad n)$ , all of which belong to $N_{{\mathrm U}_n(q)}(L_x)$ . This presentation coincide with the Coxeter group $W_a$ of type $B_a$ (see in [7, §1.4.1]). Moreover, the ramification group $W_{{\mathrm U}_n(q)}(L_x,\rho _x)$ is equal to the whole of $W_{{\mathrm U}_n(q)}(L_x) \simeq W_a$ . The identification between the ramification group and the Coxeter group $W_a$ is naturally induced by the isomorphism between the absolute Weyl group ${\mathbf W}$ and the symmetric group $\mathfrak S_n$ . In order to proceed further, we need to explain the representation theory of the group $W_a$ . For $1\leq i \leq a-1$ , we define $\theta _i = \sigma _i\ldots \sigma _1\theta \sigma _{1}\ldots \sigma _{i}$ . In particular, $\theta _0 = \theta $ . Following [7, §3.4.2], we define signed blocks to be elements of the following form. Given $k\geq 0$ and $e\geq 1$ such that $k + e \leq a$ , the positive (resp. negative) block of length e starting at k is

$$ \begin{align*} b^+_{k,e} := \sigma_{k+1}\sigma_{k+2}\ldots \sigma_{k+e-1}, & & b^-_{k,e} := \theta_k\sigma_{k+1}\sigma_{k+2}\ldots \sigma_{k+e-1}. \end{align*} $$

A bipartition of a is an ordered pair $(\alpha ,\beta )$ where $\alpha $ is a partition of some integer $0\leq j \leq a$ and $\beta $ is a partition of $a - j$ . Given a bipartition $(\alpha ,\beta )$ of a and writing $\alpha = (\alpha _1,\ldots ,\alpha _r)$ and $\beta = (\beta _1,\ldots ,\beta _s)$ , we define the element

$$ \begin{align*}w_{\alpha,\beta} := b^-_{k_1,\beta_1}\ldots b^-_{k_s,\beta_s}b^+_{k_{s+1},\alpha_1}\ldots b^+_{k_{s+r},\alpha_r},\end{align*} $$

where $k_1 = 0$ , $k_{i+1} = k_i + \beta _i$ if $1\leq i \leq s$ , and $k_{i+1} = k_i + \alpha _{i - s}$ if $s+1\leq i \leq s+r - 1$ . In particular, we have $k_{r+s} + \alpha _r = a$ . According to [7, Prop. 3.4.7], the conjugacy classes in $W_a$ are labeled by bipartitions of a, and a representative of minimal length of the conjugacy class corresponding to the bipartition $(\alpha ,\beta )$ is given by $w_{\alpha ,\beta }$ . Thus, the irreducible representations of $W_a$ can be labeled by bipartitions of a as well. An explicit construction of these irreducible representations is given in [7, §5.5]. We will not recall it; however, we may again give a method to compute the character values, similar to the Murnaghan–Nakayama formula. The character of the irreducible representation of $W_a$ associated in [7] with the bipartition $(\alpha ,\beta )$ of a will be denoted $\chi _{\alpha ,\beta }$ . If $(\gamma ,\delta )$ is another bipartition of a, we denote by $\chi _{\alpha ,\beta }(\gamma ,\delta )$ the value of the character $\chi _{\alpha ,\beta }$ on the conjugacy class of $W_a$ labeled by $(\gamma ,\delta )$ .

One can think of a bipartition $(\alpha ,\beta )$ of a as an ordered pair of two Young diagrams of combined size a. A border strip of a bipartition $(\alpha ,\beta )$ is a border strip either of the partition $\alpha $ or of $\beta $ . The height of a border strip is defined in the same way.

Theorem 13. Let $(\alpha ,\beta )$ and $(\gamma ,\delta )$ be two bipartitions of a. If $\gamma \not = \emptyset $ , let $\epsilon = 1$ and let x be the last integer in the partition $\gamma $ . If $\gamma = \emptyset $ , let $\epsilon = -1$ and let x be the last integer of the partition $\delta $ . We have

$$ \begin{align*}\chi_{\alpha,\beta}(\gamma,\delta) = \sum_S (-1)^{\mathrm{ht}(S)}\epsilon^{f_S}\chi_{(\alpha,\beta)\setminus S}((\gamma,\delta)\setminus x),\end{align*} $$

where S runs over the set of all border strips of size x in the bipartition $(\alpha ,\beta )$ , such that removing S from $(\alpha ,\beta )$ gives again a pair of Young diagrams. Here, the pair of Young diagrams $(\alpha ,\beta )\setminus S$ is the one obtained after removing S, and $(\gamma ,\delta )\setminus x$ is the bipartition obtained by removing x from $(\gamma ,\delta )$ . Eventually, the integer $f_S$ is $0$ if S is a border strip of $\alpha $ , and it is $1$ if S is a border strip of $\beta $ .

Applying this formula in successions results in the value of $\chi _{(\alpha ,\beta )}(\gamma ,\delta )$ . In particular, one sees that $\chi _{(a),\emptyset }$ is the trivial character and that $\chi _{\emptyset ,(1^a)}$ is the signature character of $W_a$ . We illustrate the computations with $(\alpha ,\beta ) = ((3,1^2),(4,2))$ and $(\gamma ,d) = ((4),(5,2))$ . There is only eligible border strip of size $4$ in the pair of diagrams $(\alpha ,\beta )$ , as marked below.

This border strip S has height $1$ . It was taken in the diagram of $\beta $ , so $f_S = 1$ . Since $\gamma \not = \emptyset $ , we have $\epsilon = 1$ . Applying the formula, we obtain

$$ \begin{align*}\chi_{(3,1^2),(4,2)}((4),(5,2)) = - \chi_{(3,1^2),(1^2)}(\emptyset,(5,2)).\end{align*} $$

We are now looking for border strips of size $2$ in the pair of diagrams of the bipartition $(3,1^2),(1^2)$ . Three of them are eligible, as marked below.

These three border strips have respective heights $1,0$ , and $1$ . The corresponding values of $f_S$ are, respectively, $1$ , $0$ , and $0$ . Moreover, the partition $\gamma $ is now empty, so $\epsilon = -1$ . The formula gives

$$ \begin{align*}\chi_{(3,1^2),(1^2)}(\emptyset,(5,2)) = \chi_{(3,1^2),\emptyset}(\emptyset,(5)) + \chi_{(1^3),(1^2)}(\emptyset,(5)) - \chi_{(3),(1^2)}(\emptyset,(5)).\end{align*} $$

In the bipartitions $((1^3),(1^2))$ and $((3),(1^2))$ , there is no border strip of size $5$ at all. Thus, the formula tells us that the corresponding character values are $0$ . On the other hand, the bipartition $((3,1^2),\emptyset )$ consists of a single border strip of size $5$ and height $2$ . The formula gives

$$ \begin{align*}\chi_{(3,1^2),\emptyset}(\emptyset,(5)) = \chi_{\emptyset} = 1.\end{align*} $$

Putting things together, we deduce that $\chi _{(3,1^2),(4,2)}((4),(5,2)) = -1$ .

We may now describe the horizontal arrows in Theorem 12 for the unitary group. To do this, we need an alternate labeling of the irreducible unipotent representations of the unitary group. We refer to [5] for the details. The new labeling of the irreducible unipotent representations of ${\mathrm U}_n(q)$ involves triples of the form $(\Delta _x,\alpha ,\beta )$ where x is a nonnegative integer such that $n = 2a + \frac {x(x+1)}{2}$ for some integer $a\geq 0$ , and where $(\alpha ,\beta )$ is a bipartition of a. The corresponding representation will be denoted $\rho _{\Delta _x,\alpha ,\beta }$ . With this labeling, the unipotent Harish-Chandra series $\mathcal E({\mathrm U}_n(q),(L_x,\rho _x))$ consists precisely of all the representations $\rho _{\Delta _x,\alpha ,\beta }$ with $(\alpha ,\beta )$ varying over all bipartitions of a. The bijection $\mathbb Z\mathcal E({\mathrm U}_n(q),(L_x,\rho _x)) \xrightarrow {\sim } \mathbb Z\mathrm {Irr}(W_{{\mathrm U}_n(q)}(L_x,\rho _x))$ involved in the Comparison theorem simply sends $\rho _{\Delta _x,\alpha ,\beta }$ to $\chi _{\alpha ,\beta }$ . Here, we made use of the identification $W_{{\mathrm U}_n(q)}(L_x,\rho _x) \simeq W_a$ .

More generally, if M is a standard Levi complement in ${\mathrm U}_n(q)$ containing $L_x$ , we may write $M \simeq {\mathrm U}_b(q)\times \mathrm {GL}_{a_1}(q^2) \times \cdots \times \mathrm {GL}_{a_r}(q^2)$ where $n = 2(a_1 + \cdots + a_r) + b$ and $b\geq \frac {x(x+1)}{2}$ . The irreducible unipotent representations of M in the Harish-Chandra series $\mathcal E(M,(L_x,\rho _x))$ are those of the form $\rho _{\Delta _x,\alpha ,\beta }\boxtimes \rho ^{\mathrm {GL}}_{\lambda _1}\boxtimes \cdots \boxtimes \rho ^{\mathrm {GL}}_{\lambda _r}$ where $\lambda _i$ is a partition of $a_i$ for $1\leq i \leq r$ and $(\alpha ,\beta )$ is a bipartition of the integer $c:= \frac {1}{2}\left (b - \frac {x(x+1)}{2}\right )$ . On the other hand, the relative Weyl group $W_M(L_x,\rho _x)$ can be identified with the subgroup of $W_{{\mathrm U}_n(q)}(L_x,\rho _x) \simeq W_a$ isomorphic to the product $W_c\times \mathfrak S_{a_1}\times \cdots \times \mathfrak S_{a_r}$ . (Note that $c + a_1 + \cdots + a_r = a$ .) Concretely, the $W_c$ -component is generated by the elements $\theta ,\sigma _1,\ldots , \sigma _{c-1}$ , the $\mathfrak S_{a_1}$ -component by the elements $\sigma _{c+1},\ldots ,\sigma _{c+a_1-1}$ , and so on. Irreducible characters of $W_M(L_x,\rho _x)$ have the shape $\chi _{\alpha ,\beta }\boxtimes \chi _{\lambda _1} \boxtimes \cdots \boxtimes \chi _{\lambda _r}$ where $(\alpha ,\beta )$ is a bipartition of c and $\lambda _i$ is a partition of $a_i$ for $1\leq i \leq r$ . Then, according to [5, §4], the bijection $\mathbb Z\mathcal E(\mathrm M,(L_x,\rho _x)) \xrightarrow {\sim } \mathbb Z\mathrm {Irr}(W_M(L_x,\rho _x))$ involved in Theorem 12 sends $\rho _{\Delta _x,\alpha ,\beta }\boxtimes \rho ^{\mathrm {GL}}_{\lambda _1}\boxtimes \cdots \boxtimes \rho ^{\mathrm {GL}}_{\lambda _r}$ to $\chi _{\alpha ,\beta }\boxtimes \chi _{\lambda _1} \boxtimes \cdots \boxtimes \chi _{\lambda _r}$ .

We explain how the two different labelings of the irreducible unipotent representations of $\mathrm {U}_n(q)$ are related. To do this, one needs the notion of $2$ -quotient. For the following definitions, we allow partitions to have $0$ terms at the end. Thus, let us write $\lambda = (\lambda _1 \geq \cdots \geq \lambda _r)$ with $\lambda _r \geq 0$ . The $\beta $ -set of $\lambda $ is the sequence of decreasing nonnegative integers $\beta _i := \lambda _i + r - i$ for $1\leq i \leq r$ . Mapping a partition $\lambda $ to its $\beta $ -set gives a bijection between the set of partitions having r terms and the set of decreasing sequences of nonnegative integers of length r. The inverse mapping sends a sequence $(\beta _1> \cdots > \beta _r \geq 0)$ to the partition $\lambda $ given by $\lambda _i = \beta _i + i - r$ . Let $\lambda $ be a partition of n as above, and let $\beta $ be its $\beta $ -set. We let $\beta _{\text {even}}$ (resp. $\beta _{\text {odd}}$ ) be the subsequence consisting of all even (resp. odd) integers of $\beta $ . Then, we define the following sequences:

$$ \begin{align*} \beta^0 := \left(\frac{\beta_i}{2} \,\middle|\, \beta_i \in \beta_{\text{even}}\right), & & \beta^1 := \left(\frac{\beta_i - 1}{2} \,\middle|\, \beta_i \in \beta_{\text{odd}}\right). \end{align*} $$

The sequences $\beta ^0$ and $\beta ^1$ are the $\beta $ -sets of two partitions, which we call $\mu ^0$ and $\mu ^1$ , respectively. Then, the $2$ -quotient of $\lambda $ is the bipartition $(\mu ^0,\mu ^1)$ if r is odd, and $(\mu ^1,\mu ^0)$ if r is even. We note that the ordering of $\mu ^0$ and $\mu ^1$ in the $2$ -quotient may vary in the literature. Here, we followed the conventions of §1 of [5]. A different ordering is used in [9, §2.7]. In [9, Th. 2.7.37], another construction of the $2$ -quotient using Young diagrams is proposed. Let $\lambda '$ be another partition which differs from $\lambda $ only by $0$ terms at the end. While the $\beta $ -sets of $\lambda $ and $\lambda '$ are not necessarily the same, the resulting $2$ -quotients are equal up to $0$ terms at the end of the partitions. Thus, from now on, we identify all partitions differing only from $0$ terms by removing all of them. The $2$ -quotient of a partition is then well defined. By [9, Th. 2.7.30], we have the following result.

Theorem 14. A partition $\lambda $ is uniquely characterized by the data of its $2$ -core $\Delta _x$ and its $2$ -quotient $(\lambda ^0,\lambda ^1)$ . Moreover, the lengths of these partitions are related by the equation

$$ \begin{align*} |\lambda| = |\Delta_x| +2(|\lambda^0| + |\lambda^1|) \end{align*} $$

and $|\Delta _x| = \frac {x(x+1)}{2}$ .

For instance, the $2$ -quotient of the partition $\lambda = (3^2,2^2,1)$ is $(2^2,1)$ . Recall that the $2$ -core of $\lambda $ is $\Delta _1$ . Thus, the equation on the lengths of the partitions is satisfied, as we have $11 = 1 + 2(4+1)$ .

We may now relate the two labelings $\{\rho ^{{\mathrm U}}_{\lambda }\}$ and $\{\rho _{\Delta _x,\alpha ,\beta }\}$ of the irreducible unipotent representations of ${\mathrm U}_n(q)$ together (see [5, Appendix]).

Proposition 15. Let $\lambda $ be a partition of n. Denote by $\Delta _{y}$ its $2$ -core and by $(\lambda ^0,\lambda ^1)$ its $2$ -quotient. On the other hand, let $x\geq 0$ be such that $n = 2a + \frac {x(x+1)}{2}$ for some $a\geq 0$ and let $(\alpha ,\beta )$ be a bipartition of a. Then the irreducible representations $\rho ^{U}_{\lambda }$ and $\rho _{\Delta _{x},\alpha ,\beta }$ are equivalent if and only if $x=y$ and $(\lambda ^0,\lambda ^1) = (\alpha ,\beta )$ if x is even or $(\lambda ^0,\lambda ^1) = (\beta ,\alpha )$ if x is odd.

For instance, for $\lambda = (3^2,2^2,1)$ , the representation $\rho _{\lambda }^{\mathrm {U}}$ is equivalent to $\rho _{\Delta _1,(1),(2^2)}$ .

In order to apply the comparison theorem for unitary groups, it remains to understand how to compute inductions in Coxeter groups of type B. Such computations are carried out in §6.1 of [7]. It turns out that we will only need one specific case of such inductions, and the corresponding method is known as the Pieri rule for groups of type B (see [7, §6.1.9]).

Proposition 16. Let $a \geq 1$ and consider $r,s \geq 0$ such that $r+s = a$ . We think of the group $W_r \times \mathfrak S_s$ as a subgroup of $W_a$ .

• – Let $(\alpha ,\beta )$ be a bipartition of r. Then the induced character

  $$ \begin{align*}\mathrm{Ind}_{W_r \times \mathfrak S_s}^{W_a}\left(\chi_{(\alpha,\beta)} \boxtimes \chi_{(s)} \right)\end{align*} $$

  is the multiplicity-free sum of all the characters $\chi _{\gamma ,\delta }$ such that for some $0\leq k \leq s$ , the Young diagram of $\gamma $ (resp. $\delta $ ) can be obtained from that of $\alpha $ (resp. $\beta $ ) by adding k boxes (resp. $s-k$ boxes) so that no two of them lie in the same column.

• – Let $(\gamma ,\delta )$ be a bipartition of a. The restricted character

  $$ \begin{align*}\mathrm{Res}_{W_r}^{W_a}\left(\chi_{\gamma,\delta}\right)\end{align*} $$

  is the multiplicity-free sum of all the characters $\chi _{(\alpha ,\beta )}$ such that for some $0\leq k \leq s$ , the Young diagram of $\alpha $ (resp. $\beta $ ) can be obtained from that of $\gamma $ (resp. $\delta $ ) by deleting k boxes (resp. $s-k$ boxes) so that no two of them lie in the same column.

We will use this rule on concrete examples in the sections that follow.

4 The cohomology of the Coxeter variety for the unitary group

In this section, we describe the cohomology of the Coxeter varieties for the unitary groups in odd dimension in terms of the classification of unipotent representations that we recalled in the previous sections. The cohomology groups are entirely understood by the work of Lusztig in [10]. Let $t\geq 0$ . The Coxeter variety for ${\mathrm U}_{2t+1}(q)$ is the Deligne–Lusztig variety $X_{\emptyset }(\mathrm {cox})$ , where $\mathrm {cox}$ is any Coxeter element of the Weyl group ${\mathbf W} \simeq \mathfrak S_{2t+1}$ . Recall that a Coxeter element is a permutation which can be written as the product, in any order, of exactly one simple reflexion for each F-orbit on ${\mathbf S}$ . The variety $X_{\emptyset }(\mathrm {cox})$ does not depend on the choice of the Coxeter element. It is defined over ${\mathbb F}_{q^2}$ and is equipped with commuting actions of both ${\mathrm U}_{2t+1}(q)$ and $F^2$ .

Notation. We write $X^t = X_{\emptyset }(\mathrm {cox})$ for the Coxeter variety attached to the unitary group ${\mathrm U}_{2t+1}(q)$ . We also write $\mathrm {H}_c^{\bullet }(X^t)$ instead of $\mathrm {H}_c^{\bullet }(X_{\emptyset }(\mathrm {cox})\otimes {\mathbb F},\overline {{\mathbb Q}_{\ell }})$ , where $\ell \not = p$ .

We first recall known facts on the cohomology of $X^t$ from Lusztig’s work.

Theorem 17. The following statements hold.

1. (1) The variety $X^t$ has dimension t and is affine. The cohomology group $\mathrm {H}^{t+i}_c(X^t)$ is zero unless $0\leq i \leq t$ .

2. (2) The Frobenius $F^2$ acts in a semisimple manner on the cohomology of $X^t$ .

3. (3) The group $\mathrm {H}^{2t}_c(X^t)$ is one-dimensional, the unitary group ${\mathrm U}_{2t+1}(q)$ acts trivially on it and $F^2$ has a single eigenvalue $q^{2t}$ .

4. (4) The group ${\mathrm H}^{t+i}_c(X^t)$ for $0 \leq i < t$ is the direct sum of two eigenspaces of $F^2$ , for the eigenvalues $q^{2i}$ and $-q^{2i+1}$ . Each eigenspace is an irreducible unipotent representation of $\mathrm {U}_{2t+1}(q)$ .

5. (5) If $0 \leq a \leq 2t$ , the dimension of the eigenspace of $(-q)^a$ inside the sum $\sum _{i\geq 0} {\mathrm H}_c^{t+i}(X^t)$ is given by the formula

   $$ \begin{align*}q^{\frac{(2t-a)(2t+1-a)}{2}}\prod_{j = 1}^{2t-a} \frac{q^{a + j} - (-1)^{a+j}}{q^{j} - (-1)^{j}}.\end{align*} $$

6. (6) The sum $\sum _{i\geq 0} {\mathrm H}_c^{t+i}(X^t)$ is multiplicity-free as a representation of ${\mathrm U}_{2t+1}(q)$ .

We wish to identify these unipotent representations of ${\mathrm U}_{2t+1}(q)$ occurring in the cohomology of $X^t$ . To this purpose, we start by defining the following partitions. If $0\leq a \leq 2t$ , we put $\lambda _a^t := (1 + a, 1^{2t - a})$ . Note that $\lambda _0^t = (1^{2t+1})$ and $\lambda _{2t}^t = (2t+1)$ .

Lemma 18. For $0 \leq i \leq t$ , the $2$ -core of $\lambda _{2i}^t$ is $\Delta _1$ and its $2$ -quotient is $((1^{t-i}),(i))$ . For $0 \leq i < t$ , the $2$ -core of $\lambda _{2i+1}^t$ is $\Delta _2$ and its $2$ -quotient is $((i),(1^{t-i-1}))$ .

In particular, according to Proposition 15, the irreducible unipotent representation $\rho _{\lambda _{2i}^t}$ of ${\mathrm U}_{2t+1}(q)$ is equivalent to the representation $\rho _{\Delta _1,(i),(1^{t-i})}$ , and $\rho _{\lambda _{2i+1}^t}$ to $\rho _{\Delta _2,(i),(1^{t-i-1})}$ .

Proof. The Young diagram of the partition $\lambda _a^t$ has the following shape.

The first row has an odd number of boxes when a is even, and an even number of boxes when a is odd. To compute the $2$ -core, one removes horizontal dominoes from the first row, right to left, and vertical dominoes from the first column, bottom to top. The process results in $\Delta _1$ when a is even and $\Delta _2$ when a is odd.

The partition $\lambda _a^t$ has $2t + 1 - a$ nonzero terms. Its $\beta $ -set is given by the sequence

$$ \begin{align*} \beta = (2t+1,2t-a,2t-a-1,\ldots ,1). \end{align*} $$

Assume that $a = 2i$ is even. Then the sequences $\beta ^0$ and $\beta ^1$ are given by

$$ \begin{align*} \beta^0 = (t-i,t-i-1,\ldots 1), & & \beta^1 = (t,t-i-1,t-i-2,\ldots ,0). \end{align*} $$

The sequence $\beta ^0$ has length $t-i$ , whereas $\beta ^1$ has length $t-i+1$ . The associated permutations are then, respectively, $\mu _0 = (1^{t-i})$ and $\mu _1 = (i)$ . Since $2t + 1 - a$ is odd, the $2$ -quotient is given by $(\mu _0,\mu _1)$ as claimed.

Assume now that $a = 2i+1$ is odd. Then the sequences $\beta ^0$ and $\beta ^1$ are given by

$$ \begin{align*} \beta^0 = (t-i-1,t-i-2,\ldots 1), & & \beta^1 = (t,t-i-1,t-i-2,\ldots ,0). \end{align*} $$

The sequence $\beta ^0$ has length $t-i-1$ , whereas $\beta ^1$ has length $t-i+1$ . The associated permutations are then, respectively, $\mu _0 = (1^{t-i-1})$ and $\mu _1 = (i)$ . Since $2t + 1 - a$ is even, the $2$ -quotient is given by $(\mu _1,\mu _0)$ as claimed.

We may now identify the irreducible unipotent representations occurring in the cohomology of the Coxeter variety $X^t$ .

Proposition 19. For $0 \leq i < t$ , the cohomology group of the Coxeter variety for the finite unitary group ${\mathrm U}_{2t+1}(q)$ is given by

$$ \begin{align*}{\mathrm H}_c^{t+i}(X^t) = \rho_{\lambda_{2i}^t} \oplus \rho_{\lambda_{2i+1}^t}\end{align*} $$

with the first summand corresponding to the eigenvalue $q^{2i}$ of $F^2$ and the second to $-q^{2i+1}$ . Moreover, ${\mathrm H}_c^{2t}(X^t) = \rho _{\lambda _{2t}^t}$ with eigenvalue $q^{2t}$ .

Before going to the proof, one may notice that the statement is consistent with the dimensions. Indeed, the formula given in Theorem 17(5) coincides with the hook formula for the degrees of the representations $\rho ^{{\mathrm U}}_{\lambda ^{t}_a}$ given in Proposition 11.

Proof. First, the statement on the highest cohomology group ${\mathrm H}_c^{2t}(X^t)$ follows from Theorem 17(3). It is the only cohomology group in the case $t=0$ . We will prove the formula by induction on t. Let us now assume that $t\geq 1$ and that the proposition is known for $t-1$ . If $0\leq i \leq t-1$ , we know that ${\mathrm H}_c^{t+i}(X^t)$ is the sum of two irreducible unipotent representations. So let us write

$$ \begin{align*} {\mathrm H}_c^{t+i}(X^t) = \rho_{\mu_i} \oplus \rho_{\nu_i}, \end{align*} $$

where $\mu _i$ and $\nu _i$ are two partitions of $2t+1$ , so that $\rho _{\mu _i}$ corresponds to the eigenvalue $q^{2i}$ of $F^2$ , whereas $\rho _{\nu _i}$ corresponds to $-q^{2i+1}$ .

We consider the standard Levi complement $L \simeq \mathrm {GL}_1(q^2) \times {\mathrm U}_{2t-1}(q) \subset {\mathrm U}_{2t+1}(q)$ . Let V denote the unipotent radical of the standard parabolic subgroup containing L. According to [10, Cor. 2.10], one can build a geometric isomorphism between the quotient variety $X^t/V$ and the product of the Coxeter variety for L and of a copy of $\mathbb G_m$ . Even though this geometric isomorphism is not L-equivariant, Lusztig proves that the induced map on cohomology is L-equivariant. The Coxeter variety for L is isomorphic to the Coxeter variety $X^{t-1}$ for ${\mathrm U}_{2t-1}(q)$ . We write ${}^*{\mathrm R}_{t-1}^{t}$ for the composition of the Harish-Chandra restriction from ${\mathrm U}_{2t+1}(q)$ to L, with the usual restriction from L to the subgroup ${\mathrm U}_{2t-1}(q)$ . For any nonnegative integer i, the $\mathrm {U}_{2t-1}(q), F^2$ -equivariant induced map on the cohomology is an isomorphism

(**) $$ \begin{align} {}^*{\mathrm R}_{t-1}^{t} \left({\mathrm H}^{t+i}_c(X^t)\right) \simeq {\mathrm H}^{t-1+i}_c(X^{t-1}) \oplus {\mathrm H}^{t-1+(i-1)}_c(X^{t-1})(1). \end{align} $$

Here, $(1)$ denotes the Tate twist. (The action of $F^2$ on a twist $M(n)$ is obtained from the action on the space M by multiplication with $q^{2n}$ .) The right-hand side of this identity is given by the induction hypothesis. Let us look at the left-hand side.

We fix $0\leq i \leq t-1$ , and we denote by $(\Delta _x,\alpha ,\beta )$ and by $(\Delta _y,\gamma ,\delta )$ the alternative labeling of the representations $\rho _{\mu _i}$ and $\rho _{\nu _i}$ , respectively, as in Proposition 15. By the Comparison Theorem 12 and by the Pieri rule of Proposition 16, we know that the restriction ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _x,\alpha ,\beta }\right )$ is the multiplicity-free sum of all the representations $\rho _{\Delta _x,\alpha ',\beta '}$ where the bipartition $(\alpha ',\beta ')$ can be obtained from $(\alpha ,\beta )$ by removing exactly one box, of either $\alpha $ or $\beta $ . The similar description also holds for ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _y,\gamma ,\delta }\right )$ .

By using Lemma 18 and the induction hypothesis, we may write down the identity (**) explicitly. Moreover, as it is $F^2$ -equivariant, we can identify the components corresponding to the same eigenvalues on both sides. We distinguish four different cases depending on the values of t and i.

• – Case $\mathbf {t=1}$ . We only need to consider $i=0$ . On the right-hand side of (**), the second term is $0$ because $t-1 + (i-1) = -1 < 0$ . On the other hand, the first term is $\rho _{\lambda ^0_0} \simeq \rho _{\Delta _1,\emptyset , \emptyset }$ and it corresponds to the eigenvalue $(-q)^0 = 1$ . By identifying the eigenspaces, we have ${}^*{\mathrm R}_{0}^{1} \left (\rho _{\Delta _x,\alpha ,\beta }\right ) \simeq \rho _{\Delta _1,\emptyset ,\emptyset }$ and ${}^*{\mathrm R}_{0}^{1} \left (\rho _{\Delta _y,\gamma ,\delta }\right ) = 0$ . The second equation implies that there is no box to remove from $\gamma $ nor from $\delta $ . Thus, $\gamma = \delta = \emptyset $ . The value of y is given by the relation $2t+1 = 3 = 2(0+0) + \frac {y(y+1)}{2}$ , that is, $y=2$ . This corresponds to the partition $\nu _0 = \lambda ^{1}_1$ . We notice in passing that the representation $\rho _{\nu _0}$ is the unique unipotent cuspidal representation of ${\mathrm U}_3(q)$ .

  As for $\mu _0$ , the equation ${}^*{\mathrm R}_{0}^{1} \left (\rho _{\Delta _x,\alpha ,\beta }\right ) \simeq \rho _{\Delta _1,\emptyset ,\emptyset }$ tells us that there is only one removable box from $(\alpha ,\beta )$ . After removal of this box, both partitions are empty. Thus, we deduce that $x=1$ and $(\alpha ,\beta ) = (1,\emptyset ) \text { or } (\emptyset ,1)$ . This corresponds, respectively, to $\mu _0 = \lambda ^1_2$ or $\mu _0 = \lambda ^1_0$ . That is, $\rho _{\mu _0}$ is either the trivial or the Steinberg representation of ${\mathrm U}_3(q)$ . We can deduce which one it is by comparing the degree of the representations with the formula of Theorem 17(5). According to this formula, the dimension of the eigenspace for $(-q)^0$ is $q^3$ . This is precisely the degree of the Steinberg representation $\rho _{\lambda ^{1}_0}$ as given by the hook formula in Proposition 11, and it excludes the possibility of $\rho _{\mu _0}$ being trivial. Thus, we have $\mu _0 = \lambda ^1_0$ as claimed.

From now, we assume $t\geq 2$ .

• – Case $\mathbf {i=0}$ . On the right-hand side of (**), the second term is $0$ because $t-1 + (i-1) = t-2 < t-1$ . The first term is $\rho _{\lambda ^{t-1}_0} \oplus \rho _{\lambda ^{t-1}_1} \simeq \rho _{\Delta _1,\emptyset ,(1^{t-1})} \oplus \rho _{\Delta _2,\emptyset ,(1^{t-2})}$ . Identifying the eigenspaces, we have ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _x,\alpha ,\beta }\right ) \simeq \rho _{\Delta _1,\emptyset ,(1^{t-1})}$ and ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _y,\gamma ,\delta }\right ) \simeq \rho _{\Delta _2,\emptyset ,(1^{t-2})}$ . We deduce that $x=1$ and $y=2$ . Moreover, it also follows that there is only one removable box in $(\alpha ,\beta )$ and in $(\gamma ,\delta )$ . After removal, we should obtain, respectively, $(\emptyset ,(1^{t-1}))$ and $(\emptyset ,(1^{t-2}))$ . The only possibility is that $(\alpha ,\beta ) = (\emptyset ,(1^t))$ and $(\gamma ,\delta ) = (\emptyset ,(1^{t-1}))$ . This corresponds to $\mu _0 = \lambda ^{t}_0$ and $\nu _0 = \lambda ^{t}_1$ as claimed.

• – Case $\mathbf {i=t-1}$ . On the right-hand side of (**), the first term is $\rho _{\lambda ^{t-1}_{2(t-1)}}\simeq \rho _{\Delta _1,(t-1),\emptyset }$ and the second term is $\rho _{\lambda ^{t-1}_{2(t-2)}} \oplus \rho _{\lambda ^{t-1}_{2(t-2)+1}} \simeq \rho _{\Delta _1,(t-2),(1)} \oplus \rho _{\Delta _2,(t-2),\emptyset }$ . Identifying the eigenspaces while taking the Tate twist into account, we have ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _x,\alpha ,\beta }\right ) \simeq \rho _{\Delta _1,(t-1),\emptyset } \oplus \rho _{\Delta _1,(t-2),(1)}$ and ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _y,\gamma ,\delta }\right ) \simeq \rho _{\Delta _2,(t-2),\emptyset }$ . We deduce that $x=1$ and $y=2$ . Moreover, there are two removable boxes in $(\alpha ,\beta )$ and only one removable box in $(\gamma ,\delta )$ . After removal of one of the two boxes in $(\alpha ,\beta )$ , we can get either $((t-1),\emptyset )$ or $((t-2),(1))$ , and after removal of the box in $(\gamma ,\delta )$ , we obtain $((t-2),\emptyset )$ . The only possibility is that $(\alpha ,\beta ) = ((t-1),(1))$ and $(\gamma ,\delta ) = ((t-1),\emptyset )$ . This corresponds to $\mu _{t-1} = \lambda ^t_{2(t-1)}$ and $\nu _{t-1} = \lambda ^{t}_{2(t-1)+1}$ as claimed.

• – Case $\mathbf {1\leq i \leq t-2}$ . On the right-hand side of (**), the first term is $\rho _{\lambda ^{t-1}_{2i}} \oplus \rho _{\lambda ^{t-1}_{2i+1}} \simeq \rho _{\Delta _1,(i),(1^{t-1-i})} \oplus \rho _{\Delta _2,(i),(1^{t-2-i})}$ . The second term is $\rho _{\lambda ^{t-1}_{2(i-1)}} \oplus \rho _{\lambda ^{t-1}_{2(i-1)+1}} \simeq \rho _{\Delta _1,(i-1),(1^{t-i})} \oplus \rho _{\Delta _2,(i-1),(1^{t-1-i})}$ . Identifying the eigenspaces while taking the Tate twist into account, we have ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _x,\alpha ,\beta }\right ) \simeq \rho _{\Delta _1,(i),(1^{t-1-i})} \oplus \rho _{\Delta _1,(i-1),(1^{t-i})}$ and ${}^*{\mathrm R}_{t-1}^{t} \left (\rho _{\Delta _y,\gamma ,\delta }\right ) \simeq \rho _{\Delta _2,(i),(1^{t-2-i})} \oplus \rho _{\Delta _2,(i-1),(1^{t-1-i})}$ . We deduce that $x = 1$ and $y = 2$ . Moreover, there are exactly two removable boxes from $(\alpha ,\beta )$ and from $(\gamma ,\delta )$ . After removal of one of the two boxes in $(\alpha ,\beta )$ , we can get either $((i),(1^{t-1-i}))$ or $((i-1),(1^{t-i}))$ , and after removal of one of the two boxes in $(\gamma ,\delta )$ , we can get either $((i),(1^{t-2-i}))$ or $((i-1),(1^{t-1-i}))$ . The only possibility is that $(\alpha ,\beta ) = ((i),(1^{t-i}))$ and $(\gamma ,\delta ) = ((i),(1^{t-1-i}))$ . This corresponds to $\mu _i = \lambda ^t_{2i}$ and $\nu _i = \lambda ^t_{2i+1}$ as claimed.

5 The cohomology of the variety $X_I(\mathrm {id})$

We go on with the computation of the cohomology of the variety $X_I(\mathrm {id})$ . We use the same notations as in Section 1. We first compute the cohomology of each Ekedahl–Oort stratum $X_{I_t}(w_t)$ , before using the spectral sequence associated with the stratification to conclude. Recall that $X_I(\mathrm {id})$ has dimension d, is defined over ${\mathbb F}_{q^2}$ , and is equipped with an action of $J \simeq \mathrm {U}_{2d+1}(q)$ . As before, we will write $\mathrm {H}_c^{\bullet }(X_I(\mathrm {id}))$ as a shortcut for $\mathrm {H}_c^{\bullet }(X_I(\mathrm {id})\otimes {\mathbb F},\overline {{\mathbb Q}_{\ell }})$ .

Theorem 20. The following statements hold.

1. (1) The cohomology group ${\mathrm H}_c^i(X_I(\mathrm {id}))$ is zero unless $0 \leq i \leq 2d$ . There is an isomorphism ${\mathrm H}_c^i(X_I(\mathrm {id})) \simeq {\mathrm H}_c^{2d-i}(X_I(\mathrm {id}))^{\vee }(d)$ , which is equivariant for the actions of $F^2$ and of ${\mathrm U}_{2d+1}(q)$ .

2. (2) The Frobenius $F^2$ acts like multiplication by $(-q)^i$ on ${\mathrm H}_c^i(X_I(\mathrm {id}))$ .

3. (3) For $0\leq i \leq d$ , we have

   $$ \begin{align*}{\mathrm H}_c^{2i}(X_I(\mathrm{id})) = \bigoplus_{s=0}^{\min(i,d - i)} \rho_{(2d + 1 - 2s, 2s)}.\end{align*} $$

   For $0\leq i \leq d - 1$ , we have

   $$ \begin{align*}{\mathrm H}_c^{2i+1}(X_I(\mathrm{id})) = \bigoplus_{s=0}^{\min(i,d - 1 - i)} \rho_{(2d - 2s, 2s + 1)}.\end{align*} $$

Thus, in the cohomology of $X_I(\mathrm {id})$ , all the representations associated with a Young diagram with at most two rows occur, and there is no other. Such a diagram has the following general shape.

We may rephrase the result by using the alternative labeling of the irreducible unipotent representations as in Proposition 15. The partition $(2d+1-2s,2s)$ has $2$ -core $\Delta _1$ and $2$ -quotient $(\emptyset ,(d-s,s))$ , whereas the partition $(2d-2s,2s+1)$ has $2$ -core $\Delta _2$ and $2$ -quotient $((d-1-s,s),\emptyset )$ . Thus, we have

$$ \begin{align*} \rho_{(2d + 1 - 2s, 2s)} \simeq \rho_{\Delta_1,(d-s,s),\emptyset}, & & \rho_{(2d - 2s, 2s + 1)} \simeq \rho_{\Delta_2,(d-1-s,s),\emptyset}. \end{align*} $$

In particular, all irreducible representations in the cohomology groups of even index belong to the unipotent principal series $\mathcal E({\mathrm U}_{2d +1}(q),(L_1,\rho _1))$ , whereas all the ones in the groups of odd index belong to the Harish-Chandra series $\mathcal E({\mathrm U}_{2d+1}(q),(L_2,\rho _2))$ .

Proof. Point (1) of the statement follows from a general property of the cohomology groups, namely Poincaré duality. It is due to the fact that $X_I(\mathrm {id})$ is projective and smooth. It also implies the purity of the Frobenius $F^2$ on the cohomology: we know at this stage that all eigenvalues of $F^2$ on ${\mathrm H}_c^i(X_I(\mathrm {id}))$ have complex modulus $q^i$ under any choice of an isomorphism $\overline {{\mathbb Q}_{\ell }} \simeq {\mathbb C}$ .

We prove the points (2) and (3) by explicit computations. As in Lemma 18, we denote by $\lambda ^t_a$ the partition $(1+a, 1^{2t-a})$ of $2t+1$ . Let $0\leq t \leq d$ . For $0\leq a \leq 2t$ , we will write

$$ \begin{align*} {\mathrm R}_{a}^{t} := {\mathrm R}_{L_{K_{t}}}^{{\mathrm U}_{2d+1}(q)}\left(\rho_{(d-t)}^{\mathrm{GL}}\boxtimes \rho^{{\mathrm U}}_{\lambda^{t}_{a}}\right). \end{align*} $$

Recall that Proposition 8 gives an isomorphism between the Ekedahl–Oort stratum $X_{I_t}(w_t)$ and the variety ${\mathrm U}_{2d+1}(q)/U_{K_{t}} \times _{L_{K_{t}}} X^{\mathbf L_{K_{t}}}_{I_{t}}(w_{t})$ . It implies that the cohomology of the Ekedahl–Oort stratum is the Harish-Chandra induction of the cohomology of the Deligne–Lusztig variety $X_{I_{t}}^{\mathbf L_{K_{t}}}(w_{t})$ . This cohomology is related to that of the Coxeter variety for ${\mathrm U}_{2t + 1}(q)$ . Combining with the formula of Proposition 19, for $0 \leq i \leq t - 1$ , it follows that

$$ \begin{align*} {\mathrm H}_c^{t + i}(X_{I_t}(w_t)) = {\mathrm R}_{2i}^{t} \oplus {\mathrm R}_{2i+1}^{t}, & & {\mathrm H}_c^{2t}(X_{I_t}(w_t)) = {\mathrm R}_{2t}^{t}. \end{align*} $$

The representation ${\mathrm R}_{a}^{t}$ in this formula is associated with the eigenvalue $(-q)^a$ of $F^2$ .

We first compute ${\mathrm R}_a^{t}$ explicitly. By the combination of the Comparison Theorem 12 and the Pieri rule for groups of type B as in Proposition 16, one can compute the Harish-Chandra induction ${\mathrm R}_a^{t}$ by adding $d-t$ boxes to the bipartition corresponding to the representation $\rho ^{{\mathrm U}}_{\lambda ^{t}_a}$ with no two added boxes in the same column. Recall from Lemma 18 that the representation $\rho _{\lambda _{2i}^{t}}$ of ${\mathrm U}_{2t+1}(q)$ is equivalent to the representation $\rho _{\Delta _1,(i),(1^{t-i})}$ , and that $\rho _{\lambda _{2i+1}^{t}}$ is equivalent to $\rho _{\Delta _2,(i),(1^{t-1-i})}$ .

In order to illustrate the argument, let us say that we want to add N boxes to a bipartition of the shape as in the figure below, so that no two added boxes lie in the same column.

We will add $N_1$ boxes to the first diagram and $N_2$ to the second, where $N = N_1 + N_2$ . In the first diagram, the only places where we can add boxes are in the second row from left to right, and at the end of the first row. Because no two added boxes must be in the same column, the number of boxes we add on the second row must be at most the number of boxes already lying in the first row. Of course, it must also be at most $N_1$ . In the second diagram, the only places where we can add boxes are at the bottom of the first column and at the end of the first row. Because no two added boxes must be in the same column, we can only put up to one box at the bottom of the first column and all the remaining ones will align at the end of the first row.

At the end of the process, we will obtain a bipartition of the following general shape.

We colored in yellow the boxes that were already there before we added new ones. The box with a question mark may or may not be placed there. We now make the result more precise, and write down exactly what the irreducible components of ${\mathrm R}_{a}^{t}$ are depending on the parity of a.

• – For $0\leq i \leq t$ , the representation ${\mathrm R}_{2i}^{t}$ is the multiplicity-free sum of all the representations $\rho _{\Delta _1,\alpha ,\beta }$ where the bipartition $(\alpha ,\beta )$ satisfies, for some $0 \leq x \leq d - t$ ,

  $$ \begin{align*}\begin{cases} \alpha = (i + x - s, s) \text{ for some } 0\leq s \leq \min(x,i),\\ \beta = (d - t - x, 1^{t - i}) \text{ or } (d - t - x + 1, 1^{t - i - 1}). \end{cases}\end{align*} $$

• – For $0\leq i \leq t - 1$ , the representation ${\mathrm R}_{2i+1}^{t}$ is the multiplicity-free sum of all representations $\rho _{\Delta _2,\alpha ,\beta }$ where the bipartition $(\alpha ,\beta )$ satisfies, for some $0 \leq x \leq d - t$ ,

  $$ \begin{align*}\begin{cases} \alpha = (i + x - s, s) \text{ for some } 0\leq s \leq \min(x,i),\\ \beta = (d - t + 1 - x, 1^{t - 1 - i}) \text{ or } (d - t + 2 - x, 1^{t - 2 - i}). \end{cases}\end{align*} $$

In our notations, we used the convention that the partitions $(0)$ and $(1^0)$ are the empty partition $\emptyset $ . The integer x corresponds to the number of boxes we add to the first partition. We notice that if i takes the maximal value, there is only one possibility for $\beta $ that is, respectively, $(d-t-x)$ in the first case and $(d - t + 1 - x)$ in the second case.

Recall from Proposition 7 that the variety $X_{I}(\mathrm {id})$ is the union of the Ekedahl–Oort strata $X_{I_t}(w_t)$ for $0\leq t \leq d$ and the closure of the stratum for t is the union of all strata $X_{I_s}(w_s)$ for $s \leq t$ . At the level of cohomology, it translates into the following $F^2,\mathrm {U}_{2d+1}(q)$ -equivariant spectral sequence:

$$ \begin{align*}\mathrm E_1^{t,i} : {\mathrm H}_c^{t+i}(X_{I_t}(w_t)) \implies {\mathrm H}_c^{t+i}(X_{I}(\mathrm{id})).\end{align*} $$

The first page of the sequence is drawn in Figure 1, and it has a triangular shape.

Figure 1 The first page of the spectral sequence.

The representation ${\mathrm R}^{t}_{a}$ corresponds to the eigenvalue $(-q)^a$ of $F^2$ as before. The only eigenvalues of $F^2$ on the ith row of the spectral sequence are $q^{2i}$ and $-q^{2i+1}$ . In particular, the eigenvalues on two distinct rows are different. Since the differentials in deeper pages of the sequence map terms from different rows, their $F^2$ -equivariance implies that they vanish. Therefore, the sequence degenerates on the second page. Moreover, by the machinery of spectral sequences, for $0\leq k \leq 2d$ , there exists a filtration by $\mathrm {U}_{2d+1}(q)\times \langle F^2 \rangle $ -modules on ${\mathrm H}_c^{k}(X_{I}(\mathrm {id}))$ whose graded components are the terms of the second page lying on the anti-diagonal $t+i=k$ . Since the group algebra $\overline {{\mathbb Q}_{\ell }}[\mathrm {U}_{2d+1}(q)]$ is semi-simple, the filtration splits, meaning that ${\mathrm H}_c^{k}(X_{I}(\mathrm {id}))$ is actually the direct sum of the graded components. The purity of ${\mathrm H}_c^{k}(X_{I}(\mathrm {id}))$ then implies that all the terms of the second page lying on the antidiagonal $t+i = k$ , which are associated with an eigenvalue whose modulus is not equal to $q^k$ , must be zero. Therefore, the second page has the shape described in Figure 2. The Frobenius $F^2$ acts via $q^{2i}$ on the term $\mathrm E_2^{i,i}$ , and via $-q^{2i+1}$ on the term $\mathrm E_2^{i+1,i}$ . Point (2) of the theorem readily follows.

Figure 2 The second page of the spectral sequence.

By the previous computations, we understand precisely all the terms in the first page of the spectral sequence. The key observation to compute the second page is that two terms on the first page, which lie on the same row, but are separated by at least two arrows, do not have any irreducible component in common. We make the argument more precise in the following two paragraphs, distinguishing the cohomology groups of even and odd index.

We first compute the cohomology group ${\mathrm H}_{c}^{2t}(X_{I}(\mathrm {id}))$ for $0\leq t \leq d$ . We look at the following portion of the first page:

By extracting the eigenspaces corresponding to $q^{2t}$ , we actually have the following sequence:

The representation ${\mathrm R}^{t}_{2t}$ is the sum of all the representations $\rho _{\Delta _1,\alpha ,\beta }$ where for some $0\leq x \leq d - t$ and for some $0\leq s \leq \min (x,t)$ , we have $\alpha = (t + x - s, s)$ and $\beta = (d - t - x)$ .

The representation ${\mathrm R}^{t+1}_{2t}$ is the sum of all the representations $\rho _{\Delta _1,\alpha ',\beta '}$ where for some $0\leq x' \leq d - t - 1$ and for some $0\leq s \leq \min (x',t)$ , we have $\alpha ' = (t + x' - s, s)$ and $\beta ' = (d - t - x')$ or $(d - t - x' - 1, 1)$ .

The quotient space $\mathrm {Ker}(v)/\mathrm {Im}(u)$ is isomorphic to the eigenspace of $q^{2t}$ in $E_{2}^{t+1,t}$ , which is zero. In addition, in the representation ${\mathrm R}^{t+2}_{2t}$ , all the irreducible components have the shape $\rho _{\Delta _1,\alpha ",\beta "}$ with $\beta "$ a partition of length $2$ or $3$ . In particular, all the representations $\rho _{\Delta _1,\alpha ',\beta '}$ of ${\mathrm R}^{t+1}_{2t}$ with $\beta '$ a partition of length $1$ automatically lie inside $\mathrm {Ker}(v) = \mathrm {Im}(u)$ . Such representations correspond to all the irreducible components $\rho _{\Delta _1,\alpha ,\beta }$ of ${\mathrm R}^{t}_{2t}$ having $x \not = d - t$ . Thus, none of them lies in $\mathrm {Ker}(u) \simeq E_2^{t,t}$ .

The remaining components of ${\mathrm R}^{t}_{2t}$ are those having $x = d - t$ , and they do not occur in the codomain of u so that they lie in $\mathrm {Ker}(u)$ . By the previous argument, they must form the whole of $\mathrm {Ker}(u)$ . Thus, we have proved that

$$ \begin{align*} E_2^{t,t} \simeq {\mathrm H}_{c}^{2t}(X_{I}(\mathrm{id})) \simeq \mathrm{Ker}(u) = \bigoplus_{s = 0}^{\min(t,d-t)} \rho_{\Delta_1,(t-s,s),\emptyset} \end{align*} $$

and it coincides with the formula of point (3).

We now compute the cohomology group ${\mathrm H}_{c}^{2t+1}(X_{I}(\mathrm {id}))$ for $0\leq t \leq d-1$ . We look at the following portion of the first page:

By extracting the eigenspaces corresponding to $-q^{2t+1}$ , we actually have the following sequence:

The representation ${\mathrm R}^{t+1}_{2t+1}$ is the sum of all the representations $\rho _{\Delta _2,\alpha ,\beta }$ where for some $0\leq x \leq d - t - 1$ and for some $0\leq s \leq \min (x,t)$ , we have $\alpha = (t + x - s,s)$ and $\beta = (d - t - x)$ .

The representation ${\mathrm R}^{t+2}_{2t+1}$ is the sum of all the representations $\rho _{\Delta _2,\alpha ',\beta '}$ where for some $0\leq x' \leq d - t - 2$ and for some $0\leq s \leq \min (x',t)$ , we have $\alpha ' = (t + x' -s,s)$ and $\beta ' = (d - t - 1 - x', 1)$ or $(d - t - x')$ .

The quotient space $\mathrm {Ker}(v)/\mathrm {Im}(u)$ is isomorphic to the eigenspace of $-q^{2t+1}$ in $E_{2}^{t+2,t}$ , which is zero. In addition, in the representation ${\mathrm R}^{t+3}_{2t+1}$ , all the irreducible components have the shape $\rho _{\Delta _2,\alpha ",\beta "}$ with $\beta "$ a partition of length $2$ or $3$ . In particular, all the representations $\rho _{\Delta _2,\alpha ',\beta '}$ of ${\mathrm R}^{t+2}_{2t+1}$ with $\beta '$ a partition of length $1$ automatically lie inside $\mathrm {Ker}(v) \simeq \mathrm {Im}(u)$ . Such representations correspond to all the irreducible components $\rho _{\Delta _2,\alpha ,\beta }$ of ${\mathrm R}^{t+1}_{2t+1}$ having $x \not = d - t - 1$ . Thus, none of them lies in $\mathrm {Ker}(u) \simeq E_2^{t+1,t}$ .

The remaining components of ${\mathrm R}^{t+1}_{2t+1}$ are those having $x = d - t - 1$ , and they do not occur in the codomain of u so that they lie in $\mathrm {Ker}(u)$ . By the argument above, they must form the whole of $\mathrm {Ker}(u)$ . Thus, we have proved that

$$ \begin{align*} E_2^{t+1,t} \simeq {\mathrm H}_{c}^{2t+1}(X_{I}(\mathrm{id})) \simeq \mathrm{Ker}(u) = \bigoplus_{s = 0}^{\min(d-t-1, t)} \rho_{\Delta_2,(t-1-s,s),\emptyset}, \end{align*} $$

and one may check that it coincides with the formula of point (3).