COEFFICIENT QUIVERS, 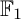${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS

Abstract

A quiver representation assigns a vector space to each vertex, and a linear map to each arrow of a quiver. When one considers the category 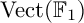$\mathrm {Vect}(\mathbb {F}_1)$ of vector spaces “over 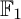$\mathbb {F}_1$” (the field with one element), one obtains 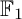$\mathbb {F}_1$-representations of a quiver. In this paper, we study representations of a quiver over the field with one element in connection to coefficient quivers. To be precise, we prove that the category 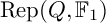$\mathrm {Rep}(Q,\mathbb {F}_1)$ is equivalent to the (suitably defined) category of coefficient quivers over Q. This provides a conceptual way to see Euler characteristics of a class of quiver Grassmannians as the number of “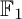$\mathbb {F}_1$-rational points” of quiver Grassmannians. We generalize techniques originally developed for string and band modules to compute the Euler characteristics of quiver Grassmannians associated with 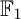$\mathbb {F}_1$-representations. These techniques apply to a large class of 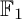$\mathbb {F}_1$-representations, which we call the 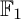$\mathbb {F}_1$-representations with finite nice length: we prove sufficient conditions for an 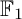$\mathbb {F}_1$-representation to have finite nice length, and classify such representations for certain families of quivers. Finally, we explore the Hall algebras associated with 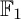$\mathbb {F}_1$-representations of quivers. We answer the question of how a change in orientation affects the Hall algebra of nilpotent 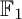$\mathbb {F}_1$-representations of a quiver with bounded representation type. We also discuss Hall algebras associated with representations with finite nice length, and compute them for certain families of quivers.

1 Introduction

Mathematics over the field with one element ${\mathbb {F}}_1$ is a recent area of research that draws primarily from considerations in algebraic geometry, number theory, and combinatorics. The term field of characteristic one was originally coined by J. Tits. In [31], Tits observed that incidence geometries over a finite field ${\mathbb {F}}_q$ have a combinatorial counterpart ¹ which could be interpreted as incidence geometries defined over the field of characteristic one.

In [26], Soulé first introduced the notion of algebraic varieties over the field with one element (denoted by ${\mathbb {F}}_1$ ) by taking the functor of points approach, and suggested several research directions to pursue. Soulé also asked whether or not Chevalley group schemes G could be defined over ${\mathbb {F}}_1$ in such a way as to relate the set $G({\mathbb {F}}_1)$ of ${\mathbb {F}}_1$ -rational points to the Weyl group $W_G$ of G. In [3], Connes and Consani provided a positive answer to the question posed by Soulé. This question was further studied by Lorscheid [19] by using the algebraic structure of a blueprint (see [18] for blueprints).

One heuristic idea of ${\mathbb {F}}_1$ -geometry is that when an algebraic variety X over $\mathbb {Z}$ has an ${\mathbb {F}}_1$ -model $X_{{\mathbb {F}}_1}$ , then the number of ${\mathbb {F}}_1$ -rational points of $X_{{\mathbb {F}}_1}$ should be the Euler characteristic of $X(\mathbb {C})$ . ² The heuristic is essentially based on the relation between the counting function of $X({\mathbb {F}}_q)$ and the Euler characteristic of $X(\mathbb {C})$ for a smooth projective scheme X. For example, the cardinality of the set of ${\mathbb {F}}_q$ -rational points of the Grassmannian $\mathrm {Gr}(k,n)$ is given by the q-binomial coefficients:

(1.1) $$ \begin{align} |\mathrm{Gr}(k,n)({\mathbb{F}}_q)|=\begin{bmatrix} n \\ k \end{bmatrix}_q, \end{align} $$

and by evaluating (1.1) at $q=1$ , we obtain

(1.2) $$ \begin{align} {n\choose k} = \chi (\mathrm{Gr}(k,n)(\mathbb{C})), \end{align} $$

the Euler characteristic of $\mathrm {Gr}(k,n)(\mathbb {C})$ . ³ We refer the reader to [18, §4] for more details.

Quiver Grassmannians are projective varieties whose points parameterize certain subrepresentations of a given quiver representation. The usual Grassmannians can be recovered by taking the quiver to have a single vertex and no arrows. In [23], Reineke showed that any projective variety is a quiver Grassmannian. In particular, the class of quiver Grassmannians is not just a special class of projective varieties, but they are all projective varieties. What is more surprising is the result of Ringel [25], which shows that there exists a single quiver Q (independent of a projective variety) such that for a given projective variety X, one can find a representation M of Q and a dimension vector $\mathbf {e}$ such that $X=\operatorname {Gr}^Q_{\mathbf {e}}(M)$ , the quiver Grassmannian of $\mathbf {e}$ -dimensional subrepresentations of M:

$$ \begin{align*} \mathrm{Gr}^Q_{\mathbf{e}}(M):=\{N \leq M \mid \mathbf{{dim}}(N)=\mathbf{e}\}. \end{align*} $$

We refer the reader to [2] for further results.

Let Q be a finite quiver throughout. Lorscheid has proved that if M admits a basis in which the arrows of Q act via integer matrices, then $\operatorname {Gr}^Q_{\mathbf {{e}}}(M)$ admits an $\mathbb {F}_1$ -model [18]. If M is a tree module, it can be proved that the Euler characteristic of $\operatorname {Gr}^Q_{\mathbf {{e}}}(M)$ counts the number of ${\mathbb {F}}_1$ -rational points. Cerulli Irelli computes the Euler characteristic of $\operatorname {Gr}^Q_{\mathbf {e}}(M)$ when M is a string module in [1]. Haupt extends this work to tree modules, and produces results of a similar flavor for band modules [7]. For some tree modules and modules over certain tame quivers, Lorscheid and Weist develop techniques for computing Schubert decompositions of quiver Grassmannians which can be used to compute their Euler characteristics [16], [17], [20]–[22]. It is therefore natural to pose the following questions, following Lorscheid.

Question 1.1 (cf. [18])

1. 1. If M is such that $\operatorname {Gr}^Q_{\mathbf {e}}(M)$ admits an ${\mathbb {F}}_1$ -model, what conditions on M guarantee that the Euler characteristic of $\operatorname {Gr}^Q_{\mathbf {e}}(M)$ counts its number of ${\mathbb {F}}_1$ -rational points?

2. 2. If the number of ${\mathbb {F}}_1$ -rational points of $\operatorname {Gr}^Q_{\mathbf {e}}(M)$ is given by its Euler characteristic, can one find an efficient combinatorial formula for computing it?

In this paper, we partially provide an affirmative answer to Question 1.1. We begin with the ${\mathbb {F}}_1$ -representations of Q, first introduced by Szczesny in [27] and studied further by the authors in [10] using the coefficient quivers of Ringel [24]. Using the combinatorial techniques developed in [7], we describe a class of ${\mathbb {F}}_1$ -representations whose associated quiver Grassmannians admit filtrations by locally closed subsets, each of which is the fixed point set of a torus action on the previous one, and whose last piece is finite. We show that this class, which we call the ${\mathbb {F}}_1$ -representations with finite nice length, contains many of the representations considered in [1], [7] as well as new ones. In addition to exhibiting new representations, we show that the class of ${\mathbb {F}}_1$ -representations with finite nice length includes representations whose coefficient quivers have first homology groups with arbitrarily high rank. Taken together, this demonstrates that the basic techniques of [1], [7] can be successfully applied to a broad class of representations beyond those previously considered in the literature.

Szczesny explored several aspects of representation theory over ${\mathbb {F}}_1$ in [11], [28]–[30]. In particular, he introduced a notion of quiver representations over ${\mathbb {F}}_1$ based on an idea that vector spaces over ${\mathbb {F}}_1$ are finite pointed sets. To be precise, to define an ${\mathbb {F}}_1$ -representation of a quiver Q, one may replace vector spaces with finite pointed sets ( ${\mathbb {F}}_1$ -vector spaces) and linear maps with pointed functions satisfying an injectivity condition ( ${\mathbb {F}}_1$ -linear maps). This defines the category $\mathrm {Rep}(Q,{\mathbb {F}}_1)$ of ${\mathbb {F}}_1$ -representations of Q, which can be considered as a degenerate combinatorial model of the category $\mathrm {Rep}(Q,{\mathbb {F}}_q)$ . In fact, Szczesny’s main observation was that the Hall algebra $H_{Q,{\mathbb {F}}_1}$ of $\mathrm {Rep}(Q,{\mathbb {F}}_1)$ behaves in some ways like the specialization at $q=1$ of the Hall algebra $H_{Q,{\mathbb {F}}_q}$ of $\mathrm {Rep}(Q,{\mathbb {F}}_q)$ . ⁴ This line of ideas was further pursued with the first named author in [11] to compute the Hall algebra of coherent sheaves on $\mathbb {P}^2$ by using its degenerate combinatorial model of monoid schemes.

In our recent work [10], we stratified quivers according to the asymptotic growth of their indecomposable nilpotent ${\mathbb {F}}_1$ -representations. To this end, we defined the growth function $\operatorname {NI}_Q:\mathbb {N} \to \mathbb {Z}_{\geq 0}$ such that

$$ \begin{align*} \operatorname{NI}_Q(n) := \#\{\text{isoclasses of}\ n\text{-dimensional nilpotent indecomposables in }{\operatorname{Rep}}(Q,{\mathbb{F}}_1) \}. \end{align*} $$

Then we used the growth function to define an order relation among quivers: for two quivers Q and $Q'$ , write $Q \le _{{\operatorname {nil}}} Q'$ if there exists a natural number C such that $\operatorname {NI}_Q = O(\operatorname {NI}_{Q'} \circ \mu _C)$ in big-O notation, where $\mu _C$ is a multiplication function by C. This order relation induces an equivalence relation $\approx _{{\operatorname {nil}}}$ on quivers as follows:

$$ \begin{align*} Q \approx_{{\operatorname{nil}}} Q' \iff Q \le_{{\operatorname{nil}}} Q'\ \mathrm{and}\ Q' \le_{{\operatorname{nil}}} Q. \end{align*} $$

In [10], we proved the following:

Theorem [10]

Let ${\mathbb {L}}_n$ be the quiver with one vertex and n-loops, and let Q be connected.

1. (i) ${\mathbb {L}}_0,{\mathbb {L}}_1,{\mathbb {L}}_2$ are not equivalent to each other, and ${\mathbb {L}}_m \approx _{{\operatorname {nil}}} {\mathbb {L}}_n$ whenever $\min \{m,n\} \geq 2$ .

2. (ii) $Q \approx _{{\operatorname {nil}}} {\mathbb {L}}_0$ if and only if Q is a tree quiver.

3. (iii) $Q \approx _{{\operatorname {nil}}} {\mathbb {L}}_1$ if and only if Q is a cycle quiver.

4. (iv) For any quiver Q, one has $Q \le _{{\operatorname {nil}}} {\mathbb {L}}_2$ .

When S is a coefficient quiver of Q, one naturally obtains a quiver map $F:S \to Q$ satisfying some conditions. The class of quiver maps satisfying this condition, called windings, was studied by Gabriel [6], Crawley-Boevey [4], Krause [15], and Haupt [7]. More explicitly, a winding is a morphism of quivers $F:S\to Q$ consisting of a pair of functions ⁵

$$ \begin{align*} F_0:S_0 \to Q_0, \quad F_1:S_1 \to Q_1 \end{align*} $$

satisfying the following condition:

$$ \begin{align*} F_1(\alpha)=F_1(\beta)\ \mathrm{implies}\ s(\alpha) \neq s(\beta)\ \mathrm{and}\ t(\beta) \neq t(\beta), \end{align*} $$

where $s(\alpha )$ (resp. $t(\alpha )$ ) is the source (resp. target) of an arrow $\alpha $ . We consider the category $\mathcal {C}_Q$ of quivers over a quiver Q as follows: Let $\mathcal {C}_Q$ be the category whose objects are windings of quivers $F:S \to Q$ . A morphism $\phi : (S,F)\rightarrow (S',F')$ is an ordered triple $\phi = (\mathcal {U}_{\phi }, \mathcal {D}_{\phi }, c_{\phi })$ satisfying some technical conditions, where $\mathcal {U}_{\phi }$ is a full subquiver of S, $\mathcal {D}_{\phi }$ is a full subquiver of $S'$ , and $c_{\phi } : \mathcal {U}_{\phi } \rightarrow \mathcal {D}_{\phi }$ is a quiver isomorphism. We first upgrade the correspondence between coefficient quivers and ${\mathbb {F}}_1$ -representations in [10] to the categorical equivalence as follows.

Theorem A (Proposition 3.7)

The categories $\text {Rep}(Q,{\mathbb {F}}_1)$ and $\mathcal {C}_Q$ are equivalent. This restricts to an equivalence between ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}$ and the full subcategory of $\mathcal {C}_Q$ whose objects are windings $F:S \to Q$ with S acyclic.

The above theorem also provides a conceptual framework to compute the Euler characteristic of a quiver Grassmannian through a base-change functor. To be precise, one always obtains a representation of Q over $\mathbb {C}$ from a representation of Q over ${\mathbb {F}}_1$ functorially as follows: a finite pointed set V defines a vector space $V_{\mathbb {C}}$ whose basis is $V-\{0_V\}$ . This induces a functor for quiver representations:

$$ \begin{align*} \mathbb{C}\otimes_{{\mathbb{F}}_1}-:\mathrm{Rep}(Q,{\mathbb{F}}_1) \to \mathrm{Rep}(Q,\mathbb{C}), \quad M \mapsto M_{\mathbb{C}}. \end{align*} $$

This functor is always faithful, but generally not full (cf. the example at the end of [15]).

The methods of Cerulli Irelli and Haupt to compute Euler characteristics of quiver Grassmannians are based on the following idea: that when a projective variety X is equipped with a torus action admitting a finite number of fixed points, one may compute the Euler characteristic $\chi (X)$ of X as the number of fixed points by the torus action. To ensure the existence of a torus action, Cerulli Irelli introduced a certain condition for string modules. This idea was generalized by Haupt by introducing a notion of gradings on representations. We show that Haupt’s definition applies to ${\mathbb {F}}_1$ -representations of quivers.

For an ${\mathbb {F}}_1$ -representation M of Q and its corresponding winding $\Gamma _M \to Q$ (from Theorem A), we define a nice sequence on M to be a collection $\underline {\partial } = ( \partial _i)_{i \geq 0}$ of functions $\partial _i : (\Gamma _M)_0 \rightarrow \mathbb {Z}$ satisfying the following two conditions: ⁶

1. 1. $\partial _0$ is a nice grading.

2. 2. For all $i>0$ , $\partial _i$ is a $(\partial _0,\ldots , \partial _{i-1})$ -nice grading.

See §4 or [7] for the terminology on gradings. If there exists a nice sequence $\underline {\partial } = ( \partial _i)_{i\geq 0}$ on M with the property that for all distinct $x,y\in (\Gamma _M)_0$ , $\partial _i(x) \neq \partial _i(y)$ for some $i\geq 0$ , then Haupt proves in [7] that the following formula holds for all dimension vectors $\mathbf {e}$ :

(1.3) $$ \begin{align} \chi_{\mathbf{e}}^Q(M_{\mathbb{C}}) = |\{ N \le M \mid \mathbf{{dim}}(N) = \mathbf{e} \}|, \end{align} $$

where $\chi ^Q_{\mathbf {e}}(M_{\mathbb {C}})$ is the Euler characteristic of $\mathrm {Gr}^Q_{\mathbf {e}}(M_{\mathbb {C}})$ . In other words, the Euler characteristics of the associated quiver Grassmannians can all be computed by counting ${\mathbb {F}}_1$ -subrepresentations of M, which is a combinatorial task. See Proposition 5.2 below for more details. We say that M has finite nice length in this case: specifically, we say $\operatorname {nice}(M) = n$ if there exists a nice sequence $\underline {\partial }$ for M such that each pair of vertices in $\Gamma _M$ can be distinguished by the first $n+1$ gradings (and $\operatorname {nice}(M) = \infty $ otherwise). More generally, if (1.3) holds for all dimension vectors $\mathbf {e}$ , we say that M is nice. Our task is then to identify all nice ${\mathbb {F}}_1$ -representations of a given quiver, or at least the ${\mathbb {F}}_1$ -representations with finite nice length.

In Construction 4.12, we generalize notions from [7] to test for the existence of nice sequences with prescribed properties. To any indecomposable ${\mathbb {F}}_1$ -representation M, we construct a sequence of finitely generated free abelian groups $\mathcal {V}^{(i)}_M$ . For each i, we then define a function

$$ \begin{align*} X^{(i)} : (\Gamma_M)_0 \rightarrow \mathcal{V}^{(i)}_M \end{align*} $$

$$ \begin{align*} v \mapsto X^{(i)}_v \end{align*} $$

called the universal i-nice grading on M. The image of v under $X^{(i)}$ is called the i-nice variable associated with v. The universal i-nice grading is only unique up to translation, but this is easily dealt with by specifying a basepoint $b \in (\Gamma _M)_0$ . The name of this function is justified by the following theorem.

Theorem B (Theorem 4.19)

Let M be an indecomposable ${\mathbb {F}}_1$ -representation of Q, with associated winding $c : \Gamma \rightarrow Q$ and basepoint $b \in \Gamma _0$ . Let $\underline {\partial } = (\partial _i)_{i=0}^{\infty }$ be a nice sequence for M. Then, for each i, there exists a unique affine map

$$ \begin{align*} \operatorname{ev}^{(i)}(\underline{\partial}) : \mathcal{V}^{(i)}_M \rightarrow \mathbb{Z} \end{align*} $$

such that $\partial _i = \operatorname {ev}^{(i)}(\underline {\partial }) \circ X^{(i)}$ . We write $X^{(i)}(\underline {\partial }) := \operatorname {ev}^{(i)}(\underline {\partial }) \circ X^{(i)}$ and call it the evaluation of $X^{(i)}$ at $\underline {\partial }$ . Conversely, any such sequence of affine maps defines a nice sequence on M.

As a consequence, we have $\partial _i(u) \neq \partial _i(v)$ for some nice sequence $\underline {\partial }$ if and only if $X^{(i)}_u \neq X^{(i)}_v$ .

In §5, we apply the machinery of §4 to identify representations with finite nice length. To begin, we prove several sufficient conditions for M to have finite nice length (see §§4 and 5 for all associated terminology):

Theorem C (Propositions 5.7 and 5.8)

Let Q be a quiver and M an indecomposable ${\mathbb {F}}_1$ -representation of Q with associated winding $c : \Gamma \rightarrow Q$ . Then the following statements hold:

1. 1. Suppose that M admits a positive or negative nice grading, and that Q has no loops. If for each $\alpha \in Q_1$ , $\partial $ restricts to an injection on the set $\{s(\beta ) \mid \beta \in \Gamma _1, c(\beta ) =\alpha \}$ , then $\operatorname {nice}(M) \le 1$ and M is nice.

2. 2. Suppose that M admits a non-degenerate grading, and that for all $\alpha \in Q_1$ , the minimal subquiver of $\Gamma $ containing the arrows $\{ \beta \in \Gamma _1 \mid c(\beta ) = \alpha \}$ is connected. Then $\operatorname {nice}(M)\le 1$ .

3. 3. Suppose that N is another indecomposable representation of Q, with associated winding $c' : \Gamma ' \rightarrow Q$ . Suppose that $c(\Gamma )$ and $c'(\Gamma ')$ have disjoint arrow sets, and that there exist vertices $u \in \Gamma _0$ and $v \in \Gamma ^{\prime }_0$ with $c(u) = c'(v)$ . If $\operatorname {nice}(M)<\infty $ and $\operatorname {nice}(N)<\infty $ , then the ${\mathbb {F}}_1$ -representation associated with the amalgam $c\sqcup _{u\sim v}c' : \Gamma \sqcup _{u\sim v}\Gamma ' \rightarrow Q$ has finite nice length.

We then exhibit a nontrivial class of representations which satisfy $\operatorname {nice}(M) \le 1$ . In general, this class of representations will have nice length $1$ , and coefficient quivers that are neither trees nor affine Dynkin quivers of type $\tilde {\mathbb {A}}$ . In particular, this class contains representations different than the cases considered in [1], [7]:

Theorem D (Proposition 5.9)

Let M be a nilpotent ${\mathbb {F}}_1$ -representation of a quiver Q with associated winding $c: \Gamma \rightarrow Q$ . Suppose that $c^{-1}(\alpha )$ is connected for all $\alpha \in Q_1$ , and that $\Gamma $ contains a set of $\mathbb {Z}$ -linearly independent cycles $\{ X_1,\ldots , X_n\}$ with the following properties:

1. (i) The cycles $[\iota \circ H_1(c)](X_1)$ , $\ldots , [\iota \circ H_1(c)](X_n)$ form a $\mathbb {Q}$ -basis for $\mathbb {Q}\otimes _{\mathbb {Z}}\operatorname {Im}(\iota \circ H_1(c))$ , where $\iota \circ H_1(c)$ is as in (4.15).

2. (ii) For all i, we can write $X_i = p_i - q_i$ , where $p_i$ and $q_i$ are directed paths of positive length in $\Gamma $ with common source and target, but no interior vertices in common.

3. (iii) For each $i\le n$ , either $c(p_i)$ or $c(q_i)$ consists of arrows that do not appear in $c(X_j)$ for $j \neq i$ , where we consider $c(X_j)$ as a subquiver of Q.

Then $\operatorname {nice}(M)\le 1$ and M is nice.

We illustrate the above results with several examples. Furthermore, we patch apparent gaps in the proofs of Lemmas 6.3 and 6.4 in [7], at least for the case of ${\mathbb {F}}_1$ -representations. We outline the gaps we believe we have uncovered in the Appendix to this article, and explain how our results resolve them. It should be noted that the class of ${\mathbb {F}}_1$ -representations with finite nice length contains representations which have been previously studied in the literature, in addition to the new ones described above. Special cases include the following: the ${\mathbb {F}}_1$ -representations satisfying the conditions of Theorem 1 in [1], which are recovered as the ${\mathbb {F}}_1$ -representations with nice length $0$ ; the ${\mathbb {F}}_1$ -representations whose coefficient quiver is a tree, correcting the proof of [7, Lem. 6.3]; and the ${\mathbb {F}}_1$ -representations whose coefficient quiver is a primitive affine Dynkin quiver of type $\tilde {\mathbb {A}}$ , recovering a special case of [7, Lem. 6.4]. These cases cover all ${\mathbb {F}}_1$ -representations with finite nice length when Q is a pseudotree, but not in general. We summarize these remarks with the following theorem.

Theorem E (cf. [1, Th. 1], [7, Lems. 6.3 and 6.4])

Let Q be a quiver, and for each $n \in \mathbb {N}$ , let $I_{Q,{\operatorname {nil}}}^{n}$ denote the set of isomorphism classes of finite-dimensional indecomposable, nilpotent ${\mathbb {F}}_1$ -representations of Q with nice length n. Furthermore, let $I_{Q,{\operatorname {nil}}}^{\operatorname {nice}} = \bigcup _{n \in \mathbb {N}}{I_{Q,{\operatorname {nil}}}^{n}}$ . Then the following hold:

1. 1. $M \in I_{Q,{\operatorname {nil}}}^0$ if and only if M admits a nice grading $\partial $ that restricts to an injection on $c_M^{-1}(v)$ , for all $v \in Q_0$ .

2. 2. If the coefficient quiver of M is a tree, then $M \in I_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ . In general, $M \not \in I_{Q,{\operatorname {nil}}}^0$ .

3. 3. If the coefficient quiver of M is an affine Dynkin quiver of type $\tilde {\mathbb {A}}$ , then $M \in I_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ if and only if the associated winding $c_M : \Gamma _M \rightarrow Q$ is primitive. In general, $M \not \in I_{Q,{\operatorname {nil}}}^0$ .

If Q is a (not necessarily proper) pseudotree, then every $M \in I_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ belongs to at least one of the three cases described above. If $Q = {\mathbb {L}}_n$ with $n\geq 2$ , then $I_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ contains ${\mathbb {F}}_1$ -representations that do not belong to any of the these three cases.

Case (1) is discussed in Example 5.5. Case (2) is discussed in Corollary 5.18, and case (3) is discussed in Theorem 5.20. Examples of representations with strictly positive nice length are discussed throughout §§4 and 5. The results on pseudotrees follow readily from Corollary 6.11 and the classification of nilpotent indecomposable ${\mathbb {F}}_1$ -representations for bounded type given in [10]. Finally, explicit examples for ${\mathbb {L}}_2$ and ${\mathbb {L}}_3$ are computed in §5.

In §6, we turn our attention to the Hall algebras $H_Q$ and $H_{Q,{\operatorname {nil}}}$ of ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ and ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}$ . Recall that $H_Q$ and $H_{Q,{\operatorname {nil}}}$ are graded, connected, cocommutative Hopf algebras: by the Milnor–Moore theorem, they are isomorphic to the universal enveloping algebras of their Lie subalgebras of primitive elements. Throughout, we denote the Lie algebra of $H_{Q,{\operatorname {nil}}}$ by $\mathfrak {n}_Q$ . Motivated by a question from [27], in §6.1, we study how a change in the orientation of Q affects $H_{Q,{\operatorname {nil}}}$ . We obtain the following results for quivers of bounded representation type.

Theorem F. Let Q be a quiver, with $\mathfrak {n}_Q$ the Lie algebra of primitive elements in $H_{Q,{\operatorname {nil}}}$ . Let $Q'$ be a quiver with the same underlying graph as Q.

1. 1. (Proposition 6.3) If Q and $Q'$ are trees, then $\mathfrak {n}_Q \cong \mathfrak {n}_{Q'}$ as Lie algebras.

2. 2. (Proposition 6.7) Suppose that $Q'$ is an equioriented affine Dynkin quiver of type $\tilde {\mathbb {A}}_n$ . Then $\mathfrak {n}_Q$ is a central extension of $\mathfrak {n}_{Q'}$ .

Note that Szczesny computed $\mathfrak {n}_Q$ in the case that Q is an equioriented $\tilde {\mathbb {A}}_n$ in [27]. Finally, in §6.2, we construct Hall algebras associated with representations of finite nice length and identify them in specific instances. Indeed, consider the full subcategories ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)^{\operatorname {nice}}$ and ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}^{\operatorname {nice}}$ of ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ and ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}$ whose objects M satisfy $\operatorname {nice}(M)<\infty $ . These categories are finitary and proto-exact, and so one can associate Hall algebras $H_Q^{\operatorname {nice}}$ and $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ . We prove the following theorem, which relates $H_Q$ (resp. $H_{Q,{\operatorname {nil}}}$ ) to $H_Q^{\operatorname {nice}}$ (resp. $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ ).

Theorem G (Proposition 6.8)

Let Q be a quiver. Then the $\mathbb {C}$ -subspaces

$$ \begin{align*} I=\langle [M] \mid \operatorname{nice}(M) = \infty \rangle, \end{align*} $$

$$ \begin{align*} I_{{\operatorname{nil}}}=\langle [M] \mid M\text{ is nilpotent and } \operatorname{nice}(M) = \infty \rangle \end{align*} $$

are Hopf ideals in $H_Q$ and $H_{Q,{\operatorname {nil}}}$ , respectively. We have Hopf algebra isomorphisms $H_Q/I \cong H_Q^{\operatorname {nice}}$ and $H_{Q,{\operatorname {nil}}}/I_{{\operatorname {nil}}} \cong H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ .

This allows us to identify $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ in the case that Q is a (not-necessarily proper) pseudotree. Specific formulas can be found in Corollaries 6.10 and 6.12. We can also give the following, more conceptual interpretation to our results. We say that an ${\mathbb {F}}_1$ -representation M is absolutely indecomposable if $k\otimes _{{\mathbb {F}}_1}M$ is indecomposable for every algebraically closed field k.

Theorem H (Corollaries 6.10–6.12)

Let Q be a (not-necessarily proper) pseudotree. Then the following statements hold. ⁷

1. 1. Let Q be of bounded representation type over ${\mathbb {F}}_1$ . Then $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ has a generating set that may be naturally identified with the absolutely indecomposable ${\mathbb {F}}_1$ -representations of Q.

2. 2. Let Q be a proper pseudotree with central cycle C. Then $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ has a generating set that may be naturally identified with the indecomposable ${\mathbb {F}}_1$ -representations M such that ${\operatorname {Res}}_C(M)$ is absolutely indecomposable.

2 Preliminaries

2.1 Representations of quivers over ${\mathbb {F}}_1$

In this section, we review basic definitions and properties of representations of quivers over ${\mathbb {F}}_1$ . We first recall the definition of ${\mathbb {F}}_1$ -vector spaces and ${\mathbb {F}}_1$ -linear maps.

Definition 2.1. The category $\mathrm {Vect}(\mathbb {F}_1)$ of finite-dimensional vector spaces over $\mathbb {F}_1$ consists of the following:

1. 1. Objects are finite pointed sets $(V,0_V)$ , called ${\mathbb {F}}_1$ -vector spaces.

2. 2. Morphisms are pointed functions $\varphi :V \to W$ such that $\varphi |_{V-\varphi ^{-1}(0_W)}$ is an injection, called ${\mathbb {F}}_1$ -linear maps.

For an $\mathbb {F}_1$ -vector space V, the dimension of V, denoted by $\dim _{{\mathbb {F}}_1}(V)$ , is the number of nonzero elements of V. In other words, $\dim _{{\mathbb {F}}_1}(V)=|V|-1$ .

Definition 2.2. Let V and W be $\mathbb {F}_1$ -vector spaces.

1. 1. The direct sum $V\oplus W$ is the following ${\mathbb {F}}_1$ -vector space: $V\oplus W:=V\sqcup W /\langle 0_V \sim 0_W\rangle $ .

2. 2. A unique $\mathbb {F}_1$ -linear map $0: V \to W$ sending any element in V to $0_W$ is said to be the zero map.

3. 3. W is said to be a subspace of V if W is a subset of V containing $0_V$ and $0_W=0_V$ .

4. 4. For a subspace W of V, the quotient space $V/W$ is defined as $V-(W-\{0_V\})$ .

5. 5. For an $\mathbb {F}_1$ -linear map $\varphi :V \to W$ , the kernel (resp. cokernel) of $\varphi $ is defined to be $\ker (\varphi ):=\varphi ^{-1}(0_W)$ (resp. $\mathrm {coker}(\varphi ):=W/\varphi (V)$ ).

Definition 2.3. A quiver Q is a finite directed graph, where we allow multiple arrows and loops. To be precise, a quiver Q consists of a quadruple $Q=(Q_0,Q_1,s,t)$ as follows:

1. 1. $Q_0$ (resp. $Q_1$ ) is the finite set of vertices (resp. arrows).

2. 2. s and t are functions

   $$ \begin{align*} s,t:Q_1 \to Q_0 \end{align*} $$
   assigning to each arrow in $Q_1$ its source and target in $Q_0$ .

A quiver Q is connected if its underlying undirected graph is connected. A quiver is acyclic if it does not contain any directed cycles. By a subquiver S of Q, we mean a quiver $S = (S_0,S_1)$ such that $S_i \subseteq Q_i$ for $i = 0,1$ .

Example 2.4. For a nonnegative integer n, we let ${\mathbb {L}}_n$ be the quiver with one vertex and n loops. ${\mathbb {L}}_1$ is called the Jordan quiver.

Throughout this paper, we will simply denote a quiver by Q and the underlying undirected graph of a quiver Q by $\overline {Q}$ . We will also use the basic terminology of undirected graphs to Q; when we say some graph-theoretic property holds for Q, it means that it holds for $\overline {Q}$ . For example, when we say Q is a tree, it means that $\overline {Q}$ is a tree.

Definition 2.5. Let S and Q be quivers.

1. 1. A quiver map $F : S \rightarrow Q$ consists of a pair of functions

   $$ \begin{align*} F_i : S_i \rightarrow Q_i, \quad i=0,1, \end{align*} $$
   which satisfy the following conditions: for all $\alpha \in S_1$ ,
   $$ \begin{align*} s(F_1(\alpha)) = F_0(s(\alpha)), \quad t(F_1(\alpha)) = F_0(t(\alpha)). \end{align*} $$

2. 2. A quiver map F is said to be injective (resp. surjective) if and only if $F_0$ and $F_1$ are both injective (resp. surjective).

With the notion of quiver maps, we can identify a subquiver S of Q with the image of the inclusion map $S \hookrightarrow Q$ . A subquiver S is said to be full if for any $u, v \in S_0$ , any arrow $\alpha $ in $Q_1$ such that $u=s(\alpha )$ and $v=t(\alpha )$ (or $u=t(\alpha )$ and $v=s(\alpha )$ ) is also in $S_1$ .

Definition 2.6. Let Q be a quiver with underlying graph $G =\overline {Q}$ . Recall that a walk in G is a sequence of edges $ w = (e_1, \ldots , e_d)$ such that $e_i$ and $e_{i+1}$ share an endpoint. In other words, it is a sequence of vertices $(v_1,v_2,\ldots , v_d, v_{d+1})$ together with a specification of an edge $e_i$ between $v_i$ and $v_{i+1}$ for all $i\le d$ . Let $\alpha _i$ be the arrow in Q corresponding to the edge $e_i$ of G. Define $\epsilon _i = +1$ if $s(\alpha _i) = v_i$ and $t(\alpha _i) = v_{i+1}$ , and $\epsilon _i = -1$ if $s(\alpha _i) = v_{i+1}$ and $t(\alpha _i) = v_i$ . Then we will write a walk of Q as follows:

$$ \begin{align*} w = \alpha_1^{\epsilon_1}\cdots \alpha_d^{\epsilon_d}. \end{align*} $$

A path is a directed walk in the sense that all $\epsilon _i$ have the same sign.

Definition 2.7. Let Q be a quiver with underlying graph $\overline {Q}$ . Then $\overline {Q}$ is a $1$ -simplex, whose $0$ -simplices can be identified with $Q_0$ and whose $1$ -simplices can be identified with  $Q_1$ . We then obtain a chain complex

$$ \begin{align*} 0 \rightarrow \mathbb{Z}Q_1 \xrightarrow[]{\partial} \mathbb{Z}Q_0 \rightarrow 0, \end{align*} $$

where $\mathbb {Z}Q_1$ and $\mathbb {Z}Q_0$ denote the free abelian groups generated by arrows and vertices, respectively, with $\partial $ defined via the formula $\partial (\alpha ) = t(\alpha ) - s(\alpha )$ , for $\alpha \in Q_1$ . The (integral) cycle space is defined to be the first homology group $H_1(Q, \mathbb {Z}) = \operatorname {ker}(\partial )$ . Note that the cycle space is a finitely generated free abelian group, and a basis for $H_1(Q,\mathbb {Z})$ is called a (integral) cycle basis for Q. Note that the cycle space does not depend on the choice of orientation of $\overline {Q}$ : indeed, the orientation functions simply as a device for writing elements of $\operatorname {ker}(\partial )$ as $\mathbb {Z}$ -linear combinations of $1$ -simplices.

Example 2.8. Consider the following quiver:

Then, we obtain the following chain complex:

$$ \begin{align*} 0 \rightarrow \mathbb{Z}^4 \xrightarrow[]{\partial} \mathbb{Z}^4 \rightarrow 0, \end{align*} $$

where $\partial $ is given by the following matrix:

Then, $\ker (\partial )$ is generated by , or $(\alpha _1-\alpha _2-\alpha _3+\alpha _4)$ corresponding to the unique cycle of Q.

Definition 2.9. Let Q be a connected quiver. We say that Q is a pseudotree if $\operatorname {rank}(H_1(Q,\mathbb {Z})) \le 1$ . If Q is not a tree or an affine Dynkin quiver of type $\tilde {\mathbb {A}}_n$ , we say that Q is a proper pseudotree. Any proper pseudotree contains a unique subquiver C that is an affine Dynkin quiver of type $\tilde {\mathbb {A}}_n$ : we call C the central cycle of Q.

Definition 2.10. [27, Def. 4.1]

Let Q be a quiver.

1. 1. A representation of Q over ${\mathbb {F}}_1$ (or an ${\mathbb {F}}_1$ -representation of Q) is the collection of data $\mathbb {V}=(V_i,f_\alpha )$ consisting of an ${\mathbb {F}}_1$ -vector space $V_i$ for each vertex $i \in Q_0$ and an ${\mathbb {F}}_1$ -linear map $f_\alpha \in {\operatorname {Hom}}(V_{s(\alpha )},V_{t(\alpha )})$ for each arrow $\alpha \in Q_1$ .

2. 2. By a subrepresentation $\mathbb {W}=(W_i,g_\alpha )$ of $\mathbb {V}=(V_i,f_\alpha )$ , we mean an ${\mathbb {F}}_1$ -representation such that each $W_i$ is a subspace of $V_i$ and $g_\alpha $ is a restriction of $f_\alpha $ . When $\mathbb {W}$ is a subrepresentation of $\mathbb {V}$ , we write $\mathbb {W} \leq \mathbb {V}$ .

Definition 2.11 [27, Def. 4.3]

Let Q be a quiver, and let $\mathbb {V}=(V_i,f_\alpha )$ be an ${\mathbb {F}}_1$ -representation of Q.

1. 1. The dimension of $\mathbb {V}$ is defined to be the sum of dimensions of $V_i$ :

   $$ \begin{align*} \dim(\mathbb{V})=\sum_{i \in Q_0} \dim_{{\mathbb{F}}_1}(V_i). \end{align*} $$

2. 2. The dimension vector of $\mathbb {V}$ is an element of $\mathbb {N}^{|Q_0|}$ :

   $$ \begin{align*} \mathbf{{dim}}(\mathbb{V})=(\dim_{{\mathbb{F}}_1}(V_i))_{i \in Q_0}. \end{align*} $$

An ${\mathbb {F}}_1$ -representation $\mathbb {V}=(V_i,f_\alpha )$ is nilpotent if there exists a positive integer N such that $\forall ~n \geq N$ and any path $\alpha _1\alpha _2\dots \alpha _n$ in Q (left-to-right in the order of traversal), one has

$$ \begin{align*} f_{\alpha_n}f_{\alpha_{n-1}}\cdots f_{\alpha_1}=0\ \mathrm{(zero map). } \end{align*} $$

Definition 2.12. Let $\mathbb {V}=(V_i,f_\alpha )$ and $\mathbb {W}=(W_i,g_\alpha )$ be ${\mathbb {F}}_1$ -representations of a quiver Q. A morphism $\Phi :\mathbb {V} \to \mathbb {W}$ is a collection of ${\mathbb {F}}_1$ -linear maps $\{\phi _i:V_i\to W_i\}_{i \in Q_0}$ making the following diagram commute:

(2.1)

We denote by $\mathrm {Rep}(Q,\mathbb {F}_1)$ the category whose objects are ${\mathbb {F}}_1$ -representations of Q and whose morphisms are defined as above. We let $\mathrm {Rep}(Q,\mathbb {F}_1)_{\mathrm {nil}}$ be the full subcategory of $\mathrm {Rep}(Q,\mathbb {F}_1)$ consisting of nilpotent representations.

We note that each morphism $\Phi \in {\operatorname {Hom}}(\mathbb {V},\mathbb {W})$ has a kernel and cokernel obtained from a kernel and cokernel at each vertex. Similarly, one obtains the notions of subrepresentations and quotient representations. We refer the reader to [27, Def. 4.3] for details.

Remark 2.13. Recall that an ${\mathbb {F}}_1$ -representation $\mathbb {V}$ of a quiver Q is indecomposable if $\mathbb {V}$ cannot be written as a nontrivial direct sum of subrepresentations. In [27], Szczesny proves that the Krull–Schmidt theorem holds for the category ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ . To be precise, any ${\mathbb {F}}_1$ -representation M can be written uniquely (up to permutation) as a finite direct sum of indecomposable representations.

Let k be a field and ${\operatorname {Vect}}(k)$ be the category of finite-dimensional vector spaces over k. Then, one may define “the base change functor” as follows: ⁸

(2.2) $$ \begin{align} k\otimes_{{\mathbb{F}}_1} -:\mathrm{Vect}(\mathbb{F}_1) \to \mathrm{Vect}(k), \end{align} $$

where any ${\mathbb {F}}_1$ -vector space V goes to the vector space whose basis is $V-\{0_V\}$ .

Note that representations of a quiver can be defined in a more categorical way. Let Q be a quiver. One can consider a discrete category $\mathcal {Q}$ : objects are vertices of Q and morphisms are directed paths. Then, a representation M of Q over ${\mathbb {F}}_1$ is nothing but a functor $\mathbf {M}: \mathcal {Q} \to \mathrm {Vect}(\mathbb {F}_1)$ . In particular, $\mathrm {Rep}(Q,{\mathbb {F}}_1)$ is equivalent to the functor category $\mathrm {Vect}(\mathbb {F}_1)^{\mathcal {Q}}$ . In fact, the same description holds for representations of Q over a field k. Therefore, from the base-change functor $k\otimes _{{\mathbb {F}}_1} -$ , one has the following base-change functor, which is faithful (but not full in general):

(2.3) $$ \begin{align} k\otimes_{{\mathbb{F}}_1} -:\mathrm{Rep}(Q,{\mathbb{F}}_1) \to \mathrm{Rep}(Q,k), \quad M \to M_k. \end{align} $$

The base-change functor will be considered in §5 to compute Euler characteristic of quiver Grassmannians associated with a class of quiver representations.

2.2 Hall algebras for $\mathrm {Rep}(Q,{\mathbb {F}}_1)$

There are two (equivalent) ways to construct the Hall algebra $H_Q$ of $\mathrm {Rep}(Q,{\mathbb {F}}_1)$ . The first way is to appeal to some categorical interpretation of ${\mathbb {F}}_1$ -representations of Q. As we mentioned above, $\mathrm {Rep}(Q,{\mathbb {F}}_1)$ is equivalent to the functor category $\mathrm {Vect}(\mathbb {F}_1)^{\mathcal {Q}}$ . Since ${\operatorname {Vect}}({\mathbb {F}}_1)$ is proto-exact in the sense of Dyckerhoff and Kapranov [5], where they also prove that for a small category $\mathcal {I}$ , the functor category $\mathcal {C}^{\mathcal {I}}$ is proto-exact for a proto-exact category $\mathcal {C}$ . The construction of $H_Q$ then follows from a more general construction of Hall algebras in [5].

The second construction is to mimic the classical construction of the Hall algebra of representations of Q over ${\mathbb {F}}_q$ . To be precise, let $\mathrm {Iso}(Q)$ be the set of isomorphism classes of objects in $\mathrm {Rep}(Q,\mathbb {F}_1)$ . The Hall algebra $H_Q$ of $\mathrm {Rep}(Q,\mathbb {F}_1)$ has the following underlying set:

(2.4) $$ \begin{align} H_Q:=\{f:\mathrm{Iso}(Q) \to \mathbb{C} \mid f([M])=0\textrm{ for all but finitely many }[M].\}. \end{align} $$

For each $[M] \in \mathrm {Iso}(Q)$ , let $\delta _{[M]}$ be the delta function in $H_Q$ supported at $[M]$ . In particular, we consider $H_Q$ as the vector space spanned by $\{\delta _{[M]}\}_{[M] \in \mathrm {Iso}(Q)}$ over $\mathbb {C}$ . To ease the notation, we will denote the delta function $\delta _{[M]}$ by $[M]$ . One defines the following multiplication on the elements in $\mathrm {Iso}(Q)$ :

(2.5) $$ \begin{align} [M]\cdot[N]:=\sum_{R \in \mathrm{Iso}(Q)} \frac{a^R_{M,N}}{a_Ma_N}[R], \end{align} $$

where $a_M=|\mathrm {Aut}(M)|$ and $a^R_{M,N}$ is the number of “short exact sequences” of the form: ⁹

$$ \begin{align*} 0 \to N \to R \to M \to 0. \end{align*} $$

Then, one can easily check the following equality as in the classical case:

$$ \begin{align*} \frac{a^R_{M,N}}{a_Ma_N}=|\{L \leq R \mid L\simeq N\ \mathrm{and}\ R/L \simeq M\}|. \end{align*} $$

By linearly extending the multiplication (2.5) to $H_Q$ , we obtain an associative algebra $H_Q$ over $\mathbb {C}$ . Moreover, one may check that $H_Q$ is also equipped with the coproduct defined as follows:

(2.6) $$ \begin{align} \Delta:H_Q\to H_Q\otimes_{\mathbb{C}}H_Q, \quad \Delta(f)([M],[N])=f([M\oplus N]). \end{align} $$

With (2.5) and (2.6), Szczesny proves various interesting results. We refer the interested reader to [27, §6] for details.

2.3 Coefficient quivers

Coefficient quivers ¹⁰ were first introduced by Ringel [24] as a combinatorial gadget to study representations of quivers.

Let $\mathbb {V}=(V_i,f_\alpha )$ be a representation of a quiver Q over $\mathbb {C}$ . We fix a basis $B(i)$ for each vector space i and let $B=\bigsqcup _{i \in Q_0}B(i)$ , that is, B is a basis for the vector space $\bigoplus _{i \in Q_0}V_i$ . We simply call B a basis for $\mathbb {V}$ .

Definition 2.14. The coefficient quiver $\tilde {Q}=\tilde {Q}(\mathbb {V},B)$ is a quiver defined as follows:

1. 1. $\tilde {Q}_0=B$ .

2. 2. For every arrow $\alpha :v \to w$ of Q and every element $x \in B(v)$ , if we can write

   $$ \begin{align*} f_\alpha(x)=\sum c_b b, \quad b \in B(w), c_b\neq 0, \end{align*} $$
   then we draw an arrow from x to $b \in B(w)$ in $\tilde {Q}$ , and label it with $\alpha $ .

The coefficient quiver depends on a choice of a basis for a representation $\mathbb {V}$ of Q.

Example 2.15.

Consider the following representation $\mathbb {V}$ of Q:

$$ \begin{align*} V_1=\mathbb{C}^2, \quad V_2=\mathbb{C}, \quad V_3=\mathbb{C}^2. \end{align*} $$

$$ \begin{align*} f_\alpha=\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, \quad f_\beta=\begin{bmatrix} 0 \\ 1 \end{bmatrix}, \quad f_\gamma=\begin{bmatrix} 0 & -1 \\ 0 & 0 \end{bmatrix}. \end{align*} $$

Let us fix bases: $B_1=\{e_1,e_2\}$ , $B_2=\{1\}$ , and $B_3=\{e_1+e_2,e_2\}$ . Then, we obtain the following coefficient quiver.

Let us change bases: $B_1'=\{e_1-e_2,e_2\}$ , $B_2'={1}$ , and $B_3'=\{e_1,e_2\}$ . Then, we have the following coefficient quiver:

3 The slice category over Q and $\mathrm {Rep}(Q,{\mathbb {F}}_1)$

A notion of windings of quivers was first introduced by Crawley-Boevey [4] and Krause [15] to define morphisms between tree and band modules. Later, Haupt [7, §2.3] generalized Krause’s definition of windings as follows. ¹¹ Let Q and S be quivers. A winding of quivers $F:S\to Q$ is a morphisms of quivers

$$ \begin{align*} F_0:S_0 \to Q_0, \quad F_1:S_1 \to Q_1, \end{align*} $$

satisfying the following two conditions:

1. 1. If $\alpha ,\beta \in S_1$ with $\alpha \neq \beta $ and $s(\alpha )=s(\beta )$ , then $F_1(\alpha ) \neq F_1(\beta )$ .

2. 2. If $\alpha ,\beta \in S_1$ with $\alpha \neq \beta $ and $t(\alpha )=t(\beta )$ , then $F_1(\alpha ) \neq F_1(\beta )$ .

For a winding map $F:S \to Q$ , it is easy to check that for an S-representation V over a field k, the pushforward $F_*(V)$ is a Q-representation over k. ¹² In particular, is said to be a tree module if S is a tree, where is the representation of S assigning k to each vertex and the identity map to each arrow. The following lemma shows that the same is true for $\mathbb {F}_1$ -representations.

Lemma 3.1. Let $F:S \to Q$ be a winding map of quivers. For each $v \in Q_0$ , let $M_v=F^{-1}(v) \cup \{0\}$ . For each $\alpha \in Q_1$ , consider the following function: let $v=s(\alpha )$ , $w=t(\alpha )$ ,

(3.1) $$ \begin{align} \tilde{\alpha}: M_v \to M_w, \quad x \mapsto \begin{cases} y,\ \mathrm{if}\ \ \exists \beta \in S_1\ \mathrm{such\ that}\ s(\beta)=x,~t(\beta)=y,~F(\beta)=\alpha,\\ 0,\ \mathrm{otherwise.} \end{cases} \end{align} $$

Then, $(M_v,\tilde {\alpha })_{v \in Q_0, \alpha \in Q_1}$ is an $\mathbb {F}_1$ -representation of Q. By abuse of notation, we denote this $\mathbb {F}_1$ -representation of Q by $F_*(S)$ .

Proof We only have to check that $\tilde {\alpha }$ is a well-defined $\mathbb {F}_1$ -linear map. In fact, suppose that we have $\beta ,\beta ' \in S_1$ and $x \in M_v$ such that $s(\beta )=s(\beta ')=x$ and $F(\beta )=F(\beta ')=\alpha \in Q_1$ . Since F is a winding map, this implies that $\beta =\beta '$ , and hence $\tilde {\alpha }$ is well defined.

Next, suppose that $\tilde {\alpha }(x)=\tilde {\alpha }(z) = e\neq 0$ . In other words, there exist $\beta _x, \beta _z \in S_1$ such that

$$ \begin{align*} s(\beta_x)=x, \quad s(\beta_z)=z, \quad t(\beta_x)=e=t(\beta_z), \quad F(\beta_x)=F(\beta_z)=\alpha. \end{align*} $$

But, again since F is a winding map, this implies that $\beta _x=\beta _z$ , showing that $x=z$ . Hence, $\tilde {\alpha }$ is an $\mathbb {F}_1$ -linear map.

Lemma 3.2. Let Q be a quiver, and let $\mathbb {V}=(M_v,f_\alpha )$ be an ${\mathbb {F}}_1$ -representation of Q. Then, there exists a winding map of quivers $F:S\to Q$ such that $F_*(S) \simeq \mathbb {V}$ .

Proof This construction is essentially the same as the one given in [10], but we include it here for completeness. We first define the set of vertices of a quiver S as follows:

$$ \begin{align*} S_0:= \bigsqcup_{v \in Q_0}M_v\setminus \{0\}. \end{align*} $$

For each $x, y \in S_0$ , we draw an arrow $\beta _\alpha :x \to y$ in $S_1$ if and only if $x \in M_v$ , $y \in M_w$ and there exist $\alpha \in Q_1$ and $f_\alpha $ such that $s(\alpha )=v$ , $t(\alpha )=w$ , and $f_\alpha (x)=y$ . Note that if there is another $\alpha ' \in Q_1$ with the same property, then we draw two different arrows $\beta _\alpha $ and $\beta _{\alpha '}$ .

Next, we define a winding map $F:S \to Q$ as follows: for each $x_v \in S_0$ , $x_v \in M_v \setminus \{0\}$ for some $v \in Q_0$ , we let $F(x_v)=v$ . We send each arrow $\beta _{\alpha }\in S_1$ to $\alpha $ . One can easily check that F is a quiver map. To check the winding condition, suppose $\beta _{\alpha } \neq \beta _{\alpha '} \in S_1$ and $s(\beta _{\alpha })=s(\beta _{\alpha '})$ . If $t(\beta _{\alpha }) = t(\beta _{\alpha '})$ , then $\beta _{\alpha } \neq \beta _{\alpha '}$ implies $F(\beta _{\alpha }) =\alpha \neq \alpha ' = F(\beta _{\alpha '})$ , since there is at most one $\alpha $ -labeled arrow between any two vertices of S. Now, suppose that $t(\beta _{\alpha }) \neq t(\beta _{\alpha '})$ . Since $t(\beta _{\alpha }) = f_{\alpha }(s(\beta _{\alpha }))$ and $t(\beta _{\alpha '}) = f_{\alpha '}(s(\beta _{\alpha '}))$ , we must have $\alpha \neq \alpha '$ , which implies $F(\beta _{\alpha }) \neq F(\beta _{\alpha '})$ again. Hence, the first condition for F to be a winding has been verified. The second condition is similar.

To define the category of quivers over a quiver, we first recall some definitions. Let T be a full subquiver of S. We say that the $T_0$ is predecessor-closed if the following condition holds: for any oriented path in S from v to w if $w \in T_0$ , then $v \in T_0$ . Analogously $T_0$ is successor-closed if the following condition holds: for any oriented path in S from v to w, if $v \in T_0$ , then $w \in T_0$ .

Remark 3.3. We caution the reader that the authors use the opposite convention for successor- and predecessor-closed subsets in [10].

Let Q be a fixed quiver. Let $\mathcal {C}_Q$ be the category whose objects are windings of quivers $F:S \to Q$ . A morphism $\phi : (S,F)\rightarrow (S',F')$ is an ordered triple $\phi = (\mathcal {U}_{\phi }, \mathcal {D}_{\phi }, c_{\phi })$ , where:

1. 1. $\mathcal {U}_{\phi }$ is a full subquiver of S whose vertex set is predecessor-closed,

2. 2. $\mathcal {D}_{\phi }$ is a full subquiver of $S'$ whose vertex set is successor-closed, and

3. 3. $c_{\phi } : \mathcal {U}_{\phi } \rightarrow \mathcal {D}_{\phi }$ is a quiver isomorphism such that the diagram below commutes.

(3.2)

If $(S,F) \xrightarrow []{\phi } (S',F')$ and $(S',F') \xrightarrow []{\psi } (S", F")$ are two morphisms in $\mathcal {C}_Q$ , their composition $(S,F)\xrightarrow []{\psi \circ \phi } (S", F")$ is the ordered triple

(3.3) $$ \begin{align} \psi \circ \phi = \left( \mathcal{U}_{\psi\circ \phi}, \mathcal{D}_{\psi \circ \phi}, c_{\psi\circ\phi} \right) = \left( c_{\phi}^{-1}\left( \mathcal{U}_{\psi} \cap \mathcal{D}_{\phi} \right), c_{\psi}\left( \mathcal{U}_{\psi}\cap \mathcal{D}_{\phi} \right), c_{\psi} \circ c_{\phi} \right). \end{align} $$

Of course, the composition $c_{\psi }\circ c_{\phi }$ is understood to be restricted to $c_{\phi }^{-1}\left ( \mathcal {U}_{\psi } \cap \mathcal {D}_{\phi } \right )$ . Loosely, one can think of composition as gluing the top of S to the bottom of $S'$ in a way that respects the mappings F and $F'$ . One can check $\mathcal {C}_Q$ indeed satisfies the axioms of a category.

Let $\phi :(S,F) \to (S',F')$ be a morphism in $\mathcal {C}_Q$ . Then, $\phi $ induces a morphism $\phi _*:F_*(S) \to F^{\prime }_*(S')$ of ${\mathbb {F}}_1$ -representations of Q as follows: for each $v \in Q_0$ , we define the map

(3.4) $$ \begin{align} (\phi_*)_v:F_*(S)_v\to F^{\prime}_*(S')_v \end{align} $$

as

(3.5) $$ \begin{align} (\phi_*)_v(x) = \begin{cases} c_\phi(x), \textrm{ if }x \in \mathcal{U}_\phi \cap F_*(S)_v,\\ 0, \textrm{ otherwise.} \end{cases} \end{align} $$

Since $c_\phi $ is an isomorphism, clearly $(\phi _*)_v$ is an ${\mathbb {F}}_1$ -linear map. Next, let $\alpha \in Q_1$ with $v=s(\alpha )$ and $w=t(\alpha )$ . Suppose first that $x \not \in \mathcal {U}_\phi \cap F_*(S)_v$ , in particular, $(\phi _*)_v(x)=0$ . Since $x \not \in \mathcal {U}_\phi $ and $\mathcal {U}_\phi $ is predecessor-closed, we have that $\tilde {\alpha }(x) \not \in \mathcal {U}_\phi $ , where $\tilde {\alpha }$ is a map defined in (3.1). Hence, in this case, we have

(3.6) $$ \begin{align} \tilde{\alpha}(\phi_*)_v(x) = (\phi_*)_w\tilde{\alpha}(x). \end{align} $$

Now, suppose that $x \in \mathcal {U}_\phi \cap F_*(S)_v$ and $y=c_\phi (x)$ . If $\tilde {\alpha }(y)=0$ , then $\tilde {\alpha }(x)\not \in \mathcal {U}_{\phi }$ , since $c_{\phi }$ is an isomorphism. In particular, $(\phi _*)_w\tilde {\alpha }(x) = 0$ , and we have (3.6) in this case. Finally, if $\tilde {\alpha }(y)=z$ , then $z \in \mathcal {D}_\phi $ since $y \in \mathcal {D}_\phi $ and it is successor-closed. In particular, there exists an arrow $\beta $ in $\mathcal {D}_\phi $ such that $s(\beta )=y$ and $t(\beta )=z$ . Since $c_\phi $ is an isomorphism, this implies that $\tilde {\alpha }(x) \in \mathcal {U}_\phi $ and $(\phi _*)_w\tilde {\alpha }(x)=z$ , showing that (3.6) is valid in this case as well. Therefore, the following diagram commutes and $\phi _*$ is indeed a morphism of ${\mathbb {F}}_1$ -representations.

(3.7)

Remark 3.4. Before we proceed to prove an equivalence between $\mathcal {C}_Q$ and ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ , we remark the following.

1. 1. Our definition for morphisms in $\mathcal {C}_Q$ generalizes the notion of maps between tree modules in [4, §2]. We also note that the notion of admissible triple in [15] is similar to our definition in the sense that to define a morphism $\phi :(S,F) \to (S',F')$ , we first assume an isomorphism of a subquiver of S and a subquiver of $S'$ satisfying certain conditions, whereas in [15], this is done by using “connecting triple” rather than directly identifying subquivers. For details, see [15, pp. 189–191].

2. 2. The notion of tree modules in [4, 15] is more restrictive than the notion of tree modules given in [24] due to the “winding” conditions imposed on quiver maps.

Lemma 3.5. For an object $F:S\to Q$ in $\mathcal {C}_Q$ , we let $\mathbf {F}(S)$ be the $\mathbb {F}_1$ -representation of Q as in Lemma 3.1. For a morphism $\phi :(S,F) \to (S',F)$ , we let $\mathbf {F}(\phi )$ be the morphism between $\mathbf {F}(S)$ and, $\mathbf {F}(S')$ which we described above. Then, $\mathbf {F}:\mathcal {C}_Q \to \text {Rep}(Q,{\mathbb {F}}_1)$ defines a functor.

Proof One can easily check that an identity map $\phi :(S,F) \to (S,F)$ in $\mathcal {C}_Q$ maps to the identity map in $\mathrm {Rep}(Q,{\mathbb {F}}_1)$ since in this case $\mathcal {U}_\phi =\mathcal {D}_\phi =S$ and $c_\phi $ is the identity map.

Next, suppose that $\phi :(S,F) \to (S',F')$ and $\psi : (S',F') \to (S", F")$ are two morphisms in $\mathcal {C}_Q$ . We want to check that $\mathbf {F}(\psi \phi )=\mathbf {F}(\psi )\mathbf {F}(\phi )$ . With the same notation as in (3.4) and (3.5), we only have to show that

(3.8) $$ \begin{align} ((\psi\phi)_*)_v=((\psi)_*)_v((\phi)_*)_v. \end{align} $$

But, this is clear from (3.3).

Lemma 3.6. Let $S=(S,F),S'=(S',F')$ be objects in $\mathcal {C}_Q$ , $\phi :F_*(S) \to F^{\prime }_*(S')$ a morphism in $\text {Rep}(Q,{\mathbb {F}}_1)$ , and $\mathcal {U}_\phi $ the full subquiver of S with the vertex set $S_0\setminus \ker (\phi )$ . Then, $\phi $ induces a quiver map $f:\mathcal {U}_\phi \to S'$ such that $f(\mathcal {U}_\phi )$ is successor-closed.

Proof This follows from Construction 3.9 and the proof of Lemma 3.10 in [10].

Proposition 3.7. The functor $\mathbf {F}:\mathcal {C}_Q \to \text {Rep}(Q,{\mathbb {F}}_1)$ is an equivalence of categories. This restricts to an equivalence between ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}$ and the full subcategory of $\mathcal {C}_Q$ whose objects are windings $F:S \to Q$ with S acyclic.

Proof Lemmas 3.2 and 3.5 show that $\mathbf {F}$ is an essentially surjective functor, and hence we only have to prove that $\mathbf {F}$ is fully faithful. But this is just Lemma 3.10 of [10]. ¹³

In what follows, we often denote the winding corresponding to an ${\mathbb {F}}_1$ -representation M of a quiver Q by $c:\Gamma _M \to Q$ . We will simply call $\Gamma _M$ the coefficient quiver of M.

The following example is taken from [7] and is restated in terms of $\mathbb {F}_1$ -representation.

Example 3.8 ([7, Exam. 2.5])

Let $F:S \to Q$ be an object in $\mathcal {C}_Q$ described in the following picture:

Then, is the following representation of S over a field k:

Note that by definition, is a tree module, given as follows:

where

$$ \begin{align*} A=\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \quad B=\begin{bmatrix} 0 \\ 1\\ 0 \end{bmatrix}, \quad C=\begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix}, \end{align*} $$

Now, we view S as the coefficient quiver of an ${\mathbb {F}}_1$ -representation. The ${\mathbb {F}}_1$ -representation $\mathbb {V}=F_*(S)$ of Q is the following: at each vertex of Q, we have

$$ \begin{align*} M_{v_1}=\{0, v_1\}, \quad M_{v_2}=\{0, v_2\},\quad M_{v_3}=\{0,v_3,v_{3'},v_{3"}\}. \end{align*} $$

${\mathbb {F}}_1$ -linear maps between vertices are given as follows:

$$ \begin{align*} \tilde{\alpha}:M_{v_1} \to M_{v_3}, \quad v_1 \mapsto v_{3'}, \end{align*} $$

$$ \begin{align*} \tilde{\beta}:M_{v_2} \to M_{v_3}, \quad v_2 \mapsto v_{3'}, \end{align*} $$

$$ \begin{align*} \tilde{\gamma}: M_{v_3} \to M_{v_3}, \quad v_3 \mapsto v_{3'}, \quad v_{3'} \mapsto v_{3"}, \quad v_{3"} \mapsto 0. \end{align*} $$

One can easily see that .

Now, we depict the corresponding coefficient quiver $\Gamma _{\mathbb {V}}$ for $\mathbb {V}$ . First, we consider the following coloring:

We let $\alpha $ in green, $\beta $ in purple, and $\gamma $ in black. Then, the coefficient quiver $\Gamma _{\mathbb {V}}$ is as follows:

Remark 3.9. Let $f:S \to Q$ be a quiver map (without winding condition), and let k be a field. The map f induces a functor (pushforward)

(3.9) $$ \begin{align} f_*:{\operatorname{Rep}}(S,k) \to {\operatorname{Rep}}(Q,k) \end{align} $$

which we briefly recall here. We refer the reader to [13], [14] for more details. For a representation V of S over k, the pushforward $f_*(V)$ is defined as follows:

(3.10) $$ \begin{align} f_*(V)v:=\bigoplus_{w \in f^{{-1}}(v)} V_w, \quad v \in Q_0, \qquad f_*(V)_\alpha=\sum_{\beta \in f^{-1}(\alpha)} V_\beta, \quad \beta \in Q_1. \end{align} $$

Recall that by the identity representation of S, we mean a representation of S over k consisting of one-dimensional vector space at each vertex and identity map at each arrow. In particular, each quiver map $f:S \to Q$ defines a representation of Q, namely .

Let $\mathcal {D}_Q$ be the category whose objects are quiver maps $f:Q' \to Q$ (without winding condition) and morphisms are the same as $\mathcal {C}_Q$ . Then, we have a faithful inclusion functor $i:\mathcal {C}_Q \to \mathcal {D}_Q$ .

For each $f:S \to Q$ in $\mathcal {D}_Q$ , we let . For a morphism $\phi :S \to S'$ in $\mathcal {D}_Q$ , where S (resp. $S'$ ) means $f:S \to Q$ (resp. $f':S' \to Q$ ). In fact, the same definition as in (3.4) and (3.5) can be used to define a functor:

From the definition, one can easily check that the functor is faithful. To summarize, we have the following commutative diagram of categories.

(3.11)

Definition 3.10. Let Q be a quiver. An ${\mathbb {F}}_1$ -representation M is called a tree module if $\Gamma _M$ is a tree. This is equivalent to with $f : S\rightarrow Q$ a winding and S a tree. M will be called an ${\mathbb {F}}_1$ -band module if the coefficient quiver of M is an affine Dynkin quiver of type $\tilde {\mathbb {A}}$ .

Remark 3.11. Let M be an ${\mathbb {F}}_1$ -band. Then, $\Gamma _M$ is connected, so M is always indecomposable as an ${\mathbb {F}}_1$ -representation. However, since we do not require that the associated winding map $c_M : \Gamma _M \rightarrow Q$ is primitive (see Definition 5.19), $M\otimes _{{\mathbb {F}}_1}k$ may be decomposable. If M is an ${\mathbb {F}}_1$ -band module and $c_M$ is primitive, then $M\otimes _{{\mathbb {F}}_1}k$ is a band module in the usual sense, but the converse does not generally hold.

4 Gradings on representations

In [1], Cerulli Irelli proved that when a quiver representation over $\mathbb {C}$ satisfies certain conditions, ¹⁴ then one can compute the Euler characteristics of quiver Grassmannians for some special classes of quivers in a purely combinatorial way. Later, in [7], Haupt generalized Cerulli Irelli’s results by introducing the notion of a grading on a representation of Q. The following appear as Definitions 4.1 and 4.2 of [7].

Definition 4.1 (Haupt)

Let M be an ${\mathbb {F}}_1$ -representation of Q, and let $(\Gamma ,c) := (\Gamma _M,c_M)$ denote the associated coefficient quiver. By a grading of M, we mean a map $\partial : \Gamma _0 \rightarrow {\mathbb {Z}}$ . Suppose that $\partial _1,\ldots , \partial _n$ and $\partial $ are gradings for M. Suppose further that for any two arrows $\beta , \beta ' \in \Gamma _1$ , the equalities

(4.1) $$ \begin{align} \partial_i(s(\beta)) = \partial_i(s(\beta')),i = 1,\ldots , n, \end{align} $$

(4.2) $$ \begin{align} \partial_i(t(\beta)) = \partial_i(t(\beta')), i = 1,\ldots, n, \end{align} $$

(4.3) $$ \begin{align} c(\beta) = c(\beta') \end{align} $$

imply

(4.4) $$ \begin{align} \partial(t(\beta)) - \partial(s(\beta)) = \partial(t(\beta')) - \partial(s(\beta')). \end{align} $$

Then, we say that $\partial $ is a nice $(\partial _1,\ldots ,\partial _n)$ -grading. A nice  $\emptyset $ -grading (or nice grading for short) is a grading such that $c(\beta ) = c(\beta ')$ implies (4.4).

Remark 4.2. Haupt’s original definition applies to representations over fields, where it is necessary to first specify a basis for M. Since representations over $\mathbb {F}_1$ have a unique basis, the definition above is unambiguous. In other words, a nice grading for an $\mathbb {F}_1$ -representation M is the same thing as a nice grading for $M_{\mathbb {C}}$ with respect to the basis $M\setminus \{0\}$ , and so on.

Remark 4.3. An ${\mathbb {F}}_1$ -representation M is completely determined by its associated winding map $c_M$ . Hence, we will use the terms “nice grading for M” and “nice grading for $c_M : \Gamma _M \rightarrow Q$ ” interchangeably. From Proposition 3.7, if $c : \Gamma \rightarrow Q$ is a winding, then there is a unique (up to isomorphism) ${\mathbb {F}}_1$ -representation of Q, call it M, such that $(c_M, \Gamma _M) = (c,\Gamma )$ . Hence, we can also discuss a nice grading for a general winding, without explicit reference to its associated representation.

Definition 4.4. Let $F : S \rightarrow Q$ be a winding, and let $\partial : S_0 \rightarrow {\mathbb {Z}}$ be a nice grading. If $\beta \in S_1$ with $F(\beta ) = \alpha $ , define $\Delta _{\alpha }^{\partial } = \partial (t(\beta )) - \partial (s(\beta ))$ . ¹⁵ If $\partial $ is understood from context, we will abbreviate $\Delta _{\alpha }^{\partial } = \Delta _{\alpha }$ . We say that $\partial $ is:

1. 1. nontrivial if $\Delta _{\alpha } \neq 0$ for some $\alpha \in Q_1$ ,

2. 2. non-degenerate if $\Delta _{\alpha } \neq 0$ for all $\alpha \in Q_1$ , and

3. 3. positive (resp. negative) if $\Delta _{\alpha }> 0$ (resp. $\Delta _{\alpha } < 0$ ) for all $\alpha \in Q_1$ .

More generally, suppose that $\partial $ is a $(\partial _1,\ldots , \partial _n)$ -nice grading. If $\beta \in S_1$ with

(4.5) $$ \begin{align} F_1(\beta) = \alpha, \end{align} $$

(4.6) $$ \begin{align} (\partial_1(s(\beta)),\ldots , \partial_n(s(\beta))) = \mathbf{s} \in \mathbb{Z}^n, \end{align} $$

(4.7) $$ \begin{align} (\partial_1(t(\beta)),\ldots , \partial_n(t(\beta))) = \mathbf{t} \in \mathbb{Z}^n, \end{align} $$

then we define

(4.8) $$ \begin{align} \Delta_{\alpha,\mathbf{s},\mathbf{t}}^{\partial} := \partial(t(\beta)) - \partial(s(\beta)). \end{align} $$

As before, when $\partial $ is understood, we abbreviate $\Delta _{\alpha ,\mathbf {s},\mathbf {t}}^{\partial } = \Delta _{\alpha ,\mathbf {s},\mathbf {t}}$ . The notions of nontrivial/non-degenerate/positive/negative $(\partial _1,\ldots ,\partial _n)$ -nice gradings are defined in the obvious manner.

As in [7], we will be interested in building sequences of nice gradings which have certain desirable properties. The definition below helps us formalize this process.

Definition 4.5. Let $c : \Gamma \rightarrow Q$ be a winding. A nice sequence for c is a sequence $\underline {\partial } = ( \partial _i)_{i=0}^{\infty }$ of maps $\Gamma _0 \rightarrow \mathbb {Z}$ such that:

1. 1. $\partial _0$ is a nice grading.

2. 2. For all $i>0$ , $\partial _i$ is a $(\partial _0,\ldots , \partial _{i-1})$ -nice grading.

Note that any finite sequence $\{\partial _i\}_{i=1}^n$ satisfying the conditions above can be extended to a nice sequence $\underline {\partial } = \{ \partial _i\}_{i=1}^{\infty }$ by defining $\partial _i = 0$ for $i>n$ (such a completion is not unique).

Definition 4.6. Let $c : \Gamma \rightarrow Q$ be a winding, and let $(\partial _i)$ be a nice sequence for c. If x and y are distinct vertices of $\Gamma $ , we say that $(\partial _i)$ distinguishes x and y if there exists an index $i \in \mathbb {N}$ (depending on x and y) such that $\partial _i(x) \neq \partial _i(y)$ . We say that $(\partial _i)$ distinguishes vertices if it distinguishes each pair of distinct vertices in $\Gamma $ . Of course, if $(\partial _i)$ distinguishes vertices and $\Gamma $ has finitely many vertices, then there exists an $N \in \mathbb {N}$ such that for all distinct x and y, there exists an $i \le N$ satisfying $\partial _i(x) \neq \partial _i(y)$ .

Example 4.7. Let $Q = {\mathbb {L}}_2$ with arrow set $Q_1 = \{\alpha _1,\alpha _2\}$ . Let M be the ${\mathbb {F}}_1$ -representation whose coefficient quiver is the following:

(4.9)

where the winding $c:\Gamma _M \to Q$ sends the blue arrows (resp. red arrows) to $\alpha _1$ (resp. $\alpha _2$ ).

1. 1. One can easily check that the following is a nice grading $\partial _0$ on $ \Gamma _M$ :

   (4.10)

   
   where the numbers on the arrows are $\partial _0(t(\beta ))-\partial _0(s(\beta ))$ for each arrow $\beta $ of $\Gamma _M$ .

2. 2. The following is a $\partial _0$ -nice grading $\partial _1$ on M that is not nice:

   (4.11)

   
   Note that with the grading $\partial _0$ as in (4.10), we only have to consider condition (4.3) when assigning images to the vertices. When building a $\partial _0$ -nice grading as in (4.11), no two arrows satisfy conditions (4.1)–(4.3) simultaneously, so that any integer function on the vertices is permissible. Note that the nice sequence $\underline {\partial } = (\partial _0, \partial _1,0,0,\ldots )$ distinguishes vertices.

Example 4.8. Let $Q = {\mathbb {L}}_3$ with arrow set $Q_1 = \{\alpha _1, \alpha _2, \alpha _3\}$ . In the free group generated by the arrows of Q, set p to be the element

$$ \begin{align*} p = \alpha_1[\alpha_2,\alpha_3]\alpha_1^{-1}[\alpha_3,\alpha_2]\alpha_1[\alpha_3,\alpha_2]\alpha_1^{-1}[\alpha_2,\alpha_3]. \end{align*} $$

Here, $[\gamma ,\delta ] = \gamma \delta \gamma ^{-1}\delta ^{-1}$ is the usual commutator. We may consider p to be a walk in Q, defining an $\mathbb {F}_1$ -representation M whose coefficient quiver is the following:

(4.12)

Using the notational conventions of the previous example, we can define a nice grading $\partial _0$ on M as follows:

(4.13)

We now define a $\partial _0$ -nice grading which is not itself nice. Informally, the conditions (4.1)–(4.3) on a $\partial _0$ -nice grading $\partial _1$ state that whenever two arrows with the same color start at the same number and end at the same number, their increments from the source to the target must be equal. Clearly, all four of the $\alpha _1$ -colored arrows require the same increment. However, one can check that each remaining arrow is only required to share an increment with one other arrow. For instance, the following defines a $\partial _0$ -nice grading $\partial _1$ :

(4.14)

The function $\partial _1$ still fails to distinguish several pairs of vertices, for instance, the first and last vertices of the walk. However, note that any function now qualifies as a $(\partial _0,\partial _1)$ -nice grading. For instance, there are exactly two arrows that start at $2$ and end at $3$ , but one is $\alpha _2$ -colored and the other is $\alpha _3$ -colored: it follows that they violate Condition (4.3), so their increments can be unequal. In particular, we may choose $\partial _2$ to be an injective integer-valued function on the vertices of $\Gamma _M$ . Then, $\partial _2$ will distinguish each pair of vertices of $\Gamma _M$ , and so the nice sequence $(\partial _0, \partial _1,\partial _2,0,0,0,\ldots )$ distinguishes vertices. Note that since $\partial _0$ and $\partial _1$ distinguish some pairs of vertices, there are non-injective choices for $\partial _2$ which still produce a nice sequence distinguishing vertices. However, we will show in Example 5.6 that no choice of $\partial _0$ and $\partial _1$ is enough to distinguish all vertices of $\Gamma _M$ : we say that the nice length of M is equal to $2$ .

Remark 4.9. Let M be an ${\mathbb {F}}_1$ -representation of Q and $F= (\delta _i)_{i\geq 0} $ a nice sequence for M which is finite, in the sense that there exists an $n \in \mathbb {N}$ such that $\delta _i = 0$ for all $i>n$ . Let $( \partial _i)_{i \geq 0}$ be any other nice sequence for M. Then, we can “weave” $(\delta _i)$ and $(\partial _i)$ together to create a new nice sequence $(\partial _i')_{i\geq 0}$ as follows:

1. 1. $\partial _i' = \delta _i$ for $0 \le i \le n$ .

2. 2. $\partial _{i}' = \partial _{i-n-1}$ for $i> n$ .

This is due to the following elementary observation: for any sequence of gradings $\{ \gamma _1,\ldots , \gamma _n\}$ on M and any subset $S \subseteq \{ \gamma _1,\ldots , \gamma _n\}$ (possibly empty), an S-nice grading (defined in the obvious way) is also $(\gamma _1,\ldots , \gamma _n)$ -nice.

In the following, we construct the universal i-nice gradings of a winding $c:\Gamma \to Q$ under which one obtains all nice sequences (Theorem 4.19).

Construction 4.10 (Universal nice grading)

Let $c : \Gamma \rightarrow Q$ be an indecomposable winding (i.e., $\Gamma $ is connected), with M the associated ${\mathbb {F}}_1$ -representation. Then, we have a sequence of maps

(4.15) $$ \begin{align} H_1(\Gamma,\mathbb{Z}) \xrightarrow[]{H_1(c)} H_1(Q,\mathbb{Z}) \xrightarrow[]{\iota} \mathbb{Z}Q_1, \end{align} $$

where $\iota $ is the inclusion map. ¹⁶ Set $\mathcal {V}_M := G/t(G)$ , where $G:= \mathbb {Z}Q_1/\operatorname {Im}(\iota \circ H_1(c)) = \operatorname {coker}(\iota \circ H_1(c))$ and $t(G)$ is the torsion subgroup of G. Since G is a finitely generated abelian group, $G/t(G)$ is a direct summand of G: by abuse of notation, we will use the coset notation of G to denote elements of $\mathcal {V}_M$ . Loosely, one can think of the elements of $\mathcal {V}_M$ as formal $\mathbb {Z}$ -linear combinations of arrows of Q subject to certain linear equations.

Fix a vertex $b \in \Gamma _0$ which we call the basepoint. To each vertex $v \in \Gamma _0$ , we assign an element $X(M)_v \in \mathcal {V}_M$ as follows:

1. 1. If $v = b$ , then $X(M)_v = 0$ .

2. 2. If $v \neq b$ , pick a walk $p = \alpha _1^{\epsilon _1}\cdots \alpha _d^{\epsilon _d}$ from b to v for $\epsilon _j \in \{1,-1\}$ . This is possible because M is indecomposable. Then, set

   $$ \begin{align*} X(M)_v = \sum_{i}{\epsilon_ic(\alpha_i)} + \operatorname{Im}(\iota \circ H_1(c)). \end{align*} $$

Note that $X(M)_v$ does not depend on the choice of walk. The function

$$ \begin{align*} X(M) : \Gamma_0 \rightarrow \mathcal{V}_M \end{align*} $$

$$ \begin{align*} v \mapsto X(M)_v \end{align*} $$

will be called the universal nice grading on M. The image $X(M)_v$ of v is the nice variable associated with v. When there is no chance of confusion, we will denote $X(M)_v$ simply as $X_v$ .

Construction 4.11 (Iterative step)

Let $c : \Gamma \rightarrow Q$ be an indecomposable winding, with M the associated ${\mathbb {F}}_1$ -representation. Let $b \in \Gamma _0$ be a basepoint, and let $X = X(M)$ be the corresponding universal nice grading on M. We define a new quiver $Q^+ = Q^+(M)$ as follows. The vertices of $Q^{+}$ are

$$ \begin{align*} Q^{+}_0 = \{ (X_v,c(v)) \mid v \in \Gamma_0\}. \end{align*} $$

The arrows of $Q^{+}$ are

$$ \begin{align*} Q^{+}_1 = \{ (X_{s(\alpha)}, X_{t(\alpha)}, c(\alpha)) \mid \alpha \in \Gamma_1 \}. \end{align*} $$

To ease notation, we define $\alpha ^{+} := (X_{s(\alpha )}, X_{t(\alpha )}, c(\alpha ))$ . Then the source and target of $\alpha ^{+}$ are as follows:

$$ \begin{align*} s(\alpha^{+}) = (X_{s(\alpha)},c(s(\alpha))), \end{align*} $$

$$ \begin{align*} t(\alpha^{+}) = (X_{t(\alpha)},c(t(\alpha))). \end{align*} $$

Note that $Q^{+}$ is connected. We have quiver maps

$$ \begin{align*} \Gamma \xrightarrow[]{c^+} Q^+ \xrightarrow[]{c^-} Q \end{align*} $$

defined as follows: $c^+$ is the unique quiver morphism which satisfies $c^+(\alpha ) = \alpha ^{+}$ for all $\alpha \in \Gamma _1$ . Since $c^+(\alpha ) = c^+(\beta )$ implies $c(\alpha ) = c(\beta )$ , it is clear that $c^+$ is a winding. Also, note that $c^+$ is surjective on arrows, so that any arrow in $Q^{+}$ can be written as $\alpha ^{+}$ for some $\alpha \in \Gamma _1$ . Then $c^-$ is defined to be the unique quiver morphism satisfying $c^-(\alpha ^{+}) = c(\alpha )$ for all $\alpha \in \Gamma _1$ . Note that $c = c^-c^+$ .

It turns out that $c^-$ is also a winding, which we can see as follows. By the surjectivity of $c^+$ on arrows, it suffices to show that whenever $\alpha , \beta \in \Gamma _1$ satisfy $c(\alpha ) = c(\beta )$ and $\alpha ^{+} \neq \beta ^{+}$ , they also satisfy $s(\alpha ^{+}) \neq s(\beta ^{+})$ and $t(\alpha ^{+}) \neq t(\beta ^{+})$ . If $s(\alpha ^{+}) = s(\beta ^{+})$ , then

$$ \begin{align*} t(\alpha^{+}) & = (X_{t(\alpha)}, c(t(\alpha)) ) \\ & = (X_{s(\alpha)} + c(\alpha), c(t(\alpha))) \\ & = (X_{s(\beta)} + c(\beta), c(t(\beta))) \\ & = t(\beta^{+}). \end{align*} $$

In turn, this implies $\alpha ^{+} = (X_{s(\alpha )}, X_{t(\alpha )}, c(\alpha )) = (X_{s(\beta )}, X_{t(\beta )}, c(\beta )) = \beta ^{+}$ , contrary to hypothesis. The possibility $t(\alpha ^{+}) = t(\beta ^{+})$ can be ruled out in a similar fashion.

Construction 4.12 (Universal i-nice grading)

Let $w : \Gamma \rightarrow Q$ be an indecomposable winding, with R the corresponding $\mathbb {F}_1$ -representation of Q. ¹⁷ Let $b \in \Gamma _0$ be a basepoint, with $X = X(R)$ the universal nice grading of R as in Construction 4.10. Then, Construction 4.11 yields a new indecomposable winding $w^+: \Gamma \rightarrow Q^+$ , whose universal nice grading can be constructed with the same basepoint b. Iterating this process indefinitely yields a sequence of maps that will play a fundamental role in proving the existence (or non-existence) of nice sequences distinguishing the vertices of a given $\mathbb {F}_1$ -representation. More precisely, consider the following algorithm:

1. 1. Set $\sigma ^{(0)} = w$ , $M^{(0)} = R$ , $Q^{(0)} = Q$ , and $\tau ^{(0)} = \operatorname {id}_Q$ (the identity quiver morphism of Q).

2. 2. Suppose that for a fixed $i \in \mathbb {N}$ , an indecomposable winding $\sigma ^{(i)}: \Gamma \rightarrow Q^{(i)}$ with corresponding $\mathbb {F}_1$ -representation $M^{(i)}$ has been defined. Apply Construction 4.10 with $c = \sigma ^{(i)}$ and $M = M^{(i)}$ to define

   $$ \begin{align*} \mathcal{V}^{(i)}_R := \mathcal{V}_{M^{(i)}}, \end{align*} $$
   $$ \begin{align*} X(R)^{(i)}:=X(M^{(i)}). \end{align*} $$

3. 3. Use Construction 4.11 with $c = \sigma ^{(i)}$ and $M = M^{(i)}$ to define

   $$ \begin{align*} Q^{(i+1)} := Q^{(i)+}, \end{align*} $$
   $$ \begin{align*} \sigma^{(i+1)}:=\sigma^{(i)+}, \end{align*} $$
   $$ \begin{align*} \tau^{(i+1)} :=\sigma^{(i)-}. \end{align*} $$
   Furthermore, define $M^{(i+1)}$ to be the indecomposable $\mathbb {F}_1$ -representation corresponding to $\sigma ^{(i+1)}$ .

4. 4. Replace i with $i+1$ and go back to Step 2.

When no confusion will arise, we abbreviate $X(R)^{(i)}$ to $X^{(i)}$ . The image of $v \in \Gamma _0$ under $X^{(i)}$ will be denoted $X^{(i)}_v$ . The function

$$ \begin{align*} X^{(i)} : \Gamma_0 \rightarrow \mathcal{V}^{(i)}_R \end{align*} $$

is called the universal i-nice grading of R. Note that the universal $0$ -nice grading of R is simply the universal nice grading of R. To summarize, this algorithm takes the data $(w,R,b)$ and constructs each of the following (in no particular order):

1. 1. A sequence of finitely generated torsion free abelian groups: $\mathcal {V}^{(0)}_R, \mathcal {V}^{(1)}_R, \mathcal {V}^{(2)}_R,\ldots $ .

2. 2. A function $X^{(i)}: \Gamma _0 \rightarrow \mathcal {V}^{(i)}_R$ for each $i \in \mathbb {N}$ , called the universal i-nice grading of R.

3. 3. A sequence of connected quivers $Q = Q^{(0)}, Q^{(1)}, Q^{(2)}, \ldots $ . We also define $Q^{(-1)} := Q$ for what follows below.

4. 4. An indecomposable winding $\sigma ^{(i)}: \Gamma \rightarrow Q^{(i)}$ for each $i \in \mathbb {N}$ , with $\sigma ^{(0)} = w$ .

5. 5. A winding $\tau ^{(i)}: Q^{(i)} \rightarrow Q^{(i-1)}$ for each $i \in \mathbb {N}$ , satisfying $\sigma ^{(i)} = \tau ^{(i+1)}\sigma ^{(i+1)}$ for all i.

Remark 4.13. The quiver $Q^+$ in Construction 4.11 is adapted directly from the quiver $Q'$ defined in Proposition 6.1 of [7]. The key difference is that $Q'$ depends on a specific nice grading, whereas $Q^+$ only depends on the universal nice grading defined in Construction 4.10. This means that $Q^+$ is a general enough object to study the existence of nice gradings for the associated representation, as we shall see in Theorem 4.19.

Remark 4.14. Use the notation of Construction 4.12. We have now recursively defined $X^{(i)}$ , $Q^{(i)}$ , $\sigma ^{(i)} : \Gamma \rightarrow Q^{(i)}$ , and $\tau ^{(i)}: Q^{(i)} \rightarrow Q^{(i-1)}$ for all $i \geq 0$ , assuming that we define $Q^{(-1)}:=Q$ . For all $v \in \Gamma _0$ , $\alpha \in \Gamma _1$ , and $i \in \mathbb {N}$ , define $v^{(i)} = \sigma ^{(i)}(v)$ and $\alpha ^{(i)} = \sigma ^{(i)}(\alpha )$ . Then, note that for $i \geq 1$ and $\alpha \in \Gamma _1$ , $\tau ^{(i)} : Q^{(i)} \rightarrow Q^{(i-1)}$ satisfies $\tau ^{(i)}(\alpha ^{(i)}) = \alpha ^{(i-1)}$ . Then, we have the following elementary properties:

1. 1. $\sigma ^{(i)} = \tau ^{(i+1)}\sigma ^{(i+1)}$ , for all $i \geq 0$ .

2. 2. $c = \tau ^{(1)}\cdots \tau ^{(i)}\sigma ^{(i)}$ for all $i \geq 1$ .

3. 3. The map $H_1(\tau ^{(i)}) : H_1(Q^{(i)},\mathbb {Z}) \rightarrow H_1(Q^{(i-1)},\mathbb {Z})$ induces a map $\mathcal {V}^{(i)}_M \rightarrow \mathcal {V}^{(i-1)}_M$ (still denoted $H_1(\tau ^{(i)})$ ) that satisfies $H_1(\tau ^{(i)})(X^{(i)}_v) = X^{(i-1)}_v$ for all $v \in \Gamma _0$ and $i \geq 1$ .

4. 4. If $\alpha , \beta \in \Gamma _1$ satisfy $\alpha ^{(k)} = \beta ^{(k)}$ for some $k \geq 1$ , then

   $$ \begin{align*} c(\alpha) = c(\beta), \end{align*} $$
   $$ \begin{align*} X^{(k-1)}_{s(\alpha)} = X^{(k-1)}_{s(\beta)}, \end{align*} $$
   $$ \begin{align*} X^{(k-1)}_{t(\alpha)} = X^{(k-1)}_{t(\beta)} \end{align*} $$
   by the definition of $Q^{(k)}$ . Applying the maps $H_1(\tau ^{(i)})$ for $0 \le i < k$ implies that
   $$ \begin{align*} X^{(i)}_{s(\alpha)} = X^{(i)}_{s(\beta)}, \end{align*} $$
   $$ \begin{align*} X^{(i)}_{t(\alpha)} = X^{(i)}_{t(\beta)}, \end{align*} $$
   for all $0 \le i < k$ .

Example 4.15. Let us compute the i-nice variables for Example 4.7. To begin, let us label the vertices and arrows of $\Gamma := \Gamma _M$ as follows:

where the coloring map $c : \Gamma \rightarrow {\mathbb {L}}_2$ is understood to satisfy $c(\beta _i) = c(\gamma _i) = \alpha _i$ for all $i = 1, 2$ . We will choose $v_1$ as a basepoint throughout. Since $\Gamma $ is a tree, $H_1(\Gamma ,\mathbb {Z}) = 0$ and $\mathcal {V}^{(0)}_M \cong \mathbb {Z}\alpha _1 \oplus \mathbb {Z}\alpha _2$ . Hence, $X^{(0)}$ is the function

$$ \begin{align*} X^{(0)} : \Gamma_0 \rightarrow \mathcal{V}^{(0)}_M \end{align*} $$

$$ \begin{align*} \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array} \right) \mapsto \left( \begin{array}{c} 0 \\ \alpha_1 \\ \alpha_1+\alpha_2 \\ \alpha_2 \\ 0 \end{array} \right). \end{align*} $$

Then, the arrows of $Q^{(1)}$ are described as follows:

$$ \begin{align*} \beta_1^{(1)} = (0,\alpha_1, \alpha_1), \end{align*} $$

$$ \begin{align*} \beta_2^{(1)} = (\alpha_1, \alpha_1+\alpha_2,\alpha_2 ), \end{align*} $$

$$ \begin{align*} \gamma_1^{(1)} = (\alpha_2, \alpha_1+\alpha_2, \alpha_1), \end{align*} $$

$$ \begin{align*} \gamma_2^{(1)} = (0, \alpha_2, \alpha_2). \end{align*} $$

Note that $\sigma ^{(1)} : \Gamma \rightarrow Q^{(1)}$ is injective on arrows, so $Q^{(1)}$ is the quiver:

It follows that $\mathcal {V}^{(1)}_M = \mathbb {Z}\beta _1^{(1)} \oplus \mathbb {Z}\beta _2^{(1)} \oplus \mathbb {Z}\gamma _1^{(1)} \oplus \mathbb {Z}\gamma _2^{(1)} \cong \mathbb {Z}^4$ , and $X^{(1)}$ is the function

$$ \begin{align*} X^{(1)} : \Gamma_0 \rightarrow \mathcal{V}^{(1)}_M \end{align*} $$

$$ \begin{align*} \left(\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right) \mapsto \left(\begin{array}{c} 0 \\ \beta_1^{(1)} \\ \beta_1^{(1)}+\beta_2^{(1)} \\ \beta_1^{(1)}+\beta_2^{(1)} - \gamma_1^{(1)}\\ \beta_1^{(1)}+\beta_2^{(1)} - \gamma_1^{(1)} - \gamma_2^{(1)} \end{array}\right). \end{align*} $$

A similar description holds for all $i \geq 2$ . For all such i, we have $\mathcal {V}^{(i)}_M = \mathbb {Z}\beta _1^{(i)} \oplus \mathbb {Z}\beta _2^{(i)} \oplus \mathbb {Z}\gamma _1^{(i)} \oplus \mathbb {Z}\gamma _2^{(i)} \cong \mathbb {Z}^4$ , and $X^{(i)}$ is the function

$$ \begin{align*} X^{(i)} : \Gamma_0 \rightarrow \mathcal{V}^{(i)}_M \end{align*} $$

$$ \begin{align*} \left(\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right) \mapsto \left(\begin{array}{c} 0 \\ \beta_1^{(i)} \\ \beta_1^{(i)}+\beta_2^{(i)} \\ \beta_1^{(i)}+\beta_2^{(i)} - \gamma_1^{(i)}\\ \beta_1^{(i)}+\beta_2^{(i)} - \gamma_1^{(i)} - \gamma_2^{(i)} \end{array}\right). \end{align*} $$

It will turn out that such behavior is typical whenever $\Gamma $ is a tree.

Example 4.16. Let $Q = {\mathbb {L}}_2$ , and let M be the representation with the following coefficient quiver:

Here, the winding $c : \Gamma \rightarrow {\mathbb {L}}_2$ is understood to satisfy $c(\beta _i) = c(\gamma _i) = \alpha _i$ for $i=1,2$ . We choose $v_1$ to be the basepoint throughout. Note that $\operatorname {Im}(\iota \circ H_1(c)) = \mathbb {Z}(2\alpha _1-2\alpha _2)$ , and so $\mathcal {V}^{(0)}_M$ is the torsion-free quotient of $\frac {\mathbb {Z}\alpha _1\oplus \mathbb {Z}\alpha _2}{\langle 2(\alpha _1-\alpha _2) \rangle } \cong \mathbb {Z} \oplus \mathbb {Z}_2$ . Thus, $\mathcal {V}^{(0)}_M \cong \mathbb {Z}$ , and we will denote the generator corresponding to the coset of $\alpha _1$ by $\alpha $ . The $0$ -nice variables are then described via the function

$$ \begin{align*} X^{(0)} : \Gamma_0 \rightarrow \mathcal{V}^{(0)}_M \end{align*} $$

$$ \begin{align*} \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array} \right)\mapsto \left( \begin{array}{c} 0 \\ \alpha \\ 0 \\ \alpha \end{array} \right). \end{align*} $$

It follows that

where $\bullet $ denotes the unique vertex of ${\mathbb {L}}_2$ . The winding map $\sigma ^{(1)}$ is given by

$$ \begin{align*} \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array} \right)\mapsto \left( \begin{array}{c} (0,\bullet) \\ (\alpha,\bullet) \\ (0,\bullet) \\ (\alpha,\bullet) \end{array} \right), \end{align*} $$

$$ \begin{align*} \left( \begin{array}{c} \beta_1 \\ \beta_2 \\ \gamma_1 \\ \gamma_2 \end{array} \right)\mapsto \left( \begin{array}{c} \beta_1^{(1)} \\ \beta_2^{(1)} \\ \beta_1^{(1)} \\ \beta_2^{(1)} \end{array} \right). \end{align*} $$

Hence, $\mathcal {V}^{(1)}_M$ is the torsion-free quotient of $\frac {\mathbb {Z}\beta _1^{(1)}\oplus \mathbb {Z}\beta _2^{(1)}}{\langle 2(\beta _1^{(1)} - \beta _2^{(1)}) \rangle } \cong \mathbb {Z} \oplus \mathbb {Z}_2$ . Denoting its generator by  $\beta $ , we find that the $1$ -nice variables are given by

$$ \begin{align*} X^{(1)} : \Gamma_0 \rightarrow \mathcal{V}^{(1)}_M \end{align*} $$

$$ \begin{align*} \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array} \right)\mapsto \left( \begin{array}{c} 0 \\ \beta \\ 0 \\ \beta \end{array} \right). \end{align*} $$

We see that for this representation, no new information is obtained from iteration. This reflects the fact that for any nice grading $\partial $ of M, a $\partial $ -nice grading is the same as a nice grading. Note that $v_1$ and $v_3$ cannot be distinguished by any nice sequence, nor can $v_2$ and $v_4$ . This will turn out to be typical behavior for $\Gamma $ a “non-primitive quiver of type $\tilde {\mathbb {A}}_n$ ” (see Definition 5.19).

Definition 4.17. Let M and N be abelian groups. A function $f : M \rightarrow N$ is said to be affine if there exists a $z \in N$ such that $x \mapsto f(x)-z$ is a group homomorphism. If $M = N$ and $f(x) = x+z$ , we say that f is a translation. The translations of M form a group under composition isomorphic to M.

Remark 4.18. Assuming that $c : \Gamma \rightarrow Q$ is indecomposable, the variables $( X^{(i)})_{i \geq 0}$ are unique up to translation in $\mathcal {V}_M^{(i)}$ . Hence, the condition $X^{(i)}_u = X^{(i)}_v$ does not depend on the choice of basepoint.

The following theorem explains the name “universal nice grading” as one obtains any nice sequence as an evaluation of universal nice gradings. In other words, any nice sequence $\underline {\partial }$ uniquely factors through universal nice gradings as follows:

(4.16)

To be precise, we prove the following.

Theorem 4.19. Let M be an indecomposable ${\mathbb {F}}_1$ -representation of Q, and let $c : \Gamma \rightarrow Q$ be the associated winding with basepoint b. Let $\underline {\partial } = (\partial _i)_{i=0}^{\infty }$ be a nice sequence for M. Then, for each i, there exists a unique affine map

$$ \begin{align*} \operatorname{ev}^{(i)}(\underline{\partial}) : \mathcal{V}^{(i)}_M \rightarrow \mathbb{Z} \end{align*} $$

such that $\partial _i = \operatorname {ev}^{(i)}(\underline {\partial }) \circ X^{(i)}$ . We write $X^{(i)}(\underline {\partial }) := \operatorname {ev}^{(i)}(\underline {\partial }) \circ X^{(i)}$ and call it the evaluation of $X^{(i)}$ at $\underline {\partial }$ .

Proof We first prove the claim for $i=0$ . Define a map $g_0 : \mathcal {V}^{(0)}_M \rightarrow \mathbb {Z}$ via the formula

(4.17) $$ \begin{align} \overline{c(\alpha)} \mapsto \partial_0(t(\alpha)) - \partial_0(s(\alpha)), \end{align} $$

where $\alpha \in \Gamma _1$ . We must show that this map is well defined. First, note that $\partial _0 : \Gamma _0 \rightarrow \mathbb {Z}$ extends uniquely to a group map $\mathbb {Z}\Gamma _0 \rightarrow \mathbb {Z}$ (also denoted $\partial _0$ ). Since $\partial _0$ is a nice grading, we have a well-defined map $\hat {g}_0 : \mathbb {Z}Q_1 \rightarrow \mathbb {Z}$ defined via the following formulas:

1. 1. $\hat {g}_0(c(\alpha )) = \partial _0(t(\alpha )) - \partial _0(s(\alpha ))$ , for all $c(\alpha ) \in c(\Gamma _1)$ .

2. 2. $\hat {g}_0(\beta ) = 0$ , for all $\beta \in Q_1\setminus c(\Gamma _1)$ .

If $Z :=\sum {\lambda _{\alpha }\alpha }$ is an element of $H_1(\Gamma ,\mathbb {Z})$ , then

$$ \begin{align*} 0 = \sum{\lambda_{\alpha}[t(\alpha)-s(\alpha)]}, \end{align*} $$

and hence the element $\iota ^{(0)}H_1(c)(Z) = \sum {\lambda _{\alpha }c(\alpha )}$ satisfies

$$ \begin{align*} \hat{g}_0\left(\sum{\lambda_{\alpha}c(\alpha)}\right) & = \sum{\lambda_{\alpha}\hat{g}_0(c(\alpha))}\\ & = \sum{\lambda_{\alpha}[\partial_0(t(\alpha)) - \partial_0(s(\alpha))]} \\ & = \partial_0\left( \sum{\lambda_{\alpha}[t(\alpha)-s(\alpha)]} \right) \\ & = 0. \end{align*} $$

In other words, $\hat {g}_0$ descends to a map on $\mathcal {V}^{(0)}_M$ and $g_0$ is well defined. ¹⁸ We now set

$$ \begin{align*} \operatorname{ev}^{(0)}(\underline{\partial}) := g_0 + \partial_0(b). \end{align*} $$

Let $v \in \Gamma _0$ with $\alpha _1^{\epsilon _1}\cdots \alpha _d^{\epsilon _d}$ a walk in $\Gamma $ from b to v. Then

$$ \begin{align*} \partial_0(v) & = \partial_0(b) + \sum_j{\epsilon_j[\partial_0(t(\alpha_j)) - \partial_0(s(\alpha_j))]} \\ & = \partial_0(b) + g_0\left(\sum_j{\epsilon_jc(\alpha_j)} + \operatorname{Im}(\iota^{(0)}\circ H_1(c)) \right) \\ & = \partial_0(b) + g_0\left(X^{(0)}_v\right) \\ & = [\operatorname{ev}^{(0)}(\underline{\partial})\circ X^{(0)}](v), \end{align*} $$

so we have the desired factorization. To prove uniqueness, suppose $a : \mathcal {V}^{(0)}_M \rightarrow \mathbb {Z}$ is an affine map such that $\partial _0 = a\circ X^{(0)}$ . Then, in particular,

$$ \begin{align*} \operatorname{ev}^{(0)}(\underline{\partial})(0) & = \partial_0(b) \\ & = [a\circ X^{(0)}](b) \\ & = a\left(X^{(0)}_b \right) \\ & = a(0). \end{align*} $$

In other words, $g_0 = \operatorname {ev}^{(0)}(\underline {\partial }) - \partial _0(b)$ and $f := a-\partial _0(b)$ are both group homomorphisms. Pick $\alpha \in \Gamma _1$ and let $ p =\alpha _1^{\epsilon _1}\cdots \alpha _d^{\epsilon _d}$ denote a walk from b to $s(\alpha )$ in $\Gamma $ . Then, $p\alpha $ is a walk from b to $t(\alpha )$ in $\Gamma $ and

$$ \begin{align*} g_0(\overline{c(\alpha)}) & = \partial_0(t(\alpha)) - \partial_0(s(\alpha)) \\ & = \left[g_0\left(X^{(0)}_{t(\alpha)}\right) + \partial_0(b)\right] - \left[g_0\left(X^{(0)}_{s(\alpha)} \right) + \partial_0(b) \right] \\ & = a\left(X^{(0)}_{t(\alpha)}\right) - a\left(X^{(0)}_{s(\alpha)} \right) \\ & = \left[ f\left(X^{(0)}_{t(\alpha)}\right) + \partial_0(b) \right] - \left[ f\left( X^{(0)}_{s(\alpha)} \right) + \partial_0(b) \right] \\ & = f\left( X^{(0)}_{t(\alpha)} - X^{(0)}_{s(\alpha)} \right) \\ & = f(\overline{c(\alpha)}). \end{align*} $$

It follows that $a = \operatorname {ev}^{(0)}(\underline {\partial })$ . Thus, the claim holds for $i = 0$ . Now, suppose that $i> 0$ , and that the result has been proved for all $j < i$ . Since $\partial _0$ is a nice grading for $\sigma ^{(0)} = c$ , we may also assume by induction that $\partial _j$ is a nice grading for $\sigma ^{(j)}$ for all $0 \le j < i$ . Under these assumptions, we claim that $\partial _i$ induces a nice grading on $\sigma ^{(i)}$ . Suppose that $\alpha , \beta \in \Gamma _1$ are given such that $\alpha ^{(i)} = \sigma ^{(i)}(\alpha ) = \sigma ^{(i)}(\beta ) = \beta ^{(i)}$ . Then, by definition of $Q^{(i)}$ , we must have

$$ \begin{align*} c(\alpha) = c(\beta), \end{align*} $$

$$ \begin{align*} X^{(i-1)}_{s(\alpha)} = X^{(i-1)}_{s(\beta)}, \end{align*} $$

$$ \begin{align*} X^{(i-1)}_{t(\alpha)} = X^{(i-1)}_{t(\beta)}. \end{align*} $$

By Remark 4.14, this also implies

$$ \begin{align*} X^{(j)}_{s(\alpha)} = X^{(j)}_{s(\beta)}, \end{align*} $$

$$ \begin{align*} X^{(j)}_{t(\alpha)} = X^{(j)}_{t(\beta)}, \end{align*} $$

for all $0 \le j < i$ . By induction, for all $0 \le j < i$ , there exists a unique affine map $\operatorname {ev}^{(j)}(\underline {\partial }) : \mathcal {V}^{(j)}_M \rightarrow \mathbb {Z}$ satisfying $\partial _j = \operatorname {ev}^{(j)}(\underline {\partial }) \circ X^{(j)}$ . In particular, we must have

$$ \begin{align*} \partial_j(s(\alpha)) & = \operatorname{ev}^{(j)}(\underline{\partial})(X^{(j)}_{s(\alpha)})\\ & = \operatorname{ev}^{(j)}(\underline{\partial})(X^{(j)}_{s(\beta)}) \\ & = \partial_j(s(\beta)), \end{align*} $$

for all $0 \le j < i$ . Similarly, $\partial _j(t(\alpha )) = \partial _j(t(\beta ))$ for all $0 \le j < i$ as well. Since $c(\alpha ) = c(\beta )$ as well, the assumption that $\partial _i$ is a $(\partial _0,\ldots , \partial _{i-1})$ -nice grading implies that

$$ \begin{align*} \partial_i(t(\alpha)) - \partial_i(s(\alpha)) = \partial_i(t(\beta)) - \partial_i (s(\beta)), \end{align*} $$

from which it follows that $\partial _i$ is a nice grading for $\sigma ^{(i)}$ . By the base case, there exists a unique affine map $\operatorname {ev}^{(i)}(\underline {\partial }) : \mathcal {V}^{(0)}_{M^(i)} \rightarrow \mathbb {Z}$ satisfying $\partial _i = \operatorname {ev}^{(i)}(\underline {\partial }) \circ X(M^{(i)})$ . Since $\mathcal {V}^{(i)}_M = \mathcal {V}^{(0)}_{M^{(i)}}$ and $X^{(i)} = X(M^{(i)})$ by Construction 4.12, the result now follows from induction.

The proof above readily implies the following:

Corollary 4.20. Let M be an indecomposable $\mathbb {F}_1$ -representation of Q, and let $c : \Gamma \rightarrow Q$ be the associated winding with basepoint b. Let $(\partial _i)_{i\geq 0}$ be a nice sequence for M. Then, for each i, $\partial _i$ is a nice grading for $\sigma ^{(i)}: \Gamma \rightarrow Q^{(i)}$ .

Remark 4.21. We can view a nice grading as a certain integer-valued function on the arrows of Q. Indeed, a nice grading on M is the same thing as a nice sequence $\underline {\partial } = ( \partial _i)_{i \geq 0}$ with $\partial _i = 0$ for all $i> 0$ . By Theorem 4.19, a nice grading on M is then an affine map $f : \mathcal {V}^{(0)}_M \rightarrow \mathbb {Z}$ . Writing $f = g+z$ with z an integer and $g : \mathcal {V}^{(0)}_M \rightarrow \mathbb {Z}$ a group homomorphism, the map g can be identified with a group homomorphism $\mathbb {Z}Q_1 \rightarrow \mathbb {Z}$ that vanishes on $\operatorname {Im}(\iota \circ H_1(c))$ . If $b_1,\ldots , b_k$ is a cycle basis for $H_1(\Gamma ,\mathbb {Z})$ , then a map $\mathbb {Z}Q_1 \rightarrow \mathbb {Z}$ vanishes on $\operatorname {Im}(\iota \circ H_1(c))$ if and only if it vanishes on $[\iota \circ H_1(c)](b_i)$ for each i. Finally, any such homomorphism comes from a unique function $Q_1 \rightarrow \mathbb {Z}$ .

Corollary 4.22. Let $c : \Gamma \rightarrow Q$ be an indecomposable winding with associated representation M. Let $X^{(i)}$ denote the universal i-nice grading of M. Then, for any two $w, z \in \Gamma _0$ , there exists a nice sequence distinguishing w and z if and only if $X_w^{(i)} \neq X_z^{(i)}$ for some i.

Proof By Theorem 4.19, a nice sequence $\underline {\partial }$ is equivalent to a collection of affine maps $E_i :=\operatorname {ev}^{(i)}(\underline {\partial }): \mathcal {V}_M^{(i)} \rightarrow \mathbb {Z}$ . Write $E_i = h_i + x_i$ , where $h_i : \mathcal {V}_M^{(i)} \rightarrow \mathbb {Z}$ is a group homomorphism and $x_i \in \mathbb {Z}$ . The ith map will distinguish w and z if and only if $E_i(X_w^{(i)}) \neq E_i(X_z^{(i)})$ ; hence, $0 \neq E_i(X_w^{(i)}) - E_i(X_z^{(i)}) = h_i(X_w^{(i)}) - h_i(X_z^{(i)}) = h_i(X_w^{(i)} - X_z^{(i)})$ . This implies that $X_w^{(i)} \neq X_z^{(i)}$ . Conversely, assume that $X_w^{(i)} \neq X_z^{(i)}$ . Since $\mathcal {V}^{(i)}_M$ is a finitely generated torsion-free abelian group, it is free abelian and hence has a basis $\{ b_1,\ldots , b_m\}$ . If $b_i^* : \mathcal {V}^{(i)}_M \rightarrow \mathbb {Z}$ is the homomorphism defined by $b_i^*(b_j) = \delta _{ij}$ , then $X_w^{(i)} \neq X_z^{(i)}$ implies $b_j^*(X_w^{(i)}) \neq b_j^*(X_z^{(i)})$ for some j. Setting $E_i = b_j$ and $E_{k} = 0$ for all $k \neq 0$ , $\{ E_k \}_{k \geq 0}$ is a collection of affine maps which induce a nice sequence distinguishing w and z.

5 Euler characteristics of quiver Grassmannians

5.1 Nice representations

Our reason for considering nice sequences for ${\mathbb {F}}_1$ -representations is that, under certain circumstances, they allow us to combinatorially compute the Euler characteristics of associated quiver Grassmannians. In this section, we introduce the notion of a nice ${\mathbb {F}}_1$ -representation of Q. If M is a nice ${\mathbb {F}}_1$ -representation, then the Euler characteristic of $\operatorname {Gr}_{\mathbf {e}}^Q(M_{\mathbb {C}})$ , the quiver Grassmannian associated with the $\mathbb {C}$ -representation $M_{\mathbb {C}}$ of Q, ¹⁹ can be computed as the number of $\mathbf {e}$ -dimensional subrepresentations of M. This is a combinatorial task, since M is a finite set. We prove several sufficient conditions for M to be nice: more precisely, we prove sufficient conditions for the existence of a nice sequence on M distinguishing vertices. We formalize this idea with the nice length of a representation, which we use to construct new Hopf algebras from $H_Q$ and $H_{Q,{\operatorname {nil}}}$ in §6.2. We conclude this subsection with several examples of nice representations, including a family of nice representations for $Q = {\mathbb {L}}_2$ whose cycle spaces can have arbitrarily high rank. Previously in the literature, only tree modules, band modules, and representations of nice length $0$ had been explicitly considered. The above discussion motivates the following definition.

Definition 5.1. Let M be an ${\mathbb {F}}_1$ -representation of Q with associated winding

$$ \begin{align*} c_M : \Gamma_M \rightarrow Q. \end{align*} $$

We say that M is nice if the following equation holds, for all dimension vectors $\mathbf {e} \leq \mathbf {{dim}}(M)$ :

(5.1) $$ \begin{align} \chi_{\mathbf{e}}(M_{\mathbb{C}}) = |\{ N \le M \mid \mathbf{{dim}}(N) = \mathbf{e} \}|, \end{align} $$

where $\chi _{\mathbf {e}}(M_{\mathbb {C}})$ is the Euler characteristic of $\operatorname {Gr}_{\mathbf {e}}^Q(M_{\mathbb {C}})$ .

In what follows, we will simply denote $\operatorname {Gr}_{\mathbf {e}}^Q(M_{\mathbb {C}})$ by $\operatorname {Gr}_{\mathbf {e}}(M_{\mathbb {C}})$ whenever there is no possible confusion.

In Lemma 1 of [1], Cerulli Irelli shows that a nice grading on a string module M induces an algebraic action of $\mathbb {C}^{\times }$ on $\operatorname {Gr}_{\mathbf {{e}}}(M)$ for each dimension vector $\mathbf {{e}}$ . Writing $M = \bigoplus _{i\in Q_0}{M_i}$ , this action has finitely many fixed points when the grading distinguishes the basis elements of $M_i$ for each i, in which case the number of fixed points equals $\chi _{\mathbf {{e}}}(M)$ . In Theorem 1.1 of [7], Haupt generalizes this result to arbitrary representations and gradings. As a special case, Lemma 4.11 and Corollary 5.2 of [7] show how $(\partial _0,\ldots , \partial _i$ )-nice gradings distinguishing basis elements can be used to compute Euler characteristics of quiver Grassmannians by counting fixed points of the induced torus actions. Haupt then applies these results to tree and band modules. The proposition below is essentially a restatement of the result on Euler characteristics from [7]. We include a proof for the convenience of the reader.

Proposition 5.2 [7]

Let M be an ${\mathbb {F}}_1$ -representation of Q, and let $\underline {\partial }$ be a nice sequence for M which distinguishes vertices. Then, M is a nice representation.

Proof Note that $\Gamma _M$ can be considered as a coefficient quiver of $M_{\mathbb {C}}$ in the sense of Ringel [24] with a choice of a basis as follows: ²⁰

(5.2) $$ \begin{align} \mathcal{B}=\bigsqcup_{v \in Q_0}B_v, \qquad B(v)=M_v \backslash \{0\}. \end{align} $$

Since $\underline {\partial }$ distinguishes vertices, there exists an $n \in \mathbb {N}$ such that for all $x, y \in (\Gamma _M)_0$ , $\partial _i(x) \neq \partial _i(y)$ for some $i\le n$ . In particular, the elements of $M_{\mathbb {C}}$ which are $\partial _i$ -homogeneous (as in [7, p. 756]) for all $i\le n$ are precisely the scalar multiples of elements in the set $\mathcal {B}$ .

Now, it follows from [7, Th. 1.1] that for all $\mathbf {e} \le \mathbf {{dim}}(M)$ , $\operatorname {Gr}_{\mathbf {e}}(M_{\mathbb {C}})$ has the same Euler characteristic as the locally closed subset

(5.3) $$ \begin{align} X = \{N\in \operatorname{Gr}_{\mathbf{e}}(M_{\mathbb{C}})\mid N\text{ has a }\partial_i\text{-homogeneous basis for all }i\le n. \}. \end{align} $$

From the aforementioned correspondence between elements of $M_{\mathbb {C}}$ which are $\partial _i$ -homogeneous and the scalar multiples of elements in $\mathcal {B}$ , any N as in (5.3) must have a basis $\mathcal {B}_N\subseteq \mathcal {B}$ . It is then easy to check that the span of $\mathcal {B}_N$ defines a $\mathbb {C}$ -representation if and only if $\mathcal {B}_N$ is an ${\mathbb {F}}_1$ -representation of Q. ²¹ Hence, X is a finite set with $|\{ N \le M \mid \mathbf {{dim}}(N) = \mathbf {e} \}|$ elements, and so M is nice.

For an ${\mathbb {F}}_1$ -representation M of Q and its subrepresentation N, one can define the quotient $M/N$ by using the quotient of ${\mathbb {F}}_1$ -vector spaces in Definition 2.2. By a subquotient, we mean a quotient of a subrepresentation of M. The following is straightforward.

Proposition 5.3. Let M be an ${\mathbb {F}}_1$ -representation of Q with associated winding $c_M : \Gamma _M \rightarrow Q$ . Let $M'/N'$ denote a subquotient of M with associated winding $c_{M'/N'}$ . If $c_M$ admits a non-degenerate, positive or negative $(\partial _0,\ldots , \partial _n)$ -nice grading, then so does $c_{M'/N'}$ .

Proof It follows from [10, Lem. 3.12] that the coefficient quiver of $M'/N'$ is a subquiver of $\Gamma _M$ . Hence, any non-degenerate/positive/negative $(\partial _0,\ldots , \partial _n)$ -nice grading on M will restrict to one on $M'/N'$ .

Definition 5.4. Let M be an ${\mathbb {F}}_1$ -representation of Q with coefficient quiver $\Gamma := \Gamma _M$ and winding map $c :=c_M$ . Recall from Definition 4.6 that a nice sequence $(\partial _i)$ for M distinguishes vertices if for each distinct $x,y \in \Gamma _0$ , there exists an $i \in \mathbb {N}$ for which $\partial _i(x) \neq \partial _i(y)$ . We say that M has finite nice length if there exists a nice sequence $(\partial _i)$ for M which distinguishes vertices in finitely many steps, in the sense that there exists an $N \in \mathbb {N}$ such that for all distinct $x,y \in \Gamma _0$ , $\partial _i(x) \neq \partial _i(y)$ for some $i \le N$ . If M has finite nice length, the nice length of M is the smallest nonnegative integer n such that there exists a nice sequence $\underline {\partial } = (\partial _i)_{i=0}^{\infty }$ for which the truncated sequence $(\partial _0,\ldots , \partial _n)$ distinguishes vertices. We write ${\operatorname {nice}}(M) = n$ in this case, and $\operatorname {nice}(M) = \infty $ if M does not have finite nice length.

The following properties are clear from the definition (and Proposition 5.2):

1. 1. If $\operatorname {nice}(M) < \infty $ , then M is nice.

2. 2. If M is an ${\mathbb {F}}_1$ -representation of Q, then $\operatorname {nice}(M'/N) \le \operatorname {nice}(M)$ for any subquotient $M'/N$ of M. In particular, if $\operatorname {nice}(M) < \infty $ , then $\operatorname {nice}(M'/N) < \infty $ .

Example 5.5. Let M be an $\mathbb {F}_1$ -representation of Q, with $\Gamma := \Gamma _M$ and $c:=c_M$ . In Theorem 1 of [1], Cerulli Irelli considers a map $d : \Gamma _0 \rightarrow \mathbb {Z}$ which satisfies the two conditions:

1. (D1) For all $v \in Q_0$ , the function d restricts to an injection on $c^{-1}(v)$ .

2. (D2) The function d is a nice grading on M.

If such a d exists, then certainly $\operatorname {nice}(M) \le 1$ , say by Proposition 6.1 of [7]. In fact, we claim $\operatorname {nice}(M) = 0$ . To do this, we must find an injective nice grading of M. First, note that if $f : Q_0 \rightarrow \mathbb {Z}$ is any function, then f induces a nice grading $f^* : \Gamma _0 \rightarrow \mathbb {Z}$ via the formula $f^*(v) = f(c(v))$ . It is straightforward to check that $d + f^*$ still satisfies (D1) and (D2). Pick an ordering $v_0, \ldots , v_m$ of $Q_0$ , and for each $i = 0, \ldots , m$ , set $B_i := c^{-1}(v_i)$ . Define a function $f : Q_0 \rightarrow \mathbb {Z}$ as follows:

$$ \begin{align*} f(v_i) = 2^i\cdot \max_{u,v \in \Gamma_0}\left({|d(u) - d(v)|} +1 \right), i = 0, \ldots , m. \end{align*} $$

Setting $\partial := d + f^*$ yields a nice grading of M that distinguishes any two vertices of $B_i$ , for $i = 0,\ldots , m$ . If $u \in B_i$ and $v \in B_j$ with $i < j$ , a straightforward computation reveals that $\partial (v) - \partial (u) \geq 1$ . Hence, $\partial $ distinguishes all vertices of $\Gamma $ and $\operatorname {nice}(M) = 0$ , as claimed. Conversely, any representation M with nice length $0$ admits a grading that satisfies (D1) and (D2). Hence, we may identify such ${\mathbb {F}}_1$ -representations as those with nice length $0$ .

Example 5.6. In light of Corollary 4.22, the computation in Example 4.15 shows that the string module described in Example 4.7 has nice length $1$ . Similarly, one can show that the string module described in Example 4.8 has nice length $2$ . Indeed, consider the vertices $a,b,\dots ,i$ defined as follows:

(5.4)

Fixing a as a basepoint, we have

$$ \begin{align*} X^{(0)}_a = X^{(0)}_d = X^{(0)}_e = X^{(0)}_h = X^{(0)}_i = 0, \end{align*} $$

$$ \begin{align*} X^{(0)}_b = X^{(0)}_c = X^{(0)}_f = X^{(0)}_g = \alpha_1. \end{align*} $$

The quiver $Q^{(1)}$ is given as follows:

(5.5)

Here, each vertex is labeled by its $0$ -nice variable, T and D are considered as elements of $H_1(Q^{(1)},\mathbb {Z})$ with the clockwise orientation, and $\lambda $ is an arrow of $Q^{(1)}$ . We now have $X^{(1)}_a = X^{(1)}_i = 0$ , $X^{(1)}_b = \lambda $ , $X^{(1)}_c = \lambda +T$ , $X^{(1)}_d = T$ , $X^{(1)}_e = T+D$ , $X^{(1)}_f = \lambda + T+D$ , $X^{(1)}_g = \lambda +D$ , and $X^{(1)}_h = D$ . Since $X^{(1)}_a = X^{(1)}_i$ , it follows that the nice length of this representation is at least $2$ . Since the nice sequence $(\partial _0, \partial _1,\partial _2, 0,0,\ldots )$ described in Example 4.8 distinguishes vertices, the nice length of this representation is exactly $2$ .

Let $c:\Gamma \to Q$ be a winding and $\alpha \in Q_1$ . In the following, it will be convenient to endow $c^{-1}(\alpha )$ with the structure of a subquiver. We let $c^{-1}(\alpha )$ mean the arrow-induced subquiver of $\Gamma $ whose set of arrows is $\{\beta \in \Gamma _1 \mid c(\beta )=\alpha \}$ and whose vertex set consists of the sources and targets of those $\beta $ .

Proposition 5.7. Let M be an $\mathbb {F}_1$ -representation of Q, and let $c_M : \Gamma _M \rightarrow Q$ denote the associated winding. Let $\partial $ be a nice grading on M. Then, the following hold:

1. 1. If $\partial $ is positive or negative, then M is nilpotent.

2. 2. Suppose that $\partial $ is positive or negative, and that Q has no loops. If for each $\alpha \in Q_1$ , $\partial $ restricts to an injection on the set $\{s(\beta ) \mid \beta \in (\Gamma _M)_1, c_M(\beta ) = \alpha \}$ , then $\operatorname {nice}(M) \le 1$ and M is nice.

3. 3. If $\partial $ is non-degenerate and $c_M^{-1}(\alpha )$ is connected for all $\alpha \in Q_1$ , then $\operatorname {nice}(M)\le 1$ and M is nice.

Proof For (1) and (2), we only prove the case that $\partial $ is positive, as the negative case is similar.

(1) Suppose that $\beta _1\cdots \beta _d$ is an oriented cycle in $\Gamma _M$ with $v:=s(\beta _1) = t(\beta _d)$ . Then,

$$ \begin{align*}\partial(v) = \sum_{i=1}^d{\Delta_{c_M(\beta_i)}^{\partial}}+ \partial(v),\end{align*} $$

which implies $\sum _{i=1}^d{\Delta _{c_M(\beta _i)}^{\partial }} = 0$ , contradicting the positivity of $\partial $ . It follows that $\Gamma _M$ is acyclic, so M is nilpotent.

(2) For each $\alpha \in Q_1$ , let $S_{\alpha }$ denote the subquiver of $\Gamma _M$ whose vertex set is $(\Gamma _M)_0$ and whose arrow set is $A_\alpha :=\{\beta \in (\Gamma _M)_1 \mid c(\beta )=\alpha \}$ . Since Q has no loops, for each $\alpha \in Q_1$ , the connected components of $S_{\alpha }$ are isolated vertices or arrows. Combining this with the assumption that $\partial $ restricts to an injection on $\{ s(\beta ) \mid \beta \in A_\alpha \}$ , it follows that for any two arrows $\beta , \gamma \in A_\alpha $ , we have $\partial (s(\beta )) \neq \partial (s(\gamma ))$ . Then, Conditions (4.1) and (4.3) can never hold simultaneously, and so any grading is a $\partial $ -nice grading. In particular, any injective function $\partial _1 : (\Gamma _M)_0 \rightarrow \mathbb {Z}$ is a $\partial $ -nice grading. Then $(\partial , \partial _1,0,0,0\ldots )$ is a nice sequence for M distinguishing vertices and hence $\operatorname {nice}(M) \le 1$ .

(3) Since $c_M^{-1}(\alpha )$ is connected, it must be an oriented path of length $\geq 0$ . It follows from the non-degeneracy of $\partial $ that for any two vertices $v, w \in c_M^{-1}(\alpha )$ , $\partial (v) \neq \partial (w)$ . Then, there is an injective $\partial $ -nice grading on M, and hence $\operatorname {nice}(M) \le 1$ .

Let $c : \Gamma \rightarrow Q$ and $c' : \Gamma ' \rightarrow Q$ be two winding maps. Suppose that $v \in \Gamma _0$ and $v' \in \Gamma _0'$ satisfy $c(v) = c'(v')$ . Then, one can define the amalgam $\Gamma \sqcup _{v\sim v'}\Gamma '$ and associated quiver map $c\sqcup _{v\sim v'}c' : \Gamma \sqcup _{v\sim v'}\Gamma ' \rightarrow Q$ ²² . Note that if $c(\Gamma _1) \cap c(\Gamma _1') = \emptyset $ , then $c\sqcup _{v\sim v'}c'$ is again a winding. The next proposition shows how nice sequences behave with respect to such amalgams.

Proposition 5.8. Let M and N be $\mathbb {F}_1$ -representations of Q with $c_M : \Gamma _M \rightarrow Q$ and $c_N: \Gamma _N \rightarrow Q$ their associated windings. Suppose that $c_M(\Gamma _M)$ and $c_N(\Gamma _N)$ have disjoint arrow sets, and that there are vertices $u \in (\Gamma _M)_0$ and $v \in (\Gamma _N)_0$ with $c_M(u) = c_N(v)$ . Let A denote the $\mathbb {F}_1$ -representation of Q associated with the amalgam $c_M \sqcup _{u\sim v} : \Gamma _M \sqcup _{u\sim v}\Gamma _N \rightarrow Q$ . If $\operatorname {nice}(M) < \infty $ and $\operatorname {nice}(N)< \infty $ , then $\operatorname {nice}(A) < \infty $ and A is nice.

Proof We will write $\Gamma _A = \Gamma _M \sqcup _{u\sim v}\Gamma _N$ to ease notation. Choose the points u, v, and $u=v$ as basepoints for M, N, and A. Let $X^{(i)}$ , $Y^{(i)}$ , and $Z^{(i)}$ denote the i-nice variables (defined in Construction 4.12) for M, N, and A. Let $\mathcal {B}_M$ and $\mathcal {B}_N$ be the cycle bases of $\Gamma _M$ and $\Gamma _N$ associated with any two spanning trees containing the vertices u and v, respectively. Then, $\mathcal {B}_M \sqcup \mathcal {B}_N$ can be considered as a cycle basis for $\Gamma _A$ . Since $c(\Gamma _M)$ and $c(\Gamma _N)$ have no arrows in common, the inclusions $\Gamma _M \hookrightarrow \Gamma _A$ and $\Gamma _N \hookrightarrow \Gamma _A$ induce a sequence of group isomorphisms

(5.6) $$ \begin{align} \mathcal{V}^{(i)}_A \xrightarrow[\cong]{f^{(i)}} \mathcal{V}^{(i)}_M \oplus \mathcal{V}^{(i)}_N, \end{align} $$

satisfying $f^{(i)}(Z_w^{(i)}) = X^{(i)}_w$ whenever $w \in (\Gamma _M)_0$ and $f^{(i)}(Z_w^{(i)}) = Y_w^{(i)}$ whenever $w \in (\Gamma _N)_0$ . Since any two vertices of $\Gamma _M$ can be distinguished by a nice sequence for M, it follows that they can be distinguished by a nice sequence for A as well. Similarly, any two vertices of $\Gamma _N$ and can be distinguished by a nice sequence for A. By Remark 4.9, one may begin any nice sequence for A with the (finitely many) gradings necessary to distinguish these vertices. Hence, it only remains to show that a vertex $w \in (\Gamma _M)_0$ can be distinguished from a vertex $z \in (\Gamma _N)_0$ by a nice sequence for A. By Corollary 4.22, this is equivalent to showing that $Z^{(i)}_w- Z^{(i)}_z \neq 0$ for some i. If $Z^{(i)}_w- Z^{(i)}_z = 0$ for all i, then $f^{(i)}(Z^{(i)}_w- Z^{(i)}_z) = X^{(i)}_w - Y^{(i)}_z = 0$ for all i as well. But this would imply that $X^{(i)}_w$ and $Y^{(i)}_z$ were both $0$ for all i from the decomposition (5.6). But then w cannot be distinguished from u and z cannot be distinguished from v, a contradiction. Hence, $Z^{(i)}_w - Z^{(i)}_z \neq 0$ for some i, which concludes the proof.

In general, determining the ${\mathbb {F}}_1$ -representations of Q which admit a positive grading is a subtle problem. Below, we describe a family of representations which admit positive and injective nice gradings. In particular, such representations are nice. These representations are interesting because they are defined by windings $c :\Gamma \rightarrow Q$ , where $H_1(\Gamma ,\mathbb {Z})$ can have arbitrarily large rank. The main results of [7] explicitly depend on $\Gamma $ being a tree or a band.

Proposition 5.9. Let M be a nilpotent ${\mathbb {F}}_1$ -representation of Q with associated winding $c_M$ . Suppose that $c_M^{-1}(\alpha )$ is connected for all $\alpha \in Q_1$ , and that $\Gamma _M$ contains a set of $\mathbb {Z}$ -linearly independent ²³ cycles $\{ X_1,\ldots , X_n\}$ with the following properties:

1. (i) The cycles $[\iota \circ H_1(c_M)](X_1)$ , $\ldots , [\iota \circ H_1(c_M)](X_n)$ form a $\mathbb {Q}$ -basis for $\mathbb {Q}\otimes _{\mathbb {Z}}\operatorname {Im}(\iota \circ H_1(c_M))$ , where $\iota \circ H_1(c_M)$ is as in (4.15).

2. (ii) For all i, we can write $X_i = p_i - q_i$ , where $p_i$ and $q_i$ are directed paths of positive length in $\Gamma _M$ with common source and target, but no interior vertices in common.

3. (iii) For each $i\le n$ , either $c_M(p_i)$ or $c_M(q_i)$ consists of arrows that do not appear in $c_M(X_j)$ for $j \neq i$ , where we consider $c_M(X_j)$ as a subquiver of Q.

Then, $\operatorname {nice}(M)\le 1$ and M is nice.

Proof For each i, write $p_i = \alpha _1^{(i)}\cdots \alpha _{d_i}^{(i)}$ and $q_i = \beta _1^{(i)}\cdots \beta _{e_i}^{(i)}$ , where the $\alpha _j^{(i)}$ and $\beta _j^{(i)}$ are arrows in $\Gamma _M$ . For each $i=1,\dots ,n$ , we let $Y_i=[\iota \circ H_1(c_M)](X_i)$ . To begin, note that Property (i) implies that $\{ Y_1,\ldots , Y_n\}$ generates a full-rank subgroup of $\operatorname {Im}(\iota \circ H_1(c_M))$ . This means that for any $x \in \operatorname {Im}(\iota \circ H_1(c_M))$ , there exists a positive integer m such that $mx$ is a $\mathbb {Z}$ -linear combination of $\{Y_1,\ldots , Y_n\}$ . But by Remark 4.21, a nice grading on M may be viewed as a function $ Q_1 \rightarrow \mathbb {Z}$ whose induced group homomorphism $\mathbb {Z}Q_1 \rightarrow \mathbb {Z}$ factors through $\operatorname {Im}(\iota \circ H_1(c_M))$ . Let $\Delta : Q_1 \rightarrow \mathbb {Z}$ be any function such that the induced map (also denoted $\Delta $ ) satisfies $\Delta (Y_i) = 0$ for all i. Then, in particular, $0 = \Delta (mx) = m\Delta (x)$ ; hence, $\Delta (x) = 0$ since m is positive. It now follows from Property (ii) that a nice grading on M is a map $\Delta : Q_1 \rightarrow \mathbb {Z}$ satisfying

$$ \begin{align*} \sum_{j=1}^{d_i}{\Delta(c_M(\alpha_j^{(i)}))} = \sum_{j=1}^{e_i}{\Delta(c_M(\beta_j^{(i)}))}, \text{ for all }i = 1,\ldots , n. \end{align*} $$

We now prove the claim by induction on n. If $n=1$ , then defining $\Delta (\alpha _j^{(1)}) = e_1$ for all $j\le d_1$ , $\Delta (\beta _j^{(1)}) = d_1$ for all $j \le e_1$ , and $\Delta (\alpha ) = 1$ otherwise yields such a map. This $\Delta $ is a positive nice grading, so that since $c_M^{-1}(\alpha )$ is connected for all $\alpha \in Q_1$ , M is nice by Proposition 5.7. Now, suppose the claim holds for all $k < n$ . By induction, we can define a map

$$ \begin{align*} \Delta' : \bigcup_{i<n}{(c_M(X_i))_1} \rightarrow \mathbb{N}\setminus\{0\} \end{align*} $$

such that

(5.7) $$ \begin{align} \sum_{j=1}^{d_i}{\Delta'(c_M(\alpha_j^{(i)}))} = \sum_{j=1}^{e_i}{\Delta'(c_M(\beta_j^{(i)}))},\text{ for all }i<n. \end{align} $$

By multiplying $d_n$ , we have the following:

(5.8) $$ \begin{align} \sum_{j=1}^{d_i}{d_n\Delta'(c_M(\alpha_j^{(i)}))} = \sum_{j=1}^{e_i}{d_n\Delta'(c_M(\beta_j^{(i)}))},\text{ for all }i<n. \end{align} $$

Define the map $\Delta $ to be the scalar multiple $\Delta = d_n\Delta '$ :

(5.9) $$ \begin{align} \Delta : \bigcup_{i<n}{(c_M(X_i))_1} \rightarrow \mathbb{N}\setminus\{0\}, \quad c_M(\alpha^{i}_j) \mapsto d_n\Delta'(c_M(\alpha^{i}_j)). \end{align} $$

After possibly relabeling $p_n$ and $q_n$ , we may assume via Property (iii) that $c_M(p_n)$ contains no arrows in $c_M(X_j)$ for $j<n$ . Furthermore, since $c_M^{-1}(\alpha )$ is connected for all $\alpha \in Q_1$ , Property (i) implies that $c_M(p_n)$ and $c_M(q_n)$ have no arrows in common. Then, the condition that $\Delta $ extends to a nice grading on $\Gamma _M$ is precisely the requirement that there exist integers

• • $\Delta (c_M(\alpha _k^{(n)}))$ for $k = 1,\ldots d_n$ ,

• • $\Delta (c_M(\beta _k^{(n)}))$ , whenever $c_M(\beta _k^{(n)})$ not an arrow in $c_M(X_i)$ with $i<n$ ,

such that

(5.10) $$ \begin{align} \sum_{j=1}^{d_n}{\Delta(c_M(\alpha_j^{(n)}))} = \sum_{j=1}^{e_n}{\Delta(c_M(\beta_j^{(n)}))}. \end{align} $$

We construct such a $\Delta $ as follows: first, for any $c_M(\beta _k^{(n)})$ which are not arrows in $c(X_i)$ ( $i<n$ ), define $\Delta (c_M(\beta _k^{(n)})) = d_n$ . Then, the right-hand side of (5.10) is a positive integer divisible by $d_n$ . Define

$$ \begin{align*} \Delta(c_M(\alpha_j^{(n)})) = \frac{1}{d_n} \sum_{j=1}^{e_n}{\Delta(c_M(\beta_j^{(n)}))}, \text{ for all } j = 1,\ldots , d_n. \end{align*} $$

Finally, define $\Delta (\alpha ) = 1$ for any remaining arrows $\alpha \in Q_1$ . Then, $\Delta $ is a positive grading on M, so that $\operatorname {nice}(M) \le 1$ by Proposition 5.7.

We now illustrate this result with some examples.

Example 5.10. Let $Q = {\mathbb {L}}_3$ . For the sake of illustration, let $\{ \alpha , \beta , \gamma \}$ denote the arrow set of ${\mathbb {L}}_3$ . Then, the representation M with coefficient quiver

satisfies the hypotheses of Proposition 5.9 with

and

Here, we interpret the cycles clockwise so that $[\iota \circ H_1(c_M)](X_1) = 2\gamma - 3\beta $ and $[\iota \circ H_1(c_M)](X_2) = 2(\alpha - \beta )$ . We exclude the cycle

since $[\iota \circ H_1(c_M)](Y) = 4(\alpha - \beta ) = 2[\iota \circ H_1(c_M)](X_2)$ . Note that the one-dimensional subrepresentations of M are precisely the sinks of $\Gamma _M$ . The two-dimensional subrepresentations are either a direct sum of two simples or indecomposable: the indecomposables are parameterized by sets of the form $\{ s, t\}$ , where s and t are vertices of $\Gamma _M$ , t is a sink, and there is exists an arrow $s \xrightarrow []{\alpha } t$ in $\Gamma _M$ . It follows that $\chi _1(M_{\mathbb {C}}) = 2$ and $\chi _2(M_{\mathbb {C}}) = 4$ . Similar considerations allows one to compute the remaining Euler characteristics.

Example 5.11. Let $Q = \mathbb {L}_2$ , the quiver with one vertex and two loops. We will let $(\mathbb {L}_2)_1 = \{\alpha _1, \alpha _2\}$ , with $\alpha _1$ -colored arrows appearing in blue and $\alpha _2$ -colored arrows appearing in red. An $\mathbb {F}_1$ -representation M of Q will be called a $2$ -strand representation if there exists a $2\times d$ -matrix $X = \left ( \begin {array}{cccc} m_1 & m_2 & \cdots & m_d \\ n_1 & n_2 & \cdots & n_d \end {array} \right )$ with entries in $\mathbb {Z}_{>0}$ such that $\Gamma _M$ can be described as follows:

where each colored arrow above represents an oriented path of length $m_i$ (resp. $n_i$ ), and an arrow with no label is allowed to be of arbitrary length. Up to translations, a nice grading on M is a pair $(\Delta _1,\Delta _2) \in \mathbb {Z}^2$ satisfying

$$ \begin{align*} m_i\Delta_1 = n_i\Delta_2,\text{ for all }i = 1,\ldots , d. \end{align*} $$

Using Proposition 5.9, it follows that M admits a positive grading if and only if $\operatorname {rank}(X) = 1$ . Indeed, if $\operatorname {rank}(X) = 1$ , then the columns of X are $\mathbb {Q}$ -linear multiples of each other and $\mathbb {Q}\otimes \operatorname {Im}(\iota \circ H_1(c_M)) = \mathbb {Q}(n_1\alpha _2 - m_1\alpha _1)$ . In this case, we only need

to satisfy the hypotheses of Proposition 5.9. Note that Condition (iii) is vacuous since $n=1$ . If $\operatorname {rank}(X)>1$ , then there exist two columns $\left (\begin {array}{c}m_i \\ n_i\end {array} \right )$ and $\left (\begin {array}{c} m_j \\ n_j \end {array}\right )$ of X that are linearly independent over $\mathbb {Q}$ . In particular,

$$ \begin{align*} \det\left( \begin{array}{cc} m_i & m_j \\ -n_i & -n_j \end{array} \right) = -\det\left( \begin{array}{cc} m_i & m_j \\ n_i & n_j \end{array} \right) \neq 0. \end{align*} $$

Then, $m_i\Delta _1 = n_i\Delta _2$ and $m_j\Delta _1 = n_j\Delta _2$ implies

$$ \begin{align*} \left(\begin{array}{cc} m_i & m_j \\ -n_i & -n_j \end{array} \right) \left(\begin{array}{c} \Delta_1 \\ \Delta_2 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \end{array} \right), \end{align*} $$

which has only the trivial solution $\left (\begin {array}{c} \Delta _1 \\ \Delta _2 \end {array} \right ) = \left ( \begin {array}{c} 0 \\ 0 \end {array} \right )$ .

The following are more explicit examples.

Example 5.12. Let M be a representation $M=(M_0,f_1,f_2)$ of $\mathbb {L}_2$ , where $M_0=\{0, 1,2,3\}$ ,

such that

$$ \begin{align*} f_1(1)=2, \quad f_1(2)=3,\quad f_1(3)=0, \end{align*} $$

and

$$ \begin{align*} f_2(1)=2\quad f_2(2)=3,\quad f_2(3)=0. \end{align*} $$

Then, $\Gamma _M$ can be described as follows ( $f_1$ is in blue and $f_2$ is in red):

Then, $M_{\mathbb {C}}$ is a representation of ${\mathbb {L}}_2$ over $\mathbb {C}$ given as follows:

where

$$ \begin{align*} A=A_1=A_2=\begin{bmatrix} 0 & 0 & 0\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix}. \end{align*} $$

So, in this case, $\mathrm {Gr}_{1}(M_{\mathbb {C}})$ consists of the lines of $\mathbb {C}^3$ invariant under the linear transformation A. One can easily see that this set consists only of the line spanned by the vector $\begin {bmatrix} 0\\ 0\\ 1 \end {bmatrix}$ . It follows that $\chi _{1}(M_{\mathbb {C}})=1$ . On the other hand, following the notation in Example 5.11, M is a $2$ -strand representation in ${\operatorname {Rep}}({\mathbb {L}}_2,{\mathbb {F}}_1)_{{\operatorname {nil}}}$ with associated matrix

$$ \begin{align*} X=\begin{bmatrix} 1 & 1\\ 1 & 1 \end{bmatrix}. \end{align*} $$

It follows from the discussion in Example 5.11 that M is nice, in particular, we have

(5.11) $$ \begin{align} \chi_{1}(M_{\mathbb{C}}) = |\{ N \le M \mid \mathbf{{dim}}(N) = 1 \}|=1. \end{align} $$

When $\mathbf {e}=2$ , one may obtain $\chi _{\mathbf {e}}(M_{\mathbb {C}})=1$ from the duality in $\mathbb {C}$ (or applying the same matrix computation as in the case for $d=1$ ). This is also clear as follows:

(5.12) $$ \begin{align} \chi_{2}(M_{\mathbb{C}}) = |\{ N \le M \mid \mathbf{{dim}}(N) = 2 \}|=1. \end{align} $$

Example 5.13. Let M be a representation $M=(M_0,f_1,f_2)$ of $\mathbb {L}_2$ , where $M_0=\{0, 1,2,3\}$ such that

$$ \begin{align*} f_1(1)=3, \quad f_1(2)=f_1(3)=0, \quad \end{align*} $$

and

$$ \begin{align*} f_2(1)=2\quad f_2(2)=3,\quad f_2(3)=0. \end{align*} $$

Then, $\Gamma _M$ can be described as follows ( $f_1$ is in blue and $f_2$ is in red):

Then, $M_{\mathbb {C}}$ is a representation of ${\mathbb {L}}_2$ over $\mathbb {C}$ given as follows:

where

$$ \begin{align*} A_1=\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 1 & 0 & 0 \end{bmatrix}, \quad A_2=\begin{bmatrix} 0 & 0 & 0\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix}. \end{align*} $$

Again, in this case, $\mathrm {Gr}_{1}(M_{\mathbb {C}})$ consists only of the line spanned by the vector $\begin {bmatrix} 0\\ 0\\ 1 \end {bmatrix}$ . It follows that $\chi _{1}(M_{\mathbb {C}})=1$ . On the other hand, M is a $2$ -strand representation with associated matrix

$$ \begin{align*} X=\begin{bmatrix} 1 \\ 2 \end{bmatrix}. \end{align*} $$

It follows from Example 5.11 that M is nice, and we have

(5.13) $$ \begin{align} \chi_{1}(M_{\mathbb{C}}) = |\{ N \le M \mid \mathbf{{dim}}(N) = 1 \}|=1. \end{align} $$

The following example illustrates how our gluing procedure in Proposition 5.8 creates a nice grading.

Example 5.14. Let $Q = \mathbb {L}_4$ , the quiver with one vertex and four loops. We will write $Q_1 = \{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}$ . Consider the $2$ -strand representation

By the discussion above, there is a nice sequence $\underline {\partial }$ distinguishing its vertices. For instance, if we define $\partial _0$ as

then any map $(\Gamma _M)_0 \rightarrow \mathbb {Z}$ is a $\partial _0$ -nice grading. Hence, we can take $\partial _1(v_i) = i$ for all $i \le 4$ , and set $\partial _j = 0$ for all $j> 1$ .

Now, define N to be the string representation

Note that any vector $(\Delta _1,\Delta _2,\Delta _3,\Delta _4) \in \mathbb {Z}^4$ induces a nice grading on N, but no choice distinguishes $v_1'$ and $v_5'$ . Nevertheless, there is a nice sequence $\underline {\partial }'$ for N which distinguishes its vertices. For instance, we can set

so that any map $(\Gamma _N)_0 \rightarrow \mathbb {Z}$ is a $\partial _0'$ -nice grading. As before, set $\partial _1'(v_i') = i$ for $i \le 5$ and $\partial _j' = 0$ for $j> 1$ .

We can glue M and N by identifying $v_1 = v_1'$ to obtain another representation A:

Proposition 5.8 ensures that A admits a nice sequence which distinguishes vertices.

5.2 Low-dimensional niceness results

In this subsection, we give new proofs of results first published in [1], [7]. These new proofs fix apparent gaps in the proofs of Lemmas 6.3 and 6.4 of [7] (see the Appendix at the end of this article for more details). In particular, we show that an $\mathbb {F}_1$ -representation M of Q is nice if $\Gamma _M$ is either a tree or a (primitive) affine Dynkin quiver of type $\tilde {\mathbb {A}}_n$ . We then apply these results to classify the representations of finite nice length when Q is a pseudotree.

Remark 5.15. Let M be an ${\mathbb {F}}_1$ -representation of Q. Suppose that $S \subseteq \Gamma _M$ is a subquiver that is a deformation retract, and let N denote the representation induced by the restriction of $c_M$ to S. Then, $\Gamma _N = S$ , $H_1(\Gamma _N, \mathbb {Z}) \cong H_1(\Gamma _M, \mathbb {Z})$ , and we can find a cycle basis for $\Gamma _N$ which is also a cycle basis for $\Gamma _M$ . In other words, $H_1(\Gamma _N, \mathbb {Z})$ and $H_1(\Gamma _M, \mathbb {Z})$ correspond to the same subgroup of $\mathbb {Z}Q_1$ . It follows that there is a commutative diagram

(5.14)

where $\psi $ is an isomorphism, $\phi _M = \iota _1 \circ H_1(c_M)$ , and $\iota _N = \iota _2 \circ H_1(c_N)$ , where $\iota _1$ (resp. $\iota _2)$ is the inclusion of the image of $H_1(c_M)$ (resp. $H_1(c_N)$ ) into $\mathbb {Z}Q_1$ . This allows us to identify $\operatorname {coker}(\iota _1\circ H_1(c_M))$ with $\operatorname {coker}(\iota _2\circ H_1(c_N))$ , which in turn allows us to identify nice gradings of M with nice gradings of N. We will make such identifications freely throughout this text.

Recall that any winding $c:\Gamma \to Q$ can be considered as a certain coloring of $\Gamma $ , where $\Gamma _0$ (resp. $\Gamma _1$ ) is colored by $Q_0$ (resp. $Q_1$ ). In what follows, we interchangeably use the terms colored quivers and coefficient quivers.

Lemma 5.16. Let $c_1,\dots ,c_m$ be a basis for $H_1(\Gamma _M)$ . Suppose that v is a vertex of $\Gamma _M$ that lies in none of the cycles $c_1,\ldots , c_m$ . Let $\Gamma _M\setminus \{v\}$ denote the colored subquiver of $\Gamma _M$ obtained by deleting v and all arrows incident to it. Then, $\Gamma _M$ admits a nontrivial (resp. non-degenerate, positive, negative) grading if and only if $\Gamma _M\setminus \{v\}$ does.

Proof Since $\Gamma _M\setminus \{v\}$ is a deformation retract of $\Gamma _M$ , this directly follows from Remark 5.15.

Lemma 5.17. Let $c : \Gamma \rightarrow Q$ be a winding with $\Gamma $ a Dynkin quiver of type $\mathbb {A}_n$ , and let M denote the associated representation. Pick a basepoint $b \in \Gamma _0$ . Then, there exists an N such that for all $i \geq N$ :

1. 1. The universal i-nice grading $X^{(i)} : \Gamma _0 \rightarrow \mathcal {V}^{(i)}_M$ is injective.

2. 2. If the distance from v to b is d, then $X^{(i)}_v$ is a linear combination of d distinct elements of $Q^{(i)}_1$ with nonzero coefficients.

In particular, from Corollary 4.22, $\operatorname {nice}(M)<\infty $ and M is nice.

Proof Write $\Gamma = \alpha _1^{\epsilon _1}\cdots \alpha _{n-1}^{\epsilon _{n-1}}$ throughout. We start by proving the following claim: if there is no such N such that (1) holds for all $i\geq N$ , then $\Gamma $ contains distinct arrows $\beta , \gamma \in \Gamma _1$ with $c(\beta ) = c(\gamma )$ and either $s(\beta ) = s(\gamma )$ or $t(\beta ) = t(\gamma )$ , contradicting the assumption that c is a winding. The cases $n = 2, 3$ can be verified through direct computation. Suppose the claim holds for all $k \leq n$ . If no such N exists, then Corollary 4.22 implies that there exist vertices $u, v \in \Gamma _0$ such that $X^{(i)}_u = X^{(i)}_v$ for all i. Indeed, $X^{(i)}_u \neq X^{(i)}_v$ implies $X^{(i+1)}_u \neq X^{(i+1)}_v$ since $H_1(\tau ^{(i+1)})(X^{(i+1)}_z) = X^{(i)}_z$ for all $z \in \Gamma _0$ (see Remark 4.14). If $\{u,v \} \neq \{ s(\alpha _1^{\epsilon _1}), t(\alpha _{n-1}^{\epsilon _{n-1}}) \}$ , then the claim follows from induction, so without loss of generality assume $u = s(\alpha _1^{\epsilon _1})$ and $v = t(\alpha _{n-1}^{\epsilon _{n-1}})$ . By Remark 4.18, we may assume $b = u$ so that $X^{(i)}_u = X^{(i)}_v = 0$ for all i. Since $\Gamma $ is simply connected as a topological space, $\mathcal {V}^{(i)}_M$ is contained in $\mathbb {Z}Q_1^{(i)}$ for each i. Furthermore,

$$ \begin{align*}0 = X^{(i)}_v = \epsilon_{n-1}\alpha_{n-1}^{(i)} + X^{(i)}_{s(\alpha_{n-1}^{\epsilon_{n-1}})}.\end{align*} $$

This implies that there exists a $j <n-1$ such that the following equations hold for all i:

(5.15) $$ \begin{align} \epsilon_j + \epsilon_{n-1} = 0, \end{align} $$

(5.16) $$ \begin{align} \alpha_j^{(i)} = \alpha_{n-1}^{(i)}. \end{align} $$

Indeed, for each i, it is clear that a j depending on i exists. To prove that j can be chosen independently of i, for each $j< n-1$ , let $S_j = \{ i \in \mathbb {N} \mid $ (5.15) and (5.16) hold for $\alpha _j^{(i)}$ }. By the pigeonhole principle, $S_j$ must be unbounded for a fixed j. But then, (5.16) implies that $\alpha _j^{(i')} = \alpha _{n-1}^{(i')}$ for all $i'<i$ , again using Remark 4.14. It follows that $S_j$ is an unbounded, successor-closed subset of the poset $(\mathbb {N},\le )$ , and so $S_j = \mathbb {N}$ . Having established the existence of such a j, the definition of $Q^{(i)}$ implies

$$ \begin{align*} X^{(i)}_{s(\alpha_j^{\epsilon_j})} = X^{(i)}_{s(\alpha_{n-1}^{\epsilon_{n-1}})}, \end{align*} $$

which in turn implies that the subwalk from $s(\alpha _j^{\epsilon _j})$ to $s(\alpha _{n-1}^{\epsilon _{n-1}})$ contains the desired subquiver by the induction hypothesis. Hence, Claim (1) holds, since $c: \Gamma \rightarrow Q$ is a winding. So, choose an $N'$ such that $X^{(i)}$ is injective for all $i \geq N'$ . Then, by construction, $\sigma ^{(N'+1)}: \Gamma \rightarrow \Gamma ^{(N'+1)}$ will be injective on arrows. Hence, Claims (1) and (2) will hold for $N = N'+1$ .

The following corollary confirms the truth of [7, Lem. 6.3]. See the Appendix at the end of this article for a discussion of the original proof.

Corollary 5.18 (cf. Lemma 6.3 of [7])

Let $c : \Gamma \rightarrow Q$ be a winding with associated representation M. Suppose that $\Gamma $ is a tree. Then, $\operatorname {nice}(M)<\infty $ and M is nice.

Proof Suppose that no nice sequence distinguishes $x, y \in \Gamma _0$ . Let p denote the unique walk of minimal length from x to y, and select x as the basepoint. Since $\Gamma $ is retractable, Remark 5.15 implies that the i-nice variables of vertices in p are the same for c and the restricted representation $c|_p$ , for all $i \geq 0$ . In other words, the restricted representation $c|_p : p \rightarrow Q$ cannot distinguish x and y, contradicting Lemma 5.17.

Definition 5.19. Let $c : \Gamma \rightarrow Q$ be a winding with $\Gamma $ an affine Dynkin quiver of type $\tilde {\mathbb {A}}_n$ . Write $\Gamma = \beta _1^{\delta _1}\cdots \beta _d^{\delta _d}$ , where $s(\beta _1^{\delta _1}) = t(\beta _d^{\delta _d})$ . If the cycle $c(\Gamma )$ is primitive (in the sense that $c(\Gamma ) = c(\beta _1)^{\delta _1}\cdots c(\beta _d)^{\delta _d} \neq q^{k}$ for a cycle q of Q with $k>1$ ), then we say that c is primitive. We make a similar definition for a cycle in a general winding.

The following lemma confirms the truth of [7, Lem. 6.4] in the case of an $\mathbb {F}_1$ -representation. See the Appendix at the end of this article for a discussion of the original proof.

Theorem 5.20 (cf. Lemma 6.4 of [7])

Let $c : \Gamma \rightarrow Q$ be a winding with $\Gamma $ an affine Dynkin quiver of type $\tilde {\mathbb {A}}_n$ . Let M be the associated $\mathbb {F}_1$ -representation of Q. Then, $\operatorname {nice}(M)<\infty $ if and only if c is primitive.

Proof $(\implies )$ Suppose that c is not primitive. Then, there exists a cycle $q = \alpha _1^{\epsilon _1}\cdots \alpha _d^{\epsilon _d}$ in Q such that $c(\Gamma ) = q^k$ for some $k>1$ . Since $c : \Gamma \rightarrow Q$ factors through the inclusion $q \hookrightarrow Q$ , we may assume without loss of generality that $q = Q$ . Then, $c : \Gamma \rightarrow Q$ corresponds to wrapping around the cycle $q k$ -times. In other words, we may write

$$ \begin{align*} \Gamma = \beta_{11}^{\epsilon_1}\beta_{12}^{\epsilon_2}\cdots \beta_{1d}^{\epsilon_d}\beta_{21}^{\epsilon_1}\cdots\beta_{2d}^{\epsilon_d}\cdots\beta_{kd}^{\epsilon_d}, \end{align*} $$

where $\beta _{ij} \in \Gamma _1$ satisfies $c(\beta _{ij}) = \alpha _j$ for all i and j. Note that $c(\beta _{i1}^{\epsilon _1}\cdots \beta _{id}^{\epsilon _d}) = c(\beta _{i1}^{\epsilon _1})\cdots c(\beta _{id}^{\epsilon _d})= q$ for all $i \le k$ . Pick $b = s(\beta _{11}^{\epsilon _1})$ as basepoint. Note that $\operatorname {Im}(\iota \circ H_1(c))$ is generated by $c(\Gamma ) = kq \in \mathbb {Z}Q_1$ . It follows that q is torsion in $\mathbb {Z}Q_1/\operatorname {Im}(\iota \circ H_1(c))$ , and so $q = 0$ as an element of $\mathcal {V}^{(0)}_M$ . From this, it follows that

$$ \begin{align*} X^{(0)}_{t(\beta_{ij}^{\epsilon_j})} = \sum_{s=1}^{j}{\epsilon_s\alpha_s}, \end{align*} $$

for all $i \le k$ and $j\le d$ . In particular, $X^{(0)}_{t(\beta _{ij}^{\epsilon _j})} = X^{(0)}_{t(\beta _{1j}^{\epsilon _j})}$ for all $j \le d$ . Note that $\Gamma ^{(1)}$ can then be identified with q, and $\sigma ^{(1)} : \Gamma \rightarrow \Gamma ^{(1)}$ is the map which wraps around $q k$ -times. Repeating the above argument for each $s\geq 0$ , we see that $X^{(s)}_{t(\beta _{ij}^{\epsilon _j})} = X^{(s)}_{t(\beta _{1j}^{\epsilon _j})}$ for all s. It follows that for each $i \le k$ , there is no nice sequence for M distinguishing the vertices $\{ t(\beta _{ij}^{\epsilon _j}) \mid j = 1,\ldots , d \}$ .

$(\impliedby )$ Suppose that c is primitive, but no nice sequence distinguishes the vertices $u, v \in \Gamma _0$ . Let p and q be the two walks (considered as subquivers) in $\Gamma $ from u to v. Suppose that $p = \alpha _1^{\epsilon _1}\cdots \alpha _d^{\epsilon _d}$ and $q^{-1} = \beta _1^{\delta _1}\cdots \beta _e^{\delta _e}$ and that $\ell (p) \le \ell (q)$ , where $\ell (p)$ and $\ell (q)$ are the lengths of p and q, respectively. Without loss of generality, we may assume that u and v are chosen minimal, in the sense that if the distance between $u'$ and $v'$ is strictly less than $\ell (p)$ , then there is a nice sequence which distinguishes $u'$ and $v'$ . We first claim that there must exist an i such that $X^{(i)}_u = X^{(i)}_v$ , but $X^{(i)}_w \not \in \{ X^{(i)}_u,X^{(i)}_v\}$ for all interior vertices $w \in p_0$ . In particular, one has $\{ X^{(i)}_w \mid w \in q_0\} \not \subseteq \{ X^{(i)}_z \mid z \in p_0\}$ . Indeed, to prove the claim, assume by way of contradiction that $\{ X^{(i)}_w \mid w \in q_0\} \subseteq \{ X^{(i)}_z \mid z \in p_0\}$ . We may further assume that $X^{(i)}_v = X^{(i)}_u=0$ . Consider the variables in $q^{-1} = \beta _1^{\delta _1}\cdots \beta _e^{\delta _e}$ starting with the vertex $t(\beta _1^{\delta _1})$ : this vertex is adjacent to $s(\beta _1^{\delta _1}) = v$ , whose i-nice variable is $X^{(i)}_v = 0$ . The only two vertices in p that are adjacent to vertices whose i-nice variables are $0$ , are $t(\alpha _1^{\epsilon _1})$ and $s(\alpha _d^{\epsilon _d})$ : by ${\mathbb {F}}_1$ -linearity ²⁴ $X^{(i)}_{t(\beta _1^{\delta _1})} \neq X^{(i)}_{s(\alpha _d^{\epsilon _d})}$ , so we must have $X^{(i)}_{t(\beta _1^{\delta _1})}= X^{(i)}_{t(\alpha _1^{\epsilon _1})}$ . In particular, this forces $c(\beta _1^{\delta _1}) = c(\alpha _1^{\epsilon _1})$ . We can proceed in this fashion for all vertices of $q^{-1}$ : given any vertex of $q^{-1}$ , there is exactly one way to choose a variable for it from $\{ X^{(i)}_z \mid z \in p_0\}$ which does not contradict ${\mathbb {F}}_1$ -linearity. Thus, we are forced to conclude that $c(q^{-1}) = c(p)^m$ for some m, contradicting primitivity. Hence, there must exist some $w \in q_0$ such that $X^{(i)}_w \not \in \{ X^{(i)}_z \mid z \in p_0\}$ , in particular,

(5.17) $$ \begin{align} \{ X^{(i)}_w \mid w \in q_0\} \not\subseteq \{ X^{(i)}_z \mid z \in p_0\} \end{align} $$

as we wished to show.

Now, we construct a nice sequence distinguishing u and v by using (5.17) which would give us a contradiction. Let T be the tree quiver obtained from $\Gamma $ by splitting v into two separate vertices $\lambda $ and $\rho $ (we will say that p goes from u to $\lambda $ and q goes from u to $\rho $ ). There is a winding map $\tilde {c} : T \rightarrow \Gamma $ which maps $\lambda , \rho \mapsto v$ and acts as the identity on the remaining vertices. This map induces a bijection on arrows, so we identify $T_1$ with $\Gamma _1$ . For each i, let $Y^{(i)}_z$ denote the $0$ -nice variables on the representation $\sigma ^{(i)}\circ \tilde {c}: T \rightarrow Q^{(i)}$ with u as basepoint. Note that $Y^{(i)}_z$ is a coset representative for $X^{(i)}_{\tilde {c}(z)}$ for all i and z. We verify this for the vertices in p: the argument for vertices in q is similar. If $z = t(\alpha _j^{\epsilon _j})$ , then

$$ \begin{align*} Y^{(i)}_z & = \sum_{k=1}^j{\epsilon_k\alpha_k^{(i)}} +\operatorname{Im}\left(\iota^{(i)}\circ H_1(\sigma^{(i)}\circ \tilde{c})\right) \\ & = \sum_{k=1}^j{\epsilon_k\alpha_k^{(i)}} + (0) \in \mathbb{Z}\Gamma^{(i)}_1/(0) \cong \mathbb{Z}\Gamma^{(i)}_1, \end{align*} $$

since T is a tree and hence induces the zero map on homology (note again that we write $\tilde {c}(\alpha _k) = \alpha _k$ since $\tilde {c}$ induces a bijection on arrows). Of course, the walk from u to $\tilde {c}(z)$ in $\Gamma $ is just $\alpha _1^{\epsilon _1}\cdots \alpha _j^{\epsilon _j}$ so that

$$ \begin{align*} X^{(i)}_{\tilde{c}(z)} = \sum_{k=1}^j{\epsilon_k\alpha_k^{(i)}} +\operatorname{Im}\left(\iota^{(i)}\circ H_1(\sigma^{(i)})\right) \end{align*} $$

as claimed. On the other hand, for each $z \in p_0$ (resp. $z \in q_0$ ), the variable $Y^{(i)}_z$ may be identified with the i-nice variable for $\tilde {c}(z)$ with respect to the restricted winding $c|_p$ with basepoint $\tilde {c}(u) = u$ (resp. $c\mid _q$ with basepoint u). By Lemma 5.17, there exists an $i'$ such that the $Y^{(i')}$ are injective on $p_0$ and $q_0$ , and such that $Y^{(i')}_z$ is a sum of t distinct elements of $Q^{(i')}_1$ , where t is the distance from u to z in T (which is the same as the distance from u to $\tilde {c}(z)$ in $\Gamma $ ). Since the arrows of $Q^{(i')}$ are determined by the nice variables $X^{(j)}$ with $j \le i'$ , and since $\{X^{(i)}_w \mid q_0\} \not \subseteq \{X^{(i)}_z \mid z \in p_0 \}$ , it follows that $Y^{(N+1)}_{\rho }$ contains an arrow of $Q^{(N+1)}$ that does not appear in $Y^{(N+1)}_{\lambda }$ , where $N = \max \{i,i'\}$ . In other words, $Y^{(N+1)}_{\rho }$ and $Y^{(N+1)}_{\lambda }$ are linearly independent in $\mathbb {Q}Q^{(N+1)}_1$ . If

$$ \begin{align*}(\pmb{\Delta},Y^{(i)}_z) \mapsto Y^{(i)}_z\mid_{\pmb{\Delta}}\end{align*} $$

denotes the usual pairing

$$ \begin{align*} (\mathbb{Q}Q^{(N+1)}_1)^*\times \mathbb{Q}Q^{(N+1)}_1 \rightarrow \mathbb{Q} \end{align*} $$

induced by $Q^{(N+1)}_1$ and its dual basis, ²⁵ then the $\mathbb {Q}$ -linear map

$$ \begin{align*} (\mathbb{Q}Q^{(N+1)}_1)^* \rightarrow \mathbb{Q}^2 \end{align*} $$

$$ \begin{align*} \pmb{\Delta} \mapsto \left( \begin{array}{c} Y^{(N+1)}_{\lambda}\mid_{\pmb{\Delta}} \\ Y^{(N+1)}_{\rho}\mid_{\pmb{\Delta}} \end{array} \right) \end{align*} $$

has rank $2$ , and so it intersects the diagonal of $\mathbb {Q}^2$ nontrivially. In other words, there is a $\pmb {\Delta } \neq 0$ such that

$$ \begin{align*} Y^{(N+1)}_{\lambda}\mid_{\pmb{\Delta}} = Y^{(N+1)}_{\rho}\mid_{\pmb{\Delta}} \neq 0. \end{align*} $$

If necessary, we can replace $\pmb {\Delta }$ with a suitably large integral multiple to assume that $\pmb {\Delta }$ is an integer vector. In turn, this implies the existence of a nice sequence $\underline {\partial }$ such that

$$ \begin{align*} \partial_{N+1}(v) = \partial_{N+1}(u) + Y^{(N+1)}_{\lambda}\mid_{\pmb{\Delta}}, \end{align*} $$

a contradiction!

If Q is a pseudotree with central cycle C, and M is an indecomposable $\mathbb {F}_1$ -representation of Q, then the restriction $\operatorname {Res}_C(M)$ of M to C is also indecomposable (see [10]). Since indecomposables for C are either (extended) Dynkin quivers of type $\mathbb {A}_n$ or $\tilde {\mathbb {A}}_n$ , it follows from a straightforward argument that $\Gamma _M$ is a pseudotree. Hence, it makes sense to talk about the central cycle of $\Gamma _M$ (if it has one).

Corollary 5.21. Let Q be a pseudotree, and let $c : \Gamma \rightarrow Q$ be a winding with associated representation M. Then, $\operatorname {nice}(M)< \infty $ if and only if the central cycle of $\Gamma _M$ is primitive.

Proof If $\Gamma $ is a tree or of type $\tilde {\mathbb {A}}_n$ , there is nothing to show, so we may assume that $\Gamma $ is a proper pseudotree with central cycle C. First, suppose that C is primitive and hence $\operatorname {Res}_C(M)$ has finite nice length by Theorem 5.20. Note that $\Gamma $ may be obtained by gluing a tree (possibly trivial) to each vertex of C, and that these trees have no arrow colors in common with each other or with C. Since tree representations have finite nice length by Corollary 5.18, the result now follows from Proposition 5.8. The converse is clear from Theorem 5.20.

6 Hall algebras arising from ${\mathbb {F}}_1$ -representations

6.1 Hall algebras and coefficient quivers

In [27], Szczesny discussed the following problem: given a finite graph G and two orientations Q and $Q'$ of G, compare ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ and ${\operatorname {Rep}}(Q',{\mathbb {F}}_1)$ . Note that one cannot appeal to reflection functors, since the usual definition does not make sense over ${\mathbb {F}}_1$ . An alternate strategy would be to compare the associated Hall algebras $H_Q$ and $H_{Q'}$ , or their nilpotent variants $H_{Q,{\operatorname {nil}}}$ and $H_{Q',{\operatorname {nil}}}$ . Since the Milnor–Moore theorem applies to these Hopf algebras, one could even compare their Lie subalgebras of primitive elements. In this section, we study the Lie algebra $\mathfrak {n}_Q$ of $H_{Q,{\operatorname {nil}}}$ when $\overline {Q}$ is a tree or affine Dynkin diagram of type $\tilde {\mathbb {A}}_n$ . Such quivers are precisely the ones of bounded representation type over $\mathbb {F}_1$ [10]. We show that $\mathfrak {n}_Q \cong \mathfrak {n}_{Q'}$ when Q and $Q'$ are different orientations of a tree T, and that if Q is acyclic of type $\tilde {\mathbb {A}}_n$ , then $\mathfrak {n}_Q$ is a central extension of the equioriented quiver of type $\tilde {\mathbb {A}}_n$ . Explicit descriptions of $H_{Q,{\operatorname {nil}}}$ for all Q of type $\tilde {\mathbb {A}}_n$ can then be deduced: previously, only the equioriented case had been described in the literature.

Definition 6.1. Let T be an undirected tree, and let Q be a quiver with $\overline {Q} = T$ . Let $\mathcal {S}_T$ denote the set of nonempty connected subgraphs of T, and let $\mathfrak {n}_T$ denote the free $\mathbb {C}$ -vector space on $\mathcal {S}_T$ .

It was shown in [27, Th. 5] that indecomposable ${\mathbb {F}}_1$ -representations of Q are in bijective correspondence with $\mathcal {S}_T$ . Hence, the underlying vector space of $\mathfrak {n}_Q$ ²⁶ may be identified with  $\mathfrak {n}_T$ . Let the following

$$ \begin{align*} [\cdot,\cdot]_Q : \mathfrak{n}_T\otimes\mathfrak{n}_T \rightarrow \mathfrak{n}_T \end{align*} $$

denote the Lie bracket of $\mathfrak {n}_Q$ , considered as a Lie bracket on $\mathfrak {n}_T$ .

The set $\mathcal {S}_T$ is a poset under the subgraph relation, that is, for $T_1,T_2 \in \mathcal {S}_T T_1 \leq T_2$ if and only if $T_1$ is a subgraph of $T_2$ . Since T is a tree, any two elements $ S, S' \in \mathcal {S}_T$ have a supremum, which we denote by $S\vee S'$ . ²⁷ Indeed, $S\vee S'$ may be characterized as the full subgraph whose vertex set consists of $S_0\cup S^{\prime }_0$ , along with all vertices in the paths joining an element of $S_0$ to $S^{\prime }_0$ .

Of course, the nonempty connected subquivers of Q are in bijective correspondence with the elements of $\mathcal {S}_T$ . By an abuse of notation, we will let S denote the Q-representation corresponding to $S \in \mathcal {S}_T$ and we will write $\Gamma _S = S$ , identifying the coefficient quiver simultaneously with S and the subquiver of Q it determines. Note that if $(S\vee S')_0 = S_0 \sqcup S^{\prime }_0$ , then $S\vee S'$ is obtained by adding exactly one new edge connecting a vertex of S to a vertex of $S'$ .

Definition 6.2. Suppose that $(S\vee S')_0 = S_0 \sqcup S^{\prime }_0$ . Then, we write $S\vee S' = S\xrightarrow []{\alpha } S'$ if $S\vee S'$ , considered as a subquiver of Q, is obtained by adding an $\alpha $ -colored arrow with $s(\alpha ) \in S_0$ and $t(\alpha ) \in S^{\prime }_0$ , where $\alpha \in Q_1$ . We define $S\xleftarrow []{\alpha } S'$ analogously. We write $S\alpha S'$ to mean either $S\xrightarrow []{\alpha }S'$ or $S\xleftarrow []{\alpha }S'$ .

Note that $[S,S']_Q \neq 0$ if and only if $S\vee S' = S\alpha S'$ for some $\alpha \in Q_1$ (see [10, Lem. 3.12(3)]). More specifically, we can write

$$ \begin{align*} [S,S']_Q = \mu_{S,S'}^QS\vee S', \end{align*} $$

where $\mu _{S,S'}^Q \in \mathbb {C}$ is defined via the formula

$$ \begin{align*} \mu_{S,S'}^Q = \begin{cases} +1, & \text{ if }S\vee S' = S\xrightarrow[]{\alpha} S'\text{ for some }\alpha \in Q_1, \\ -1, & \text{ if }S\vee S' = S\xleftarrow[]{\alpha}S'\text{ for some }\alpha \in Q_1,\\ 0, & \text{ otherwise.}\\ \end{cases} \end{align*} $$

Proposition 6.3. Let Q and $Q'$ be different orientations of a tree T. Then, there is an isomorphism $\mathfrak {n}_Q \rightarrow \mathfrak {n}_{Q'}$ .

Proof Let $r_{\alpha }(Q)$ denote the quiver that is obtained from Q by reversing the direction of the arrow $\alpha $ . Then, $Q' = r_{\alpha _k}\cdots r_{\alpha _1}(Q)$ , where $\alpha _1,\ldots ,\alpha _k$ are the arrows of Q that have a different orientation than $Q'$ . The result will therefore follow if we can show $\mathfrak {n}_Q \cong \mathfrak {n}_{r_{\alpha }(Q)}$ for any $\alpha \in Q_1$ , and so without loss of generality we assume that there is an $\alpha $ for which $Q' = r_{\alpha }(Q)$ . Define $\epsilon : \mathcal {S}_T \rightarrow \{ \pm 1\}$ via the formula

$$ \begin{align*} \epsilon(S) = \begin{cases} +1, & \text{ if }\alpha \not\in S_1, \\ -1, & \text{ if }\alpha \in S_1. \end{cases} \end{align*} $$

Here, we identify $\alpha $ with its corresponding (undirected) edge in T. We claim that the $\mathbb {C}$ -linear automorphism $\phi : \mathfrak {n}_T \rightarrow \mathfrak {n}_T$ defined via the formula

$$ \begin{align*} S \mapsto \epsilon(S)S \end{align*} $$

induces an isomorphism $\mathfrak {n}_Q \rightarrow \mathfrak {n}_{Q'}$ . On the one hand,

$$ \begin{align*} \phi\left([S,S']_Q \right) & = \phi\left(\mu_{S,S'}^QS\vee S'\right) \\ & = \epsilon(S\vee S')\mu_{S,S'}^Q S\vee S'. \end{align*} $$

On the other,

$$ \begin{align*} [\phi(S),\phi(S')]_{Q'} & = \epsilon(S)\epsilon(S')[S,S']_{Q'} \\ & = \epsilon(S)\epsilon(S')\mu_{S,S'}^{Q'}S\vee S'. \end{align*} $$

Hence, we will be done if we can show

(6.1) $$ \begin{align} \epsilon(S\vee S')\mu_{S,S'}^Q = \epsilon(S)\epsilon(S')\mu_{S,S'}^{Q'} \end{align} $$

for all $S,S' \in \mathcal {S}_T$ . Note that $\mu _{S,S'}^Q = 0$ if and only if $\mu _{S,S'}^{Q'} = 0$ , so we may assume that neither are zero. There are then two cases to consider:

Case 1: Suppose $S\vee S' = S\beta S'$ for some $\beta \neq \alpha $ . Then, $S\vee S' = S\xrightarrow []{\beta }S'$ in Q if and only if $S\vee S' = S\xrightarrow []{\beta } S'$ in $Q'$ , and $S\vee S' = S\xleftarrow []{\beta }S'$ in Q if and only if $S\vee S' = S\xleftarrow []{\beta }S'$ in $Q'$ . Hence, $\mu _{S,S'}^{Q} = \mu _{S,S'}^{Q'}$ and (6.1) reduces to $\epsilon (S\vee S') = \epsilon (S)\epsilon (S')$ . But since $S\vee S' = S\beta S$ , $\alpha \in (S\vee S')_1$ if and only if $\alpha $ is in exactly one of S or $S'$ . The relation $\epsilon (S\vee S') = \epsilon (S)\epsilon (S')$ now readily follows.

Case 2: Suppose $S\vee S' = S\alpha S'$ . Then, $S\vee S' = S\xrightarrow []{\alpha }S'$ in Q if and only if $S\vee S' = S\xleftarrow []{\alpha } S'$ in $Q'$ , and $S\vee S' = S\xleftarrow []{\alpha }S'$ in Q if and only if $S\vee S' = S\xrightarrow []{\alpha }S'$ in $Q'$ . Hence, $\mu _{S,S'}^{Q} = -\mu _{S,S'}^{Q'}$ and (6.1) reduces to $\epsilon (S\vee S') = -\epsilon (S)\epsilon (S')$ . But $\epsilon (S) = \epsilon (S') = +1$ and $\epsilon (S\vee S') = -1$ for $S\vee S' = S\alpha S'$ , so the equality is clear.

We have proved that (6.1) holds for all S and $S'$ , so $\phi $ is indeed an isomorphism of Lie algebras.

Remark 6.4. Szczesny proved in [27, Th. 8] that there is a surjective map $U(\mathfrak {n}_{+}) \rightarrow H_Q$ when $\overline {Q}$ is a tree, and provides an example to show that this map is in general not injective. Here, $\mathfrak {n}_{+}$ denotes the positive part of the symmetric Kac–Moody algebra associated with Q.

Set $\mathfrak {g} := \mathfrak {gl}_n(\mathbb {C})$ and let $\hat {\mathfrak {g}} = \mathfrak {g}[t,t^{-1}] \oplus \mathbb {C}c$ be the associated affine algebra. The bracket of $\hat {\mathfrak {g}}$ is given by the formula

$$ \begin{align*} [x\otimes t^m, y\otimes t^n] = [x,y]\otimes t^{m+n} + \operatorname{tr}(xy)n\delta_{n,-m}c. \end{align*} $$

Then, $\hat {\mathfrak {g}}$ admits a triangular decomposition $\hat {\mathfrak {g}} = \mathfrak {a}_- \oplus \mathfrak {h}_n \oplus \mathfrak {a}_+$ , where $\mathfrak {a}_- = t^{-1}\mathfrak {gl}_n(\mathbb {C})[t^{-1}]\oplus N_-$ , $\mathfrak {h}_n = D_n \oplus \mathbb {C}c$ , $\mathfrak {a}_+ = t\mathfrak {gl}_n(\mathbb {C})[t]\oplus N_+$ , and $N_-$ , $D_n$ , $N_+$ denote the upper triangular, diagonal, and lower triangular matrices in $\mathfrak {gl}_n(\mathbb {C})$ , respectively.

Recall that if Q is a type $\tilde {\mathbb {A}}_n$ quiver, with vertices oriented cyclically as $1,\ldots , n$ , ²⁸ then its nilpotent indecomposables are described through two families: $I_{[d,i]}$ and $\tilde {I}_d$ , where $1 \le i \le n$ and $d\geq 1$ . If Q is equioriented, then only the first family yields nilpotent representations. $I_{[d,i]}$ is an n-dimensional string module, corresponding to wrapping a walk of length $n-1$ around Q starting at the vertex i. For Q acyclic, $\tilde {I}_d$ is a $dn$ -dimensional ${\mathbb {F}}_1$ -band, ²⁹ corresponding to a closed loop around Q which wraps around d times. For further details, we refer the reader to [10, Constructions 5.10 and 5.11]. Here is an example.

Example 6.5. Consider the following acyclic quiver of type $\tilde {\mathbb {A}}_3$ :

Then, as in [10, Construction 5.10], we have $I_{[8,3]}=\{M_1,M_2,M_3\}$ , where

$$ \begin{align*} M_1=\{k \mid 1\leq k \leq 8, k\equiv 1-3+1 (\mathrm{mod} 3)\}=\{2,5,8\}. \end{align*} $$

Similarly, $M_2=\{3,6\}$ and $M_3=\{1,4,7\}$ . The coefficient quiver is as follows:

The coefficient quiver of $\tilde {I}_2$ is as follows:

The following lemma is due to Szczesny [27]. We recall it here for convenience.

Lemma 6.6. Let Q be the equioriented Dynkin quiver of type $\tilde {\mathbb {A}}_n$ . Then, $\mathfrak {n}_Q \cong \mathfrak {a}_{+}$ .

Proof Let $\{ E_{ij}\}_{i,j \le n}$ denote the standard basis for $\mathfrak {g}$ . Then, as in [27, §11], a direct computation verifies that the map

$$ \begin{align*} \psi : \mathfrak{a}_+ \rightarrow \mathfrak{n}_Q \end{align*} $$

$$ \begin{align*} E_{ij}\otimes t^m \mapsto I_{[j-i+mn, i]} \end{align*} $$

is an isomorphism of Lie algebras.

We now turn to a discussion of type $\tilde {\mathbb {A}}_n$ quivers with acyclic orientations. If Q is such a quiver, then its indecomposable $\mathbb {F}_1$ -representations are $I_{[d,i]}$ and $\tilde {I}_d$ , where $1\le i \le n$ and $d \geq 1$ . Note that any short exact sequence $0 \rightarrow N \rightarrow E \rightarrow M \rightarrow 0$ with N or M isomorphic to some $\tilde {I}_d$ necessarily splits. This means that the elements $[\tilde {I}_d]$ are all central in $\mathfrak {n}_Q$ . As the proposition below shows, we can obtain $\mathfrak {n}_Q$ from $\mathfrak {a}_+$ via a central extension.

For the proposition below, we will use $\delta $ ’s to denote indicator functions on subsets of $\{ (i,j) \mid 1 \le i ,j \le n \}$ . Subsets that are defined by equations will be denoted by those equations, for example, $\delta _{i \equiv j (\operatorname {mod} n)}$ is the indicator function for the set $\{ (i,j) \mid i \equiv j (\operatorname {mod} n)\}$ . When n is understood from context, we will just write $i \equiv j$ . The indicator function for the subset $\{ (i,j), (j,i)\}$ will be denoted by the standard Kronecker notation $\delta _{i,j}$ .

Let $Q = \alpha _1^{\epsilon (1)}\cdots \alpha _{n-1}^{\epsilon (n-1)}$ be an acyclic quiver of type $\tilde {\mathbb {A}}_n$ . Furthermore, let $(i,j,q)$ and $(k,l,s)$ be two elements of $\mathbb {N}^3$ such that $1 \le i,j,k,l \le n$ , either $i \le j$ or $q>0$ , and either $k \le l$ or $s>0$ . Then, the representations $I_{[j-i+qn,i]}$ and $I_{[l-k+sn,k]}$ are well defined. One can compute the following identity in $H_Q$ , where we have set $d:= (j+l)-(i+k) + (q+s)n$ to ease notation:

$$ \begin{align*} [I_{[j-i+qn,i]}]\cdot [I_{[l-k+sn,k]}] &= [I_{[l-k+sn,k]}\oplus I_{[j-i+qn,i]}] + \delta _{j,k}\delta _{\epsilon (j-1),1}[I_{[d,i]}]\\& \quad + \delta _{i,l}\delta _{\epsilon (l-1),-1}[I_{[d,k]}] + \delta _{j,k}\delta _{i,l}\delta _{\epsilon (j-1),1}\delta _{\epsilon (l-1),-1}(q+s)[\tilde {I}_{q+s}]. \end{align*} $$

This immediately implies the following computation in $\mathfrak {n}_Q$ :

$$ \begin{align*} \left[[I_{[j-i+qn,i]}], [I_{[l-k+sn,k]}]\right] & = \delta_{j,k}\left( \delta_{\epsilon(j-1),1} - \delta_{\epsilon(j-1),-1} \right)[I_{[d,i]}] \\& \quad + \delta_{i,l}\left( \delta_{\epsilon(l-1),-1} - \delta_{\epsilon(l-1),1} \right)[I_{[d,k]}] \\& \quad + \delta_{j,k}\delta_{i,l}\left( \delta_{\epsilon(k-1),1} \delta_{\epsilon(l-1),-1} - \delta_{\epsilon(l-1),1} \delta_{\epsilon(k-1),-1} \right)(q+s)[\tilde{I}_{q+s}] \\& = \delta_{j,k}\epsilon(j-1)[I_{[d,i]}] - \delta_{i,l}\epsilon(l-1)[I_{[d,k]}] \\& \quad + \delta_{j,k}\delta_{i,l}\delta_{\epsilon(k-1),-\epsilon(l-1)}\epsilon(k-1)(q+s)[\tilde{I}_{q+s}]. \end{align*} $$

We are now ready to identify $\mathfrak {n}_Q$ in the acyclic case.

Proposition 6.7. Let Q be a Dynkin quiver of type $\tilde {\mathbb {A}}_n$ . Define $Z_Q \le \mathfrak {n}_Q$ be the zero ideal when Q is equioriented, and the central ideal spanned by $\{ [\tilde {I}_d] \mid d \geq 1 \}$ otherwise. Then, there is an isomorphism $\mathfrak {n}_Q/Z_Q \cong \mathfrak {a}_+$ . In particular, $\mathfrak {n}_Q$ is a central extension of $\mathfrak {a}_+$ .

Proof Write $Q = \alpha _1^{\epsilon (1)}\cdots \alpha _{n-1}^{\epsilon (n-1)}$ with $\epsilon (i) = \pm 1$ . The equioriented case is already proved by Szczesny (Lemma 6.6). So, we may assume that $\{ \epsilon (i) \mid 1 \le i \le n-1\}$ is not a proper subset of $\{-1, +1\}$ . Let $(i,j,q)$ and $(k,l,s)$ be two elements of $\mathbb {N}^3$ such that $1 \le i,j,k,l\le n$ , either $i \le j$ or $q> 0$ , and either $k \le l$ or $s>0$ . Then, the representations $I_{[j-i+qn,i]}$ and $I_{[l-k+sn,k]}$ are well defined. From the discussion above, we have

(6.2) $$ \begin{align} \left[[I_{[j-i+qn,i]}], [I_{[l-k+sn,k]}]\right] = \delta_{j,k}\epsilon(j-1)[I_{[d,i]}] - \delta_{i,l}\epsilon(l-1)[I_{[d,k]}]+ \lambda_{(i,j,q):(k,l,s)}[\tilde{I}_{q+s}], \end{align} $$

where the coefficient $ \lambda _{(i,j,q):(k,l,s)}$ is given by the formula

(6.3) $$ \begin{align} \lambda_{(i,j,q):(k,l,s)} = \delta_{j,k}\delta_{i,l}\delta_{\epsilon(k-1),-\epsilon(l-1)}\epsilon(k-1)(q+s). \end{align} $$

Then, we define a map $\psi _Q : \mathfrak {a}_+ \rightarrow \mathfrak {n}_Q/Z_Q$ by the formula

(6.4) $$ \begin{align} E_{ij}\otimes t^q \mapsto \epsilon(j-1)I_{[j-i+qn,i]} + Z_Q. \end{align} $$

(6.2) immediately implies that $\psi _Q$ is a Lie algebra morphism. Showing that it is a bijection is essentially the same as in Lemma 6.6.

6.2 The Hall algebra of representations with finite nice length

In this section, we associate a Hall algebra $H_Q^{\operatorname {nice}}$ (resp. $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ ) to the category of (resp. nilpotent) ${\mathbb {F}}_1$ -representations M of Q with $\operatorname {nice}(M)<\infty $ . We then relate these Hall algebras to $H_Q$ and $H_{Q,{\operatorname {nil}}}$ . A description of $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ when Q is a (not-necessarily proper) pseudotree is obtained. In this case, the representations M with $\operatorname {nice}(M)< \infty $ are related to absolutely indecomposable ${\mathbb {F}}_1$ -representations of quivers with bounded representation type over ${\mathbb {F}}_1$ . Absolutely indecomposable ${\mathbb {F}}_1$ -representations remain mysterious for general Q, and will be the subject of a future article.

Recall from §5 that if $\operatorname {nice}(M)<\infty $ , then any subquotient S of M also satisfies $\operatorname {nice}(S)<\infty $ . It follows that the full subcategory ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)^{\operatorname {nice}}$ (resp. ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}^{\operatorname {nice}}$ ) of representations (resp. nilpotent representations) of finite nice length is finitary and proto-exact. Therefore, we can associate with it a Hall algebra $H_Q^{\operatorname {nice}}$ (resp. $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ ).

It is easy to describe $H_Q^{\operatorname {nice}}$ and $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ in terms of $H_Q$ and $H_{Q,{\operatorname {nil}}}$ , respectively.

Proposition 6.8. Let Q be a fixed quiver. Then, the ideal of $H_Q$ (resp. $H_{Q,{\operatorname {nil}}}$ ) generated by representations with infinite nice length is a Hopf ideal, and we have isomorphisms of Hopf algebras:

$$ \begin{align*} H_Q^{\operatorname{nice}} \cong H_Q/\langle [M] \mid \operatorname{nice}(M) = \infty \rangle, \end{align*} $$

$$ \begin{align*} H_{Q,{\operatorname{nil}}}^{\operatorname{nice}} \cong H_{Q,{\operatorname{nil}}}/\langle [M] \mid \operatorname{nice}(M) = \infty \rangle. \end{align*} $$

Proof Set $I = \langle [M] \mid \operatorname {nice}(M) = \infty \rangle \subseteq H_Q$ , the ideal generated by representations with infinite nice length. Note that any element in I can be written as a $\mathbb {C}$ -linear combination of isomorphism classes $[M]$ with $\operatorname {nice}(M) = \infty $ . This follows from the fact that for any short exact sequence

$$ \begin{align*} 0 \rightarrow M_1 \rightarrow M_2 \rightarrow M_3 \rightarrow 0 \end{align*} $$

in ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ , $\operatorname {nice}(M_1) = \infty $ or $\operatorname {nice}(M_3) = \infty $ implies $\operatorname {nice}(M_2) = \infty $ . Hence, I is the vector space with basis given by $\{ [M] \mid \operatorname {nice}(M) = \infty \}$ . Given $[M] \in I$ , we may write $\Delta ([M])$ as

$$ \begin{align*} \Delta([M]) =\sum_{(A,B) \in D_2(M)}{[A]\otimes [B]}, \end{align*} $$

where $D_2(M) = \{ (A,B) \in \operatorname {Iso}(Q)^2 \mid M \cong A\oplus B\}$ . But $M \cong A \oplus B$ if and only if $\Gamma _M$ can be written as the disjoint union of $\Gamma _A$ and $\Gamma _B$ . Then, $\operatorname {nice}(M) = \infty $ implies that either $\operatorname {nice}(A) = \infty $ or $\operatorname {nice}(B) = \infty $ , and hence

$$ \begin{align*} \Delta([M]) =\sum_{(A,B) \in D_2(M)}{[A]\otimes [B]} \in I\otimes H_Q + H_Q \otimes I. \end{align*} $$

It follows that I is a coideal of $H_Q$ . To show that I is invariant under the antipode, simply note that $S([M])$ is a sum of products of the form $[M_1]\cdots [M_k]$ , where $M \cong M_1\oplus \cdots \oplus M_k$ . Then, $[M] \in I$ implies that $[M_i] \in I$ for at least one index i, and hence $S([M]) \in I$ as well. It follows that I is a Hopf ideal, so that $H_Q/I$ is a Hopf algebra.

There is a $\mathbb {C}$ -linear isomorphism $H_Q^{\operatorname {nice}} \rightarrow H_Q/I$ defined by $[M] \mapsto [M] +I$ . This is an algebra morphism, since a short exact sequence in ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)^{\operatorname {nice}}$ is the same as a short exact sequence

$$ \begin{align*} 0 \rightarrow M_1 \rightarrow M_2 \rightarrow M_3 \rightarrow 0 \end{align*} $$

with $\operatorname {nice}(M_i)< \infty $ for all i. It is also a coalgebra morphism, since the direct sum decompositions of M in ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)^{\operatorname {nice}}$ are exactly the direct sum decompositions of M in ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)$ . Hence, we have the desired isomorphism $H_Q^{\operatorname {nice}} \cong H_Q/I$ . The proof for nilpotent representations is similar.

The results from [27] and §6.1 above allow us to compute $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ when Q has bounded representation type over ${\mathbb {F}}_1$ . ³⁰ In this case, indecomposable representations in ${\operatorname {Rep}}(Q,{\mathbb {F}}_1)_{{\operatorname {nil}}}^{\operatorname {nice}}$ are precisely the absolutely indecomposable representations which we define below.

Definition 6.9. Let Q be a quiver, and let M be an $\mathbb {F}_1$ -representation of Q. We say that M is absolutely indecomposable if $M\otimes _{\mathbb {F}_1}k$ is indecomposable for any algebraically closed field k.

If k is a field and Q is a quiver, a k-representation M of Q is said to be thin if the components of the dimension vector $\mathbf {{dim}}(M)$ are either $0$ or $1$ . We have an analogous definition for ${\mathbb {F}}_1$ -representations of Q. If S is a subquiver of Q, then one obtains a thin representation by taking k at each vertex of S, the identity map $k\rightarrow k$ at each arrow of S, and zero spaces and maps at the remaining vertices and arrows. Of course, is a scalar extension of an ${\mathbb {F}}_1$ -representation which we also call . A straightforward computation reveals that , where c is the number of connected components of S. It follows that is indecomposable if and only if S is connected.

Recall from [10] that if Q is an acyclic quiver of type $\tilde {\mathbb {A}}_n$ , then the indecomposable representations are either string modules $I_{[d,i]}$ , whose coefficient quivers are oriented line graphs, or ${\mathbb {F}}_1$ -bands $\tilde {I}_d$ , whose coefficient quivers are of type $\tilde {\mathbb {A}}_{dn}$ (for $d \geq 1$ ).

Corollary 6.10. Let Q be a connected quiver of bounded representation type, and let M be an indecomposable nilpotent $\mathbb {F}_1$ -representation of Q. Then, $\operatorname {nice}(M)<\infty $ if and only if M is absolutely indecomposable. Furthermore, exactly one of the following holds:

1. 1. Q is a tree. In this case, $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}} = H_{Q}^{\operatorname {nice}} = H_{Q,{\operatorname {nil}}} = H_Q$ .

2. 2. Q is equioriented of type $\tilde {\mathbb {A}}_n$ . In this case, $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}} = H_{Q,{\operatorname {nil}}}$ .

3. 3. Q is acyclic of type $\tilde {\mathbb {A}}_n$ . In this case, $\langle [\tilde {I}_d]\mid d>1 \rangle = \langle [M] \mid \operatorname {nice}(M) = \infty \rangle $ and $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}} = H_Q^{\operatorname {nice}} = H_Q/\langle [\tilde {I}_d]\mid d>1 \rangle $ .

Proof Let k be an algebraically closed field, and let M be an indecomposable nilpotent $\mathbb {F}_1$ -representation of Q. In cases (1) and (2), $\Gamma _M$ is a tree and so $\operatorname {nice}(M)<\infty $ by Corollary 5.18. Since $\Gamma _M$ is a tree, $M\otimes _{\mathbb {F}_1}k$ is a tree module and indecomposable [6]. In case (3), $\operatorname {nice}(I_{[d,i]})<\infty $ and $I_{[d,i]}$ is absolutely indecomposable for all d by the same argument. Hence, it only remains to determine which of the $\tilde {I}_d$ are of finite nice length. For $d=1$ , $\tilde {I}_1$ is isomorphic to the thin representation : then $\operatorname {nice}(\tilde {I}_1)< \infty $ and $\tilde {I}_1$ is absolutely indecomposable since Q is connected. For $d>1$ , $\operatorname {nice}(\tilde {I}_d) = \infty $ by Corollary 5.20 and it is straightforward to verify that $\tilde {I}_d\otimes _{\mathbb {F}_1}k$ is decomposable. The claim now follows.

Corollary 6.11. Let Q be a connected proper pseudotree with central cycle C. Let M be an indecomposable nilpotent ${\mathbb {F}}_1$ -representation of Q. Then, the following are equivalent:

1. 1. $\operatorname {nice}(M)< \infty $ .

2. 2. M is a thin module or a tree module.

3. 3. $\operatorname {Res}_C(M)$ is absolutely indecomposable.

In particular, all M with $\operatorname {nice}(M)<\infty $ are absolutely indecomposable.

Proof Clearly, (2) $\Rightarrow $ (1). To prove (1) $\Rightarrow $ (3), first note that the coefficient quiver of $\operatorname {Res}_C(M)$ is a coefficient subquiver of $\Gamma _M$ , so $\operatorname {nice}(M)<\infty $ implies $\operatorname {nice}(\operatorname {Res}_C(M))< \infty $ . The result then follows from Corollary 6.10. To prove (3) $\Rightarrow $ (2), note that $\operatorname {Res}_C(M)$ absolutely indecomposable implies that $\operatorname {Res}_C(M)$ is a tree module or $\tilde {I}_1$ . Then, either M is a tree module or thin, as we wished to show.

Corollary 6.12. Let Q be a connected proper pseudotree with central cycle C. Then, Hall algebra $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}}$ is described as follows:

1. 1. If C is equioriented, then $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}} = H_{Q,{\operatorname {nil}}}$ .

2. 2. If C is not equioriented, then $H_{Q,{\operatorname {nil}}}^{\operatorname {nice}} = H_Q^{\operatorname {nice}} = H_{Q}/\langle [M] \mid \operatorname {Res}_C(M) \cong \tilde {I}_d, d>1 \rangle $ .

Proof If C is equioriented, then every nilpotent indecomposable ${\mathbb {F}}_1$ -representation is a tree module. If C is not equioriented, then Q is acyclic and the claim follows from Corollary 6.11(3).

Let Q be a connected proper pseudotree. Then, an absolutely indecomposable ${\mathbb {F}}_1$ -representation does not necessarily have finite nice length as the following example illustrates.

Example 6.13. Let Q be the following proper pseudotree:

Let M be the ${\mathbb {F}}_1$ -representation of Q with the following coefficient quiver:

A routine calculation shows that $M_k$ is indecomposable for any algebraically closed field k. Hence, M is absolutely indecomposable, but $\operatorname {nice}(M) = \infty $ by Corollary 6.11.

Let ${\mathbb {F}}_q$ denote the finite field with q elements. For a quiver Q and dimension vector $\mathbf {d}$ , there are finitely many isomorphism classes of $\mathbf {d}$ -dimensional, absolutely indecomposable ${\mathbb {F}}_q$ -representations of Q. One can then associate a function $A_Q(\mathbf {d},q)$ which counts the isoclasses in each dimension. It is shown in [12] that $A_Q(\mathbf {d},q)$ is a polynomial in q with integer coefficients. These functions are shown to satisfy important combinatorial identities in [9], and the behavior of $A_{{\mathbb {L}}_n}(\mathbf {d},q)$ at $q= 1$ is described via tree modules ³¹ in [8], [14].

It is natural to ask how much of this theory carries over to ${\mathbb {F}}_1$ -representations. Certainly, there are finitely many isomorphism classes of absolutely indecomposable, $\mathbf {d}$ -dimensional ${\mathbb {F}}_1$ -representations of Q. One can then define a counting function $A_Q(\mathbf {d})$ analogous to that of $A_Q(\mathbf {d}, q)$ . Two questions immediately become apparent.

Question 6.1. How can one characterize the absolutely indecomposable ${\mathbb {F}}_1$ -representations of a given quiver Q?

Question 6.2. How can one compute $A_Q(\mathbf {d})$ for a given quiver Q?

One would hope that absolutely indecomposable ${\mathbb {F}}_1$ -representations of Q could be used to interpret the numbers $A_Q(\mathbf {d}, 1)$ . However, no obvious relationship exists between $A_Q(\mathbf {d})$ and $A_Q(\mathbf {d}, 1)$ . This leads us to the following question.

Question 6.3. Let Q be a quiver. Does there exist a finitary category $\mathcal {F}_Q$ and a faithful functor $F: {\operatorname {Rep}}(Q,{\mathbb {F}}_1)\rightarrow \mathcal {F}_Q$ with the following properties?

1. 1. For each field k, there is a functor $G_k : \mathcal {F}_Q \rightarrow {\operatorname {Rep}}(Q,k)$ such that the following diagram commutes:

   

2. 2. For any dimension vector $\mathbf {d}$ , there is a suitable notion of an absolutely indecomposable, $\mathbf {d}$ -dimensional object in $\mathcal {F}_Q$ .

3. 3. There are finitely many absolutely indecomposable objects in $\mathcal {F}_Q$ for each $\alpha $ , and the associated counting function is precisely $A_Q(\mathbf {d},1)$ .

For instance, one might ask whether $\mathcal {F}_Q$ could be obtained by suitably modifying the category $\mathcal {C}_Q$ described in §3. These questions will be the topic of a future paper.