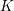Introduction
Algebraic cycles with modulus have been considered to broaden Bloch’s theory of algebraic cycles [Reference BlochBl86]. This concept has arisen from the work by Bloch–Esnault [Reference Bloch and EsnaultBE03], and now it is fully generalized by Binda–Saito in [Reference Binda and SaitoBS17]. The purpose of this paper is to relate Binda–Saito’s theory of algebraic cycles to algebraic
![]() $K$
-theory by establishing a theory of Chern classes. To be precise, we prove the following.
$K$
-theory by establishing a theory of Chern classes. To be precise, we prove the following.
Theorem 0.1. (Theorems 2.26, 3.6)
Let
![]() $X$
be an equidimensional scheme of finite type over a field
$X$
be an equidimensional scheme of finite type over a field
![]() $k$
and
$k$
and
![]() $D$
an effective Cartier divisor on
$D$
an effective Cartier divisor on
![]() $X$
such that
$X$
such that
![]() $X\setminus D$
is smooth over
$X\setminus D$
is smooth over
![]() $k$
. Then, for
$k$
. Then, for
![]() $i,n\geqslant 0$
, there exist maps
$i,n\geqslant 0$
, there exist maps
from the relative algebraic
![]() $K$
-theory to the (Nisnevich) relative motivic cohomology as defined in [Reference Binda and SaitoBS17, Definition 2.10]. These maps are functorial in
$K$
-theory to the (Nisnevich) relative motivic cohomology as defined in [Reference Binda and SaitoBS17, Definition 2.10]. These maps are functorial in
![]() $(X,D)$
in the category of modulus pairs
$(X,D)$
in the category of modulus pairs
![]() $\mathsf{MSm}$
(Definition 1.1) and coincide with Bloch’s Chern classes [Reference BlochBl86, Section 7] when
$\mathsf{MSm}$
(Definition 1.1) and coincide with Bloch’s Chern classes [Reference BlochBl86, Section 7] when
![]() $D=\emptyset$
. Furthermore,
$D=\emptyset$
. Furthermore,
![]() $\mathsf{C}_{n,i}$
are group homomorphisms for
$\mathsf{C}_{n,i}$
are group homomorphisms for
![]() $n>0$
and satisfy the Whitney sum formula for
$n>0$
and satisfy the Whitney sum formula for
![]() $n=0$
.
$n=0$
.
Comparison maps between certain parts of relative algebraic
![]() $K$
-theory and (additive) higher Chow groups with modulus had been constructed in some cases by authors such as Bloch–Esnault, Rülling, Park, Krishna–Levine, Krishna–Park, Krishna, Rülling–Saito and Binda–Krishna [Reference Bloch and EsnaultBE03, Reference RüllingRu07, Reference ParkPa09, Reference Krishna and LevineKL08, Reference Krishna and ParkKP15, Reference KrishnaKr15, Reference Rülling and SaitoRS15, Reference Binda and KrishnaBK18] (to name a few), who reveal profound aspects of those maps. But this is the first time a comparison map has been given on the entire (non-negative) range and in such generality.
$K$
-theory and (additive) higher Chow groups with modulus had been constructed in some cases by authors such as Bloch–Esnault, Rülling, Park, Krishna–Levine, Krishna–Park, Krishna, Rülling–Saito and Binda–Krishna [Reference Bloch and EsnaultBE03, Reference RüllingRu07, Reference ParkPa09, Reference Krishna and LevineKL08, Reference Krishna and ParkKP15, Reference KrishnaKr15, Reference Rülling and SaitoRS15, Reference Binda and KrishnaBK18] (to name a few), who reveal profound aspects of those maps. But this is the first time a comparison map has been given on the entire (non-negative) range and in such generality.
As an application, we give a partial result for the comparison of relative algebraic
![]() $K$
-theory and relative motivic cohomology for henselian dvr.
$K$
-theory and relative motivic cohomology for henselian dvr.
Theorem 0.2. (Theorem 4.3)
Let
![]() $X$
be the spectrum of a henselian dvr over a field of characteristic zero and
$X$
be the spectrum of a henselian dvr over a field of characteristic zero and
![]() $D$
the closed point of
$D$
the closed point of
![]() $X$
seen as a Cartier divisor. Then, for every
$X$
seen as a Cartier divisor. Then, for every
![]() $n\geqslant 0$
, there is a natural isomorphism
$n\geqslant 0$
, there is a natural isomorphism
in the category
![]() $(\text{pro}-\mathsf{Ab})_{\mathbb{Q}}$
of pro-abelian groups up to isogeny.
$(\text{pro}-\mathsf{Ab})_{\mathbb{Q}}$
of pro-abelian groups up to isogeny.
1 Global projective bundle formula
The aim of this section is to formulate and prove a projective bundle formula for the cycle complex with modulus as formulated in Theorem 1.11. It takes place in a very global set-up. As such, it requires a considerable amount of effort to get all the compatibility right just to define the map. Once defined, the proof that it is an isomorphism is then a local problem and already essentially known.
1.1 Modulus pairs and cycle complex presheaves
We begin by the definition of the categories of modulus pairs.
Definition 1.1. Let
![]() $k$
be an arbitrary base field. Denote by
$k$
be an arbitrary base field. Denote by
![]() $\mathsf{MSm}$
the category of pairs
$\mathsf{MSm}$
the category of pairs
![]() $(X,D)$
of an equidimensional
$(X,D)$
of an equidimensional
![]() $k$
-scheme of finite type and an effective Cartier divisor on it, such that
$k$
-scheme of finite type and an effective Cartier divisor on it, such that
![]() $X^{\circ }:=X\setminus D$
is smooth. (Such pairs are commonly called “modulus pairs”.) Morphisms
$X^{\circ }:=X\setminus D$
is smooth. (Such pairs are commonly called “modulus pairs”.) Morphisms
![]() $f\,:\,(X^{\prime },D^{\prime })\rightarrow (X,D)$
are the morphisms of
$f\,:\,(X^{\prime },D^{\prime })\rightarrow (X,D)$
are the morphisms of
![]() $k$
-schemes
$k$
-schemes
![]() $X^{\prime }\rightarrow X$
which restrict to morphisms
$X^{\prime }\rightarrow X$
which restrict to morphisms
![]() $D^{\prime }\rightarrow D$
of subschemes.
$D^{\prime }\rightarrow D$
of subschemes.
We give it a (pre)topology, which we call the Nisnevich topology, by declaring that a family of morphisms
![]() ${\{f_{i}\,:\,(X_{i},D_{i})\rightarrow (X,D)\}}_{i}$
is a covering if and only if the underlying family
${\{f_{i}\,:\,(X_{i},D_{i})\rightarrow (X,D)\}}_{i}$
is a covering if and only if the underlying family
![]() $\{f_{i}\,:\,X_{i}\rightarrow X\}_{i}$
is a Nisnevich cover and
$\{f_{i}\,:\,X_{i}\rightarrow X\}_{i}$
is a Nisnevich cover and
![]() $D_{i}=f_{i}^{\ast }D$
holds for all
$D_{i}=f_{i}^{\ast }D$
holds for all
![]() $i$
.
$i$
.
Remark 1.2. This is not the same as the category denoted by the same symbol in [Reference Kahn, Saito and YamazakiKSY17]. First, we ask the scheme-morphism
![]() $X^{\prime }\rightarrow X$
to be defined on the entire
$X^{\prime }\rightarrow X$
to be defined on the entire
![]() $X^{\prime }$
rather than the open part
$X^{\prime }$
rather than the open part
![]() $X^{\prime \circ }$
. Second, the condition on divisors is also different: for example, the identity morphism on
$X^{\prime \circ }$
. Second, the condition on divisors is also different: for example, the identity morphism on
![]() $X$
induces a morphism
$X$
induces a morphism
![]() $(X,\emptyset )\rightarrow (X,D)$
in our category and
$(X,\emptyset )\rightarrow (X,D)$
in our category and
![]() $(X,D)\rightarrow (X,\emptyset )$
in theirs. We nonetheless opted to use the concise symbol
$(X,D)\rightarrow (X,\emptyset )$
in theirs. We nonetheless opted to use the concise symbol
![]() $\mathsf{MSm}$
.
$\mathsf{MSm}$
.
We would like to have a variant
![]() $\mathsf{MSm}^{\ast }$
of it on which cycle complexes with modulus are functorial. Our specific choice below is not crucial in this work. As another possible choice of
$\mathsf{MSm}^{\ast }$
of it on which cycle complexes with modulus are functorial. Our specific choice below is not crucial in this work. As another possible choice of
![]() $\mathsf{MSm}^{\ast }$
, one could probably take a version of Levine’s
$\mathsf{MSm}^{\ast }$
, one could probably take a version of Levine’s
![]() ${\mathcal{L}}(\text{Sm})$
[Reference LevineLev98, page 9].
${\mathcal{L}}(\text{Sm})$
[Reference LevineLev98, page 9].
Definition 1.3. Fix a category
![]() $\unicode[STIX]{x1D6EC}$
with only finitely many objects and morphisms, and a functor
$\unicode[STIX]{x1D6EC}$
with only finitely many objects and morphisms, and a functor
![]() $F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{MSm}$
;
$F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{MSm}$
;
![]() $\unicode[STIX]{x1D706}\mapsto (X_{\unicode[STIX]{x1D706}},D_{\unicode[STIX]{x1D706}})$
. Let
$\unicode[STIX]{x1D706}\mapsto (X_{\unicode[STIX]{x1D706}},D_{\unicode[STIX]{x1D706}})$
. Let
![]() $\mathsf{MSm}^{\ast }:=\mathsf{MSm}/F$
be the site fibered over
$\mathsf{MSm}^{\ast }:=\mathsf{MSm}/F$
be the site fibered over
![]() $F$
(Definition A.1 via Yoneda), with the additional condition that the underlying morphism
$F$
(Definition A.1 via Yoneda), with the additional condition that the underlying morphism
![]() $f\,:\,X\rightarrow X_{\unicode[STIX]{x1D706}}$
is étale and that
$f\,:\,X\rightarrow X_{\unicode[STIX]{x1D706}}$
is étale and that
![]() $D=f^{\ast }D_{\unicode[STIX]{x1D706}}$
.
$D=f^{\ast }D_{\unicode[STIX]{x1D706}}$
.
Since the dependence on
![]() $F$
does not play a major role in this article, we do not make it explicit in the notation. Note that we have an obvious forgetful functor
$F$
does not play a major role in this article, we do not make it explicit in the notation. Note that we have an obvious forgetful functor
![]() $\mathsf{MSm}^{\ast }\rightarrow \mathsf{MSm}$
given by
$\mathsf{MSm}^{\ast }\rightarrow \mathsf{MSm}$
given by
![]() $((X,D),\unicode[STIX]{x1D706},f)\mapsto (X,D)$
.
$((X,D),\unicode[STIX]{x1D706},f)\mapsto (X,D)$
.
Remark 1.4. The principal case to have in mind is when
![]() $\unicode[STIX]{x1D6EC}$
is just a point. Let
$\unicode[STIX]{x1D6EC}$
is just a point. Let
![]() $(X,D)$
be the value of this point. Then our
$(X,D)$
be the value of this point. Then our
![]() $\mathsf{MSm}^{\ast }$
is nothing but the small Nisnevich site
$\mathsf{MSm}^{\ast }$
is nothing but the small Nisnevich site
![]() $(X,D)_{\text{Nis}}$
. This case is enough for constructing the Chern classes for each pair
$(X,D)_{\text{Nis}}$
. This case is enough for constructing the Chern classes for each pair
![]() $(X,D)$
. To get the functoriality of the Chern classes as in Theorem 0.1, we need to consider the category
$(X,D)$
. To get the functoriality of the Chern classes as in Theorem 0.1, we need to consider the category
![]() $\unicode[STIX]{x1D6EC}=\{\ast \longrightarrow \ast \}$
with a unique nonidentity morphism. Larger
$\unicode[STIX]{x1D6EC}=\{\ast \longrightarrow \ast \}$
with a unique nonidentity morphism. Larger
![]() $\unicode[STIX]{x1D6EC}$
’s may be useful when one considers more involved compatibility.
$\unicode[STIX]{x1D6EC}$
’s may be useful when one considers more involved compatibility.
We refer the reader to [Reference Binda and SaitoBS17] for the definition of Binda–Saito’s cycle complex with modulus
![]() $z^{i}(X|D,\bullet )$
.
$z^{i}(X|D,\bullet )$
.
Definition 1.5. Let
![]() $i\geqslant 0$
be a non-negative integer. For each
$i\geqslant 0$
be a non-negative integer. For each
![]() $((X,D),\unicode[STIX]{x1D706},f)\in \mathsf{MSm}^{\ast }$
, denote by
$((X,D),\unicode[STIX]{x1D706},f)\in \mathsf{MSm}^{\ast }$
, denote by
the subcomplex of cycles
![]() $V\in z^{i}(X|D,n)$
such that for every morphism
$V\in z^{i}(X|D,n)$
such that for every morphism
its pull-back
![]() $g^{\ast }V\in z^{i}(X^{\prime }|D^{\prime },n)$
is well defined. This defines a presheaf
$g^{\ast }V\in z^{i}(X^{\prime }|D^{\prime },n)$
is well defined. This defines a presheaf
![]() $z_{\mathsf{rel}}^{i}$
of complexes on
$z_{\mathsf{rel}}^{i}$
of complexes on
![]() $\mathsf{MSm}^{\ast }$
, which we call the codimension
$\mathsf{MSm}^{\ast }$
, which we call the codimension
![]() $i$
cycle complex presheaf on
$i$
cycle complex presheaf on
![]() $\mathsf{MSm}^{\ast }$
. We remark that by a moving lemma with modulus (Theorem B.1), the inclusion
$\mathsf{MSm}^{\ast }$
. We remark that by a moving lemma with modulus (Theorem B.1), the inclusion
![]() $z_{\mathsf{rel}}^{i}((X,D),\unicode[STIX]{x1D706},f;\bullet )$
$z_{\mathsf{rel}}^{i}((X,D),\unicode[STIX]{x1D706},f;\bullet )$
![]() ${\hookrightarrow}z^{i}(X|D,\bullet )$
is a quasi-isomorphism locally in the Nisnevich topology on each
${\hookrightarrow}z^{i}(X|D,\bullet )$
is a quasi-isomorphism locally in the Nisnevich topology on each
![]() $X$
.
$X$
.
Next, we want to define a presheaf of complexes
![]() $p_{\ast }z_{\mathsf{rel}}^{r}$
which serves as “the cycle complex of the projective bundle associated to the universal vector bundle on
$p_{\ast }z_{\mathsf{rel}}^{r}$
which serves as “the cycle complex of the projective bundle associated to the universal vector bundle on
![]() $B\text{GL}_{r}$
”. Defining it requires some more notation which we now introduce.
$B\text{GL}_{r}$
”. Defining it requires some more notation which we now introduce.
For a non-negative integer
![]() $n\geqslant 0$
, set
$n\geqslant 0$
, set
![]() $[n]=\{0,\ldots ,n\}$
and endow it with the usual order. For a non-negative integer
$[n]=\{0,\ldots ,n\}$
and endow it with the usual order. For a non-negative integer
![]() $r\geqslant 0$
, let us recall (or adopt the convention) that
$r\geqslant 0$
, let us recall (or adopt the convention) that
![]() $B\text{GL}_{r}$
is the simplicial
$B\text{GL}_{r}$
is the simplicial
![]() $k$
-scheme
$k$
-scheme
![]() $B_{n}\text{GL}_{r}:=(\text{GL}_{r})^{n}$
with the structure morphism associated to each ordered map
$B_{n}\text{GL}_{r}:=(\text{GL}_{r})^{n}$
with the structure morphism associated to each ordered map
![]() $\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
:
$\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
:
The simplicial scheme
![]() $B\text{GL}_{r}$
defines a simplicial presheaf on
$B\text{GL}_{r}$
defines a simplicial presheaf on
![]() $\mathsf{MSm}^{\ast }$
by
$\mathsf{MSm}^{\ast }$
by
![]() $((X,D),\unicode[STIX]{x1D706},f)\mapsto B\text{GL}_{r}(X)$
.
$((X,D),\unicode[STIX]{x1D706},f)\mapsto B\text{GL}_{r}(X)$
.
Definition 1.6. Let
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
be the site fibered over
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
be the site fibered over
![]() $B\text{GL}_{r}$
.
$B\text{GL}_{r}$
.
Recall that the simplicial
![]() $k$
-scheme
$k$
-scheme
![]() $\mathbb{P}(E\text{GL}_{r})$
has
$\mathbb{P}(E\text{GL}_{r})$
has
![]() $\mathbb{P}(E_{n}\text{GL}_{r})=\mathbb{P}^{r-1}\times (\text{GL}_{r})^{n}$
as its
$\mathbb{P}(E_{n}\text{GL}_{r})=\mathbb{P}^{r-1}\times (\text{GL}_{r})^{n}$
as its
![]() $n$
th component, and the structure morphism corresponding to
$n$
th component, and the structure morphism corresponding to
![]() $\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
is defined by
$\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
is defined by
where the expression
![]() $z\unicode[STIX]{x1D6FC}$
for
$z\unicode[STIX]{x1D6FC}$
for
![]() $z\in \mathbb{P}^{r-1}$
and
$z\in \mathbb{P}^{r-1}$
and
![]() $\unicode[STIX]{x1D6FC}\in \text{GL}_{r}$
denotes the right action of matrices on row vectors. Write also
$\unicode[STIX]{x1D6FC}\in \text{GL}_{r}$
denotes the right action of matrices on row vectors. Write also
![]() $[\unicode[STIX]{x1D6FC}]\,:\,\mathbb{P}^{r-1}\rightarrow \mathbb{P}^{r-1}$
for this action, so that
$[\unicode[STIX]{x1D6FC}]\,:\,\mathbb{P}^{r-1}\rightarrow \mathbb{P}^{r-1}$
for this action, so that
![]() $[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}]=[\unicode[STIX]{x1D6FD}][\unicode[STIX]{x1D6FC}]$
holds, and
$[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}]=[\unicode[STIX]{x1D6FD}][\unicode[STIX]{x1D6FC}]$
holds, and
![]() $[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}]^{\ast }=[\unicode[STIX]{x1D6FC}]^{\ast }[\unicode[STIX]{x1D6FD}]^{\ast }$
for pull-back operations.
$[\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}]^{\ast }=[\unicode[STIX]{x1D6FC}]^{\ast }[\unicode[STIX]{x1D6FD}]^{\ast }$
for pull-back operations.
Denote by
![]() $p\,:\,\mathbb{P}(E\text{GL}_{r})\rightarrow B\text{GL}_{r}$
the projection. It is a projective bundle with fiber
$p\,:\,\mathbb{P}(E\text{GL}_{r})\rightarrow B\text{GL}_{r}$
the projection. It is a projective bundle with fiber
![]() $\mathbb{P}^{r-1}$
and defines a projective bundle (= a presheaf locally isomorphic to the constant presheaf
$\mathbb{P}^{r-1}$
and defines a projective bundle (= a presheaf locally isomorphic to the constant presheaf
![]() $\mathbb{P}^{r-1}$
) on the category
$\mathbb{P}^{r-1}$
) on the category
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, which motivates the following definition.
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, which motivates the following definition.
Definition 1.7. For each
![]() $i\geqslant 0$
, we define the presheaf
$i\geqslant 0$
, we define the presheaf
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
of complexes on
$p_{\ast }z_{\mathsf{rel}}^{i}$
of complexes on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
as follows: for each object
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
as follows: for each object
![]() $((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, denote by
$((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, denote by
the subcomplex of cycles
![]() $V\in z^{i}(\mathbb{P}^{r-1}\times X|\mathbb{P}^{r-1}\times D,m)$
such that for every morphism
$V\in z^{i}(\mathbb{P}^{r-1}\times X|\mathbb{P}^{r-1}\times D,m)$
such that for every morphism
![]() $(g,\unicode[STIX]{x1D711})\,:\,((X^{\prime },D^{\prime })\unicode[STIX]{x1D706}^{\prime },f^{\prime })\rightarrow ((X,D),\unicode[STIX]{x1D706},f)$
in
$(g,\unicode[STIX]{x1D711})\,:\,((X^{\prime },D^{\prime })\unicode[STIX]{x1D706}^{\prime },f^{\prime })\rightarrow ((X,D),\unicode[STIX]{x1D706},f)$
in
![]() $\mathsf{MSm}^{\ast }$
, its pull-back
$\mathsf{MSm}^{\ast }$
, its pull-back
![]() $(\text{id}_{\mathbb{P}^{r-1}}\times g)^{\ast }V\in z^{i}(\mathbb{P}^{r-1}\times X^{\prime }|\mathbb{P}^{r-1}\times D^{\prime },m)$
is well defined. (This does not depend on the data
$(\text{id}_{\mathbb{P}^{r-1}}\times g)^{\ast }V\in z^{i}(\mathbb{P}^{r-1}\times X^{\prime }|\mathbb{P}^{r-1}\times D^{\prime },m)$
is well defined. (This does not depend on the data
![]() $(n,\unicode[STIX]{x1D6FC})$
.)
$(n,\unicode[STIX]{x1D6FC})$
.)
Given a morphism
![]() $(g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D703})\,:\,((X^{\prime },D^{\prime }),\unicode[STIX]{x1D706}^{\prime },f^{\prime };n^{\prime },\unicode[STIX]{x1D6FC}^{\prime })\rightarrow ((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
in
$(g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D703})\,:\,((X^{\prime },D^{\prime }),\unicode[STIX]{x1D706}^{\prime },f^{\prime };n^{\prime },\unicode[STIX]{x1D6FC}^{\prime })\rightarrow ((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
in
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, define the pull-back map
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, define the pull-back map
to be the pull-back along the morphism (which depends on the data
![]() $(n,\unicode[STIX]{x1D6FC})$
):
$(n,\unicode[STIX]{x1D6FC})$
):
Last, denote by
![]() $p^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}$
the map of presheaves on
$p^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}$
the map of presheaves on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
given by the pull-back along the projections
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
given by the pull-back along the projections
![]() $\mathbb{P}^{r-1}\times X\rightarrow X$
.
$\mathbb{P}^{r-1}\times X\rightarrow X$
.
The presence of
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
is the main reason why we work in
$p_{\ast }z_{\mathsf{rel}}^{i}$
is the main reason why we work in
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
rather than
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
rather than
![]() $\mathsf{MSm}^{\ast }$
. This presheaf has the information of
$\mathsf{MSm}^{\ast }$
. This presheaf has the information of
![]() $p_{\ast }z_{\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D}^{i}$
for all objects
$p_{\ast }z_{\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D}^{i}$
for all objects
![]() $((X,D),\unicode[STIX]{x1D706},f)\in \mathsf{MSm}^{\ast }$
and vector bundles
$((X,D),\unicode[STIX]{x1D706},f)\in \mathsf{MSm}^{\ast }$
and vector bundles
![]() $E\rightarrow X$
in the following sense.
$E\rightarrow X$
in the following sense.
Let us suppose
![]() $\unicode[STIX]{x1D6EC}=\{\ast \}$
for simplicity, so that
$\unicode[STIX]{x1D6EC}=\{\ast \}$
for simplicity, so that
![]() $\mathsf{MSm}^{\ast }\simeq (X,D)_{\text{Nis}}$
. Given a vector bundle
$\mathsf{MSm}^{\ast }\simeq (X,D)_{\text{Nis}}$
. Given a vector bundle
![]() $E\rightarrow X$
of rank
$E\rightarrow X$
of rank
![]() $r\geqslant 0$
, let
$r\geqslant 0$
, let
![]() $p\,:\,\mathbb{P}(E)\rightarrow X$
be the associated projective bundle
$p\,:\,\mathbb{P}(E)\rightarrow X$
be the associated projective bundle
![]() $\mathbb{P}(E):=\mathbf{Proj}(\operatorname{Sym}_{{\mathcal{O}}_{X}}E^{\vee })$
. We can consider the cycle complex
$\mathbb{P}(E):=\mathbf{Proj}(\operatorname{Sym}_{{\mathcal{O}}_{X}}E^{\vee })$
. We can consider the cycle complex
![]() $z_{\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D}^{i}\,:\,(U\xrightarrow[{}]{\acute{\text{e}}\text{t}}\mathbb{P}(E))$
$z_{\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D}^{i}\,:\,(U\xrightarrow[{}]{\acute{\text{e}}\text{t}}\mathbb{P}(E))$
![]() $\mapsto z^{i}(U|U\times _{X}D,\bullet )$
on
$\mapsto z^{i}(U|U\times _{X}D,\bullet )$
on
![]() $(\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D)_{\text{Nis}}$
and its push-forward
$(\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D)_{\text{Nis}}$
and its push-forward
![]() $p_{\ast }z_{\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D}^{i}$
to
$p_{\ast }z_{\mathbb{P}(E)|\mathbb{P}(E)\times _{X}D}^{i}$
to
![]() $(X,D)_{\text{Nis}}$
on the one hand.
$(X,D)_{\text{Nis}}$
on the one hand.
On the other hand, if we choose an open covering
![]() $X=\bigcup _{j}X_{j}$
and trivialization
$X=\bigcup _{j}X_{j}$
and trivialization
![]() $\unicode[STIX]{x1D719}_{j}\,:\,E_{|X_{j}}\cong {\mathcal{O}}_{X_{j}}^{r}$
, we get a morphism of simplicial schemes from the Čech construction
$\unicode[STIX]{x1D719}_{j}\,:\,E_{|X_{j}}\cong {\mathcal{O}}_{X_{j}}^{r}$
, we get a morphism of simplicial schemes from the Čech construction
![]() $\unicode[STIX]{x1D719}\,:\,{\check{C}}({\{X_{j}\}}_{j})\rightarrow B\text{GL}_{r}$
hence a simplicial object in
$\unicode[STIX]{x1D719}\,:\,{\check{C}}({\{X_{j}\}}_{j})\rightarrow B\text{GL}_{r}$
hence a simplicial object in
![]() $(X,D)_{\text{Nis}}/B\text{GL}_{r}$
(here, we give
$(X,D)_{\text{Nis}}/B\text{GL}_{r}$
(here, we give
![]() $X_{j}$
the divisor
$X_{j}$
the divisor
![]() $D_{j}:=D\times _{X}X_{j}$
). Therefore we can consider the restriction of
$D_{j}:=D\times _{X}X_{j}$
). Therefore we can consider the restriction of
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
to
$p_{\ast }z_{\mathsf{rel}}^{i}$
to
![]() ${\check{C}}(\{{X_{j}\}}_{j})_{\text{Nis}}$
.
${\check{C}}(\{{X_{j}\}}_{j})_{\text{Nis}}$
.
One verifies that these two presheaves are canonically isomorphic on
![]() ${\check{C}}(\{{X_{j}\}}_{j})_{\text{Nis}}$
.
${\check{C}}(\{{X_{j}\}}_{j})_{\text{Nis}}$
.
Remark 1.8. The following nonmodulus version
with the same “presheaf” structure as
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
, plays a minor role later on. Note that since we are not assuming the smoothness of
$p_{\ast }z_{\mathsf{rel}}^{i}$
, plays a minor role later on. Note that since we are not assuming the smoothness of
![]() $X$
along
$X$
along
![]() $D$
for objects of
$D$
for objects of
![]() $\mathsf{MSm}$
, it is difficult to make
$\mathsf{MSm}$
, it is difficult to make
![]() $p_{\ast }z^{i}$
functorial in a sensible way. However, this does not pose a real problem because
$p_{\ast }z^{i}$
functorial in a sensible way. However, this does not pose a real problem because
![]() $p_{\ast }z^{i}$
is only used as a conceptual aid in some constructions and can be avoided if one is willing to write down all the raw data instead.
$p_{\ast }z^{i}$
is only used as a conceptual aid in some constructions and can be avoided if one is willing to write down all the raw data instead.
1.2 Line bundles and codimension
 $1$
cycles
$1$
cycles
We know that codimension
![]() $1$
cycles are closely related to line bundles. The following version of this relationship is repeatedly used in this article. Below, we adopt the convention
$1$
cycles are closely related to line bundles. The following version of this relationship is repeatedly used in this article. Below, we adopt the convention
![]() $\Box ^{n}:=(\mathbb{P}^{1}\setminus \{\infty \})^{n}=\text{Spec}(k[t_{1},\ldots ,t_{n}])$
rather than
$\Box ^{n}:=(\mathbb{P}^{1}\setminus \{\infty \})^{n}=\text{Spec}(k[t_{1},\ldots ,t_{n}])$
rather than
![]() $(\mathbb{P}^{1}\setminus \{1\})^{n}$
used in [Reference Binda and SaitoBS17].
$(\mathbb{P}^{1}\setminus \{1\})^{n}$
used in [Reference Binda and SaitoBS17].
Let
![]() $X_{\bullet }$
be a semi-simplicial scheme with flat face maps (so that cycles and nonzero divisors can always be pulled back). Let
$X_{\bullet }$
be a semi-simplicial scheme with flat face maps (so that cycles and nonzero divisors can always be pulled back). Let
![]() $L$
be a line bundle on it, that is, the data of line bundles
$L$
be a line bundle on it, that is, the data of line bundles
![]() $L_{n}$
on
$L_{n}$
on
![]() $X_{n}$
for
$X_{n}$
for
![]() $n\geqslant 0$
and isomorphisms
$n\geqslant 0$
and isomorphisms
![]() $d_{i}^{\ast }L_{n-1}\cong L_{n}$
for face maps
$d_{i}^{\ast }L_{n-1}\cong L_{n}$
for face maps
![]() $d_{i}\,:\,X_{n}\rightarrow X_{n-1}$
, compatible with each other in an obvious sense.
$d_{i}\,:\,X_{n}\rightarrow X_{n-1}$
, compatible with each other in an obvious sense.
Suppose we are given a section
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}(X_{0},L_{0})$
which is everywhere a nonzero divisor. We are going to define sections
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}(X_{0},L_{0})$
which is everywhere a nonzero divisor. We are going to define sections
on
![]() $X_{n}\times \Box ^{n}$
which are nonzero divisors everywhere.
$X_{n}\times \Box ^{n}$
which are nonzero divisors everywhere.
Let us denote by
![]() $v_{k}^{[n]}\,:\,[0]\rightarrow [n]$
the inclusion of the
$v_{k}^{[n]}\,:\,[0]\rightarrow [n]$
the inclusion of the
![]() $k$
th vertex. Note that the groups
$k$
th vertex. Note that the groups
![]() $\unicode[STIX]{x1D6E4}(X_{m},L_{m})\,\otimes _{k}\,k[t_{1},\ldots ,t_{n}]$
are semi-cosimplicial in
$\unicode[STIX]{x1D6E4}(X_{m},L_{m})\,\otimes _{k}\,k[t_{1},\ldots ,t_{n}]$
are semi-cosimplicial in
![]() $m$
and cubical in
$m$
and cubical in
![]() $n$
. In particular, we have sections
$n$
. In particular, we have sections
![]() $(v_{k}^{[n]})_{\ast }\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}(X_{n},L_{n}).$
We define
$(v_{k}^{[n]})_{\ast }\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}(X_{n},L_{n}).$
We define
![]() $F\text{}_{n}^{(\unicode[STIX]{x1D70E})}$
by the formula
$F\text{}_{n}^{(\unicode[STIX]{x1D70E})}$
by the formula
where
![]() $t_{0}=1$
by convention. Of course, it is the map corresponding to the composite of a map
$t_{0}=1$
by convention. Of course, it is the map corresponding to the composite of a map
![]() $\displaystyle \Box ^{n}\rightarrow \unicode[STIX]{x1D6E5}^{n}$
from the
$\displaystyle \Box ^{n}\rightarrow \unicode[STIX]{x1D6E5}^{n}$
from the
![]() $n$
-cube to the (algebraic)
$n$
-cube to the (algebraic)
![]() $n$
-simplex, followed by the affine map
$n$
-simplex, followed by the affine map
![]() $\unicode[STIX]{x1D6E5}^{n}\rightarrow \unicode[STIX]{x1D6E4}(X_{n},L_{n})$
sending the
$\unicode[STIX]{x1D6E5}^{n}\rightarrow \unicode[STIX]{x1D6E4}(X_{n},L_{n})$
sending the
![]() $k$
th vertex to
$k$
th vertex to
![]() $(v_{k}^{[n]})_{\ast }\unicode[STIX]{x1D70E}$
. Footnote
1
$(v_{k}^{[n]})_{\ast }\unicode[STIX]{x1D70E}$
. Footnote
1
Recall that for
![]() $1\leqslant j\leqslant n$
and
$1\leqslant j\leqslant n$
and
![]() $\unicode[STIX]{x1D716}=0,1$
, the map
$\unicode[STIX]{x1D716}=0,1$
, the map
![]() $\unicode[STIX]{x2202}_{j,\unicode[STIX]{x1D716}}\,:\,\Box ^{n-1}\rightarrow \Box ^{n}$
is the embedding of the face
$\unicode[STIX]{x2202}_{j,\unicode[STIX]{x1D716}}\,:\,\Box ^{n-1}\rightarrow \Box ^{n}$
is the embedding of the face
![]() $\{t_{j}=\unicode[STIX]{x1D716}\}$
:
$\{t_{j}=\unicode[STIX]{x1D716}\}$
:
![]() $(t_{1},\ldots ,t_{n-1})\mapsto (t_{1},\ldots ,t_{j-1},\unicode[STIX]{x1D716},t_{j},\ldots ,t_{n-1})$
. Degenerate elements of a cubical set mean elements obtained by pull-back along degeneracy maps
$(t_{1},\ldots ,t_{n-1})\mapsto (t_{1},\ldots ,t_{j-1},\unicode[STIX]{x1D716},t_{j},\ldots ,t_{n-1})$
. Degenerate elements of a cubical set mean elements obtained by pull-back along degeneracy maps
![]() $\Box ^{n}\rightarrow \Box ^{n-1}$
. Also for
$\Box ^{n}\rightarrow \Box ^{n-1}$
. Also for
![]() $0\leqslant i\leqslant n$
, denote by
$0\leqslant i\leqslant n$
, denote by
![]() $d_{i}\,:\,[n-1]\rightarrow [n]$
the
$d_{i}\,:\,[n-1]\rightarrow [n]$
the
![]() $i$
th face of
$i$
th face of
![]() $[n]$
. It is routine to check the following relations.
$[n]$
. It is routine to check the following relations.
Lemma 1.9. We have equalities in
![]() $\unicode[STIX]{x1D6E4}(X_{n},L_{n})\,\otimes _{k}\,k[t_{1},\ldots ,t_{n-1}]$
:
$\unicode[STIX]{x1D6E4}(X_{n},L_{n})\,\otimes _{k}\,k[t_{1},\ldots ,t_{n-1}]$
:
Also, the functions
![]() $\unicode[STIX]{x2202}_{j,1}^{\ast }F\text{}_{n}^{(\unicode[STIX]{x1D70E})}$
are degenerate for
$\unicode[STIX]{x2202}_{j,1}^{\ast }F\text{}_{n}^{(\unicode[STIX]{x1D70E})}$
are degenerate for
![]() $1<j\leqslant n$
.
$1<j\leqslant n$
.
Let
![]() $z^{1}(-,\bullet )$
be Bloch’s codimension
$z^{1}(-,\bullet )$
be Bloch’s codimension
![]() $1$
cycle complex, which is a presheaf on the category of schemes and flat morphisms. For a scheme
$1$
cycle complex, which is a presheaf on the category of schemes and flat morphisms. For a scheme
![]() $X$
, let
$X$
, let
![]() $\mathbb{Z}[X]$
be the additive presheaf generated by the presheaf of sets represented by
$\mathbb{Z}[X]$
be the additive presheaf generated by the presheaf of sets represented by
![]() $X$
. Lemma 1.9 implies that the set of cycles
$X$
. Lemma 1.9 implies that the set of cycles
![]() $\{\unicode[STIX]{x1D6E4}\text{}_{n}^{(\unicode[STIX]{x1D70E})}\}_{n}:=\{\text{div}(F\text{}_{n}^{(\unicode[STIX]{x1D70E})})\}_{n}$
determines a map of presheaves of complexes
$\{\unicode[STIX]{x1D6E4}\text{}_{n}^{(\unicode[STIX]{x1D70E})}\}_{n}:=\{\text{div}(F\text{}_{n}^{(\unicode[STIX]{x1D70E})})\}_{n}$
determines a map of presheaves of complexes
on the small flat site over the semi-simplicial scheme
![]() $X_{\bullet }$
.
$X_{\bullet }$
.
Let
![]() $\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6E4}(X_{0},L_{0})$
be another nowhere zero divisor. We set
$\unicode[STIX]{x1D70E}^{\prime }\in \unicode[STIX]{x1D6E4}(X_{0},L_{0})$
be another nowhere zero divisor. We set
The cycles
![]() $\unicode[STIX]{x1D6E4}\text{}_{n}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}:=\text{div}(F\text{}_{n}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })})$
will serve as a homotopy of
$\unicode[STIX]{x1D6E4}\text{}_{n}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}:=\text{div}(F\text{}_{n}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })})$
will serve as a homotopy of
![]() $\unicode[STIX]{x1D6E4}\text{}^{(\unicode[STIX]{x1D70E})}$
and
$\unicode[STIX]{x1D6E4}\text{}^{(\unicode[STIX]{x1D70E})}$
and
![]() $\unicode[STIX]{x1D6E4}\text{}^{(\unicode[STIX]{x1D70E}^{\prime })}$
.
$\unicode[STIX]{x1D6E4}\text{}^{(\unicode[STIX]{x1D70E}^{\prime })}$
.
1.2.1 Variant
Occasionally our line bundle
![]() $L$
will be given as the difference
$L$
will be given as the difference
![]() $L=L^{+}\otimes (L^{-})^{\vee }$
of two line bundles, each equipped with a nowhere zero divisor
$L=L^{+}\otimes (L^{-})^{\vee }$
of two line bundles, each equipped with a nowhere zero divisor
![]() $\unicode[STIX]{x1D70E}^{\pm }\in \unicode[STIX]{x1D6E4}(X_{0},L_{0}^{\pm })$
in degree
$\unicode[STIX]{x1D70E}^{\pm }\in \unicode[STIX]{x1D6E4}(X_{0},L_{0}^{\pm })$
in degree
![]() $0$
. The construction of
$0$
. The construction of
![]() $\unicode[STIX]{x1D6E4}\text{}^{(\unicode[STIX]{x1D70E})}$
makes sense for the ratio
$\unicode[STIX]{x1D6E4}\text{}^{(\unicode[STIX]{x1D70E})}$
makes sense for the ratio
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}^{+}/\unicode[STIX]{x1D70E}^{-}$
. In this case
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}^{+}/\unicode[STIX]{x1D70E}^{-}$
. In this case
![]() $F\text{}_{n}^{(\unicode[STIX]{x1D70E})}$
is the ratio of an element in
$F\text{}_{n}^{(\unicode[STIX]{x1D70E})}$
is the ratio of an element in
![]() $\unicode[STIX]{x1D6E4}(X_{n},L_{n}^{+}\otimes (L_{n}^{-})^{\otimes n})\,\otimes _{k}\,k[t_{1},\ldots ,t_{n}]$
and an element in
$\unicode[STIX]{x1D6E4}(X_{n},L_{n}^{+}\otimes (L_{n}^{-})^{\otimes n})\,\otimes _{k}\,k[t_{1},\ldots ,t_{n}]$
and an element in
![]() $\unicode[STIX]{x1D6E4}(X_{n},(L_{n}^{-})^{\otimes n+1})$
(for example,
$\unicode[STIX]{x1D6E4}(X_{n},(L_{n}^{-})^{\otimes n+1})$
(for example,
![]() $F_{0}^{(\unicode[STIX]{x1D70E})}=\unicode[STIX]{x1D70E}^{+}/\unicode[STIX]{x1D70E}^{-}$
is the ratio of an element in
$F_{0}^{(\unicode[STIX]{x1D70E})}=\unicode[STIX]{x1D70E}^{+}/\unicode[STIX]{x1D70E}^{-}$
is the ratio of an element in
![]() $\unicode[STIX]{x1D6E4}(X_{0},L_{0}^{+})$
and one in
$\unicode[STIX]{x1D6E4}(X_{0},L_{0}^{+})$
and one in
![]() $\unicode[STIX]{x1D6E4}(X_{0},L_{0}^{-})$
).
$\unicode[STIX]{x1D6E4}(X_{0},L_{0}^{-})$
).
Also if a second presentation
![]() $L=L^{\prime +}\otimes (L^{\prime -})^{\vee }$
and nonzero divisors
$L=L^{\prime +}\otimes (L^{\prime -})^{\vee }$
and nonzero divisors
![]() $\unicode[STIX]{x1D70E}^{\prime \pm }\in \unicode[STIX]{x1D6E4}(X_{0},L_{0}^{\prime \pm })$
are given, the construction of the homotopy
$\unicode[STIX]{x1D70E}^{\prime \pm }\in \unicode[STIX]{x1D6E4}(X_{0},L_{0}^{\prime \pm })$
are given, the construction of the homotopy
![]() $F\text{}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}$
makes sense to give
$F\text{}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}$
makes sense to give
![]() $F\text{}_{n}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}$
as the ratio of an element in
$F\text{}_{n}^{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime })}$
as the ratio of an element in
![]() $\unicode[STIX]{x1D6E4}(X_{n},L\otimes (L^{-})^{\otimes n+1}\otimes (L^{\prime -})^{\otimes n+1})\otimes _{k}k[t_{1},\ldots ,t_{n+1}]$
and an element in
$\unicode[STIX]{x1D6E4}(X_{n},L\otimes (L^{-})^{\otimes n+1}\otimes (L^{\prime -})^{\otimes n+1})\otimes _{k}k[t_{1},\ldots ,t_{n+1}]$
and an element in
![]() $\unicode[STIX]{x1D6E4}(X_{n},(L^{-})^{\otimes n+1}\otimes (L^{\prime -})^{\otimes n+1})$
.
$\unicode[STIX]{x1D6E4}(X_{n},(L^{-})^{\otimes n+1}\otimes (L^{\prime -})^{\otimes n+1})$
.
We will need the next complete intersection criterion. For the proof, the reader is referred to Lemma B.3.
Lemma 1.10. Let
![]() $L^{(1)\pm },\ldots ,L^{(i)\pm }$
be
$L^{(1)\pm },\ldots ,L^{(i)\pm }$
be
![]() $2i$
line bundles on
$2i$
line bundles on
![]() $X_{\bullet }$
equipped with sections
$X_{\bullet }$
equipped with sections
![]() $\unicode[STIX]{x1D70E}_{a}^{\pm }$
of
$\unicode[STIX]{x1D70E}_{a}^{\pm }$
of
![]() $L_{0}^{(a)\pm }$
which are nonzero divisors (
$L_{0}^{(a)\pm }$
which are nonzero divisors (
![]() $1\leqslant a\leqslant i$
). Suppose the sequence of
$1\leqslant a\leqslant i$
). Suppose the sequence of
![]() $i$
sections
$i$
sections
is a regular sequence for every
![]() $n\geqslant 0$
and every choice of
$n\geqslant 0$
and every choice of
![]() $0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant n$
and signs
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant n$
and signs
![]() $\pm$
. Then the cup product
$\pm$
. Then the cup product
is well defined.
Here, the cup product is defined by the concrete formulas in Appendix B.2. It is said to be well defined if all the intersection products appearing in the expression are well defined.
1.3 The projective bundle formula
Now we can state and prove the main result of this section:
Theorem 1.11. (Projective bundle formula)
For every
![]() $i\geqslant 0$
, we have a canonical isomorphism in the Nisnevich-local derived category
$i\geqslant 0$
, we have a canonical isomorphism in the Nisnevich-local derived category
![]() $D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
:
$D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
:
First, we have to construct the maps. The following is a consequence of the Friedlander–Lawson moving lemma [Reference Friedlander and LawsonFL98, Theorem 3.1]. In the lemma and onwards, the superscript
![]() $(-)^{\circ }$
will be used to indicate that some moving procedure is involved.
$(-)^{\circ }$
will be used to indicate that some moving procedure is involved.
Lemma 1.12. Let
![]() $k$
be a field and
$k$
be a field and
![]() $e\geqslant 1$
be an integer. Let
$e\geqslant 1$
be an integer. Let
![]() $\mathbb{P}^{m}$
be the
$\mathbb{P}^{m}$
be the
![]() $m$
-dimensional projective space over
$m$
-dimensional projective space over
![]() $k$
(
$k$
(
![]() $m\geqslant 0$
). Then there is a codimension
$m\geqslant 0$
). Then there is a codimension
![]() $1$
cycle
$1$
cycle
![]() $H^{\circ }$
on
$H^{\circ }$
on
![]() $\mathbb{P}^{m}$
representing
$\mathbb{P}^{m}$
representing
![]() ${\mathcal{O}}(1)$
such that for every effective cycle
${\mathcal{O}}(1)$
such that for every effective cycle
![]() $Z\subset \mathbb{P}_{\bar{k}}^{m}$
of positive dimension and of degree
$Z\subset \mathbb{P}_{\bar{k}}^{m}$
of positive dimension and of degree
![]() ${\leqslant}e$
(over
${\leqslant}e$
(over
![]() $\bar{k}$
), the intersection of
$\bar{k}$
), the intersection of
![]() $Z$
and
$Z$
and
![]() $H_{\bar{k}}^{\circ }\text{ in }\mathbb{P}_{\bar{k}}^{m}$
is proper.
$H_{\bar{k}}^{\circ }\text{ in }\mathbb{P}_{\bar{k}}^{m}$
is proper.
Let
![]() $H\text{}^{(1)\circ }:=\text{div}(\unicode[STIX]{x1D70E}_{1})\subset \mathbb{P}^{r-1}$
be any hyperplane (i.e.,
$H\text{}^{(1)\circ }:=\text{div}(\unicode[STIX]{x1D70E}_{1})\subset \mathbb{P}^{r-1}$
be any hyperplane (i.e.,
![]() $\unicode[STIX]{x1D70E}_{1}\in {\mathcal{O}}(1)$
). Applying Lemma with
$\unicode[STIX]{x1D70E}_{1}\in {\mathcal{O}}(1)$
). Applying Lemma with
![]() $e=1$
gives a codimension
$e=1$
gives a codimension
![]() $1$
cycle
$1$
cycle
![]() $H\text{}^{(2)\circ }$
on
$H\text{}^{(2)\circ }$
on
![]() $\mathbb{P}^{r-1}$
which intersect every linear translate of
$\mathbb{P}^{r-1}$
which intersect every linear translate of
![]() $H\text{}^{(1)\circ }$
properly.
$H\text{}^{(1)\circ }$
properly.
![]() $H\text{}^{(2)\circ }$
is written as the difference of the divisor of a section
$H\text{}^{(2)\circ }$
is written as the difference of the divisor of a section
![]() $\unicode[STIX]{x1D70E}_{2}^{+}\in {\mathcal{O}}(d+1)$
of some degree
$\unicode[STIX]{x1D70E}_{2}^{+}\in {\mathcal{O}}(d+1)$
of some degree
![]() $d>0$
and that of
$d>0$
and that of
![]() $\unicode[STIX]{x1D70E}_{2}^{-}\in {\mathcal{O}}(d)$
. (Of course, any sections with
$\unicode[STIX]{x1D70E}_{2}^{-}\in {\mathcal{O}}(d)$
. (Of course, any sections with
![]() $d\geqslant 2$
work for this first step without appealing to Lemma.) Next, apply Lemma 1.12 with
$d\geqslant 2$
work for this first step without appealing to Lemma.) Next, apply Lemma 1.12 with
![]() $e=d+1$
and find sections
$e=d+1$
and find sections
![]() $\unicode[STIX]{x1D70E}_{3}^{+}\in {\mathcal{O}}(d^{\prime }+1)$
,
$\unicode[STIX]{x1D70E}_{3}^{+}\in {\mathcal{O}}(d^{\prime }+1)$
,
![]() $\unicode[STIX]{x1D70E}_{3}^{-}\in {\mathcal{O}}(d^{\prime })$
of some large degrees so that the cycle
$\unicode[STIX]{x1D70E}_{3}^{-}\in {\mathcal{O}}(d^{\prime })$
of some large degrees so that the cycle
![]() $H\text{}^{(3)\circ }:=\text{div}(\unicode[STIX]{x1D70E}_{3}^{+}/\unicode[STIX]{x1D70E}_{3}^{-})$
satisfies the condition that for every
$H\text{}^{(3)\circ }:=\text{div}(\unicode[STIX]{x1D70E}_{3}^{+}/\unicode[STIX]{x1D70E}_{3}^{-})$
satisfies the condition that for every
![]() $(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\in \text{GL}_{r}(\bar{k})^{2}$
the following set has codimension
$(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\in \text{GL}_{r}(\bar{k})^{2}$
the following set has codimension
![]() $3$
in
$3$
in
![]() $\mathbb{P}_{\bar{k}}^{r-1}$
(the symbol
$\mathbb{P}_{\bar{k}}^{r-1}$
(the symbol
![]() $|-|$
denotes the support of a cycle):
$|-|$
denotes the support of a cycle):
This works because the intersection of the first two factors (with the reduced structure) has been assured to have codimension 2 and has degree
![]() ${\leqslant}1\cdot (d+1)$
. Next apply Lemma 1.12 with
${\leqslant}1\cdot (d+1)$
. Next apply Lemma 1.12 with
![]() $e=(d+1)(d^{\prime }+1)$
to get
$e=(d+1)(d^{\prime }+1)$
to get
![]() $H\text{}^{(4)\circ }=\text{div}(\unicode[STIX]{x1D70E}_{4}^{+}/\unicode[STIX]{x1D70E}_{4}^{-})$
and so on.
$H\text{}^{(4)\circ }=\text{div}(\unicode[STIX]{x1D70E}_{4}^{+}/\unicode[STIX]{x1D70E}_{4}^{-})$
and so on.
In the end, we get codimension
![]() $1$
cycles
$1$
cycles
![]() $H\text{}^{(a)\circ }=\text{div}(\unicode[STIX]{x1D70E}_{a}^{+}/\unicode[STIX]{x1D70E}_{a}^{-})$
on
$H\text{}^{(a)\circ }=\text{div}(\unicode[STIX]{x1D70E}_{a}^{+}/\unicode[STIX]{x1D70E}_{a}^{-})$
on
![]() $\mathbb{P}^{r-1}$
(
$\mathbb{P}^{r-1}$
(
![]() $1\leqslant a\leqslant r-1$
) with the property that for every
$1\leqslant a\leqslant r-1$
) with the property that for every
![]() $(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r-1})\in \text{GL}_{r}(\bar{k})^{r-1}$
the intersection
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r-1})\in \text{GL}_{r}(\bar{k})^{r-1}$
the intersection
is zero-dimensional. In other words, the sequence
![]() $[\unicode[STIX]{x1D6FC}_{1}]^{\ast }\unicode[STIX]{x1D70E}_{1}^{\pm },\ldots ,[\unicode[STIX]{x1D6FC}_{r-1}]^{\ast }\unicode[STIX]{x1D70E}_{r-1}^{\pm }$
is a regular sequence for every possible choice of signs
$[\unicode[STIX]{x1D6FC}_{1}]^{\ast }\unicode[STIX]{x1D70E}_{1}^{\pm },\ldots ,[\unicode[STIX]{x1D6FC}_{r-1}]^{\ast }\unicode[STIX]{x1D70E}_{r-1}^{\pm }$
is a regular sequence for every possible choice of signs
![]() $\pm$
. Applying the procedure in Section 1.2 to these data, we get cycles which we denote by
$\pm$
. Applying the procedure in Section 1.2 to these data, we get cycles which we denote by
![]() $\unicode[STIX]{x1D6E4}\text{}_{n}^{(a)\circ }$
(
$\unicode[STIX]{x1D6E4}\text{}_{n}^{(a)\circ }$
(
![]() $1\leqslant a\leqslant r-1$
):
$1\leqslant a\leqslant r-1$
):
Now, let us note that giving a section
![]() $((X,D),\unicode[STIX]{x1D706},f)\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}B_{n}\text{GL}_{r}$
of
$((X,D),\unicode[STIX]{x1D706},f)\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}B_{n}\text{GL}_{r}$
of
![]() $B\text{GL}_{r}$
in degree
$B\text{GL}_{r}$
in degree
![]() $n$
is equivalent to giving a map
$n$
is equivalent to giving a map
![]() $((X,D),\unicode[STIX]{x1D706},f)\times \unicode[STIX]{x1D6E5}^{n}\rightarrow B\text{GL}_{r}$
of simplicial presheaves on
$((X,D),\unicode[STIX]{x1D706},f)\times \unicode[STIX]{x1D6E5}^{n}\rightarrow B\text{GL}_{r}$
of simplicial presheaves on
![]() $\mathsf{MSm}^{\ast }$
(here,
$\mathsf{MSm}^{\ast }$
(here,
![]() $\unicode[STIX]{x1D6E5}^{n}$
is a simplicial set, not a scheme). This motivates the following:
$\unicode[STIX]{x1D6E5}^{n}$
is a simplicial set, not a scheme). This motivates the following:
Definition 1.13. Let
![]() $\unicode[STIX]{x1D6E5}$
be the simplicial presheaf on
$\unicode[STIX]{x1D6E5}$
be the simplicial presheaf on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
given by
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
given by
on objects and
![]() $(g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D703})\mapsto \unicode[STIX]{x1D703}$
on morphisms.
$(g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D703})\mapsto \unicode[STIX]{x1D703}$
on morphisms.
The projection
![]() $\unicode[STIX]{x1D6E5}\rightarrow \ast$
to the singleton is a sectionwise weak equivalence of simplicial presheaves on
$\unicode[STIX]{x1D6E5}\rightarrow \ast$
to the singleton is a sectionwise weak equivalence of simplicial presheaves on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
because
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
because
![]() $\unicode[STIX]{x1D6E5}^{n}$
is contractible.
$\unicode[STIX]{x1D6E5}^{n}$
is contractible.
Definition 1.14. For every object
![]() $\mathfrak{X}:=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, a simplex
$\mathfrak{X}:=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
, a simplex
![]() $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
and an index
$\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
and an index
![]() $a\in \{1,\ldots ,r-1\}$
, denote by
$a\in \{1,\ldots ,r-1\}$
, denote by
the pull-back of
![]() $\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\circ }$
by the map
$\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\circ }$
by the map
![]() $\{\mathbb{P}(E\text{GL}_{r})(\unicode[STIX]{x1D703})\times \text{id}_{\Box ^{m}}\}\circ \{\text{id}_{\mathbb{P}^{r-1}}\times \unicode[STIX]{x1D6FC}\times \text{id}_{\Box ^{m}}\}$
:
$\{\mathbb{P}(E\text{GL}_{r})(\unicode[STIX]{x1D703})\times \text{id}_{\Box ^{m}}\}\circ \{\text{id}_{\mathbb{P}^{r-1}}\times \unicode[STIX]{x1D6FC}\times \text{id}_{\Box ^{m}}\}$
:
Using them, we define a map of complexes
as follows: On an object
![]() $\mathfrak{X}$
as above and in degree
$\mathfrak{X}$
as above and in degree
![]() $m$
, we must give a map of presheaves
$m$
, we must give a map of presheaves
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}_{m}^{n}\rightarrow p_{\ast }z^{1}(\mathfrak{X},m)=z^{1}(\mathbb{P}^{r-1}\times X,m)$
. We do this by mapping
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}_{m}^{n}\rightarrow p_{\ast }z^{1}(\mathfrak{X},m)=z^{1}(\mathbb{P}^{r-1}\times X,m)$
. We do this by mapping
![]() $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
to
$\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
to
![]() $\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})$
.
$\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})$
.
Of course, we could have pulled back the function
![]() $F\text{}_{m}^{(\unicode[STIX]{x1D70E}_{a}^{+}/\unicode[STIX]{x1D70E}_{a}^{-})}$
to define a function
$F\text{}_{m}^{(\unicode[STIX]{x1D70E}_{a}^{+}/\unicode[STIX]{x1D70E}_{a}^{-})}$
to define a function
![]() $F\text{}_{m}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})$
(a ratio of nowhere zero divisors by direct inspection) and set
$F\text{}_{m}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})$
(a ratio of nowhere zero divisors by direct inspection) and set
![]() $\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})$
as its divisor. Both give the same cycle.
$\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})$
as its divisor. Both give the same cycle.
The cup product below is well defined for every
![]() $1\leqslant j\leqslant r-1$
:
$1\leqslant j\leqslant r-1$
:
thanks to proper intersection (2) and Lemma 1.10 applied on each object of
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
. We tensor both sides with
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
. We tensor both sides with
![]() $z_{\mathsf{rel}}^{i-j}$
and apply the intersection product in the Nisnevich-local derived category (Appendix B.1):
$z_{\mathsf{rel}}^{i-j}$
and apply the intersection product in the Nisnevich-local derived category (Appendix B.1):
Composed with the inverse of the quasi-isomorphism
![]() $z_{\mathsf{rel}}^{i-j}\otimes \unicode[STIX]{x1D6E5}\xrightarrow[{}]{{\sim}}z_{\mathsf{rel}}^{i-j}$
, it gives us the maps which we call
$z_{\mathsf{rel}}^{i-j}\otimes \unicode[STIX]{x1D6E5}\xrightarrow[{}]{{\sim}}z_{\mathsf{rel}}^{i-j}$
, it gives us the maps which we call
![]() $p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}$
:
$p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}$
:
Proof of Theorem 1.11.
We now claim that the map
![]() $\sum _{j=0}^{r-1}(p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j})$
is an isomorphism in
$\sum _{j=0}^{r-1}(p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j})$
is an isomorphism in
![]() $D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
. For this purpose, we may work locally. We consider an object
$D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
. For this purpose, we may work locally. We consider an object
![]() $\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
and assume
$\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
and assume
![]() $X$
is henselian. Consider the weak equivalence
$X$
is henselian. Consider the weak equivalence
![]() $z_{\mathsf{rel}}^{i-j}(\mathfrak{X},\bullet ){\hookrightarrow}z_{\mathsf{rel}}^{i-j}(\mathfrak{X},\bullet )\otimes \unicode[STIX]{x1D6E5}^{n}$
corresponding to the inclusion of the
$z_{\mathsf{rel}}^{i-j}(\mathfrak{X},\bullet ){\hookrightarrow}z_{\mathsf{rel}}^{i-j}(\mathfrak{X},\bullet )\otimes \unicode[STIX]{x1D6E5}^{n}$
corresponding to the inclusion of the
![]() $0$
th vertex
$0$
th vertex
![]() $\ast {\hookrightarrow}\unicode[STIX]{x1D6E5}^{n}$
. One computes the composition of it with
$\ast {\hookrightarrow}\unicode[STIX]{x1D6E5}^{n}$
. One computes the composition of it with
![]() $p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}$
as
$p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}$
as
![]() $V\mapsto (H\text{}^{(1)\circ }\,\cdot \,\ldots \,\cdot \,H\text{}^{(j)\circ })\times V$
which is well defined for all
$V\mapsto (H\text{}^{(1)\circ }\,\cdot \,\ldots \,\cdot \,H\text{}^{(j)\circ })\times V$
which is well defined for all
![]() $V$
. This gives maps
$V$
. This gives maps
![]() $\text{CH}^{i-j}(X|D,m)$
$\text{CH}^{i-j}(X|D,m)$
![]() $\rightarrow$
$\rightarrow$
![]() $\text{CH}^{i}(\mathbb{P}^{r-1}\times X|\mathbb{P}^{r-1}\times D,m)$
on homology.
$\text{CH}^{i}(\mathbb{P}^{r-1}\times X|\mathbb{P}^{r-1}\times D,m)$
on homology.
Projective bundle formula for the higher Chow groups with modulus is known by Krishna, Levine and Park [Reference Krishna and LevineKL08, Theorem 5.6], [Reference Krishna and ParkKP14, Theorem 4.6]. For pairs
![]() $(X,D)$
with
$(X,D)$
with
![]() $X$
henselian, their and our maps
$X$
henselian, their and our maps
![]() $\text{CH}^{i-j}(X|D,m)$
$\text{CH}^{i-j}(X|D,m)$
![]() $\rightarrow$
$\rightarrow$
![]() $\text{CH}^{i}(\mathbb{P}^{r-1}\times X|\mathbb{P}^{r-1}\times D,m)$
coincide, because both are computed as the classical intersection product once we are reduced to the proper intersection case. This completes the proof of Theorem 1.11.
$\text{CH}^{i}(\mathbb{P}^{r-1}\times X|\mathbb{P}^{r-1}\times D,m)$
coincide, because both are computed as the classical intersection product once we are reduced to the proper intersection case. This completes the proof of Theorem 1.11.
2 The universal Chern classes
A key ingredient of Chern classes in Bloch’s higher Chow groups is the
![]() $r$
th power
$r$
th power
of the class
![]() $\unicode[STIX]{x1D709}:=[{\mathcal{O}}(1)]$
on the simplicial scheme
$\unicode[STIX]{x1D709}:=[{\mathcal{O}}(1)]$
on the simplicial scheme
![]() $\mathbb{P}(E\text{GL}_{r})$
. By local homotopy theory, it corresponds to a map
$\mathbb{P}(E\text{GL}_{r})$
. By local homotopy theory, it corresponds to a map
![]() $\unicode[STIX]{x1D709}^{r}\,:\,\mathbb{Z}\rightarrow p_{\ast }z^{r}$
in
$\unicode[STIX]{x1D709}^{r}\,:\,\mathbb{Z}\rightarrow p_{\ast }z^{r}$
in
![]() $D(\mathsf{Sm}^{\ast }/B\text{GL}_{r})$
, where
$D(\mathsf{Sm}^{\ast }/B\text{GL}_{r})$
, where
![]() $\mathsf{Sm}^{\ast }$
is the nonmodulus version of
$\mathsf{Sm}^{\ast }$
is the nonmodulus version of
![]() $\mathsf{MSm}^{\ast }$
. In the first half of this section (Sections 2.1–2.4), we construct a map
$\mathsf{MSm}^{\ast }$
. In the first half of this section (Sections 2.1–2.4), we construct a map
Here
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}\subset B\text{GL}_{r}$
is a subpresheaf called the relative Volodin space, which is known to represent the relative
$\boldsymbol{X}_{r}^{\mathsf{rel}}\subset B\text{GL}_{r}$
is a subpresheaf called the relative Volodin space, which is known to represent the relative
![]() $K$
-theory upon
$K$
-theory upon
![]() $\mathbb{Z}$
-completion (Sections 2.3, 2.6). This map is a lifting of the classical
$\mathbb{Z}$
-completion (Sections 2.3, 2.6). This map is a lifting of the classical
![]() $\unicode[STIX]{x1D709}^{r}$
in the following sense. In the underlying datum
$\unicode[STIX]{x1D709}^{r}$
in the following sense. In the underlying datum
![]() $F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{MSm}$
, let
$F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{MSm}$
, let
![]() $\unicode[STIX]{x1D6EC}_{\emptyset }\subset \unicode[STIX]{x1D6EC}$
be the full subcategory of objects
$\unicode[STIX]{x1D6EC}_{\emptyset }\subset \unicode[STIX]{x1D6EC}$
be the full subcategory of objects
![]() $\unicode[STIX]{x1D706}$
such that
$\unicode[STIX]{x1D706}$
such that
![]() $D_{\unicode[STIX]{x1D706}}=\emptyset$
. Then
$D_{\unicode[STIX]{x1D706}}=\emptyset$
. Then
![]() $F$
restricts to
$F$
restricts to
![]() $F_{\emptyset }\,:\,\unicode[STIX]{x1D6EC}_{\emptyset }\rightarrow \mathsf{Sm}$
;
$F_{\emptyset }\,:\,\unicode[STIX]{x1D6EC}_{\emptyset }\rightarrow \mathsf{Sm}$
;
![]() $\unicode[STIX]{x1D706}\mapsto X_{\unicode[STIX]{x1D706}}$
, so we define
$\unicode[STIX]{x1D706}\mapsto X_{\unicode[STIX]{x1D706}}$
, so we define
![]() $\mathsf{Sm}^{\ast }:=\mathsf{Sm}/F_{\emptyset }$
. If one remembers (or interprets) how to construct the classical
$\mathsf{Sm}^{\ast }:=\mathsf{Sm}/F_{\emptyset }$
. If one remembers (or interprets) how to construct the classical
![]() $\unicode[STIX]{x1D709}^{r}$
correctly, it turns out that our
$\unicode[STIX]{x1D709}^{r}$
correctly, it turns out that our
![]() $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
lifts
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
lifts
![]() $\unicode[STIX]{x1D709}^{r}$
via the restriction map
$\unicode[STIX]{x1D709}^{r}$
via the restriction map
In the latter half (Sections 2.5–2.6), we discuss the stabilization process
![]() $r\rightarrow \infty$
and
$r\rightarrow \infty$
and
![]() $\mathbb{Z}$
-completion to derive Chern class maps
$\mathbb{Z}$
-completion to derive Chern class maps
2.1 Hyperplanes
We often consider data
![]() $(\mathfrak{X},\unicode[STIX]{x1D703})$
of an object
$(\mathfrak{X},\unicode[STIX]{x1D703})$
of an object
![]() $\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
$\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
![]() $\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
and an ordered map
$\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
and an ordered map
![]() $\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
.
$\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
.
2.1.1 The standard hyperplanes
Let
![]() $T_{1},\ldots ,T_{r}\in \unicode[STIX]{x1D6E4}(\mathbb{P}^{r-1},{\mathcal{O}}(1))$
be the homogeneous coordinates on
$T_{1},\ldots ,T_{r}\in \unicode[STIX]{x1D6E4}(\mathbb{P}^{r-1},{\mathcal{O}}(1))$
be the homogeneous coordinates on
![]() $\mathbb{P}^{r-1}$
. We apply Section 1.2 to the line bundle
$\mathbb{P}^{r-1}$
. We apply Section 1.2 to the line bundle
![]() ${\mathcal{O}}(1)$
on
${\mathcal{O}}(1)$
on
![]() $\mathbb{P}(E\text{GL}_{r})$
and sections
$\mathbb{P}(E\text{GL}_{r})$
and sections
![]() $T_{a}$
for
$T_{a}$
for
![]() $a\in \{1,\ldots ,r\}$
to get functions
$a\in \{1,\ldots ,r\}$
to get functions
and their divisors
![]() $\unicode[STIX]{x1D6E4}\text{}_{n}^{(a)\ast }:=\text{div}(F\text{}_{n}^{(a)\ast })\in z^{1}(\mathbb{P}(E_{n}\text{GL}_{r}),n)$
. Here we use superscripts
$\unicode[STIX]{x1D6E4}\text{}_{n}^{(a)\ast }:=\text{div}(F\text{}_{n}^{(a)\ast })\in z^{1}(\mathbb{P}(E_{n}\text{GL}_{r}),n)$
. Here we use superscripts
![]() $(-)^{\ast }$
because they will be useful only over certain open subsets which will be indicated by the same superscripts.
$(-)^{\ast }$
because they will be useful only over certain open subsets which will be indicated by the same superscripts.
Repeat the construction of Definition 1.14 on these data to define cycles
![]() $\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\ast }(\mathfrak{X},\unicode[STIX]{x1D703})\in z^{1}(\mathbb{P}^{r-1}\times X,m)$
. They determine a map of complexes
$\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\ast }(\mathfrak{X},\unicode[STIX]{x1D703})\in z^{1}(\mathbb{P}^{r-1}\times X,m)$
. They determine a map of complexes
Remark 2.1. One may want to construct
![]() $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
as the cup product
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
as the cup product
![]() $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(r)\ast }$
:
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(r)\ast }$
:
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\rightarrow p_{\ast }z^{r}$
. But the cup product is not well defined due to the failure of proper intersection. The easiest such example would be, taking
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\rightarrow p_{\ast }z^{r}$
. But the cup product is not well defined due to the failure of proper intersection. The easiest such example would be, taking
![]() $\unicode[STIX]{x1D6EC}=\{\ast \}$
:
$\unicode[STIX]{x1D6EC}=\{\ast \}$
:
![]() $r=2$
,
$r=2$
,
![]() $\mathfrak{X}=((X,\emptyset );n=1,\unicode[STIX]{x1D6FC}=(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)\in (\boldsymbol{X}_{2}^{\mathsf{rel}})_{1})$
,
$\mathfrak{X}=((X,\emptyset );n=1,\unicode[STIX]{x1D6FC}=(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)\in (\boldsymbol{X}_{2}^{\mathsf{rel}})_{1})$
,
![]() $\unicode[STIX]{x1D703}=\text{id}_{[1]}$
. In this case the cycle that is supposed to represent the
$\unicode[STIX]{x1D703}=\text{id}_{[1]}$
. In this case the cycle that is supposed to represent the
![]() $(\mathfrak{X},\unicode[STIX]{x1D703})$
-component of
$(\mathfrak{X},\unicode[STIX]{x1D703})$
-component of
![]() $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(2)\ast }$
always does not satisfy the face condition. This is why we need the following constructions.
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(2)\ast }$
always does not satisfy the face condition. This is why we need the following constructions.
2.1.2 The generic hyperplanes
Let
![]() $\{{x_{ab}\}}_{1\leqslant a,b\leqslant r}$
be the coordinates of
$\{{x_{ab}\}}_{1\leqslant a,b\leqslant r}$
be the coordinates of
![]() $\text{GL}_{r}$
, so that its function field is
$\text{GL}_{r}$
, so that its function field is
![]() $k(\text{GL}_{r})=k({\{x_{ab}\}}_{a,b})$
. For each
$k(\text{GL}_{r})=k({\{x_{ab}\}}_{a,b})$
. For each
![]() $a\in \{1,\ldots ,r\}$
, let us consider the “generic translation” of the coordinates:
$a\in \{1,\ldots ,r\}$
, let us consider the “generic translation” of the coordinates:
![]() $T_{a}^{\circ }:=\sum _{b=1}^{r}T_{b}x_{ba}\in \unicode[STIX]{x1D6E4}(\mathbb{P}_{k(\text{GL}_{r})}^{r-1},{\mathcal{O}}(1))$
. As in Section 1.3, we are using the superscript
$T_{a}^{\circ }:=\sum _{b=1}^{r}T_{b}x_{ba}\in \unicode[STIX]{x1D6E4}(\mathbb{P}_{k(\text{GL}_{r})}^{r-1},{\mathcal{O}}(1))$
. As in Section 1.3, we are using the superscript
![]() $(-)^{\circ }$
to indicate the involvement of moving procedure. Applying the construction in Section 1.2 and Definition 1.14 on
$(-)^{\circ }$
to indicate the involvement of moving procedure. Applying the construction in Section 1.2 and Definition 1.14 on
![]() $T_{a}^{\circ }$
, we define cycles:
$T_{a}^{\circ }$
, we define cycles:
These objects are different from those denoted by similar symbols in Definition 1.14, but since the older ones are not going to be used again in this section, there is no risk of confusion.
2.1.3 Homotopy of the hyperplanes
The homotopy in equation (1) gives us cycles
and by pull-back as in Definition 1.14, we define
Definition 2.2. For a field extension
![]() $L/k$
, denote by
$L/k$
, denote by
![]() $p_{\ast }z_{L}^{i}$
(the nonmodulus cycle complex with scalar extension) the association of complexes
$p_{\ast }z_{L}^{i}$
(the nonmodulus cycle complex with scalar extension) the association of complexes
![]() $\mathfrak{X}\mapsto p_{\ast }z(\mathfrak{X}\otimes _{k}L)$
for objects of
$\mathfrak{X}\mapsto p_{\ast }z(\mathfrak{X}\otimes _{k}L)$
for objects of
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
. There is an obvious scalar extension map
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
. There is an obvious scalar extension map
![]() $p_{\ast }z^{i}\rightarrow p_{\ast }z_{L}^{i}$
.
$p_{\ast }z^{i}\rightarrow p_{\ast }z_{L}^{i}$
.
As in Remark 1.8, this is not a presheaf on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
unless one restricts to some nice subcategory. The set of cycles
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
unless one restricts to some nice subcategory. The set of cycles
![]() $\{\unicode[STIX]{x1D6E4}\text{}_{m,k(\text{GL}_{r})}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})\}_{m,\mathfrak{X},\unicode[STIX]{x1D703}}$
determines a map of complexes
$\{\unicode[STIX]{x1D6E4}\text{}_{m,k(\text{GL}_{r})}^{(a)\circ }(\mathfrak{X},\unicode[STIX]{x1D703})\}_{m,\mathfrak{X},\unicode[STIX]{x1D703}}$
determines a map of complexes
2.2 The open covering and the complex
 ${\mathcal{Z}}$
${\mathcal{Z}}$
Definition 2.3. Let
![]() $S\subset [n]$
be a subset consisting of
$S\subset [n]$
be a subset consisting of
![]() $m+1$
elements. We denote the unique injection
$m+1$
elements. We denote the unique injection
![]() $[m]{\hookrightarrow}[n]$
into
$[m]{\hookrightarrow}[n]$
into
![]() $S$
also by the same letter. Let us denote by
$S$
also by the same letter. Let us denote by
![]() $\unicode[STIX]{x1D6E4}\text{}^{(a)\ast }(S)$
the pull-back of
$\unicode[STIX]{x1D6E4}\text{}^{(a)\ast }(S)$
the pull-back of
![]() $\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\ast }$
by the map
$\unicode[STIX]{x1D6E4}\text{}_{m}^{(a)\ast }$
by the map
Of course, it is the divisor of the function
![]() $F\text{}^{(a)\ast }(S)$
similarly defined.
$F\text{}^{(a)\ast }(S)$
similarly defined.
Definition 2.4. Let
![]() $B_{n}\text{GL}_{r}^{\ast }$
be the following open subset of
$B_{n}\text{GL}_{r}^{\ast }$
be the following open subset of
![]() $B_{n}\text{GL}_{r}$
:
$B_{n}\text{GL}_{r}$
:
where
![]() $p\,:\,\mathbb{P}(E_{n}\text{GL}_{r})=\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}\rightarrow B_{n}\text{GL}_{r}$
is the second projection.
$p\,:\,\mathbb{P}(E_{n}\text{GL}_{r})=\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}\rightarrow B_{n}\text{GL}_{r}$
is the second projection.
It follows that a point
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})\in B_{n}\text{GL}_{r}(k(\unicode[STIX]{x1D6FC}))$
is in
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})\in B_{n}\text{GL}_{r}(k(\unicode[STIX]{x1D6FC}))$
is in
![]() $B_{n}\text{GL}_{r}^{\ast }$
if and only if for every choice of
$B_{n}\text{GL}_{r}^{\ast }$
if and only if for every choice of
![]() $0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
, the intersection in
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
, the intersection in
![]() $\mathbb{P}_{k(\unicode[STIX]{x1D6FC})}^{r-1}$
$\mathbb{P}_{k(\unicode[STIX]{x1D6FC})}^{r-1}$
is empty. Note that whenever
![]() $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are all upper triangular, the sequence
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are all upper triangular, the sequence
![]() $(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
belongs to
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
belongs to
![]() $B_{n}\text{GL}_{r}^{\ast }$
. The simplicial structure of
$B_{n}\text{GL}_{r}^{\ast }$
. The simplicial structure of
![]() $B\text{GL}_{r}$
restricts to the schemes
$B\text{GL}_{r}$
restricts to the schemes
![]() ${\{B_{n}\text{GL}_{r}^{\ast }\}}_{n}$
.
${\{B_{n}\text{GL}_{r}^{\ast }\}}_{n}$
.
Definition 2.5. For a datum
![]() $(\mathfrak{X},\unicode[STIX]{x1D703})$
of an object
$(\mathfrak{X},\unicode[STIX]{x1D703})$
of an object
![]() $\mathfrak{X}\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
and a map
$\mathfrak{X}\in \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
and a map
![]() $\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
, define an open subset
$\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
, define an open subset
![]() $X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
of
$X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
of
![]() $X$
by
$X$
by
![]() $X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }:=(B\text{GL}_{r}(\unicode[STIX]{x1D703})\circ \unicode[STIX]{x1D6FC})^{-1}(B_{n}\text{GL}_{r}^{\ast }).$
$X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }:=(B\text{GL}_{r}(\unicode[STIX]{x1D703})\circ \unicode[STIX]{x1D6FC})^{-1}(B_{n}\text{GL}_{r}^{\ast }).$
Definition 2.6. Define the simplicial subpresheaves
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
and
$\unicode[STIX]{x1D6E5}^{\ast }$
and
![]() $\unicode[STIX]{x1D6E5}^{\circ }$
of
$\unicode[STIX]{x1D6E5}^{\circ }$
of
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
by (where
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
by (where
![]() $\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
):
$\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})$
):
Also, set
![]() $\unicode[STIX]{x1D6E5}\text{}^{\circ \ast }:=\unicode[STIX]{x1D6E5}^{\circ }\cap \unicode[STIX]{x1D6E5}^{\ast }$
.
$\unicode[STIX]{x1D6E5}\text{}^{\circ \ast }:=\unicode[STIX]{x1D6E5}^{\circ }\cap \unicode[STIX]{x1D6E5}^{\ast }$
.
Let us say that a morphism of the form
![]() $(f,\text{id},\text{id})\,:\,\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$
in
$(f,\text{id},\text{id})\,:\,\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$
in
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
is an open immersion if the underlying morphism
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
is an open immersion if the underlying morphism
![]() $f\,:\,X^{\prime }\rightarrow X$
is an open immersion and if
$f\,:\,X^{\prime }\rightarrow X$
is an open immersion and if
![]() $D^{\prime }=X^{\prime }\times _{X}D$
. Then
$D^{\prime }=X^{\prime }\times _{X}D$
. Then
![]() $\unicode[STIX]{x1D6E5}^{\circ }$
and
$\unicode[STIX]{x1D6E5}^{\circ }$
and
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
are open subpresheaves of
$\unicode[STIX]{x1D6E5}^{\ast }$
are open subpresheaves of
![]() $\unicode[STIX]{x1D6E5}$
. The map
$\unicode[STIX]{x1D6E5}$
. The map
![]() $\unicode[STIX]{x1D6E5}^{\circ }\sqcup \unicode[STIX]{x1D6E5}^{\ast }\rightarrow \unicode[STIX]{x1D6E5}$
is not a surjection of Zariski sheaves, but becomes so on the smaller category
$\unicode[STIX]{x1D6E5}^{\circ }\sqcup \unicode[STIX]{x1D6E5}^{\ast }\rightarrow \unicode[STIX]{x1D6E5}$
is not a surjection of Zariski sheaves, but becomes so on the smaller category
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
introduced in Section 2.3. Consequently, the complex
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
introduced in Section 2.3. Consequently, the complex
![]() ${\mathcal{Z}}$
below becomes quasi-isomorphic to
${\mathcal{Z}}$
below becomes quasi-isomorphic to
![]() $\mathbb{Z}$
on that category.
$\mathbb{Z}$
on that category.
Definition 2.7. Define the complex
![]() ${\mathcal{Z}}$
on
${\mathcal{Z}}$
on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
by:
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
by:
The maps
![]() $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm},k(\text{GL}_{r})}^{(a)\circ }$
on
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm},k(\text{GL}_{r})}^{(a)\circ }$
on
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\circ }$
,
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\circ }$
,
![]() $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(a)\ast }$
on
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(a)\ast }$
on
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\ast }$
and the homotopy
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\ast }$
and the homotopy
![]() $\{\unicode[STIX]{x1D6E4}\text{}_{m,k(\text{GL}_{r})}^{(a)\circ \ast }\}_{m}$
on
$\{\unicode[STIX]{x1D6E4}\text{}_{m,k(\text{GL}_{r})}^{(a)\circ \ast }\}_{m}$
on
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\text{}^{\circ \ast }$
determine a map of complexes
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\text{}^{\circ \ast }$
determine a map of complexes
The next lemma follows from the definition of
![]() $B\text{GL}_{r}^{\ast }$
and the algebraic independence of
$B\text{GL}_{r}^{\ast }$
and the algebraic independence of
![]() ${\{x_{ab}\}}_{a,b}$
.
${\{x_{ab}\}}_{a,b}$
.
Lemma 2.8.
(i) The intersection of
 $\bigcap _{a=1}^{r}\unicode[STIX]{x1D6E4}\text{}_{0,k(\text{GL}_{r})}^{(a)\circ }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})$
and
$\bigcap _{a=1}^{r}\unicode[STIX]{x1D6E4}\text{}_{0,k(\text{GL}_{r})}^{(a)\circ }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})$
and
 $(\mathbb{P}^{r-1}\times X^{\circ })_{k(\text{GL}_{r})}$
is empty for every choice of
$(\mathbb{P}^{r-1}\times X^{\circ })_{k(\text{GL}_{r})}$
is empty for every choice of
 $0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
.
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
.(ii) The intersection of
 $\bigcap _{a=1}^{r}\unicode[STIX]{x1D6E4}\text{}_{0}^{(a)\ast }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})$
and
$\bigcap _{a=1}^{r}\unicode[STIX]{x1D6E4}\text{}_{0}^{(a)\ast }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})$
and
 $\mathbb{P}^{r-1}\times X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
is empty for every choice of
$\mathbb{P}^{r-1}\times X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
is empty for every choice of
 $0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
.
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
.(iii) The intersection of
 $(\mathbb{P}^{r-1}\times X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\circ \ast })_{k(\text{GL}_{r})}$
and: is empty for every choice of
$(\mathbb{P}^{r-1}\times X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\circ \ast })_{k(\text{GL}_{r})}$
and: is empty for every choice of $$\begin{eqnarray}\biggl(\mathop{\bigcap }_{a=1}^{b}\unicode[STIX]{x1D6E4}\text{}_{0,k(\text{GL}_{r})}^{(a)\circ }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})\biggr)\cap \biggl(\mathop{\bigcap }_{a=b+1}^{r}\unicode[STIX]{x1D6E4}\text{}_{0}^{(a)\ast }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})_{k(\text{GL}_{r})}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\mathop{\bigcap }_{a=1}^{b}\unicode[STIX]{x1D6E4}\text{}_{0,k(\text{GL}_{r})}^{(a)\circ }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})\biggr)\cap \biggl(\mathop{\bigcap }_{a=b+1}^{r}\unicode[STIX]{x1D6E4}\text{}_{0}^{(a)\ast }(\mathfrak{X},v_{\unicode[STIX]{x1D703}(k_{a})}^{[n]})_{k(\text{GL}_{r})}\biggr)\end{eqnarray}$$
 $0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
and
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{r}\leqslant n$
and
 $0\leqslant b\leqslant r$
.
$0\leqslant b\leqslant r$
.
By Lemma 2.8, we can apply Lemmas 1.10 and B.4 to conclude that the cup product
is well defined. We now introduce a modulus version
![]() $p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{i}\subset p_{\ast }z_{k(\text{GL}_{r})}^{i}$
of the target. We shall show that the map (5) factors through it when restricted to the category
$p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{i}\subset p_{\ast }z_{k(\text{GL}_{r})}^{i}$
of the target. We shall show that the map (5) factors through it when restricted to the category
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
introduced in Section 2.3.
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
introduced in Section 2.3.
Definition 2.9. For a field extension
![]() $L/k$
, define the presheaf of complexes
$L/k$
, define the presheaf of complexes
![]() $p_{\ast }z_{\mathsf{rel},L}^{i}$
(cycle complex with modulus with scalar extension) on
$p_{\ast }z_{\mathsf{rel},L}^{i}$
(cycle complex with modulus with scalar extension) on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
by the rule
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
by the rule
with the same presheaf structure as
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
. There is a scalar extension map
$p_{\ast }z_{\mathsf{rel}}^{i}$
. There is a scalar extension map
![]() $p_{\ast }z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }z_{\mathsf{rel},L}^{i}$
.
$p_{\ast }z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }z_{\mathsf{rel},L}^{i}$
.
This definition may appear strange at first glance. It is motivated by the fact that Bloch’s specialization map (Section 2.4) is available (and necessary) only when
![]() $D=\emptyset$
.
$D=\emptyset$
.
2.3 The relative Volodin space
Now we introduce the relative Volodin space presheaf. Its significance lies in its relation to the relative
![]() $K$
-theory; see Theorem 2.24.
$K$
-theory; see Theorem 2.24.
Definition 2.10. Let
![]() $(X,D)\in \mathsf{MSm}$
. Denote by
$(X,D)\in \mathsf{MSm}$
. Denote by
![]() $I=I_{D}\subset {\mathcal{O}}_{X}$
the ideal sheaf defining
$I=I_{D}\subset {\mathcal{O}}_{X}$
the ideal sheaf defining
![]() $D$
. Let
$D$
. Let
![]() $r\geqslant 0$
be a non-negative integer and
$r\geqslant 0$
be a non-negative integer and
![]() $\unicode[STIX]{x1D70E}$
a partial order on the set
$\unicode[STIX]{x1D70E}$
a partial order on the set
![]() $\{1,\ldots ,r\}$
. Then the subgroup
$\{1,\ldots ,r\}$
. Then the subgroup
![]() $T^{\unicode[STIX]{x1D70E}}(X,D)\subset \text{GL}_{r}(X)$
is defined to be the set of matrices
$T^{\unicode[STIX]{x1D70E}}(X,D)\subset \text{GL}_{r}(X)$
is defined to be the set of matrices
![]() $(x_{ab})_{1\leqslant a,b\leqslant r}$
such that
$(x_{ab})_{1\leqslant a,b\leqslant r}$
such that
![]() $x_{ab}\equiv \unicode[STIX]{x1D6FF}_{ab}\hspace{0.6em}{\rm mod}\hspace{0.2em}I_{D}$
(Kronecker’s
$x_{ab}\equiv \unicode[STIX]{x1D6FF}_{ab}\hspace{0.6em}{\rm mod}\hspace{0.2em}I_{D}$
(Kronecker’s
![]() $\unicode[STIX]{x1D6FF}$
) unless
$\unicode[STIX]{x1D6FF}$
) unless
![]() $a\overset{\unicode[STIX]{x1D70E}}{{<}}b$
. For example, if
$a\overset{\unicode[STIX]{x1D70E}}{{<}}b$
. For example, if
![]() $\unicode[STIX]{x1D70E}$
is the usual total order on
$\unicode[STIX]{x1D70E}$
is the usual total order on
![]() $\{1,2,3\}$
, then elements of
$\{1,2,3\}$
, then elements of
![]() $T^{\unicode[STIX]{x1D70E}}(X,D)$
look like:
$T^{\unicode[STIX]{x1D70E}}(X,D)$
look like:
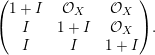 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1+I & {\mathcal{O}}_{X} & {\mathcal{O}}_{X}\\ I & 1+I & {\mathcal{O}}_{X}\\ I & I & 1+I\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1+I & {\mathcal{O}}_{X} & {\mathcal{O}}_{X}\\ I & 1+I & {\mathcal{O}}_{X}\\ I & I & 1+I\end{array}\right)\!.\end{eqnarray}$$
If another order
![]() $\unicode[STIX]{x1D70E}^{\prime }$
extends
$\unicode[STIX]{x1D70E}^{\prime }$
extends
![]() $\unicode[STIX]{x1D70E}$
(i.e., if
$\unicode[STIX]{x1D70E}$
(i.e., if
![]() $a\overset{\unicode[STIX]{x1D70E}}{{<}}b$
implies
$a\overset{\unicode[STIX]{x1D70E}}{{<}}b$
implies
![]() $a\overset{\unicode[STIX]{x1D70E}^{\prime }}{{<}}b$
), we have
$a\overset{\unicode[STIX]{x1D70E}^{\prime }}{{<}}b$
), we have
![]() $T^{\unicode[STIX]{x1D70E}}(X,D)\subset T^{\unicode[STIX]{x1D70E}^{\prime }}(X,D)$
. The Volodin space
$T^{\unicode[STIX]{x1D70E}}(X,D)\subset T^{\unicode[STIX]{x1D70E}^{\prime }}(X,D)$
. The Volodin space
![]() $\boldsymbol{X}_{r}(X,D)$
is the simplicial subset of
$\boldsymbol{X}_{r}(X,D)$
is the simplicial subset of
![]() $B\text{GL}_{r}(X)$
defined by
$B\text{GL}_{r}(X)$
defined by
We set
![]() $\boldsymbol{X}(X,D)=\mathop{\varinjlim }\nolimits_{r}\boldsymbol{X}_{r}(X,D)\subset B\text{GL}(X)$
. Define a Nisnevich sheaf
$\boldsymbol{X}(X,D)=\mathop{\varinjlim }\nolimits_{r}\boldsymbol{X}_{r}(X,D)\subset B\text{GL}(X)$
. Define a Nisnevich sheaf
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}$
on
$\boldsymbol{X}_{r}^{\mathsf{rel}}$
on
![]() $\mathsf{MSm}$
by
$\mathsf{MSm}$
by
![]() $(X,D)\mapsto \boldsymbol{X}_{r}(X,D)$
.
$(X,D)\mapsto \boldsymbol{X}_{r}(X,D)$
.
We also denote by
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}$
the presheaf induced by the forgetful functor
$\boldsymbol{X}_{r}^{\mathsf{rel}}$
the presheaf induced by the forgetful functor
![]() $\mathsf{MSm}^{\ast }\rightarrow \mathsf{MSm}$
. In particular, we have the site
$\mathsf{MSm}^{\ast }\rightarrow \mathsf{MSm}$
. In particular, we have the site
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
fibered over it. The inclusion
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
fibered over it. The inclusion
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}{\hookrightarrow}B\text{GL}_{r}$
induces a functor
$\boldsymbol{X}_{r}^{\mathsf{rel}}{\hookrightarrow}B\text{GL}_{r}$
induces a functor
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\rightarrow \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
. Every presheaf and map of presheaves on the latter restrict to the former. It follows for example that the projective bundle formula in Section 1 holds on
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\rightarrow \mathsf{MSm}^{\ast }/B\text{GL}_{r}$
. Every presheaf and map of presheaves on the latter restrict to the former. It follows for example that the projective bundle formula in Section 1 holds on
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
in the same form.
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
in the same form.
Lemma 2.11. The map of simplicial presheaves
![]() $\unicode[STIX]{x1D6E5}^{\circ }\sqcup \unicode[STIX]{x1D6E5}^{\ast }\rightarrow \unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}^{\circ }\sqcup \unicode[STIX]{x1D6E5}^{\ast }\rightarrow \unicode[STIX]{x1D6E5}$
on
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
is surjective in the Zariski topology.
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
is surjective in the Zariski topology.
Proof. It suffices to prove the following: For each
![]() $(X,D)\in \mathsf{MSm}^{\ast }$
,
$(X,D)\in \mathsf{MSm}^{\ast }$
,
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})\in B_{n}\text{GL}_{r}(X)$
and
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})\in B_{n}\text{GL}_{r}(X)$
and
![]() $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
, we have
$\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
, we have
![]() $X=(X\setminus D)\cup X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
.
$X=(X\setminus D)\cup X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
.
Let
![]() $\unicode[STIX]{x1D70E}$
be a (total) order on
$\unicode[STIX]{x1D70E}$
be a (total) order on
![]() $\{1,\ldots ,r\}$
such that
$\{1,\ldots ,r\}$
such that
![]() $\unicode[STIX]{x1D6FC}\in BT^{\unicode[STIX]{x1D70E}}(X,D)$
. The matrices
$\unicode[STIX]{x1D6FC}\in BT^{\unicode[STIX]{x1D70E}}(X,D)$
. The matrices
![]() $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are all upper triangular modulo
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are all upper triangular modulo
![]() $I_{D}$
up to permutation by
$I_{D}$
up to permutation by
![]() $\unicode[STIX]{x1D70E}$
. It follows from the remark subsequent to Definition 2.4 that every
$\unicode[STIX]{x1D70E}$
. It follows from the remark subsequent to Definition 2.4 that every
![]() $x\in D$
belongs to
$x\in D$
belongs to
![]() $X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
. This proves the lemma.
$X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }$
. This proves the lemma.
By Lemma 2.11, the complex
![]() ${\mathcal{Z}}$
is Zariski locally quasi-isomorphic to
${\mathcal{Z}}$
is Zariski locally quasi-isomorphic to
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\simeq \mathbb{Z}$
by the map
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\simeq \mathbb{Z}$
by the map
![]() $(\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\circ })\oplus (\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\ast })$
$(\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\circ })\oplus (\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\ast })$
![]() $\xrightarrow[{\text{incl.}\sqcup (-\text{incl.})}]{}$
$\xrightarrow[{\text{incl.}\sqcup (-\text{incl.})}]{}$
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}$
when restricted to
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}$
when restricted to
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
.
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
.
The rest of this subsection is devoted to the proof of the following:
Theorem 2.12. The map (5) restricted to
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
factors through the subcomplex
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
factors through the subcomplex
![]() $p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{r}$
.
$p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{r}$
.
Note that the assertion only concerns the part
![]() $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(r)\ast }\,:\,\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\ast }\rightarrow p_{\ast }z^{r}$
. The following criterion for the modulus condition will be useful.
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(r)\ast }\,:\,\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}^{\ast }\rightarrow p_{\ast }z^{r}$
. The following criterion for the modulus condition will be useful.
Definition 2.13. [Reference Binda and SaitoBS17, Section 4]
Let
![]() $A$
be a commutative ring with unit and
$A$
be a commutative ring with unit and
![]() $I$
be an ideal. A polynomial
$I$
be an ideal. A polynomial
is said to be admissible if
![]() $a_{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}}\in I^{\max _{i}\{\unicode[STIX]{x1D706}_{i}\}}$
and if
$a_{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}}\in I^{\max _{i}\{\unicode[STIX]{x1D706}_{i}\}}$
and if
![]() $a_{0,\ldots ,0}$
maps into
$a_{0,\ldots ,0}$
maps into
![]() $(A/I)^{\ast }$
.
$(A/I)^{\ast }$
.
Lemma 2.14. [Reference Binda and SaitoBS17, Lemma 4.3]
Let
![]() $X$
be an affine scheme equipped with an effective Cartier divisor
$X$
be an affine scheme equipped with an effective Cartier divisor
![]() $D$
. Let
$D$
. Let
![]() $V$
be an integral closed subscheme of
$V$
be an integral closed subscheme of
![]() $X\times \Box ^{n}$
. If the defining ideal for
$X\times \Box ^{n}$
. If the defining ideal for
![]() $V$
contains an admissible polynomial with respect to the defining ideal of
$V$
contains an admissible polynomial with respect to the defining ideal of
![]() $D$
, then
$D$
, then
![]() $V$
satisfies the modulus condition.
$V$
satisfies the modulus condition.
When
![]() $X$
is a
$X$
is a
![]() $k$
-scheme of finite type equipped with an ideal sheaf
$k$
-scheme of finite type equipped with an ideal sheaf
![]() $I$
, let us say that an ideal sheaf
$I$
, let us say that an ideal sheaf
![]() $J$
on
$J$
on
![]() $X\times \Box ^{n}$
is admissible if there exists an affine open covering
$X\times \Box ^{n}$
is admissible if there exists an affine open covering
![]() ${\{U_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}}$
of
${\{U_{\unicode[STIX]{x1D6FC}}\}}_{\unicode[STIX]{x1D6FC}}$
of
![]() $X$
such that
$X$
such that
![]() $J$
restricted to each
$J$
restricted to each
![]() $U_{\unicode[STIX]{x1D6FC}}\times \Box ^{n}$
contains an admissible polynomial with respect to
$U_{\unicode[STIX]{x1D6FC}}\times \Box ^{n}$
contains an admissible polynomial with respect to
![]() $I(U_{\unicode[STIX]{x1D6FC}})$
. Note that if
$I(U_{\unicode[STIX]{x1D6FC}})$
. Note that if
![]() $J$
is admissible and
$J$
is admissible and
![]() $f\,:\,X^{\prime }\rightarrow X$
is a morphism from another scheme, the ideal sheaf
$f\,:\,X^{\prime }\rightarrow X$
is a morphism from another scheme, the ideal sheaf
![]() $(f\times \text{id}_{\Box ^{n}})^{\ast }J$
on
$(f\times \text{id}_{\Box ^{n}})^{\ast }J$
on
![]() $X^{\prime }\times \Box ^{n}$
is admissible with respect to
$X^{\prime }\times \Box ^{n}$
is admissible with respect to
![]() $f^{\ast }I$
, because elements in a power
$f^{\ast }I$
, because elements in a power
![]() $I^{\unicode[STIX]{x1D706}}$
pull back into the power
$I^{\unicode[STIX]{x1D706}}$
pull back into the power
![]() $(f^{\ast }I)^{\unicode[STIX]{x1D706}}$
.
$(f^{\ast }I)^{\unicode[STIX]{x1D706}}$
.
Notation 2.15. Let
![]() $\{x_{bc}^{i_{}^{}\}}$
be the coordinates for
$\{x_{bc}^{i_{}^{}\}}$
be the coordinates for
![]() $B_{n}\text{GL}_{r}=(\text{GL}_{r})^{n}$
. For an ordering
$B_{n}\text{GL}_{r}=(\text{GL}_{r})^{n}$
. For an ordering
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $\{1,\ldots ,r\}$
, let
$\{1,\ldots ,r\}$
, let
![]() $I^{\unicode[STIX]{x1D70E}}$
be the ideal of
$I^{\unicode[STIX]{x1D70E}}$
be the ideal of
![]() ${\mathcal{O}}_{B_{n}\text{GL}_{r}}$
generated by
${\mathcal{O}}_{B_{n}\text{GL}_{r}}$
generated by
![]() $x_{bc}^{i}-\unicode[STIX]{x1D6FF}_{bc}$
with
$x_{bc}^{i}-\unicode[STIX]{x1D6FF}_{bc}$
with
![]() $i\in \{1,\ldots ,n\}$
and
$i\in \{1,\ldots ,n\}$
and
![]() $b,c\in \{1,\ldots ,r\}$
such that
$b,c\in \{1,\ldots ,r\}$
such that
![]() $b\overset{\unicode[STIX]{x1D70E}}{\not <}c$
, where
$b\overset{\unicode[STIX]{x1D70E}}{\not <}c$
, where
![]() $\unicode[STIX]{x1D6FF}_{bc}$
is Kronecker’s delta.
$\unicode[STIX]{x1D6FF}_{bc}$
is Kronecker’s delta.
Under this notation, a section
![]() $\unicode[STIX]{x1D6FC}\in (\boldsymbol{X}_{r}^{\mathsf{rel}})_{n}(X,D)$
is the same as a morphism of schemes
$\unicode[STIX]{x1D6FC}\in (\boldsymbol{X}_{r}^{\mathsf{rel}})_{n}(X,D)$
is the same as a morphism of schemes
![]() $X\rightarrow B_{n}\text{GL}_{r}$
which maps the subscheme
$X\rightarrow B_{n}\text{GL}_{r}$
which maps the subscheme
![]() $D$
into the closed subscheme
$D$
into the closed subscheme
![]() $V(I^{\unicode[STIX]{x1D70E}})$
for some
$V(I^{\unicode[STIX]{x1D70E}})$
for some
![]() $\unicode[STIX]{x1D70E}$
. For subsets
$\unicode[STIX]{x1D70E}$
. For subsets
![]() $S,T\subset [n]$
, let us write
$S,T\subset [n]$
, let us write
![]() $S\leqslant T$
to mean
$S\leqslant T$
to mean
![]() $s\leqslant t$
for all
$s\leqslant t$
for all
![]() $s\in S$
and
$s\in S$
and
![]() $t\in T$
. Also, recall the symbol
$t\in T$
. Also, recall the symbol
![]() $F\text{}^{(a)\ast }(S)$
from Definition 2.3.
$F\text{}^{(a)\ast }(S)$
from Definition 2.3.
Proof of Theorem 2.12.
The cycles defining the map
![]() $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(r)\ast }$
are pull-backs of the universal cycles on
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)\ast }\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(r)\ast }$
are pull-backs of the universal cycles on
![]() $\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}^{\ast }\times \Box ^{n}$
by individual maps
$\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}^{\ast }\times \Box ^{n}$
by individual maps
![]() $\mathbb{P}^{r-1}\times X\times \Box ^{n}\rightarrow \mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}^{\ast }\times \Box ^{n}$
. In view of Lemma 2.14 and this observation, Theorem 2.12 follows from the following lemma.
$\mathbb{P}^{r-1}\times X\times \Box ^{n}\rightarrow \mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}^{\ast }\times \Box ^{n}$
. In view of Lemma 2.14 and this observation, Theorem 2.12 follows from the following lemma.
Lemma 2.16. Let
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $r\geqslant 1$
be integers and
$r\geqslant 1$
be integers and
![]() $\unicode[STIX]{x1D70E}$
an order on
$\unicode[STIX]{x1D70E}$
an order on
![]() $\{1,\ldots ,r\}$
. Let
$\{1,\ldots ,r\}$
. Let
![]() $S_{1}\leqslant \ldots \leqslant S_{r}$
be nonempty subsets of
$S_{1}\leqslant \ldots \leqslant S_{r}$
be nonempty subsets of
![]() $[n]$
. Then the ideal sheaf on
$[n]$
. Then the ideal sheaf on
![]() $\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}\times \Box ^{n}$
associated to the homogeneous ideal generated by:
$\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}\times \Box ^{n}$
associated to the homogeneous ideal generated by:
is admissible with respect to the ideal sheaf
![]() ${\mathcal{O}}_{\mathbb{P}^{r-1}}\otimes _{k}I^{\unicode[STIX]{x1D70E}}$
on
${\mathcal{O}}_{\mathbb{P}^{r-1}}\otimes _{k}I^{\unicode[STIX]{x1D70E}}$
on
![]() $\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}$
.
$\mathbb{P}^{r-1}\times B_{n}\text{GL}_{r}$
.
Lemma 2.16 follows from a more precise claim below. Note that we may obviously assume that
![]() $\unicode[STIX]{x1D70E}$
is a total order and, by symmetry, that
$\unicode[STIX]{x1D70E}$
is a total order and, by symmetry, that
![]() $\unicode[STIX]{x1D70E}$
is the usual order
$\unicode[STIX]{x1D70E}$
is the usual order
![]() $\unicode[STIX]{x1D70E}=\{1<\cdots <r\}$
. Let us write
$\unicode[STIX]{x1D70E}=\{1<\cdots <r\}$
. Let us write
![]() $I:=I^{\unicode[STIX]{x1D70E}}$
for this
$I:=I^{\unicode[STIX]{x1D70E}}$
for this
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
For
![]() $S\subset \{1,\ldots ,n\}$
, let us denote by
$S\subset \{1,\ldots ,n\}$
, let us denote by
![]() $[t_{i}\mid i\in S]\subset k[t_{1},\ldots ,t_{n}]$
the
$[t_{i}\mid i\in S]\subset k[t_{1},\ldots ,t_{n}]$
the
![]() $2^{|S|}$
-dimensional
$2^{|S|}$
-dimensional
![]() $k$
-vector space spanned by monomials
$k$
-vector space spanned by monomials
![]() $\prod _{i\in S}t_{i}^{\unicode[STIX]{x1D716}_{i}}$
where
$\prod _{i\in S}t_{i}^{\unicode[STIX]{x1D716}_{i}}$
where
![]() $\unicode[STIX]{x1D716}_{i}\in \{0,1\}$
. To ease the notation, we shall use the phrase:
$\unicode[STIX]{x1D716}_{i}\in \{0,1\}$
. To ease the notation, we shall use the phrase:
“a polynomial of the form
![]() $T_{c}\cdot I\cdot [t_{i}\mid i\in S]$
” (
$T_{c}\cdot I\cdot [t_{i}\mid i\in S]$
” (
![]() $c\in \{1,\ldots ,r\}$
)
$c\in \{1,\ldots ,r\}$
)
to mean a sum of polynomials of the form
![]() $T_{c}\cdot x\cdot f$
with
$T_{c}\cdot x\cdot f$
with
![]() $x\in I\subset k[x_{ab}^{i}]$
and
$x\in I\subset k[x_{ab}^{i}]$
and
![]() $f\in [t_{i}\mid i\in S]$
. For a nonempty subset
$f\in [t_{i}\mid i\in S]$
. For a nonempty subset
![]() $S$
of
$S$
of
![]() $[n]$
, we write
$[n]$
, we write
![]() $S^{\prime }$
for the set
$S^{\prime }$
for the set
![]() $S\setminus \{$
the minimum element of
$S\setminus \{$
the minimum element of
![]() $S\}$
.
$S\}$
.
Claim 2.17. For any
![]() $a\in \{1,\ldots ,r\}$
, the ideal of the polynomial ring
$a\in \{1,\ldots ,r\}$
, the ideal of the polynomial ring
generated by
![]() $\{F\text{}^{(b)\ast }(S_{b})\}_{a\leqslant b\leqslant r}$
contains a polynomial of the form
$\{F\text{}^{(b)\ast }(S_{b})\}_{a\leqslant b\leqslant r}$
contains a polynomial of the form
Claim 2.17 implies Lemma 2.16 because formula (6a
) divided by
![]() $T_{a}$
gives an admissible polynomial over the affine open set
$T_{a}$
gives an admissible polynomial over the affine open set
![]() $\{T_{a}\neq 0\}$
.
$\{T_{a}\neq 0\}$
.
Proof of Claim. We proceed by descending induction on the index
![]() $a$
starting with
$a$
starting with
![]() $a=r$
. Let us write down the definition of
$a=r$
. Let us write down the definition of
![]() $F\text{}^{(a)\ast }(S)$
, where
$F\text{}^{(a)\ast }(S)$
, where
![]() $a\in \{1,\ldots ,r\}$
and
$a\in \{1,\ldots ,r\}$
and
![]() $S\subset [n]$
is a nonempty subset with
$S\subset [n]$
is a nonempty subset with
![]() $s+1$
elements:
$s+1$
elements:
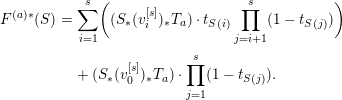 $$\begin{eqnarray}\displaystyle F\text{}^{(a)\ast }(S) & = & \displaystyle \mathop{\sum }_{i=1}^{s}\biggl((S_{\ast }(v_{i}^{[s]})_{\ast }T_{a})\cdot t_{S(i)}\mathop{\prod }_{j=i+1}^{s}(1-t_{S(j)})\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(S_{\ast }(v_{0}^{[s]})_{\ast }T_{a})\cdot \mathop{\prod }_{j=1}^{s}(1-t_{S(j)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F\text{}^{(a)\ast }(S) & = & \displaystyle \mathop{\sum }_{i=1}^{s}\biggl((S_{\ast }(v_{i}^{[s]})_{\ast }T_{a})\cdot t_{S(i)}\mathop{\prod }_{j=i+1}^{s}(1-t_{S(j)})\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,(S_{\ast }(v_{0}^{[s]})_{\ast }T_{a})\cdot \mathop{\prod }_{j=1}^{s}(1-t_{S(j)}).\nonumber\end{eqnarray}$$
Since we are in the group
![]() $T(X,D)$
of upper triangular matrices modulo
$T(X,D)$
of upper triangular matrices modulo
![]() $I$
, for any map
$I$
, for any map
![]() $v\,:\,[0]\rightarrow [n]$
(such as
$v\,:\,[0]\rightarrow [n]$
(such as
![]() $S\circ v_{i}^{[s]}$
) the function
$S\circ v_{i}^{[s]}$
) the function
![]() $v_{\ast }T_{a}$
has the form
$v_{\ast }T_{a}$
has the form
where
![]() ${\mathcal{O}}:={\mathcal{O}}_{B_{n}\text{GL}_{r}}$
. By these two formulas and the identity
${\mathcal{O}}:={\mathcal{O}}_{B_{n}\text{GL}_{r}}$
. By these two formulas and the identity
![]() $t_{S(s)}+t_{S(s-1)}(1-t_{S(s)})+\cdots +(1-t_{S(1)})\cdots (1-t_{S(s)})=1$
, we get:
$t_{S(s)}+t_{S(s-1)}(1-t_{S(s)})+\cdots +(1-t_{S(1)})\cdots (1-t_{S(s)})=1$
, we get:
This already proves the assertion for
![]() $a=r$
.
$a=r$
.
Now suppose
![]() $a<r$
. By descending induction, we know that the ideal in question contains polynomials of the form (
$a<r$
. By descending induction, we know that the ideal in question contains polynomials of the form (
![]() $6b$
) for
$6b$
) for
![]() $b=a+1,\ldots ,r$
. In particular, we get:
$b=a+1,\ldots ,r$
. In particular, we get:
modulo the ideal in question. Here we used the fact that the product of an element in
![]() $[t_{i}\mid i\in S]$
and one in
$[t_{i}\mid i\in S]$
and one in
![]() $[t_{i}\mid i\in T]$
with
$[t_{i}\mid i\in T]$
with
![]() $S\cap T=\emptyset$
belongs to
$S\cap T=\emptyset$
belongs to
![]() $[t_{i}\mid i\in S\cup T]$
. The last two formulas give a formula of the form (6a
). This completes the proof of Claim 2.17, hence also of Theorem 2.12.
$[t_{i}\mid i\in S\cup T]$
. The last two formulas give a formula of the form (6a
). This completes the proof of Claim 2.17, hence also of Theorem 2.12.
Hence we have obtained a map
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
.
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
.
2.4 Specialization map, and end of construction of
 $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
Bloch defined a specialization map
![]() $z^{i}(X_{L},\bullet )\rightarrow z^{i}(X,\bullet )$
in the derived category when
$z^{i}(X_{L},\bullet )\rightarrow z^{i}(X,\bullet )$
in the derived category when
![]() $L/k$
is a purely transcendental extension of finite degree equipped with a transcendence basis and
$L/k$
is a purely transcendental extension of finite degree equipped with a transcendence basis and
![]() $X$
is an equidimensional
$X$
is an equidimensional
![]() $k$
-scheme [Reference BlochBl86, pages 291, 292]. Likewise, we can define a specialization map
$k$
-scheme [Reference BlochBl86, pages 291, 292]. Likewise, we can define a specialization map
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
by using his map when
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
by using his map when
![]() $D=\emptyset$
and setting it to be the identity when
$D=\emptyset$
and setting it to be the identity when
![]() $D\neq \emptyset$
, roughly speaking. See Appendix B.4 for a careful definition.
$D\neq \emptyset$
, roughly speaking. See Appendix B.4 for a careful definition.
This applies in particular to the field
![]() $L=k(\text{GL}_{r})$
. Since the specialization map depends on the transcendental basis and the order thereof, we fix a total order on the set
$L=k(\text{GL}_{r})$
. Since the specialization map depends on the transcendental basis and the order thereof, we fix a total order on the set
![]() $\mathbb{N}\times \mathbb{N}$
once and for all, and use the induced order on the variables
$\mathbb{N}\times \mathbb{N}$
once and for all, and use the induced order on the variables
![]() $\{{x_{ab}\}}_{(a,b)\in \{1,\ldots ,r\}^{2}}$
.
$\{{x_{ab}\}}_{(a,b)\in \{1,\ldots ,r\}^{2}}$
.
Definition-Lemma 2.18. We define the map
![]() $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
in
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
by:
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
by:
It does not depend on the choice of the ordering.
Proof. Suppose that two consecutive variables in a given order are interchanged. Via the corresponding automorphism on
![]() $k(\text{GL}_{r})$
and hence on
$k(\text{GL}_{r})$
and hence on
![]() $p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{r}$
, the problem is equivalent to the situation where the specialization map stays the same but the map
$p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{r}$
, the problem is equivalent to the situation where the specialization map stays the same but the map
![]() ${\mathcal{Z}}\rightarrow p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{r}$
is constructed with the two variables interchanged. But this difference is within homotopy by the homotopy at the end of Section 1.2.
${\mathcal{Z}}\rightarrow p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r})}^{r}$
is constructed with the two variables interchanged. But this difference is within homotopy by the homotopy at the end of Section 1.2.
Remark 2.19. We will need to know that some cycles we have defined so far have certain alternative constructions when the base is restricted.
(i) After the restriction of the base
 $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}{\hookrightarrow}\boldsymbol{X}_{r+s}^{\,\mathsf{rel}}$
, the map
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}{\hookrightarrow}\boldsymbol{X}_{r+s}^{\,\mathsf{rel}}$
, the map
 $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r+s}$
(on the level of presheaf map
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r+s}$
(on the level of presheaf map
 ${\mathcal{Z}}\rightarrow p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r+s})}^{r+s}$
) can be defined using the alternative
${\mathcal{Z}}\rightarrow p_{\ast }z_{\mathsf{rel},k(\text{GL}_{r+s})}^{r+s}$
) can be defined using the alternative
 $T_{a}^{\circ }$
as follows:
$T_{a}^{\circ }$
as follows:
 $T_{a}^{\circ }:=\sum _{b=1}^{r}T_{b}x_{ba}$
if
$T_{a}^{\circ }:=\sum _{b=1}^{r}T_{b}x_{ba}$
if
 $1\leqslant a\leqslant r$
, and
$1\leqslant a\leqslant r$
, and
 $T_{a}^{\circ }:=\sum _{b=r}^{r+s}T_{b}x_{ba}$
if
$T_{a}^{\circ }:=\sum _{b=r}^{r+s}T_{b}x_{ba}$
if
 $r+1\leqslant a\leqslant r+s$
. This works because the proper intersection condition needed is now weaker (i.e., an analog of Lemma 2.8 is true with this
$r+1\leqslant a\leqslant r+s$
. This works because the proper intersection condition needed is now weaker (i.e., an analog of Lemma 2.8 is true with this
 $T_{a}^{\circ }$
on
$T_{a}^{\circ }$
on
 $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
). In this case, it is defined over the subfield
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
). In this case, it is defined over the subfield
 $k(\text{GL}_{r}\times \text{GL}_{s})$
of
$k(\text{GL}_{r}\times \text{GL}_{s})$
of
 $k(\text{GL}_{r+s})$
(the inclusion comes from the projection
$k(\text{GL}_{r+s})$
(the inclusion comes from the projection
 $M_{r+s}\rightarrow M_{r}\times M_{s}$
of the spaces of matrices).
$M_{r+s}\rightarrow M_{r}\times M_{s}$
of the spaces of matrices).(ii) In Section 1.11, we defined maps (for
 $j\leqslant r-1$
) using cycles given by the Friedlander–Lawson moving lemma. On the smaller category
$j\leqslant r-1$
) using cycles given by the Friedlander–Lawson moving lemma. On the smaller category $$\begin{eqnarray}p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}\,:\,\quad z_{\mathsf{rel}}^{i-j}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}\quad \text{ in }D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})\end{eqnarray}$$
$$\begin{eqnarray}p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}\,:\,\quad z_{\mathsf{rel}}^{i-j}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}\quad \text{ in }D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})\end{eqnarray}$$
 $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
, it can be constructed in the style of this Section 2. Namely we use the maps
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
, it can be constructed in the style of this Section 2. Namely we use the maps
 $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(a)}$
in formula (4) (actually, any choice of
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(a)}$
in formula (4) (actually, any choice of $$\begin{eqnarray}C_{\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}}^{j}:=\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(j)}\,:\,{\mathcal{Z}}\rightarrow p_{\ast }z_{k(\text{GL}_{r})}^{j}\end{eqnarray}$$
$$\begin{eqnarray}C_{\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}}^{j}:=\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(j)}\,:\,{\mathcal{Z}}\rightarrow p_{\ast }z_{k(\text{GL}_{r})}^{j}\end{eqnarray}$$
 $j$
members out of
$j$
members out of
 $\{1,\ldots ,r\}$
will do, in place of
$\{1,\ldots ,r\}$
will do, in place of
 $1,\ldots ,j$
), and use the specialization map. When
$1,\ldots ,j$
), and use the specialization map. When
 $j=r$
, this is the same as the construction of
$j=r$
, this is the same as the construction of
 $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
, so it is well defined also for
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
, so it is well defined also for
 $j=r$
. Again, when we restrict the base from
$j=r$
. Again, when we restrict the base from
 $\boldsymbol{X}_{r+s}^{\,\mathsf{rel}}$
to
$\boldsymbol{X}_{r+s}^{\,\mathsf{rel}}$
to
 $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
as in (i), we can use the simpler choice of
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
as in (i), we can use the simpler choice of
 $T_{a}^{\circ }$
(which are built in
$T_{a}^{\circ }$
(which are built in
 $\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(a)}$
).
$\unicode[STIX]{x1D6E4}\text{}_{\mathsf{MSm}}^{(a)}$
).
2.5 Chern classes on the relative Volodin space
Let
![]() $r>0$
. In Theorem 1.11, we have proved an isomorphism
$r>0$
. In Theorem 1.11, we have proved an isomorphism
in
![]() $D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
, and thus in
$D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
, and thus in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
. In Definition-Lemma 2.18, we have constructed a map
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
. In Definition-Lemma 2.18, we have constructed a map
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
. It follows that there are unique morphisms
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
. It follows that there are unique morphisms
![]() $c_{i}\,:\,\mathbb{Z}\rightarrow z_{\mathsf{rel}}^{i}$
in
$c_{i}\,:\,\mathbb{Z}\rightarrow z_{\mathsf{rel}}^{i}$
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
for
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}})$
for
![]() $1\leqslant i\leqslant r$
which satisfy the equality of maps
$1\leqslant i\leqslant r$
which satisfy the equality of maps
![]() $\mathbb{Z}\rightrightarrows p_{\ast }z_{\mathsf{rel}}^{r}$
:
$\mathbb{Z}\rightrightarrows p_{\ast }z_{\mathsf{rel}}^{r}$
:
It is convenient to define
![]() $c_{i}:=0$
for
$c_{i}:=0$
for
![]() $i>r$
. By Theorem A.5 applied to
$i>r$
. By Theorem A.5 applied to
![]() ${\mathcal{C}}=\mathsf{MSm}^{\ast }$
, we have an isomorphism
${\mathcal{C}}=\mathsf{MSm}^{\ast }$
, we have an isomorphism
Denote again by
![]() $c_{i}$
the corresponding map
$c_{i}$
the corresponding map
![]() $c_{i}\,:\,\boldsymbol{X}_{r}^{\mathsf{rel}}\rightarrow K(z_{\mathsf{rel}}^{i},0)$
in the Nisnevich-local homotopy category of simplicial presheaves
$c_{i}\,:\,\boldsymbol{X}_{r}^{\mathsf{rel}}\rightarrow K(z_{\mathsf{rel}}^{i},0)$
in the Nisnevich-local homotopy category of simplicial presheaves
![]() $\mathsf{Ho}(s\mathsf{PSh}(\mathsf{MSm}^{\ast }))$
.
$\mathsf{Ho}(s\mathsf{PSh}(\mathsf{MSm}^{\ast }))$
.
Definition 2.20. The above-defined maps:
are called the Chern classes (of rank
![]() $r$
).
$r$
).
Note that for every
![]() $r,i\geqslant 1$
the composite in
$r,i\geqslant 1$
the composite in
![]() $\mathsf{Ho}(s\mathsf{PSh}(\mathsf{MSm}^{\ast }))$
:
$\mathsf{Ho}(s\mathsf{PSh}(\mathsf{MSm}^{\ast }))$
:
equals the constant map to the base point because the map
![]() $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
is represented by the empty cycle when restricted to
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}$
is represented by the empty cycle when restricted to
![]() $\mathsf{MSm}^{\ast }/\{\text{id}\}$
. By this fact and a somewhat standard result below, it follows that
$\mathsf{MSm}^{\ast }/\{\text{id}\}$
. By this fact and a somewhat standard result below, it follows that
![]() $c_{i}$
come from unique maps
$c_{i}$
come from unique maps
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}\rightarrow K(z_{\mathsf{rel}}^{i},0)$
in
$\boldsymbol{X}_{r}^{\mathsf{rel}}\rightarrow K(z_{\mathsf{rel}}^{i},0)$
in
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
, the homotopy category of pointed simplicial presheaves.
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
, the homotopy category of pointed simplicial presheaves.
Lemma 2.21. cf. [Reference Asakura and SatoAS13, Proposition 5.2]
Let
![]() $(X,x)$
be a pointed object in
$(X,x)$
be a pointed object in
![]() $s\mathsf{PSh}(\mathsf{MSm}^{\ast })$
and
$s\mathsf{PSh}(\mathsf{MSm}^{\ast })$
and
![]() $(K,e_{K})$
be a group object in the same category. Then the square of sets below is cartesian:
$(K,e_{K})$
be a group object in the same category. Then the square of sets below is cartesian:

where the left vertical arrow is the “forget the base point” map and the right vertical arrow maps the point to the constant map at
![]() $e_{K}$
.
$e_{K}$
.
Next, associated with the embedding
![]() $\unicode[STIX]{x1D704}\,:\,\text{GL}_{r}{\hookrightarrow}\text{GL}_{r+1};~\unicode[STIX]{x1D6FC}\mapsto \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & 0\\ 0 & 1\end{array}\right)$
, we have embeddings
$\unicode[STIX]{x1D704}\,:\,\text{GL}_{r}{\hookrightarrow}\text{GL}_{r+1};~\unicode[STIX]{x1D6FC}\mapsto \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & 0\\ 0 & 1\end{array}\right)$
, we have embeddings
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}{\hookrightarrow}\boldsymbol{X}_{r+1}^{\mathsf{rel}}$
and
$\boldsymbol{X}_{r}^{\mathsf{rel}}{\hookrightarrow}\boldsymbol{X}_{r+1}^{\mathsf{rel}}$
and
![]() $\mathbb{P}^{r-1}{\hookrightarrow}\mathbb{P}^{r};(T_{1}:\ldots :T_{r})\mapsto (T_{1}:\ldots :T_{r}:0)$
. The following is a special case of Proposition 3.4.
$\mathbb{P}^{r-1}{\hookrightarrow}\mathbb{P}^{r};(T_{1}:\ldots :T_{r})\mapsto (T_{1}:\ldots :T_{r}:0)$
. The following is a special case of Proposition 3.4.
Lemma 2.22. The following diagram in
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
:
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
:

commutes for
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
2.6 Chern classes on the relative K-theory
We let
![]() $\text{K}$
be a functorial model of Thomason–Trobaugh’s
$\text{K}$
be a functorial model of Thomason–Trobaugh’s
![]() $K$
-theory [Reference Thomason and TrobaughTT90, 3.1], that is, it is a presheaf of spectra
$K$
-theory [Reference Thomason and TrobaughTT90, 3.1], that is, it is a presheaf of spectra
![]() $\text{K}$
such that for every quasicompact quasiseparated scheme
$\text{K}$
such that for every quasicompact quasiseparated scheme
![]() $X$
,
$X$
,
![]() $\text{K}(X)$
is the
$\text{K}(X)$
is the
![]() $K$
-theory spectrum of the Waldhausen category of perfect complexes on
$K$
-theory spectrum of the Waldhausen category of perfect complexes on
![]() $X$
.
$X$
.
Definition 2.23.
(i) We define a presheaf
 $\text{K}^{\mathsf{rel}}$
of spectra on
$\text{K}^{\mathsf{rel}}$
of spectra on
 $\mathsf{MSm}$
by
$\mathsf{MSm}$
by  $$\begin{eqnarray}\text{K}^{\mathsf{rel}}((X,D))=\text{K}(X,D)=\operatorname{hofib}(\text{K}(X)\rightarrow \text{K}(D)).\end{eqnarray}$$
$$\begin{eqnarray}\text{K}^{\mathsf{rel}}((X,D))=\text{K}(X,D)=\operatorname{hofib}(\text{K}(X)\rightarrow \text{K}(D)).\end{eqnarray}$$
(ii) We define a presheaf
 $\mathbb{Z}^{\mathsf{rel}}$
on
$\mathbb{Z}^{\mathsf{rel}}$
on
 $\mathsf{MSm}$
by
$\mathsf{MSm}$
by  $$\begin{eqnarray}\mathbb{Z}^{\mathsf{rel}}((X,D))=\left\{\begin{array}{@{}ll@{}}\mathbb{Z}\quad & \text{if }D=\emptyset ,\\ 0\quad & \text{if }D\neq \emptyset .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}^{\mathsf{rel}}((X,D))=\left\{\begin{array}{@{}ll@{}}\mathbb{Z}\quad & \text{if }D=\emptyset ,\\ 0\quad & \text{if }D\neq \emptyset .\end{array}\right.\end{eqnarray}$$
We use Bousfield–Kan’s
![]() $\mathbb{Z}$
-completion in [Reference Bousfield and KanBK72] as a functorial model of Quillen’s plus construction. The
$\mathbb{Z}$
-completion in [Reference Bousfield and KanBK72] as a functorial model of Quillen’s plus construction. The
![]() $\mathbb{Z}$
-completion is an endofunctor
$\mathbb{Z}$
-completion is an endofunctor
![]() $\mathbb{Z}_{\infty }\,:\,{\mathcal{S}}\rightarrow {\mathcal{S}}$
of the category of spaces (= simplicial sets) with a natural transformation
$\mathbb{Z}_{\infty }\,:\,{\mathcal{S}}\rightarrow {\mathcal{S}}$
of the category of spaces (= simplicial sets) with a natural transformation
![]() $\text{Id}_{{\mathcal{S}}}\rightarrow \mathbb{Z}_{\infty }$
. We will apply
$\text{Id}_{{\mathcal{S}}}\rightarrow \mathbb{Z}_{\infty }$
. We will apply
![]() $\mathbb{Z}_{\infty }$
sectionwise to simplicial presheaves.
$\mathbb{Z}_{\infty }$
sectionwise to simplicial presheaves.
The following is a relative and functorial version of Quillen’s “
![]() $+=Q$
” theorem.
$+=Q$
” theorem.
Theorem 2.24. There exists an isomorphism
in
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}))$
.Footnote
2
Under this isomorphism, the multiplication of
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}))$
.Footnote
2
Under this isomorphism, the multiplication of
![]() $\unicode[STIX]{x1D6FA}^{\infty }\text{K}^{\mathsf{rel}}$
coming from loop composition is compatible with the one of
$\unicode[STIX]{x1D6FA}^{\infty }\text{K}^{\mathsf{rel}}$
coming from loop composition is compatible with the one of
![]() $\mathbb{Z}^{\mathsf{rel}}\times \mathbb{Z}_{\infty }\boldsymbol{X}^{\mathsf{rel}}$
coming from the group law of
$\mathbb{Z}^{\mathsf{rel}}\times \mathbb{Z}_{\infty }\boldsymbol{X}^{\mathsf{rel}}$
coming from the group law of
![]() $\mathbb{Z}$
and the diagonal sum of matrices.
$\mathbb{Z}$
and the diagonal sum of matrices.
Proof. As in [Reference LodayLo98, 11.3.6], for any ring
![]() $A$
with an ideal
$A$
with an ideal
![]() $I$
, there exists an isomorphism
$I$
, there exists an isomorphism
The construction of the isomorphism can be functorial for the connected components (cf. [Reference GilletGi81, Proposition 2.15] for the case
![]() $I=0$
), and thus the desired isomorphism follows. We can verify easily that each step of the construction of the isomorphism is compatible with the multiplications.
$I=0$
), and thus the desired isomorphism follows. We can verify easily that each step of the construction of the isomorphism is compatible with the multiplications.
Theorem 2.25. For
![]() $r\geqslant 2l+2$
, the canonical map
$r\geqslant 2l+2$
, the canonical map
is a Zariski-local
![]() $l$
-equivalence of simplicial presheaves on
$l$
-equivalence of simplicial presheaves on
![]() $\mathsf{MSm}$
, that is, a Zariski-local weak equivalence after taking the
$\mathsf{MSm}$
, that is, a Zariski-local weak equivalence after taking the
![]() $l$
th Postnikov filtration.
$l$
th Postnikov filtration.
Proof. By Suslin’s stability as formulated in [Reference BeilinsonBe14, Section 5], for any local ring
![]() $A$
with an ideal
$A$
with an ideal
![]() $I$
, the canonical map
$I$
, the canonical map
![]() $\boldsymbol{X}_{r}(A,I)\rightarrow \boldsymbol{X}(A,I)$
induces homology isomorphisms in degree less or equal to
$\boldsymbol{X}_{r}(A,I)\rightarrow \boldsymbol{X}(A,I)$
induces homology isomorphisms in degree less or equal to
![]() $(r-1)/2$
. Then it follows from [Reference Bousfield and KanBK72, Chapter I 6.2] that the morphism
$(r-1)/2$
. Then it follows from [Reference Bousfield and KanBK72, Chapter I 6.2] that the morphism
is an isomorphism for
![]() $l\leqslant (r-2)/2$
. This proves the theorem.
$l\leqslant (r-2)/2$
. This proves the theorem.
In Definition 2.20, we have constructed maps
for
![]() $1\leqslant i\leqslant r$
in
$1\leqslant i\leqslant r$
in
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. Let
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. Let
![]() $l>0$
. For
$l>0$
. For
![]() $r\gg l$
, we have the following sequence of morphisms in
$r\gg l$
, we have the following sequence of morphisms in
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
:
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
:

where
![]() $P_{l}$
is the
$P_{l}$
is the
![]() $l$
th Postnikov filtration and
$l$
th Postnikov filtration and
![]() $\unicode[STIX]{x1D70F}_{{\leqslant}l}$
is the
$\unicode[STIX]{x1D70F}_{{\leqslant}l}$
is the
![]() $l$
th canonical filtration. According to Lemma 2.22, the composite
$l$
th canonical filtration. According to Lemma 2.22, the composite
![]() $\unicode[STIX]{x1D70F}_{{\leqslant}l}\mathsf{C}_{i}$
is independent of the choice of
$\unicode[STIX]{x1D70F}_{{\leqslant}l}\mathsf{C}_{i}$
is independent of the choice of
![]() $r$
. Also, the diagram
$r$
. Also, the diagram
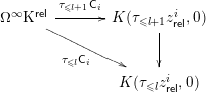
commutes, where the vertical map is the obvious one.
Theorem 2.26. Let
![]() $i>0$
. There exists a morphism
$i>0$
. There exists a morphism
in
![]() $\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. For
$\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. For
![]() $n\geqslant 0$
, its
$n\geqslant 0$
, its
![]() $(-n)$
th hypercohomology on a modulus pair
$(-n)$
th hypercohomology on a modulus pair
![]() $(X,D)$
yields a map
$(X,D)$
yields a map
which is functorial in
![]() $(X,D)\in \mathsf{MSm}$
and is a group homomorphism for
$(X,D)\in \mathsf{MSm}$
and is a group homomorphism for
![]() $n>0$
. This map coincides with Bloch’s Chern class [Reference BlochBl86, Section 7] when
$n>0$
. This map coincides with Bloch’s Chern class [Reference BlochBl86, Section 7] when
![]() $D=\emptyset$
.
$D=\emptyset$
.
Proof. We define ![]() . Since the Nisnevich cohomological dimension of
. Since the Nisnevich cohomological dimension of
![]() $X$
is finite, by taking the
$X$
is finite, by taking the
![]() $(-n)$
th hypercohomology of
$(-n)$
th hypercohomology of
![]() $\mathsf{C}_{i}$
, we obtain
$\mathsf{C}_{i}$
, we obtain
The first map is an isomorphism by Thomason–Trobaugh’s Nisnevich descent. Recall that
![]() $\mathsf{MSm}^{\ast }$
could be the category over any finite diagram in
$\mathsf{MSm}^{\ast }$
could be the category over any finite diagram in
![]() $\mathsf{MSm}$
, which ensures the functoriality. The map
$\mathsf{MSm}$
, which ensures the functoriality. The map
![]() $\mathsf{C}_{n,i}$
is a group homomorphism for
$\mathsf{C}_{n,i}$
is a group homomorphism for
![]() $n>0$
since it is defined by taking the
$n>0$
since it is defined by taking the
![]() $n$
th homotopy groups. Compatibility with Bloch’s Chern class is immediate from the construction.
$n$
th homotopy groups. Compatibility with Bloch’s Chern class is immediate from the construction.
3 Whitney sum formula
We show the Whitney sum formula for
![]() $\mathsf{C}_{0,\ast }$
by doing some more cycle computation. It involves the operation called algebraic join.
$\mathsf{C}_{0,\ast }$
by doing some more cycle computation. It involves the operation called algebraic join.
3.1 Algebraic join
Let
![]() $X$
be a scheme. Consider the projective spaces over
$X$
be a scheme. Consider the projective spaces over
![]() $X$
:
$X$
:
![]() $\mathbb{P}_{X}^{r-1}=\mathbf{Proj}({\mathcal{O}}_{X}[T_{1},\ldots ,T_{r}])$
,
$\mathbb{P}_{X}^{r-1}=\mathbf{Proj}({\mathcal{O}}_{X}[T_{1},\ldots ,T_{r}])$
,
![]() $\mathbb{P}_{X}^{s-1}=\mathbf{Proj}({\mathcal{O}}_{X}[T_{r+1},\ldots ,T_{r+s}])$
and
$\mathbb{P}_{X}^{s-1}=\mathbf{Proj}({\mathcal{O}}_{X}[T_{r+1},\ldots ,T_{r+s}])$
and
The schemes
![]() $\mathbb{P}_{X}^{r-1}$
and
$\mathbb{P}_{X}^{r-1}$
and
![]() $\mathbb{P}_{X}^{s-1}$
are naturally closed subschemes of
$\mathbb{P}_{X}^{s-1}$
are naturally closed subschemes of
![]() $\mathbb{P}_{X}^{r+s-1}$
. We consider the rational maps
$\mathbb{P}_{X}^{r+s-1}$
. We consider the rational maps
![]() $q_{1}\,:\,\mathbb{P}_{X}^{r+s-1}{\dashrightarrow}\mathbb{P}_{X}^{r-1}$
and
$q_{1}\,:\,\mathbb{P}_{X}^{r+s-1}{\dashrightarrow}\mathbb{P}_{X}^{r-1}$
and
![]() $q_{2}\,:\,\mathbb{P}_{X}^{r+s-1}{\dashrightarrow}\mathbb{P}_{X}^{s-1}$
defined by
$q_{2}\,:\,\mathbb{P}_{X}^{r+s-1}{\dashrightarrow}\mathbb{P}_{X}^{s-1}$
defined by
![]() $(T_{1},\ldots ,T_{r+s})\mapsto (T_{1},\ldots ,T_{r})$
and
$(T_{1},\ldots ,T_{r+s})\mapsto (T_{1},\ldots ,T_{r})$
and
![]() $\mapsto (T_{r+1},\ldots ,T_{r+s})$
.
$\mapsto (T_{r+1},\ldots ,T_{r+s})$
.
Denote by
![]() $\unicode[STIX]{x1D70B}_{1}\,:\,P_{1}\rightarrow \mathbb{P}_{X}^{r+s-1}$
the blow-up along the ill-defined locus
$\unicode[STIX]{x1D70B}_{1}\,:\,P_{1}\rightarrow \mathbb{P}_{X}^{r+s-1}$
the blow-up along the ill-defined locus
![]() $\mathbb{P}_{X}^{s-1}$
of
$\mathbb{P}_{X}^{s-1}$
of
![]() $q_{1}$
. Then
$q_{1}$
. Then
![]() $q_{1}$
induces a morphism
$q_{1}$
induces a morphism
![]() $q_{1}^{\prime }\,:\,P_{1}\rightarrow \mathbb{P}_{X}^{r-1}$
which is a
$q_{1}^{\prime }\,:\,P_{1}\rightarrow \mathbb{P}_{X}^{r-1}$
which is a
![]() $\mathbb{P}^{s}$
-bundle. Denote by
$\mathbb{P}^{s}$
-bundle. Denote by
![]() $q_{1}^{\ast }$
the operation on cycles defined as flat pull-back
$q_{1}^{\ast }$
the operation on cycles defined as flat pull-back
![]() $q_{1}^{\prime \ast }$
followed by proper push-forward
$q_{1}^{\prime \ast }$
followed by proper push-forward
![]() $\unicode[STIX]{x1D70B}_{1\ast }$
. Similarly, if
$\unicode[STIX]{x1D70B}_{1\ast }$
. Similarly, if
![]() $\unicode[STIX]{x1D70B}_{2}\,:\,P_{2}\rightarrow \mathbb{P}_{X}^{s-1}$
is the blow-up along
$\unicode[STIX]{x1D70B}_{2}\,:\,P_{2}\rightarrow \mathbb{P}_{X}^{s-1}$
is the blow-up along
![]() $\mathbb{P}_{X}^{r-1}$
, the rational map
$\mathbb{P}_{X}^{r-1}$
, the rational map
![]() $q_{2}$
induces a morphism
$q_{2}$
induces a morphism
![]() $q_{2}^{\prime }\,:\,P_{2}\rightarrow \mathbb{P}_{X}^{s-1}$
which is a
$q_{2}^{\prime }\,:\,P_{2}\rightarrow \mathbb{P}_{X}^{s-1}$
which is a
![]() $\mathbb{P}^{r}$
-bundle. Denote by
$\mathbb{P}^{r}$
-bundle. Denote by
![]() $q_{2}^{\ast }$
the flat pull-back
$q_{2}^{\ast }$
the flat pull-back
![]() $q_{2}^{\prime \ast }$
followed by push-forward
$q_{2}^{\prime \ast }$
followed by push-forward
![]() $\unicode[STIX]{x1D70B}_{2\ast }$
.
$\unicode[STIX]{x1D70B}_{2\ast }$
.
Observe the obvious fact that the cycle in
![]() $\mathbb{P}_{X}^{r-1}$
given by a set of homogeneous equations
$\mathbb{P}_{X}^{r-1}$
given by a set of homogeneous equations
![]() $\{f_{\unicode[STIX]{x1D6FC}}(T_{1},\ldots ,T_{r})\}_{\unicode[STIX]{x1D6FC}}$
is mapped by
$\{f_{\unicode[STIX]{x1D6FC}}(T_{1},\ldots ,T_{r})\}_{\unicode[STIX]{x1D6FC}}$
is mapped by
![]() $q_{1}^{\ast }$
to the cycle in
$q_{1}^{\ast }$
to the cycle in
![]() $\mathbb{P}_{X}^{r+s-1}$
defined by the same equations.
$\mathbb{P}_{X}^{r+s-1}$
defined by the same equations.
Lemma 3.1. Let
![]() $\unicode[STIX]{x1D6FC}$
be an element in
$\unicode[STIX]{x1D6FC}$
be an element in
![]() $z^{i}(\mathbb{P}_{X}^{r-1},m)$
and
$z^{i}(\mathbb{P}_{X}^{r-1},m)$
and
![]() $\unicode[STIX]{x1D6FD}$
be an element in
$\unicode[STIX]{x1D6FD}$
be an element in
![]() $z^{j}(\mathbb{P}_{X}^{r-1},n)$
. Suppose that the intersection product
$z^{j}(\mathbb{P}_{X}^{r-1},n)$
. Suppose that the intersection product
![]() $\unicode[STIX]{x1D6FC}\,\cdot \,\unicode[STIX]{x1D6FD}\in z^{i+j}(\mathbb{P}_{X}^{r-1},m+n)$
is defined. Then the same holds for cycles
$\unicode[STIX]{x1D6FC}\,\cdot \,\unicode[STIX]{x1D6FD}\in z^{i+j}(\mathbb{P}_{X}^{r-1},m+n)$
is defined. Then the same holds for cycles
![]() $q_{1}^{\ast }\unicode[STIX]{x1D6FC}\in z^{i}(\mathbb{P}_{X}^{r+s-1},m)$
and
$q_{1}^{\ast }\unicode[STIX]{x1D6FC}\in z^{i}(\mathbb{P}_{X}^{r+s-1},m)$
and
![]() $q_{1}^{\ast }\unicode[STIX]{x1D6FD}\in z^{j}(\mathbb{P}_{X}^{r+s-1},n)$
and we have an equality in
$q_{1}^{\ast }\unicode[STIX]{x1D6FD}\in z^{j}(\mathbb{P}_{X}^{r+s-1},n)$
and we have an equality in
![]() $z^{i+j}(\mathbb{P}_{X}^{r+s-1},m+n)$
:
$z^{i+j}(\mathbb{P}_{X}^{r+s-1},m+n)$
:
The same is true for the operation
![]() $q_{2}^{\ast }$
.
$q_{2}^{\ast }$
.
Proof. Preservation of intersection product certainly holds for flat pull-back. It holds for proper push-forward by birational maps
![]() $\unicode[STIX]{x1D70B}$
when the two cycles
$\unicode[STIX]{x1D70B}$
when the two cycles
![]() $\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime }$
under consideration satisfy:
$\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime }$
under consideration satisfy:
∙ The intersection product
 $(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FC}^{\prime })\,\cdot \,(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FD}^{\prime })$
is again defined, and
$(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FC}^{\prime })\,\cdot \,(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FD}^{\prime })$
is again defined, and∙ no component of
 $\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6FC}^{\prime }\,\cdot \,\unicode[STIX]{x1D6FD}^{\prime }$
or
$\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6FC}^{\prime }\,\cdot \,\unicode[STIX]{x1D6FD}^{\prime }$
or
 $(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FC}^{\prime })\,\cdot \,(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FD}^{\prime })$
is contained in the exceptional locus of
$(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FC}^{\prime })\,\cdot \,(\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FD}^{\prime })$
is contained in the exceptional locus of
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
This condition is satisfied in our case.
Definition 3.2. Let
![]() $\unicode[STIX]{x1D6FC}\in z^{i}(\mathbb{P}_{X}^{r-1},m)$
and
$\unicode[STIX]{x1D6FC}\in z^{i}(\mathbb{P}_{X}^{r-1},m)$
and
![]() $\unicode[STIX]{x1D6FD}\in z^{j}(\mathbb{P}_{X}^{s-1},n)$
be cycles. Consider the cycles
$\unicode[STIX]{x1D6FD}\in z^{j}(\mathbb{P}_{X}^{s-1},n)$
be cycles. Consider the cycles
![]() $q_{1}^{\ast }\unicode[STIX]{x1D6FC}\in z^{i}(\mathbb{P}_{X}^{r+s-1},m)$
and
$q_{1}^{\ast }\unicode[STIX]{x1D6FC}\in z^{i}(\mathbb{P}_{X}^{r+s-1},m)$
and
![]() $q_{2}^{\ast }\unicode[STIX]{x1D6FD}\in z^{j}(\mathbb{P}_{X}^{r+s-1},n)$
. When the intersection
$q_{2}^{\ast }\unicode[STIX]{x1D6FD}\in z^{j}(\mathbb{P}_{X}^{r+s-1},n)$
. When the intersection
![]() $(q_{1}^{\ast }\unicode[STIX]{x1D6FC})\,\cdot \,(q_{2}^{\ast }\unicode[STIX]{x1D6FD})\in z^{i+j}(\mathbb{P}_{X}^{r+s-1},m+n)$
is well defined, we denote it by
$(q_{1}^{\ast }\unicode[STIX]{x1D6FC})\,\cdot \,(q_{2}^{\ast }\unicode[STIX]{x1D6FD})\in z^{i+j}(\mathbb{P}_{X}^{r+s-1},m+n)$
is well defined, we denote it by
![]() $\unicode[STIX]{x1D6FC}\#\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FC}\#\unicode[STIX]{x1D6FD}$
.
The operation
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\mapsto \unicode[STIX]{x1D6FC}\#\unicode[STIX]{x1D6FD}$
is called algebraic join. It has been systematically used by authors like Friedlander, Lawson, Michelsohn and Walker. The authors of the present article learned this technique mainly in [Reference Friedlander and LawsonFL98].
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\mapsto \unicode[STIX]{x1D6FC}\#\unicode[STIX]{x1D6FD}$
is called algebraic join. It has been systematically used by authors like Friedlander, Lawson, Michelsohn and Walker. The authors of the present article learned this technique mainly in [Reference Friedlander and LawsonFL98].
3.2 The equalities
Let
![]() $r,s$
be non-negative integers. We keep the coordinate convention (10) when considering projective bundles
$r,s$
be non-negative integers. We keep the coordinate convention (10) when considering projective bundles
![]() $\mathbb{P}(E\text{GL}_{r})$
and
$\mathbb{P}(E\text{GL}_{r})$
and
![]() $\mathbb{P}(E\text{GL}_{s})$
. On the category
$\mathbb{P}(E\text{GL}_{s})$
. On the category
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
we consider presheaves:
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
we consider presheaves:
∙
 $p_{1\ast }z_{\mathsf{rel}}^{i}$
, which is induced from
$p_{1\ast }z_{\mathsf{rel}}^{i}$
, which is induced from
 $p_{\ast }z_{\mathsf{rel}}^{i}$
on
$p_{\ast }z_{\mathsf{rel}}^{i}$
on
 $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
by the first projection
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
by the first projection
 $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}\rightarrow \boldsymbol{X}_{r}^{\mathsf{rel}}$
;
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}\rightarrow \boldsymbol{X}_{r}^{\mathsf{rel}}$
;∙
 $p_{2\ast }z_{\mathsf{rel}}^{i}$
, induced by the second projection
$p_{2\ast }z_{\mathsf{rel}}^{i}$
, induced by the second projection
 $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}\rightarrow \boldsymbol{X}_{s}^{\mathsf{rel}}$
;
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}\rightarrow \boldsymbol{X}_{s}^{\mathsf{rel}}$
;∙
 $p_{\ast }z_{\mathsf{rel}}^{i}$
, induced by the inclusion
$p_{\ast }z_{\mathsf{rel}}^{i}$
, induced by the inclusion
 $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}{\hookrightarrow}\boldsymbol{X}_{r+s}^{\,\mathsf{rel}}$
;
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}{\hookrightarrow}\boldsymbol{X}_{r+s}^{\,\mathsf{rel}}$
;∙ their nonmodulus counterparts
 $p_{1\ast }z^{i}$
,
$p_{1\ast }z^{i}$
,
 $p_{2\ast }z^{i}$
and
$p_{2\ast }z^{i}$
and
 $p_{\ast }z^{i}$
.
$p_{\ast }z^{i}$
.
Let us distinguish the pull-back maps by writing
![]() $p_{1}^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{1\ast }z_{\mathsf{rel}}^{i}$
,
$p_{1}^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{1\ast }z_{\mathsf{rel}}^{i}$
,
![]() $p_{2}^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{2\ast }z_{\mathsf{rel}}^{i}$
and
$p_{2}^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{2\ast }z_{\mathsf{rel}}^{i}$
and
![]() $p^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}$
. Similarly, we can consider three different versions of
$p^{\ast }\,:\,z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}$
. Similarly, we can consider three different versions of
![]() ${\mathcal{Z}}$
’s, denoted by
${\mathcal{Z}}$
’s, denoted by
![]() ${\mathcal{Z}}_{1}$
,
${\mathcal{Z}}_{1}$
,
![]() ${\mathcal{Z}}_{2}$
and
${\mathcal{Z}}_{2}$
and
![]() ${\mathcal{Z}}$
. There are obvious maps
${\mathcal{Z}}$
. There are obvious maps
![]() ${\mathcal{Z}}\rightarrow {\mathcal{Z}}_{1}$
and
${\mathcal{Z}}\rightarrow {\mathcal{Z}}_{1}$
and
![]() ${\mathcal{Z}}\rightarrow {\mathcal{Z}}_{2}$
.
${\mathcal{Z}}\rightarrow {\mathcal{Z}}_{2}$
.
We may consider the partially defined join operator
![]() $\#\,:\,p_{1\ast }z_{\mathsf{rel}}^{i}\otimes p_{2\ast }z_{\mathsf{rel}}^{j}{\dashrightarrow}p_{\ast }z_{\mathsf{rel}}^{i+j}$
and its nonmodulus version. The modulus version is a well-defined map in
$\#\,:\,p_{1\ast }z_{\mathsf{rel}}^{i}\otimes p_{2\ast }z_{\mathsf{rel}}^{j}{\dashrightarrow}p_{\ast }z_{\mathsf{rel}}^{i+j}$
and its nonmodulus version. The modulus version is a well-defined map in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
(Section B.1.2). Given two maps
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
(Section B.1.2). Given two maps
![]() $\unicode[STIX]{x1D6FC}\,:\,{\mathcal{Z}}\rightarrow p_{1\ast }z^{i}$
and
$\unicode[STIX]{x1D6FC}\,:\,{\mathcal{Z}}\rightarrow p_{1\ast }z^{i}$
and
![]() $\unicode[STIX]{x1D6FD}\,:\,{\mathcal{Z}}\rightarrow p_{2\ast }z^{j}$
, we consider their cup product followed by algebraic join to get a map
$\unicode[STIX]{x1D6FD}\,:\,{\mathcal{Z}}\rightarrow p_{2\ast }z^{j}$
, we consider their cup product followed by algebraic join to get a map
![]() $\unicode[STIX]{x1D6FC}\#\unicode[STIX]{x1D6FD}\,:\,{\mathcal{Z}}\rightarrow p_{\ast }z^{i+j}$
whenever it is well defined.
$\unicode[STIX]{x1D6FC}\#\unicode[STIX]{x1D6FD}\,:\,{\mathcal{Z}}\rightarrow p_{\ast }z^{i+j}$
whenever it is well defined.
In Remark 2.19 (ii), we defined maps
![]() $C_{\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}}^{i}$
of presheaves on
$C_{\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}}^{i}$
of presheaves on
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
. Via
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}$
. Via
![]() ${\mathcal{Z}}\rightarrow {\mathcal{Z}}_{1}$
, it induces a map
${\mathcal{Z}}\rightarrow {\mathcal{Z}}_{1}$
, it induces a map
which we denote by the same symbol. Similarly for
![]() $C_{\mathsf{MSm}^{\ast }/\boldsymbol{X}_{s}^{\mathsf{rel}}}^{j}$
. Recall that they depend on the choice of
$C_{\mathsf{MSm}^{\ast }/\boldsymbol{X}_{s}^{\mathsf{rel}}}^{j}$
. Recall that they depend on the choice of
![]() $i$
indices out of
$i$
indices out of
![]() $\{1,\ldots ,r\}$
and
$\{1,\ldots ,r\}$
and
![]() $j$
out of
$j$
out of
![]() $\{r+1,\ldots ,r+s\}$
although it is not explicit in the notation.
$\{r+1,\ldots ,r+s\}$
although it is not explicit in the notation.
Also, thanks to Remark 2.19 (i)(ii), we have yet other maps
for integers
![]() $1\leqslant k\leqslant r+s$
.
$1\leqslant k\leqslant r+s$
.
Proposition 3.3. For any
![]() $0\leqslant i\leqslant r$
and
$0\leqslant i\leqslant r$
and
![]() $0\leqslant j\leqslant s$
, the two maps
$0\leqslant j\leqslant s$
, the two maps
are equal as maps of presheaves on
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
under appropriate choices of indices (specified in the proof). In particular we have
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}$
under appropriate choices of indices (specified in the proof). In particular we have
![]() $\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}\#\unicode[STIX]{x1D709}_{\mathsf{rel}}^{s}=\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r+s}$
as maps
$\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}\#\unicode[STIX]{x1D709}_{\mathsf{rel}}^{s}=\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r+s}$
as maps
![]() $\mathbb{Z}\rightrightarrows p_{\ast }z_{\mathsf{rel}}^{r+s}$
in
$\mathbb{Z}\rightrightarrows p_{\ast }z_{\mathsf{rel}}^{r+s}$
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
.
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
.
Proof. It suffices to prove the corresponding equality of cycles on the simplicial scheme
![]() $\mathbb{P}(E\text{GL}_{r+s})_{|B\text{GL}_{r}\times B\text{GL}_{s}}$
. By the definition of algebraic join of maps, the problem is to prove the equality of maps:
$\mathbb{P}(E\text{GL}_{r+s})_{|B\text{GL}_{r}\times B\text{GL}_{s}}$
. By the definition of algebraic join of maps, the problem is to prove the equality of maps:
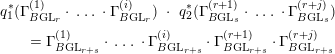 $$\begin{eqnarray}\displaystyle & & \displaystyle q_{1}^{\ast }(\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r}}^{(1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r}}^{(i)})~\,\cdot \,~q_{2}^{\ast }(\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{s}}^{(r+1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{s}}^{(r+j)})\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(i)}\,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(r+1)}\,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(r+j)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle q_{1}^{\ast }(\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r}}^{(1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r}}^{(i)})~\,\cdot \,~q_{2}^{\ast }(\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{s}}^{(r+1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{s}}^{(r+j)})\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(1)}\,\cdot \,\ldots \,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(i)}\,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(r+1)}\,\cdot \,\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(r+j)}\nonumber\end{eqnarray}$$
from the cone of
to
![]() $z^{r+s}(\mathbb{P}_{k(\text{GL}_{r}\times \text{GL}_{s})}^{r+s-1}\times -,\bullet )$
. By Lemma 3.1, it is reduced to the equalities of cycles
$z^{r+s}(\mathbb{P}_{k(\text{GL}_{r}\times \text{GL}_{s})}^{r+s-1}\times -,\bullet )$
. By Lemma 3.1, it is reduced to the equalities of cycles
![]() $q_{1}^{\ast }\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r}}^{(a)\ast }(S)=\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(a)\ast }(S)$
on
$q_{1}^{\ast }\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r}}^{(a)\ast }(S)=\unicode[STIX]{x1D6E4}\text{}_{B\text{GL}_{r+s}}^{(a)\ast }(S)$
on
![]() $\mathbb{P}(E_{n}\text{GL}_{r+s})_{|B\text{GL}_{r}^{\ast }\times B\text{GL}_{s}^{\ast }}$
for all
$\mathbb{P}(E_{n}\text{GL}_{r+s})_{|B\text{GL}_{r}^{\ast }\times B\text{GL}_{s}^{\ast }}$
for all
![]() $1\leqslant a\leqslant r$
and nonempty subsets
$1\leqslant a\leqslant r$
and nonempty subsets
![]() $S\subset [n]$
, and its variants involving
$S\subset [n]$
, and its variants involving
![]() $\circ$
,
$\circ$
,
![]() $\circ \ast$
and
$\circ \ast$
and
![]() $q_{2}^{\ast }$
. In view of the fact observed before Lemma 3.1, this last equality clearly holds. This completes the proof of the proposition.
$q_{2}^{\ast }$
. In view of the fact observed before Lemma 3.1, this last equality clearly holds. This completes the proof of the proposition.
Now, consider the following diagram in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
(see Sections B.1.1, B.1.2 for the tensor products
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
(see Sections B.1.1, B.1.2 for the tensor products
![]() $\overset{\text{:D}}{\otimes }$
):
$\overset{\text{:D}}{\otimes }$
):
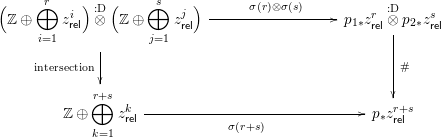
where the vertical map “intersection” sends an element
![]() $(\unicode[STIX]{x1D6FC}_{0},(\unicode[STIX]{x1D6FC}_{i})_{i})\otimes (\unicode[STIX]{x1D6FD}_{0},(\unicode[STIX]{x1D6FD}_{j})_{j})$
to the tuple of cycles
$(\unicode[STIX]{x1D6FC}_{0},(\unicode[STIX]{x1D6FC}_{i})_{i})\otimes (\unicode[STIX]{x1D6FD}_{0},(\unicode[STIX]{x1D6FD}_{j})_{j})$
to the tuple of cycles
![]() $(\sum _{k=i+j}\unicode[STIX]{x1D6FC}_{i}\,\cdot \,\unicode[STIX]{x1D6FD}_{j})_{0\leqslant k\leqslant r+s}$
. The horizontal maps
$(\sum _{k=i+j}\unicode[STIX]{x1D6FC}_{i}\,\cdot \,\unicode[STIX]{x1D6FD}_{j})_{0\leqslant k\leqslant r+s}$
. The horizontal maps
![]() $\unicode[STIX]{x1D70E}$
are defined by
$\unicode[STIX]{x1D70E}$
are defined by
![]() $\unicode[STIX]{x1D70E}(r)\,:\,(\unicode[STIX]{x1D6FC}_{0},(\unicode[STIX]{x1D6FC}_{i})_{i=1}^{r})\mapsto \unicode[STIX]{x1D6FC}_{0}\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}+\sum _{i=1}^{r}p^{\ast }(\unicode[STIX]{x1D6FC}_{i})\,\cdot \,\unicode[STIX]{x1D709}^{r-i}.$
Applying Lemma 3.1, Proposition 3.3 and the commutativity of intersection product in the derived category, one checks that the diagram (11) commutes.
$\unicode[STIX]{x1D70E}(r)\,:\,(\unicode[STIX]{x1D6FC}_{0},(\unicode[STIX]{x1D6FC}_{i})_{i=1}^{r})\mapsto \unicode[STIX]{x1D6FC}_{0}\unicode[STIX]{x1D709}_{\mathsf{rel}}^{r}+\sum _{i=1}^{r}p^{\ast }(\unicode[STIX]{x1D6FC}_{i})\,\cdot \,\unicode[STIX]{x1D709}^{r-i}.$
Applying Lemma 3.1, Proposition 3.3 and the commutativity of intersection product in the derived category, one checks that the diagram (11) commutes.
The rank
![]() $r$
Chern classes
$r$
Chern classes
![]() $c_{i}$
are characterized by the property that the composite map
$c_{i}$
are characterized by the property that the composite map
![]() $\mathbb{Z}\xrightarrow[{}]{(1,c_{1},\ldots ,c_{r})}\mathbb{Z}\oplus \bigoplus _{i=1}^{r}z_{\mathsf{rel}}^{i}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}p_{\ast }z_{\mathsf{rel}}^{r}$
is zero. Of course the same holds for the rank
$\mathbb{Z}\xrightarrow[{}]{(1,c_{1},\ldots ,c_{r})}\mathbb{Z}\oplus \bigoplus _{i=1}^{r}z_{\mathsf{rel}}^{i}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}p_{\ast }z_{\mathsf{rel}}^{r}$
is zero. Of course the same holds for the rank
![]() $s$
case. It follows by the commutativity of (11) that the composite
$s$
case. It follows by the commutativity of (11) that the composite
![]() $\mathbb{Z}\xrightarrow[{}]{(\sum _{i+j=k}c_{i}\,\cdot \,c_{j})_{k\geqslant 0}}\mathbb{Z}\oplus \bigoplus _{k=1}^{r+s}z_{\mathsf{rel}}^{k}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}p_{\ast }z_{\mathsf{rel}}^{r+s}$
is zero. From the characterization of Chern classes we get:
$\mathbb{Z}\xrightarrow[{}]{(\sum _{i+j=k}c_{i}\,\cdot \,c_{j})_{k\geqslant 0}}\mathbb{Z}\oplus \bigoplus _{k=1}^{r+s}z_{\mathsf{rel}}^{k}\xrightarrow[{}]{\unicode[STIX]{x1D70E}}p_{\ast }z_{\mathsf{rel}}^{r+s}$
is zero. From the characterization of Chern classes we get:
Proposition 3.4. We have an equality
![]() $c_{k}=\sum _{i+j=k}c_{i}\,\cdot \,c_{j}$
(where
$c_{k}=\sum _{i+j=k}c_{i}\,\cdot \,c_{j}$
(where
![]() $c_{0}:=1$
) of maps
$c_{0}:=1$
) of maps
![]() $\mathbb{Z}\rightrightarrows z_{\mathsf{rel}}^{k}$
in
$\mathbb{Z}\rightrightarrows z_{\mathsf{rel}}^{k}$
in
![]() $D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
for
$D(\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}})$
for
![]() $1\leqslant k\leqslant r+s$
.
$1\leqslant k\leqslant r+s$
.
Equivalently, it is an equality of maps
![]() $\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}\rightrightarrows K(z_{\mathsf{rel}}^{k},0)$
in the homotopy category of pointed simplicial presheaves
$\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{s}^{\mathsf{rel}}\rightrightarrows K(z_{\mathsf{rel}}^{k},0)$
in the homotopy category of pointed simplicial presheaves
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
.
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
.
Corollary 3.5. The diagram in
![]() $\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
$\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$

is commutative, where the left vertical map is defined by the diagonal sum of matrices and the right one is defined by the intersection product.
3.3 Whitney sum formula on the relative
 $K$
-theory
$K$
-theory
We set
![]() $\tilde{z}_{\mathsf{rel}}^{\ast }:=\mathbb{Z}\oplus (\bigoplus _{i\geqslant 1}z_{\mathsf{rel}}^{i})$
. We define the total Chern class map
$\tilde{z}_{\mathsf{rel}}^{\ast }:=\mathbb{Z}\oplus (\bigoplus _{i\geqslant 1}z_{\mathsf{rel}}^{i})$
. We define the total Chern class map
by the product of the canonical map
![]() $\mathbb{Z}^{\mathsf{rel}}\rightarrow \mathbb{Z}$
and
$\mathbb{Z}^{\mathsf{rel}}\rightarrow \mathbb{Z}$
and
![]() $(1,\mathsf{C}_{1},\mathsf{C}_{2},\ldots \,\!)$
. We have seen that the diagonal sum of
$(1,\mathsf{C}_{1},\mathsf{C}_{2},\ldots \,\!)$
. We have seen that the diagonal sum of
![]() $\boldsymbol{X}^{\mathsf{rel}}$
and the group law of
$\boldsymbol{X}^{\mathsf{rel}}$
and the group law of
![]() $\mathbb{Z}^{\mathsf{rel}}$
is compatible with the loop composition of
$\mathbb{Z}^{\mathsf{rel}}$
is compatible with the loop composition of
![]() $\unicode[STIX]{x1D6FA}^{\infty }\text{K}^{\mathsf{rel}}$
(Theorem 2.24). It follows from Corollary 3.5 that the diagram in
$\unicode[STIX]{x1D6FA}^{\infty }\text{K}^{\mathsf{rel}}$
(Theorem 2.24). It follows from Corollary 3.5 that the diagram in
![]() $\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
$\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$

is commutative. By taking the
![]() $0$
th hypercohomology of
$0$
th hypercohomology of
![]() $\mathsf{C}_{\mathsf{tot}}$
on a modulus pair
$\mathsf{C}_{\mathsf{tot}}$
on a modulus pair
![]() $(X,D)$
, we obtain a map
$(X,D)$
, we obtain a map
We regard the target as a group by
It follows from the above commutative diagram that:
Theorem 3.6. The map (13) is a group homomorphism. In other words, we have
for
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \text{K}_{0}(X,D)$
with the convention
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \text{K}_{0}(X,D)$
with the convention
![]() $\mathsf{C}_{0,0}=1$
.
$\mathsf{C}_{0,0}=1$
.
4 Chern character and application
4.1 Chern character
We set
where the Hom group is taken in the category
![]() $\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. Under this convention, the total Chern class (12) is in the set
$\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. Under this convention, the total Chern class (12) is in the set
![]() $A^{0}\times \{1\}\times \prod _{i\geqslant 1}A^{i}$
. We define a map
$A^{0}\times \{1\}\times \prod _{i\geqslant 1}A^{i}$
. We define a map
as in [Reference Berthelot, Grothendieck and IllusieSGA6, Exposé 0, Appendix 1.26], that is,
where
![]() $\unicode[STIX]{x1D702}$
is an endomorphism of
$\unicode[STIX]{x1D702}$
is an endomorphism of
![]() $A_{\mathbb{Q}}^{\ast }$
defined by
$A_{\mathbb{Q}}^{\ast }$
defined by
![]() $\unicode[STIX]{x1D702}(x^{i})=(-1)^{i-1}x^{i}/(i-1)!$
.
$\unicode[STIX]{x1D702}(x^{i})=(-1)^{i-1}x^{i}/(i-1)!$
.
The image of
![]() $\mathsf{C}_{\mathsf{tot}}$
by
$\mathsf{C}_{\mathsf{tot}}$
by
![]() $\text{ch}$
gives a map
$\text{ch}$
gives a map
in
![]() $\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. According to Theorems 2.26 and 3.6, we obtain the following result.
$\text{pro}-\mathsf{Ho}(s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))$
. According to Theorems 2.26 and 3.6, we obtain the following result.
Theorem 4.1. Let
![]() $(X,D)\in \mathsf{MSm}$
and
$(X,D)\in \mathsf{MSm}$
and
![]() $n\geqslant 0$
. The
$n\geqslant 0$
. The
![]() $(-n)$
th hypercohomology of (14) yields a group homomorphism
$(-n)$
th hypercohomology of (14) yields a group homomorphism
which is functorial in
![]() $(X,D)$
and coincides with Bloch’s Chern character when
$(X,D)$
and coincides with Bloch’s Chern character when
![]() $D=\emptyset$
.
$D=\emptyset$
.
For an additive category
![]() ${\mathcal{A}}$
, let
${\mathcal{A}}$
, let
![]() ${\mathcal{A}}_{\mathbb{Q}}$
be the category up to isogeny, which has the same objects as
${\mathcal{A}}_{\mathbb{Q}}$
be the category up to isogeny, which has the same objects as
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() $\operatorname{Hom}_{{\mathcal{A}}_{\mathbb{Q}}}(M,N)=\operatorname{Hom}_{{\mathcal{A}}}(M,N)\otimes \mathbb{Q}$
. We denote the image of
$\operatorname{Hom}_{{\mathcal{A}}_{\mathbb{Q}}}(M,N)=\operatorname{Hom}_{{\mathcal{A}}}(M,N)\otimes \mathbb{Q}$
. We denote the image of
![]() $M\in {\mathcal{A}}$
in
$M\in {\mathcal{A}}$
in
![]() ${\mathcal{A}}_{\mathbb{Q}}$
by
${\mathcal{A}}_{\mathbb{Q}}$
by
![]() $M_{\mathbb{Q}}$
.
$M_{\mathbb{Q}}$
.
For a presheaf
![]() $F$
on
$F$
on
![]() $\mathsf{MSm}$
, we define a pro-system of presheaves
$\mathsf{MSm}$
, we define a pro-system of presheaves
![]() $\hat{F}$
by
$\hat{F}$
by
The above argument can be modified to obtain a map
in
![]() $\text{pro}-\mathsf{Ho}(\text{pro}-s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))_{\mathbb{Q}}$
. Here is a variant of Theorem 4.1.
$\text{pro}-\mathsf{Ho}(\text{pro}-s\mathsf{PSh}_{\ast }(\mathsf{MSm}^{\ast }))_{\mathbb{Q}}$
. Here is a variant of Theorem 4.1.
Theorem 4.2. Let
![]() $(X,D)\in \mathsf{MSm}$
and
$(X,D)\in \mathsf{MSm}$
and
![]() $n\geqslant 0$
. The
$n\geqslant 0$
. The
![]() $(-n)$
th hypercohomology of (15) yields a morphism
$(-n)$
th hypercohomology of (15) yields a morphism
in the category of pro-abelian groups
![]() $(\text{pro}-\mathsf{Ab})_{\mathbb{Q}}$
up to isogeny. This is functorial in
$(\text{pro}-\mathsf{Ab})_{\mathbb{Q}}$
up to isogeny. This is functorial in
![]() $(X,D)$
and coincides with Bloch’s Chern character when
$(X,D)$
and coincides with Bloch’s Chern character when
![]() $D=\emptyset$
.
$D=\emptyset$
.
4.2 Relative motivic cohomology of henselian dvr
Let
![]() $k$
be a field of characteristic zero. Let
$k$
be a field of characteristic zero. Let
![]() $A$
be a henselian dvr over
$A$
be a henselian dvr over
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D70B}$
its uniformizer. Set
$\unicode[STIX]{x1D70B}$
its uniformizer. Set
![]() $X=\text{Spec}A$
and
$X=\text{Spec}A$
and
![]() $D=\text{Spec}A/\unicode[STIX]{x1D70B}$
. In this section, we prove the following.
$D=\text{Spec}A/\unicode[STIX]{x1D70B}$
. In this section, we prove the following.
Theorem 4.3. For every
![]() $n\geqslant 0$
, there is a natural isomorphism
$n\geqslant 0$
, there is a natural isomorphism
in the category
![]() $(\text{pro}-\mathsf{Ab})_{\mathbb{Q}}$
of pro-abelian groups up to isogeny.
$(\text{pro}-\mathsf{Ab})_{\mathbb{Q}}$
of pro-abelian groups up to isogeny.
We expect that
![]() $\{\ker (\text{CH}^{i}(X|mD,n)\rightarrow \text{CH}^{i}(X,n))\}_{m,\mathbb{Q}}$
vanishes.
$\{\ker (\text{CH}^{i}(X|mD,n)\rightarrow \text{CH}^{i}(X,n))\}_{m,\mathbb{Q}}$
vanishes.
Lemma 4.4. The canonical map
is a pro-epimorphism.
Proof. By Artin’s approximation theorem [Reference ArtinAr69], we may replace
![]() $A$
by its completion
$A$
by its completion
![]() $\hat{A}\simeq F[[t]]$
, that is, enough to show that
$\hat{A}\simeq F[[t]]$
, that is, enough to show that
is a pro-epimorphism.
Since
![]() $\text{K}_{n}(F[[t]])\rightarrow \text{K}_{n}(F)$
is a split surjection, it suffices to show that
$\text{K}_{n}(F[[t]])\rightarrow \text{K}_{n}(F)$
is a split surjection, it suffices to show that
is a pro-epimorphism. By Goodwillie’s theorem [Reference GoodwillieGo86] and the
![]() $\operatorname{HC}$
version of pro HKR theorem [Reference MorrowMo15, Theorem 3.23], we have pro-isomorphisms
$\operatorname{HC}$
version of pro HKR theorem [Reference MorrowMo15, Theorem 3.23], we have pro-isomorphisms
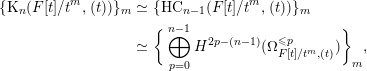 $$\begin{eqnarray}\displaystyle \{\text{K}_{n}(F[t]/t^{m},(t))\}_{m} & \simeq & \displaystyle \{\operatorname{HC}_{n-1}(F[t]/t^{m},(t))\}_{m}\nonumber\\ \displaystyle & \simeq & \displaystyle \bigg\{\bigoplus _{p=0}^{n-1}H^{2p-(n-1)}(\unicode[STIX]{x1D6FA}_{F[t]/t^{m},(t)}^{{\leqslant}p})\bigg\}_{m},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{\text{K}_{n}(F[t]/t^{m},(t))\}_{m} & \simeq & \displaystyle \{\operatorname{HC}_{n-1}(F[t]/t^{m},(t))\}_{m}\nonumber\\ \displaystyle & \simeq & \displaystyle \bigg\{\bigoplus _{p=0}^{n-1}H^{2p-(n-1)}(\unicode[STIX]{x1D6FA}_{F[t]/t^{m},(t)}^{{\leqslant}p})\bigg\}_{m},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FA}_{A,I}^{j}:=\ker (\unicode[STIX]{x1D6FA}_{A}^{j}\rightarrow \unicode[STIX]{x1D6FA}_{A/I}^{j})$
. By the Poincaré lemma [Reference WeibelWei94, Corollary 9.9.3], we have
$\unicode[STIX]{x1D6FA}_{A,I}^{j}:=\ker (\unicode[STIX]{x1D6FA}_{A}^{j}\rightarrow \unicode[STIX]{x1D6FA}_{A/I}^{j})$
. By the Poincaré lemma [Reference WeibelWei94, Corollary 9.9.3], we have
for every
![]() $m,j\geqslant 0$
. Hence, it follows that
$m,j\geqslant 0$
. Hence, it follows that
Consider the commutative diagram

where the rows are exact and the vertical maps are split surjections. Again by the Poincaré lemma, the left vertical map is an isomorphism, and thus we have an isomorphism
Given an element
![]() $f\otimes d\log y_{1}\wedge \cdots \wedge d\log y_{n-1}\in tF[t]/t^{m}\otimes _{F}\unicode[STIX]{x1D6FA}_{F}^{n-1}$
, the element
$f\otimes d\log y_{1}\wedge \cdots \wedge d\log y_{n-1}\in tF[t]/t^{m}\otimes _{F}\unicode[STIX]{x1D6FA}_{F}^{n-1}$
, the element
![]() $\{\exp (f),y_{1},\ldots ,y_{n-1}\}\in \text{K}_{n}^{M}(F[[t]])$
lifts it via
$\{\exp (f),y_{1},\ldots ,y_{n-1}\}\in \text{K}_{n}^{M}(F[[t]])$
lifts it via
Therefore, the composite
is isomorphic to a levelwise epimorphism, and thus the first map is a pro-epimorphism. This proves the lemma.
Proof of Theorem 4.3.
The Chern character
![]() $\hat{\mathsf{ch}}_{n}$
in Theorem 4.2 fits into the commutative diagram
$\hat{\mathsf{ch}}_{n}$
in Theorem 4.2 fits into the commutative diagram

in
![]() $(\text{pro}-\mathsf{An})_{\mathbb{Q}}$
. By Lemma 4.4, the upper sequence is exact. By Bloch’s comparison theorem in [Reference BlochBl86], the middle vertical map
$(\text{pro}-\mathsf{An})_{\mathbb{Q}}$
. By Lemma 4.4, the upper sequence is exact. By Bloch’s comparison theorem in [Reference BlochBl86], the middle vertical map
![]() $\mathsf{ch}_{n}$
is an isomorphism. Hence, it follows that the left vertical map
$\mathsf{ch}_{n}$
is an isomorphism. Hence, it follows that the left vertical map
![]() $\hat{\mathsf{ch}}_{n}$
is a pro-monomorphism.
$\hat{\mathsf{ch}}_{n}$
is a pro-monomorphism.
We shall show that the composite
is the zero map.
Binda–Saito [Reference Binda and SaitoBS17] has constructed the cycle map
where
![]() $\unicode[STIX]{x1D6FA}_{X|mD}^{j}=\unicode[STIX]{x1D6FA}_{A}^{j}(\log D)\otimes A\unicode[STIX]{x1D70B}^{m}$
. Note that we have a pro-isomorphism
$\unicode[STIX]{x1D6FA}_{X|mD}^{j}=\unicode[STIX]{x1D6FA}_{A}^{j}(\log D)\otimes A\unicode[STIX]{x1D70B}^{m}$
. Note that we have a pro-isomorphism
![]() ${\{\unicode[STIX]{x1D6FA}_{X|mD}^{j}\}}_{m}\simeq {\{\unicode[STIX]{x1D6FA}_{A}^{j}\otimes A\unicode[STIX]{x1D70B}^{m}\}}_{m}$
. Hence, we have a commutative diagram
${\{\unicode[STIX]{x1D6FA}_{X|mD}^{j}\}}_{m}\simeq {\{\unicode[STIX]{x1D6FA}_{A}^{j}\otimes A\unicode[STIX]{x1D70B}^{m}\}}_{m}$
. Hence, we have a commutative diagram

and the bottom composite is zero. Here, the second vertical map is the usual cycle map to the de Rham cohomology, and the composite
coincides with Goodwillie’s Chern character by [Reference WeibelWei93]. Therefore, the composite
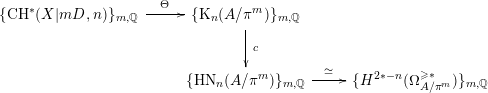
equals zero, where
![]() $c$
is Goodwillie’s Chern character and the last isomorphism is by the pro HKR theorem again. (The pro HKR theorem may not yield a pro-isomorphism for
$c$
is Goodwillie’s Chern character and the last isomorphism is by the pro HKR theorem again. (The pro HKR theorem may not yield a pro-isomorphism for
![]() $\operatorname{HN}$
in general, but now the relative part
$\operatorname{HN}$
in general, but now the relative part
![]() $\operatorname{HN}_{n}(A/\unicode[STIX]{x1D70B}^{m},(\unicode[STIX]{x1D70B}))$
is equal to
$\operatorname{HN}_{n}(A/\unicode[STIX]{x1D70B}^{m},(\unicode[STIX]{x1D70B}))$
is equal to
![]() $\operatorname{HC}_{n-1}(A/\unicode[STIX]{x1D70B}^{m},(\unicode[STIX]{x1D70B}))$
for which we can apply the pro HKR theorem, and we obtain the above pro-isomorphism by the five lemma.)
$\operatorname{HC}_{n-1}(A/\unicode[STIX]{x1D70B}^{m},(\unicode[STIX]{x1D70B}))$
for which we can apply the pro HKR theorem, and we obtain the above pro-isomorphism by the five lemma.)
Consider the commutative diagram
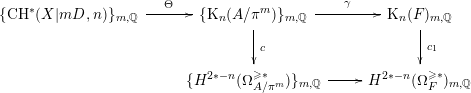
where
![]() $c$
and
$c$
and
![]() $c_{1}$
are Goodwillie’s Chern characters and
$c_{1}$
are Goodwillie’s Chern characters and
![]() $\unicode[STIX]{x1D6FE}$
is the canonical map. We have seen that
$\unicode[STIX]{x1D6FE}$
is the canonical map. We have seen that
![]() $c\circ \unicode[STIX]{x1D6E9}=0$
, and it is clear that
$c\circ \unicode[STIX]{x1D6E9}=0$
, and it is clear that
![]() $\unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D6E9}=0$
. We claim that the kernels of
$\unicode[STIX]{x1D6FE}\circ \unicode[STIX]{x1D6E9}=0$
. We claim that the kernels of
![]() $c$
and
$c$
and
![]() $c_{1}$
are isomorphic, which implies that
$c_{1}$
are isomorphic, which implies that
![]() $\unicode[STIX]{x1D6E9}=0$
. Indeed, the above square fits into the diagram
$\unicode[STIX]{x1D6E9}=0$
. Indeed, the above square fits into the diagram
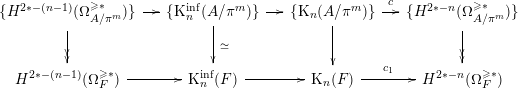
with exact rows. Here, the first vertical map is surjective and the second vertical map is an isomorphism by Goodwillie’s theorem [Reference GoodwillieGo86]. Hence,
![]() $\ker c\simeq \ker c_{1}$
follows.
$\ker c\simeq \ker c_{1}$
follows.
Consequently, we obtain a morphism
It is clear that
![]() $\unicode[STIX]{x1D719}\circ \hat{\mathsf{ch}}_{n}=\text{id}$
and that
$\unicode[STIX]{x1D719}\circ \hat{\mathsf{ch}}_{n}=\text{id}$
and that
![]() $\unicode[STIX]{x1D6FC}\circ \hat{\mathsf{ch}}_{n}\circ \unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FC}$
. This completes the proof of Theorem 4.3.
$\unicode[STIX]{x1D6FC}\circ \hat{\mathsf{ch}}_{n}\circ \unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FC}$
. This completes the proof of Theorem 4.3.
Acknowledgments
When the authors were graduate students, Shuji Saito, Kanetomo Sato and Kei Hagihara encouraged the authors to learn
![]() $K$
-theory techniques like the Volodin space and stability results, and moving techniques of algebraic cycles, which later turned out indispensable in carrying out this project. Part of the work was done while one or both of the authors were staying at the Universität Regensburg on several occasions. Conversations with Federico Binda and Hiroyasu Miyazaki were helpful. We owe a lot to the referee for improvement in exposition. The work was supported by JSPS KAKENHI Grant Number 15J02264, 16J08843, and by the Program for Leading Graduate Schools, MEXT, Japan.
$K$
-theory techniques like the Volodin space and stability results, and moving techniques of algebraic cycles, which later turned out indispensable in carrying out this project. Part of the work was done while one or both of the authors were staying at the Universität Regensburg on several occasions. Conversations with Federico Binda and Hiroyasu Miyazaki were helpful. We owe a lot to the referee for improvement in exposition. The work was supported by JSPS KAKENHI Grant Number 15J02264, 16J08843, and by the Program for Leading Graduate Schools, MEXT, Japan.
Appendix A. A lemma on local homotopy theory
The goal in this section is to prove Theorem A.5. We fix a small site
![]() ${\mathcal{C}}$
. We denote by
${\mathcal{C}}$
. We denote by
![]() $\mathsf{PSh}({\mathcal{C}})$
(resp.
$\mathsf{PSh}({\mathcal{C}})$
(resp.
![]() $s\mathsf{PSh}({\mathcal{C}})$
) the category of presheaves (resp. simplicial presheaves) on
$s\mathsf{PSh}({\mathcal{C}})$
) the category of presheaves (resp. simplicial presheaves) on
![]() ${\mathcal{C}}$
. We endow
${\mathcal{C}}$
. We endow
![]() $s\mathsf{PSh}({\mathcal{C}})$
with the local injective model structure, cf. [Reference JardineJar15, Theorem 5.8]. Let us begin with a general construction:
$s\mathsf{PSh}({\mathcal{C}})$
with the local injective model structure, cf. [Reference JardineJar15, Theorem 5.8]. Let us begin with a general construction:
Definition A.1. Let
![]() $F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{PSh}({\mathcal{C}})$
be a functor with
$F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{PSh}({\mathcal{C}})$
be a functor with
![]() $\unicode[STIX]{x1D6EC}$
being an arbitrary small category. We define the site
$\unicode[STIX]{x1D6EC}$
being an arbitrary small category. We define the site
![]() ${\mathcal{C}}/F$
fibered over
${\mathcal{C}}/F$
fibered over
![]() $F$
as follows: The objects are all pairs
$F$
as follows: The objects are all pairs
![]() $(X,\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
with
$(X,\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
with
![]() $X\in {\mathcal{C}}$
,
$X\in {\mathcal{C}}$
,
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $\unicode[STIX]{x1D6FC}\in F(\unicode[STIX]{x1D706})(X)$
. The morphisms from
$\unicode[STIX]{x1D6FC}\in F(\unicode[STIX]{x1D706})(X)$
. The morphisms from
![]() $(X,\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
to
$(X,\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
to
![]() $(Y,\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FD})$
are all commutative diagrams in the category of presheaves on
$(Y,\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FD})$
are all commutative diagrams in the category of presheaves on
![]() ${\mathcal{C}}$
${\mathcal{C}}$
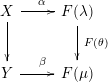
for some morphism
![]() $\unicode[STIX]{x1D703}$
in
$\unicode[STIX]{x1D703}$
in
![]() $\unicode[STIX]{x1D6EC}$
. The covering families of
$\unicode[STIX]{x1D6EC}$
. The covering families of
![]() $(X,\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
are
$(X,\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC})$
are
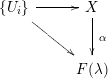
where
![]() $\{U_{i}\}\rightarrow X$
is a covering of
$\{U_{i}\}\rightarrow X$
is a covering of
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
In this section, we only use the case
![]() $\unicode[STIX]{x1D6EC}=\ast$
or
$\unicode[STIX]{x1D6EC}=\ast$
or
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6E5}^{\text{op}}$
. In the latter case, a functor
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6E5}^{\text{op}}$
. In the latter case, a functor
![]() $F\,:\,\unicode[STIX]{x1D6E5}^{\text{op}}\rightarrow \mathsf{PSh}({\mathcal{C}})$
is just a simplicial presheaf. In principle, we denote by
$F\,:\,\unicode[STIX]{x1D6E5}^{\text{op}}\rightarrow \mathsf{PSh}({\mathcal{C}})$
is just a simplicial presheaf. In principle, we denote by
![]() $F$
a simplicial presheaf.
$F$
a simplicial presheaf.
A.1 Sites fibered over presheaves
Let
![]() $X$
be a presheaf on
$X$
be a presheaf on
![]() ${\mathcal{C}}$
. The forgetful functor
${\mathcal{C}}$
. The forgetful functor
![]() $q\,:\,{\mathcal{C}}/X\rightarrow {\mathcal{C}}$
induces an adjunction
$q\,:\,{\mathcal{C}}/X\rightarrow {\mathcal{C}}$
induces an adjunction
Concretely, for
![]() $G\in s\mathsf{PSh}({\mathcal{C}}/X)$
and
$G\in s\mathsf{PSh}({\mathcal{C}}/X)$
and
![]() $U\in {\mathcal{C}}$
, the functor
$U\in {\mathcal{C}}$
, the functor
![]() $q^{\ast }$
is given by
$q^{\ast }$
is given by
Then, as in the proof of [Reference JardineJar15, Lemma 5.23], we see that
![]() $q^{\ast }$
preserves cofibrations and local weak equivalences. Therefore:
$q^{\ast }$
preserves cofibrations and local weak equivalences. Therefore:
Lemma A.2. The adjunction (A1) is a Quillen adjunction with respect to the local injective model structures.
A.2 Sites fibered over simplicial presheaves
Let
![]() $F$
be a simplicial presheaf on
$F$
be a simplicial presheaf on
![]() ${\mathcal{C}}$
. The canonical functor
${\mathcal{C}}$
. The canonical functor
![]() $j_{n}\,:\,{\mathcal{C}}/F_{n}\rightarrow {\mathcal{C}}/F$
induces an adjunction
$j_{n}\,:\,{\mathcal{C}}/F_{n}\rightarrow {\mathcal{C}}/F$
induces an adjunction
For
![]() $G\in s\mathsf{PSh}({\mathcal{C}}/F_{n})$
and
$G\in s\mathsf{PSh}({\mathcal{C}}/F_{n})$
and
![]() $(X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}F_{m})\in {\mathcal{C}}/F$
, we have
$(X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}F_{m})\in {\mathcal{C}}/F$
, we have
It follows that
![]() $j_{n}^{\ast }$
preserves cofibrations and local weak equivalences. Hence:
$j_{n}^{\ast }$
preserves cofibrations and local weak equivalences. Hence:
Lemma A.3. For every
![]() $n\geqslant 0$
, the adjunction (A2) is a Quillen adjunction with respect to the local injective model structures.
$n\geqslant 0$
, the adjunction (A2) is a Quillen adjunction with respect to the local injective model structures.
Remark A.4. The adjunctions (A1) and (A2) are also Quillen adjunctions with respect to the local projective model structures. Since projective fibrations are defined levelwise, it is clear that the forgetful functors
![]() $q_{\ast }$
and
$q_{\ast }$
and
![]() $j_{n\ast }$
preserve projective fibrations and trivial projective fibrations.
$j_{n\ast }$
preserve projective fibrations and trivial projective fibrations.
For simplicial presheaves
![]() $G,H$
on
$G,H$
on
![]() ${\mathcal{C}}$
, let
${\mathcal{C}}$
, let
![]() $\mathbf{hom}(G,H)$
be the function complex, that is, the simplicial set given by
$\mathbf{hom}(G,H)$
be the function complex, that is, the simplicial set given by
Let
![]() $j\,:\,{\mathcal{C}}/F\rightarrow {\mathcal{C}}$
be the forgetful functor, which induces
$j\,:\,{\mathcal{C}}/F\rightarrow {\mathcal{C}}$
be the forgetful functor, which induces
Here is the main result in this section, which is a generalization of [Reference JardineJar15, Proposition 5.29].
Theorem A.5. Let
![]() $Z$
be an injective fibrant object in
$Z$
be an injective fibrant object in
![]() $s\mathsf{PSh}({\mathcal{C}})$
and
$s\mathsf{PSh}({\mathcal{C}})$
and
![]() $W$
an injective fibrant replacement of
$W$
an injective fibrant replacement of
![]() $j_{\ast }Z$
in
$j_{\ast }Z$
in
![]() $s\mathsf{PSh}({\mathcal{C}}/F)$
. Then we have a weak equivalence
$s\mathsf{PSh}({\mathcal{C}}/F)$
. Then we have a weak equivalence
In particular, for any presheaf
![]() $A$
of complexes of abelian groups on
$A$
of complexes of abelian groups on
![]() ${\mathcal{C}}$
, we have an isomorphism
${\mathcal{C}}$
, we have an isomorphism
A.3 Preliminaries to the proof
A.3.1 Homotopy limits
Let
![]() $I$
be a small category. Recall that the homotopy limit of a functor
$I$
be a small category. Recall that the homotopy limit of a functor
![]() $X\,:\,I\rightarrow s\mathsf{Set}$
(
$X\,:\,I\rightarrow s\mathsf{Set}$
(
![]() $s\mathsf{Set}=$
the category of simplicial sets) is defined by
$s\mathsf{Set}=$
the category of simplicial sets) is defined by
where
![]() $I\downarrow -$
is the functor
$I\downarrow -$
is the functor
![]() $I\rightarrow \mathsf{Cat}$
assigning the comma category
$I\rightarrow \mathsf{Cat}$
assigning the comma category
![]() $I\downarrow i$
to each
$I\downarrow i$
to each
![]() $i\in I$
. Note that the final map
$i\in I$
. Note that the final map
![]() $B(I\downarrow -)\rightarrow \ast$
in
$B(I\downarrow -)\rightarrow \ast$
in
![]() $s\mathsf{Set}^{I}$
is a sectionwise weak equivalence. Hence, in case
$s\mathsf{Set}^{I}$
is a sectionwise weak equivalence. Hence, in case
![]() $X$
is an injective fibrant, we have a weak equivalence
$X$
is an injective fibrant, we have a weak equivalence
Lemma A.6. Let
![]() $Z$
be a sectionwise fibrant object in
$Z$
be a sectionwise fibrant object in
![]() $s\mathsf{PSh}({\mathcal{C}}/F)$
. Then there exists a natural weak equivalence
$s\mathsf{PSh}({\mathcal{C}}/F)$
. Then there exists a natural weak equivalence
Proof. We construct a morphism
in
![]() $s\mathsf{PSh}({\mathcal{C}}/F)$
, and show that it is a sectionwise weak equivalence between projective cofibrant objects in
$s\mathsf{PSh}({\mathcal{C}}/F)$
, and show that it is a sectionwise weak equivalence between projective cofibrant objects in
![]() $s\mathsf{PSh}({\mathcal{C}}/F)$
. Let
$s\mathsf{PSh}({\mathcal{C}}/F)$
. Let
![]() $X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}F_{n}$
be an object in
$X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}F_{n}$
be an object in
![]() ${\mathcal{C}}/F$
. Then we have
${\mathcal{C}}/F$
. Then we have
Hence, the sections at
![]() $(X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}F_{n})$
of the left hand side of (A4) are equal to the coequalizer of
$(X\xrightarrow[{}]{\unicode[STIX]{x1D6FC}}F_{n})$
of the left hand side of (A4) are equal to the coequalizer of
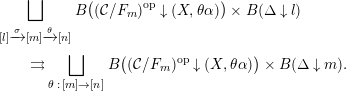 $$\begin{eqnarray}\displaystyle & & \displaystyle \bigsqcup _{[l]\xrightarrow[{}]{\unicode[STIX]{x1D70E}}[m]\xrightarrow[{}]{\unicode[STIX]{x1D703}}[n]}B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow (X,\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FC}))\times B(\unicode[STIX]{x1D6E5}\downarrow l)\nonumber\\ \displaystyle & & \displaystyle \qquad \rightrightarrows \bigsqcup _{\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]}B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow (X,\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FC}))\times B(\unicode[STIX]{x1D6E5}\downarrow m).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bigsqcup _{[l]\xrightarrow[{}]{\unicode[STIX]{x1D70E}}[m]\xrightarrow[{}]{\unicode[STIX]{x1D703}}[n]}B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow (X,\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FC}))\times B(\unicode[STIX]{x1D6E5}\downarrow l)\nonumber\\ \displaystyle & & \displaystyle \qquad \rightrightarrows \bigsqcup _{\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]}B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow (X,\unicode[STIX]{x1D703}\unicode[STIX]{x1D6FC}))\times B(\unicode[STIX]{x1D6E5}\downarrow m).\end{eqnarray}$$
For each
![]() $\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
, we define a functor
$\unicode[STIX]{x1D703}\,:\,[m]\rightarrow [n]$
, we define a functor
by sending
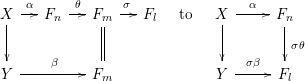
These functors induce a morphism of simplicial sets
which is functorial in
![]() $(X,\unicode[STIX]{x1D6FC})$
and kills the difference of (A5). Hence, it induces the desired morphism
$(X,\unicode[STIX]{x1D6FC})$
and kills the difference of (A5). Hence, it induces the desired morphism
![]() $\unicode[STIX]{x1D6F9}$
.
$\unicode[STIX]{x1D6F9}$
.
The coequalizer of (A5) is also equal to
where
![]() $\unicode[STIX]{x1D703}$
runs through
$\unicode[STIX]{x1D703}$
runs through
![]() $\unicode[STIX]{x1D6E5}\downarrow n$
, and it is contractible. It follows that the source and the target of
$\unicode[STIX]{x1D6E5}\downarrow n$
, and it is contractible. It follows that the source and the target of
![]() $\unicode[STIX]{x1D6F9}$
are sectionwise contractible, and thus
$\unicode[STIX]{x1D6F9}$
are sectionwise contractible, and thus
![]() $\unicode[STIX]{x1D6F9}$
is a sectionwise weak equivalence.
$\unicode[STIX]{x1D6F9}$
is a sectionwise weak equivalence.
According to [Reference HirschhornHir03, Corollary 14.8.8], diagrams of the form
![]() $B({\mathcal{E}}\downarrow -)$
are projective cofibrant. Since the adjunction (A2) is a Quillen adjunction with respect to the projective model structure (Remark A.4),
$B({\mathcal{E}}\downarrow -)$
are projective cofibrant. Since the adjunction (A2) is a Quillen adjunction with respect to the projective model structure (Remark A.4),
![]() $j_{m}^{\ast }B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -)$
is projective cofibrant. Hence, both sides of (A4) are projective cofibrant.
$j_{m}^{\ast }B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -)$
is projective cofibrant. Hence, both sides of (A4) are projective cofibrant.
It follows that
 $$\begin{eqnarray}\displaystyle \operatorname{holim}_{{\mathcal{C}}/F}j_{\ast }Z & = & \displaystyle \mathbf{hom}\Bigl(B(({\mathcal{C}}/F)^{\text{op}}\downarrow -),Z\Bigr)\nonumber\\ \displaystyle & \simeq & \displaystyle \mathbf{hom}\biggl(\operatorname{hocolim}_{m\in \unicode[STIX]{x1D6E5}^{\text{op}}}\Bigl(j_{m}^{\ast }B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -)\Bigr),Z\biggr)\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{holim}_{m\in \unicode[STIX]{x1D6E5}}\mathbf{hom}\Bigl(j_{m}^{\ast }B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -),Z\Bigr)\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{holim}_{m\in \unicode[STIX]{x1D6E5}}\mathbf{hom}\Bigl(B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -),j_{m\ast }Z\Bigr)\nonumber\\ \displaystyle & = & \displaystyle \operatorname{holim}_{m\in \unicode[STIX]{x1D6E5}}\operatorname{holim}_{{\mathcal{C}}/F_{m}}j_{m\ast }Z.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{holim}_{{\mathcal{C}}/F}j_{\ast }Z & = & \displaystyle \mathbf{hom}\Bigl(B(({\mathcal{C}}/F)^{\text{op}}\downarrow -),Z\Bigr)\nonumber\\ \displaystyle & \simeq & \displaystyle \mathbf{hom}\biggl(\operatorname{hocolim}_{m\in \unicode[STIX]{x1D6E5}^{\text{op}}}\Bigl(j_{m}^{\ast }B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -)\Bigr),Z\biggr)\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{holim}_{m\in \unicode[STIX]{x1D6E5}}\mathbf{hom}\Bigl(j_{m}^{\ast }B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -),Z\Bigr)\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{holim}_{m\in \unicode[STIX]{x1D6E5}}\mathbf{hom}\Bigl(B(({\mathcal{C}}/F_{m})^{\text{op}}\downarrow -),j_{m\ast }Z\Bigr)\nonumber\\ \displaystyle & = & \displaystyle \operatorname{holim}_{m\in \unicode[STIX]{x1D6E5}}\operatorname{holim}_{{\mathcal{C}}/F_{m}}j_{m\ast }Z.\nonumber\end{eqnarray}$$
The first isomorphism follows from [Reference HirschhornHir03, 18.4.5], the second one follows from [Reference HirschhornHir03, 18.1.10] and the third one is the adjunction (A2) of
![]() $j_{m}^{\ast }$
and
$j_{m}^{\ast }$
and
![]() $j_{m\ast }$
.
$j_{m\ast }$
.
A.3.2 Cosimplicial spaces
We call a cosimplicial object in
![]() $s\mathsf{Set}$
a cosimplicial space, and denote the category of cosimplicial spaces by
$s\mathsf{Set}$
a cosimplicial space, and denote the category of cosimplicial spaces by
![]() $cs\mathsf{Set}$
. Let
$cs\mathsf{Set}$
. Let
![]() $A$
be a cosimplicial space and
$A$
be a cosimplicial space and
![]() $S$
a simplicial presheaf on a site
$S$
a simplicial presheaf on a site
![]() ${\mathcal{C}}$
. We define a simplicial presheaf
${\mathcal{C}}$
. We define a simplicial presheaf
![]() $A\otimes S$
to be the coequalizer of
$A\otimes S$
to be the coequalizer of
Let
![]() $X$
be another simplicial presheaf on
$X$
be another simplicial presheaf on
![]() ${\mathcal{C}}$
. We define a cosimplicial space
${\mathcal{C}}$
. We define a cosimplicial space
![]() $\text{}\underline{\operatorname{Hom}}(S,X)$
by
$\text{}\underline{\operatorname{Hom}}(S,X)$
by
![]() $\text{}\underline{\operatorname{Hom}}(S,X)_{m}^{n}:=\operatorname{Hom}(S_{n},X_{m})$
.
$\text{}\underline{\operatorname{Hom}}(S,X)_{m}^{n}:=\operatorname{Hom}(S_{n},X_{m})$
.
Lemma A.7. There is a Quillen adjunction
with respect to the Bousfield–Kan model structure on
![]() $cs\mathsf{Set}$
[Reference Bousfield and KanBK72, X, Section 5] and the injective model structure on
$cs\mathsf{Set}$
[Reference Bousfield and KanBK72, X, Section 5] and the injective model structure on
![]() $s\mathsf{PSh}({\mathcal{C}})$
.
$s\mathsf{PSh}({\mathcal{C}})$
.
Proof. It is clear that (A6) is an adjunction. We show that
![]() $\text{}\underline{\operatorname{Hom}}(S,-)$
preserves fibrations and trivial fibrations.
$\text{}\underline{\operatorname{Hom}}(S,-)$
preserves fibrations and trivial fibrations.
Let
![]() $DS_{n}$
be the coequalizer of
$DS_{n}$
be the coequalizer of
which is a subpresheaf of
![]() $S_{n}$
. Then, for a simplicial presheaf
$S_{n}$
. Then, for a simplicial presheaf
![]() $X$
,
$X$
,
![]() $\mathbf{hom}(DS_{n},X)$
is the
$\mathbf{hom}(DS_{n},X)$
is the
![]() $(n-1)$
th matching space [Reference Bousfield and KanBK72, X, Section 4.5] of
$(n-1)$
th matching space [Reference Bousfield and KanBK72, X, Section 4.5] of
![]() $\text{}\underline{\operatorname{Hom}}(S,X)$
. Let
$\text{}\underline{\operatorname{Hom}}(S,X)$
. Let
![]() $X\rightarrow Y$
be an injective fibration (resp. injective trivial fibration) of simplicial presheaves. Since
$X\rightarrow Y$
be an injective fibration (resp. injective trivial fibration) of simplicial presheaves. Since
![]() $DS_{n}\rightarrow S_{n}$
is a cofibration, the induced map
$DS_{n}\rightarrow S_{n}$
is a cofibration, the induced map
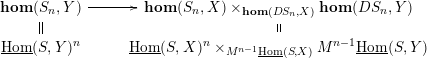
is a fibration (resp. trivial fibration). This proves the lemma.
A.4 Proof of Theorem A.5
Now, we are given an injective fibrant object
![]() $Z$
in
$Z$
in
![]() $s\mathsf{PSh}({\mathcal{C}})$
and an injective fibrant replacement
$s\mathsf{PSh}({\mathcal{C}})$
and an injective fibrant replacement
![]() $W$
of
$W$
of
![]() $j_{\ast }Z$
in
$j_{\ast }Z$
in
![]() $s\mathsf{PSh}({\mathcal{C}}/F)$
.
$s\mathsf{PSh}({\mathcal{C}}/F)$
.
First, we show that
![]() $j_{\ast }Z\rightarrow W$
is a sectionwise weak equivalence. By Lemma A.3,
$j_{\ast }Z\rightarrow W$
is a sectionwise weak equivalence. By Lemma A.3,
![]() $j_{n\ast }\,:\,s\mathsf{PSh}({\mathcal{C}}/F)\rightarrow s\mathsf{PSh}({\mathcal{C}}/F_{n})$
preserves injective fibrations. Put
$j_{n\ast }\,:\,s\mathsf{PSh}({\mathcal{C}}/F)\rightarrow s\mathsf{PSh}({\mathcal{C}}/F_{n})$
preserves injective fibrations. Put
![]() $q_{n}:=j\circ j_{n}\,:\,{\mathcal{C}}/F_{n}\rightarrow {\mathcal{C}}$
. By Lemma A.2,
$q_{n}:=j\circ j_{n}\,:\,{\mathcal{C}}/F_{n}\rightarrow {\mathcal{C}}$
. By Lemma A.2,
![]() $q_{n\ast }\,:\,s\mathsf{PSh}({\mathcal{C}})\rightarrow s\mathsf{PSh}({\mathcal{C}}/F_{n})$
also preserves injective fibrations. Hence,
$q_{n\ast }\,:\,s\mathsf{PSh}({\mathcal{C}})\rightarrow s\mathsf{PSh}({\mathcal{C}}/F_{n})$
also preserves injective fibrations. Hence,
![]() $q_{n\ast }Z\rightarrow j_{n\ast }W$
is a local weak equivalence between fibrant objects, and thus a sectionwise weak equivalence for every
$q_{n\ast }Z\rightarrow j_{n\ast }W$
is a local weak equivalence between fibrant objects, and thus a sectionwise weak equivalence for every
![]() $n$
.
$n$
.
We have seen that
![]() $j_{\ast }Z\rightarrow W$
is a sectionwise weak equivalence between sectionwise fibrant objects. Hence, by [Reference Bousfield and KanBK72, XI, 5.6], we have a weak equivalence
$j_{\ast }Z\rightarrow W$
is a sectionwise weak equivalence between sectionwise fibrant objects. Hence, by [Reference Bousfield and KanBK72, XI, 5.6], we have a weak equivalence
Since
![]() $W$
is an injective fibrant object on
$W$
is an injective fibrant object on
![]() ${\mathcal{C}}/F$
(locally, and thus for the indiscrete topology), it follows from (A3) that the right hand side of the above is weak equivalent to
${\mathcal{C}}/F$
(locally, and thus for the indiscrete topology), it follows from (A3) that the right hand side of the above is weak equivalent to
![]() $\mathbf{hom}(\ast ,W)$
. Hence, it remains to show that there is a weak equivalence
$\mathbf{hom}(\ast ,W)$
. Hence, it remains to show that there is a weak equivalence
Since
![]() $F$
is isomorphic to
$F$
is isomorphic to
![]() $\unicode[STIX]{x1D6E5}\otimes F$
, it follows from the adjunction (A6) that we have an isomorphism
$\unicode[STIX]{x1D6E5}\otimes F$
, it follows from the adjunction (A6) that we have an isomorphism
Now,
![]() $\text{}\underline{\operatorname{Hom}}(F,Z)$
is the cosimplicial space whose degree
$\text{}\underline{\operatorname{Hom}}(F,Z)$
is the cosimplicial space whose degree
![]() $n$
part is
$n$
part is
![]() $\lim _{X\in {\mathcal{C}}/F_{n}}Z(X)$
. Moreover, by Lemma A.7,
$\lim _{X\in {\mathcal{C}}/F_{n}}Z(X)$
. Moreover, by Lemma A.7,
![]() $\text{}\underline{\operatorname{Hom}}(F,Z)$
is a fibrant cosimplicial space. Therefore, by [Reference Bousfield and KanBK72, XI, 4.4],
$\text{}\underline{\operatorname{Hom}}(F,Z)$
is a fibrant cosimplicial space. Therefore, by [Reference Bousfield and KanBK72, XI, 4.4],
Since
![]() $q_{n\ast }Z$
is injective fibrant by Lemma A.2, it follows from (A3) that the canonical map
$q_{n\ast }Z$
is injective fibrant by Lemma A.2, it follows from (A3) that the canonical map
is a weak equivalence between fibrant objects. Therefore,
By Lemma A.6 and (A8, A9), we obtain the desired formula (A7).
Appendix B. Preliminaries on algebraic cycles
B.1 Moving lemma with modulus
Let
![]() $(X,D)\in \mathsf{MSm}$
. By a family of constructible subsets
$(X,D)\in \mathsf{MSm}$
. By a family of constructible subsets
![]() ${\mathcal{C}}=\{{C_{d}\}}_{d\in \mathbb{Z}}$
of
${\mathcal{C}}=\{{C_{d}\}}_{d\in \mathbb{Z}}$
of
![]() $X\setminus D$
we mean a nondecreasing family
$X\setminus D$
we mean a nondecreasing family
![]() $C_{d}\subset C_{d+1}$
such that
$C_{d}\subset C_{d+1}$
such that
![]() $\dim (C_{d})\leqslant d$
and
$\dim (C_{d})\leqslant d$
and
![]() $C_{\dim (X)}=X$
. Let
$C_{\dim (X)}=X$
. Let
![]() $z_{{\mathcal{C}}}^{i}(X|D,\bullet )\subset z^{i}(X|D,\bullet )$
be the subcomplex of cycles
$z_{{\mathcal{C}}}^{i}(X|D,\bullet )\subset z^{i}(X|D,\bullet )$
be the subcomplex of cycles
![]() $V\in z^{i}(X|D,n)$
such that for every
$V\in z^{i}(X|D,n)$
such that for every
![]() $d\in \mathbb{Z}$
and map of cubes
$d\in \mathbb{Z}$
and map of cubes
![]() $\Box ^{m}\rightarrow \Box ^{n}$
, the following inequality of dimensions holds:
$\Box ^{m}\rightarrow \Box ^{n}$
, the following inequality of dimensions holds:
![]() $\dim (|V|\times _{X\times \Box ^{n}}(C_{d}\times \Box ^{m}))\leqslant (d+m)-i.$
Of course, it suffices to consider face maps
$\dim (|V|\times _{X\times \Box ^{n}}(C_{d}\times \Box ^{m}))\leqslant (d+m)-i.$
Of course, it suffices to consider face maps
![]() $\Box ^{m}{\hookrightarrow}\Box ^{n}$
. When
$\Box ^{m}{\hookrightarrow}\Box ^{n}$
. When
![]() ${\mathcal{C}}$
is the trivial family
${\mathcal{C}}$
is the trivial family
![]() ${\mathcal{C}}_{\text{triv}}$
characterized by
${\mathcal{C}}_{\text{triv}}$
characterized by
![]() $C_{\dim (X)-1}=\emptyset$
, it is the same as
$C_{\dim (X)-1}=\emptyset$
, it is the same as
![]() $z^{i}(X|D,\bullet )$
. Given an equidimensional
$z^{i}(X|D,\bullet )$
. Given an equidimensional
![]() $k$
-scheme
$k$
-scheme
![]() $Y$
of finite type, we consider the presheaf
$Y$
of finite type, we consider the presheaf
![]() $z_{{\mathcal{C}}}^{i}(-\times Y|D\times Y,\bullet )$
on
$z_{{\mathcal{C}}}^{i}(-\times Y|D\times Y,\bullet )$
on
![]() $X_{\text{Nis}}$
defined by
$X_{\text{Nis}}$
defined by
The case
![]() $Y=\text{Spec}(k)$
is of primary importance, but we need the
$Y=\text{Spec}(k)$
is of primary importance, but we need the
![]() $Y=\mathbb{P}^{r-1}$
case as well when we consider projective bundles.
$Y=\mathbb{P}^{r-1}$
case as well when we consider projective bundles.
Theorem B.1. [Reference KaiKai15, Theorem 2]
In the notation as above, the inclusion
![]() $z_{{\mathcal{C}}}^{i}(-\times Y|D\times Y,\bullet ){\hookrightarrow}z^{i}(-\times Y|D\times Y,\bullet )$
is a quasi-isomorphism on
$z_{{\mathcal{C}}}^{i}(-\times Y|D\times Y,\bullet ){\hookrightarrow}z^{i}(-\times Y|D\times Y,\bullet )$
is a quasi-isomorphism on
![]() $X_{\text{Nis}}$
.
$X_{\text{Nis}}$
.
Cycle-theoretic operations often require proper intersection conditions for their well-definedness. If we can find a family
![]() ${\mathcal{C}}$
such that the operation is always defined on
${\mathcal{C}}$
such that the operation is always defined on
![]() $z_{{\mathcal{C}}}^{i}(-\times Y|D\times Y,\bullet )$
, Theorem B.1 allows us to conclude that the operation is well defined in the derived category
$z_{{\mathcal{C}}}^{i}(-\times Y|D\times Y,\bullet )$
, Theorem B.1 allows us to conclude that the operation is well defined in the derived category
![]() $D(X_{\text{Nis}})$
. For example, for a functor
$D(X_{\text{Nis}})$
. For example, for a functor
![]() $F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{MSm}$
as in Section 1.1 and an equidimensional
$F\,:\,\unicode[STIX]{x1D6EC}\rightarrow \mathsf{MSm}$
as in Section 1.1 and an equidimensional
![]() $k$
-scheme
$k$
-scheme
![]() $Y$
, the method in [Reference LevineLev98, page 94] (say) applied to the morphisms in
$Y$
, the method in [Reference LevineLev98, page 94] (say) applied to the morphisms in
![]() $\unicode[STIX]{x1D6EC}$
gives a canonical family
$\unicode[STIX]{x1D6EC}$
gives a canonical family
![]() ${\mathcal{C}}(\unicode[STIX]{x1D706})$
on
${\mathcal{C}}(\unicode[STIX]{x1D706})$
on
![]() $X_{\unicode[STIX]{x1D706}}$
such that the association
$X_{\unicode[STIX]{x1D706}}$
such that the association
is a presheaf on
![]() $\mathsf{MSm}^{\ast }$
. This and a similar argument give the presheaves
$\mathsf{MSm}^{\ast }$
. This and a similar argument give the presheaves
![]() $z_{\mathsf{rel}}^{i}$
and
$z_{\mathsf{rel}}^{i}$
and
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
in Section 1.1.
$p_{\ast }z_{\mathsf{rel}}^{i}$
in Section 1.1.
B.1.1 Further example: intersection product
Given a cycle
![]() $W\in z^{j}((X\setminus D)\times Y,n)$
, the cycles
$W\in z^{j}((X\setminus D)\times Y,n)$
, the cycles
![]() $V\in z^{i}(X|D,m)$
such that the intersection product
$V\in z^{i}(X|D,m)$
such that the intersection product
![]() $(V\times Y)\cdot W\in z^{i+j}(X\times Y|D\times Y,m+n)$
is well defined form a subcomplex of the form
$(V\times Y)\cdot W\in z^{i+j}(X\times Y|D\times Y,m+n)$
is well defined form a subcomplex of the form
![]() $z_{{\mathcal{C}}}^{i}(X|D,\bullet )$
. By Theorem B.1, it is isomorphic to
$z_{{\mathcal{C}}}^{i}(X|D,\bullet )$
. By Theorem B.1, it is isomorphic to
![]() $z^{i}(-|D,\bullet )$
in
$z^{i}(-|D,\bullet )$
in
![]() $D(X_{\text{Nis}})$
. If
$D(X_{\text{Nis}})$
. If
![]() $W$
vanishes by the differential in
$W$
vanishes by the differential in
![]() $z^{j}((X\setminus D)\times Y,\bullet )$
, we get a map of complexes
$z^{j}((X\setminus D)\times Y,\bullet )$
, we get a map of complexes
![]() $(-\times Y)\cdot W\,:\,z^{i}(-|D,\bullet )\rightarrow z^{i+j}(-\times Y|D\times Y,\bullet )$
in
$(-\times Y)\cdot W\,:\,z^{i}(-|D,\bullet )\rightarrow z^{i+j}(-\times Y|D\times Y,\bullet )$
in
![]() $D(X_{\text{Nis}})$
.
$D(X_{\text{Nis}})$
.
Or, letting
![]() $W$
vary in
$W$
vary in
![]() $z^{j}((-\setminus D)\times Y,\bullet )$
, we get a subcomplex
$z^{j}((-\setminus D)\times Y,\bullet )$
, we get a subcomplex
![]() $z^{i}(-|D,\bullet )\overset{\text{:D}}{\otimes }z^{j}((-\setminus D)\times Y,\bullet )$
of the usual tensor
$z^{i}(-|D,\bullet )\overset{\text{:D}}{\otimes }z^{j}((-\setminus D)\times Y,\bullet )$
of the usual tensor
![]() $\otimes$
where the intersection product is well defined. By the fact that a columnwise quasi-isomorphism of bicomplexes (suitably bounded) induces a quasi-isomorphism on the total complexes, we get a diagram in
$\otimes$
where the intersection product is well defined. By the fact that a columnwise quasi-isomorphism of bicomplexes (suitably bounded) induces a quasi-isomorphism on the total complexes, we get a diagram in
![]() $D(X_{\text{Nis}})$
:
$D(X_{\text{Nis}})$
:
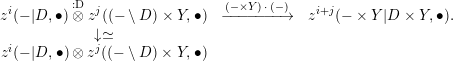 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}z^{i}(-|D,\bullet )\overset{\text{:D}}{\otimes }z^{j}((-\setminus D)\times Y,\bullet ) & \xrightarrow[{}]{(-\times Y)\,\cdot \,(-)} & z^{i+j}(-\times Y|D\times Y,\bullet ).\\ \downarrow \simeq & \\ z^{i}(-|D,\bullet )\otimes z^{j}((-\setminus D)\times Y,\bullet ) & \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}z^{i}(-|D,\bullet )\overset{\text{:D}}{\otimes }z^{j}((-\setminus D)\times Y,\bullet ) & \xrightarrow[{}]{(-\times Y)\,\cdot \,(-)} & z^{i+j}(-\times Y|D\times Y,\bullet ).\\ \downarrow \simeq & \\ z^{i}(-|D,\bullet )\otimes z^{j}((-\setminus D)\times Y,\bullet ) & \end{array}\end{eqnarray}$$
This is used when we construct maps
![]() $p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}$
in Section 1.3. Also, since
$p^{\ast }(-)\,\cdot \,\unicode[STIX]{x1D709}^{j}$
in Section 1.3. Also, since
![]() $z^{j}(X|D,\bullet )\subset z^{j}(X\setminus D,\bullet )$
, we get intersection product
$z^{j}(X|D,\bullet )\subset z^{j}(X\setminus D,\bullet )$
, we get intersection product
![]() $z_{\mathsf{rel}}^{i}\otimes z_{\mathsf{rel}}^{j}\rightarrow z_{\mathsf{rel}}^{i+j}$
in
$z_{\mathsf{rel}}^{i}\otimes z_{\mathsf{rel}}^{j}\rightarrow z_{\mathsf{rel}}^{i+j}$
in
![]() $D(\mathsf{MSm}^{\ast })$
.
$D(\mathsf{MSm}^{\ast })$
.
B.1.2 Yet another example: algebraic join
In the situation of Section 3.1, for each
![]() $W\in z^{j}(\mathbb{P}_{X\setminus D}^{s-1},n)$
, the cycles
$W\in z^{j}(\mathbb{P}_{X\setminus D}^{s-1},n)$
, the cycles
![]() $V\in z^{i}(\mathbb{P}_{X}^{r-1}|\mathbb{P}_{D}^{r-1},m)$
such that the join
$V\in z^{i}(\mathbb{P}_{X}^{r-1}|\mathbb{P}_{D}^{r-1},m)$
such that the join
![]() $V\#W\in z^{i+j}(\mathbb{P}_{X}^{r+s-1}|\mathbb{P}_{D}^{r+s-1},m+n)$
is well defined form a subcomplex of the form
$V\#W\in z^{i+j}(\mathbb{P}_{X}^{r+s-1}|\mathbb{P}_{D}^{r+s-1},m+n)$
is well defined form a subcomplex of the form
![]() $z_{{\mathcal{C}}}^{i}(\mathbb{P}_{X}^{r-1}|\mathbb{P}_{D}^{r-1},\bullet )$
for some
$z_{{\mathcal{C}}}^{i}(\mathbb{P}_{X}^{r-1}|\mathbb{P}_{D}^{r-1},\bullet )$
for some
![]() ${\mathcal{C}}$
on
${\mathcal{C}}$
on
![]() $X$
. One can find such a
$X$
. One can find such a
![]() ${\mathcal{C}}$
by applying [Reference LevineLev98, page 94] to the fiber dimensions of the projections
${\mathcal{C}}$
by applying [Reference LevineLev98, page 94] to the fiber dimensions of the projections
![]() $W_{|F}\rightarrow X$
with
$W_{|F}\rightarrow X$
with
![]() $F\subset \Box ^{n}$
being faces. By varying
$F\subset \Box ^{n}$
being faces. By varying
![]() $W$
as in the previous paragraph, we get a map
$W$
as in the previous paragraph, we get a map
![]() $\#\,:\,z^{i}(\mathbb{P}_{(-)}^{r-1}|\mathbb{P}_{D}^{r-1},\bullet )\overset{\text{:D}}{\otimes }z^{j}(\mathbb{P}_{(-\setminus D)}^{s-1},\bullet )\rightarrow z^{i}(\mathbb{P}_{(-)}^{r+s-1}|\mathbb{P}_{D}^{r+s-1},\bullet )$
in
$\#\,:\,z^{i}(\mathbb{P}_{(-)}^{r-1}|\mathbb{P}_{D}^{r-1},\bullet )\overset{\text{:D}}{\otimes }z^{j}(\mathbb{P}_{(-\setminus D)}^{s-1},\bullet )\rightarrow z^{i}(\mathbb{P}_{(-)}^{r+s-1}|\mathbb{P}_{D}^{r+s-1},\bullet )$
in
![]() $D(X_{\text{Nis}})$
. Carrying out this argument on
$D(X_{\text{Nis}})$
. Carrying out this argument on
![]() $\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{r}^{\mathsf{rel}}$
(or more generally on
$\mathsf{MSm}^{\ast }/\boldsymbol{X}_{r}^{\mathsf{rel}}\times \boldsymbol{X}_{r}^{\mathsf{rel}}$
(or more generally on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}\times B\text{GL}_{s}$
), we get the following diagram:
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}\times B\text{GL}_{s}$
), we get the following diagram:
which gives the algebraic join in
![]() $D(\mathsf{MSm}^{\ast }/B\text{GL}_{r}\times B\text{GL}_{s})$
.
$D(\mathsf{MSm}^{\ast }/B\text{GL}_{r}\times B\text{GL}_{s})$
.
B.2 Computing cup product
Here we give a formula which gives us explicit representatives for the cup product. This is used in Sections 1 and 2, where algebraic cycles are involved. In Section B.3, we prove results saying that the proper intersection of the lowest-degree representatives (in some sense) implies the proper intersection of all representatives, whereby we get well-defined intersection products of cohomology classes.
Consider a site
![]() ${\mathcal{C}}$
. Let us agree that the cup product of two cohomology classes
${\mathcal{C}}$
. Let us agree that the cup product of two cohomology classes
![]() $\unicode[STIX]{x1D719}\in H^{i}({\mathcal{C}},F)$
and
$\unicode[STIX]{x1D719}\in H^{i}({\mathcal{C}},F)$
and
![]() $\unicode[STIX]{x1D713}\in H^{j}({\mathcal{C}},G)$
(where
$\unicode[STIX]{x1D713}\in H^{j}({\mathcal{C}},G)$
(where
![]() $F,G$
are objects in the derived category of complexes of abelian sheaves) is defined as the derived tensor of the two maps
$F,G$
are objects in the derived category of complexes of abelian sheaves) is defined as the derived tensor of the two maps
![]() $\mathbb{Z}\rightarrow F[i]$
,
$\mathbb{Z}\rightarrow F[i]$
,
![]() $\mathbb{Z}\rightarrow G[j]$
representing them:
$\mathbb{Z}\rightarrow G[j]$
representing them:
If we are given a map into another object
![]() $F\otimes ^{L}G\rightarrow E$
, then we get its image in
$F\otimes ^{L}G\rightarrow E$
, then we get its image in
![]() $H^{i+j}({\mathcal{C}},E)$
which is often denoted by
$H^{i+j}({\mathcal{C}},E)$
which is often denoted by
![]() $\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713}$
again.
$\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713}$
again.
If we are given a quasi-isomorphism
![]() $\unicode[STIX]{x1D700}\,:\,{\mathcal{Z}}\rightarrow \mathbb{Z}$
and a morphism
$\unicode[STIX]{x1D700}\,:\,{\mathcal{Z}}\rightarrow \mathbb{Z}$
and a morphism
![]() $D\,:\,{\mathcal{Z}}\rightarrow {\mathcal{Z}}\otimes ^{L}{\mathcal{Z}}$
such that
$D\,:\,{\mathcal{Z}}\rightarrow {\mathcal{Z}}\otimes ^{L}{\mathcal{Z}}$
such that
![]() $(\unicode[STIX]{x1D700}\otimes ^{L}\unicode[STIX]{x1D700})\circ D=\unicode[STIX]{x1D700}$
as maps
$(\unicode[STIX]{x1D700}\otimes ^{L}\unicode[STIX]{x1D700})\circ D=\unicode[STIX]{x1D700}$
as maps
![]() ${\mathcal{Z}}\rightrightarrows \mathbb{Z}\otimes ^{L}\mathbb{Z}=\mathbb{Z}$
, then the cup product of classes represented by maps
${\mathcal{Z}}\rightrightarrows \mathbb{Z}\otimes ^{L}\mathbb{Z}=\mathbb{Z}$
, then the cup product of classes represented by maps
![]() $\unicode[STIX]{x1D719}\,:\,{\mathcal{Z}}\rightarrow F[i]$
and
$\unicode[STIX]{x1D719}\,:\,{\mathcal{Z}}\rightarrow F[i]$
and
![]() $\unicode[STIX]{x1D713}\,:\,{\mathcal{Z}}\rightarrow G[j]$
can be computed as the composition
$\unicode[STIX]{x1D713}\,:\,{\mathcal{Z}}\rightarrow G[j]$
can be computed as the composition
![]() ${\mathcal{Z}}\xrightarrow[{}]{D}{\mathcal{Z}}\otimes ^{L}{\mathcal{Z}}\xrightarrow[{}]{\unicode[STIX]{x1D719}\otimes ^{L}\unicode[STIX]{x1D713}}F\otimes ^{L}G[i+j].$
${\mathcal{Z}}\xrightarrow[{}]{D}{\mathcal{Z}}\otimes ^{L}{\mathcal{Z}}\xrightarrow[{}]{\unicode[STIX]{x1D719}\otimes ^{L}\unicode[STIX]{x1D713}}F\otimes ^{L}G[i+j].$
B.2.1 The case of a site fibered over a simplicial presheaf
Let
![]() $\boldsymbol{X}$
be a simplicial presheaf on
$\boldsymbol{X}$
be a simplicial presheaf on
![]() ${\mathcal{C}}$
. We are interested in the site
${\mathcal{C}}$
. We are interested in the site
![]() ${\mathcal{C}}/\boldsymbol{X}$
. Denote by
${\mathcal{C}}/\boldsymbol{X}$
. Denote by
![]() $\unicode[STIX]{x1D6E5}$
the simplicial presheaf defined by
$\unicode[STIX]{x1D6E5}$
the simplicial presheaf defined by
![]() $(X,n,\unicode[STIX]{x1D6FC})\mapsto \unicode[STIX]{x1D6E5}^{n}$
. The projection
$(X,n,\unicode[STIX]{x1D6FC})\mapsto \unicode[STIX]{x1D6E5}^{n}$
. The projection
![]() $\unicode[STIX]{x1D6E5}\rightarrow \text{pt}$
induces a quasi-isomorphism
$\unicode[STIX]{x1D6E5}\rightarrow \text{pt}$
induces a quasi-isomorphism
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\rightarrow \mathbb{Z}$
.
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\rightarrow \mathbb{Z}$
.
For integers
![]() $0\leqslant k\leqslant l\leqslant n$
, we denote by
$0\leqslant k\leqslant l\leqslant n$
, we denote by
![]() $[k,l]\subset [n]$
the subset
$[k,l]\subset [n]$
the subset
![]() $\{k,k+1\ldots ,l\}$
. By abuse of notation, let the same symbol also denote the inclusion map
$\{k,k+1\ldots ,l\}$
. By abuse of notation, let the same symbol also denote the inclusion map
![]() $[l-k]{\hookrightarrow}[n]$
onto it. The complex
$[l-k]{\hookrightarrow}[n]$
onto it. The complex
![]() $\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}$
has the coalgebra structure (the Alexander–Whitney map)
$\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}$
has the coalgebra structure (the Alexander–Whitney map)
![]() $D\,:\,\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\rightarrow (\mathbb{Z}\otimes \unicode[STIX]{x1D6E5})\otimes (\mathbb{Z}\otimes \unicode[STIX]{x1D6E5})$
by which
$D\,:\,\mathbb{Z}\otimes \unicode[STIX]{x1D6E5}\rightarrow (\mathbb{Z}\otimes \unicode[STIX]{x1D6E5})\otimes (\mathbb{Z}\otimes \unicode[STIX]{x1D6E5})$
by which
![]() $\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
is mapped to the sum:
$\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}$
is mapped to the sum:
Now suppose that
![]() ${\mathcal{C}}$
is a category of schemes equipped with the Zariski topology (or finer), and that
${\mathcal{C}}$
is a category of schemes equipped with the Zariski topology (or finer), and that
![]() $\unicode[STIX]{x1D6E5}$
is covered by two open simplicial subpresheaves
$\unicode[STIX]{x1D6E5}$
is covered by two open simplicial subpresheaves
![]() $\unicode[STIX]{x1D6E5}^{\circ }$
and
$\unicode[STIX]{x1D6E5}^{\circ }$
and
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
. Set
$\unicode[STIX]{x1D6E5}^{\ast }$
. Set
![]() $\unicode[STIX]{x1D6E5}\text{}^{\circ \ast }:=\unicode[STIX]{x1D6E5}^{\circ }\cap \unicode[STIX]{x1D6E5}^{\ast }$
. In this case we have a weak equivalence
$\unicode[STIX]{x1D6E5}\text{}^{\circ \ast }:=\unicode[STIX]{x1D6E5}^{\circ }\cap \unicode[STIX]{x1D6E5}^{\ast }$
. In this case we have a weak equivalence
The complex
![]() ${\mathcal{Z}}$
has a coalgebra structure
${\mathcal{Z}}$
has a coalgebra structure
![]() $D\,:\,{\mathcal{Z}}\rightarrow {\mathcal{Z}}\otimes {\mathcal{Z}}$
. Writing it down is equivalent to writing down the formula for the cup product, so we do the latter. Let
$D\,:\,{\mathcal{Z}}\rightarrow {\mathcal{Z}}\otimes {\mathcal{Z}}$
. Writing it down is equivalent to writing down the formula for the cup product, so we do the latter. Let
![]() $\unicode[STIX]{x1D719}\,:\,{\mathcal{Z}}\rightarrow F$
and
$\unicode[STIX]{x1D719}\,:\,{\mathcal{Z}}\rightarrow F$
and
![]() $\unicode[STIX]{x1D713}\,:\,{\mathcal{Z}}\rightarrow G$
be maps of complexes. For each object
$\unicode[STIX]{x1D713}\,:\,{\mathcal{Z}}\rightarrow G$
be maps of complexes. For each object
![]() $(X,n,\unicode[STIX]{x1D6FC})\in {\mathcal{C}}/\boldsymbol{X}$
and degree
$(X,n,\unicode[STIX]{x1D6FC})\in {\mathcal{C}}/\boldsymbol{X}$
and degree
![]() $m$
, the map
$m$
, the map
![]() $\unicode[STIX]{x1D719}$
gives the data:
$\unicode[STIX]{x1D719}$
gives the data:
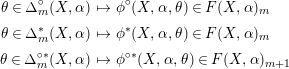 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{\circ }(X,\unicode[STIX]{x1D6FC}) & \mapsto & \displaystyle \unicode[STIX]{x1D719}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})\in F(X,\unicode[STIX]{x1D6FC})_{m}\nonumber\\ \displaystyle \unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{\ast }(X,\unicode[STIX]{x1D6FC}) & \mapsto & \displaystyle \unicode[STIX]{x1D719}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})\in F(X,\unicode[STIX]{x1D6FC})_{m}\nonumber\\ \displaystyle \unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}\text{}_{m}^{\circ \ast }(X,\unicode[STIX]{x1D6FC}) & \mapsto & \displaystyle \unicode[STIX]{x1D719}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})\in F(X,\unicode[STIX]{x1D6FC})_{m+1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{\circ }(X,\unicode[STIX]{x1D6FC}) & \mapsto & \displaystyle \unicode[STIX]{x1D719}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})\in F(X,\unicode[STIX]{x1D6FC})_{m}\nonumber\\ \displaystyle \unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{\ast }(X,\unicode[STIX]{x1D6FC}) & \mapsto & \displaystyle \unicode[STIX]{x1D719}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})\in F(X,\unicode[STIX]{x1D6FC})_{m}\nonumber\\ \displaystyle \unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}\text{}_{m}^{\circ \ast }(X,\unicode[STIX]{x1D6FC}) & \mapsto & \displaystyle \unicode[STIX]{x1D719}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})\in F(X,\unicode[STIX]{x1D6FC})_{m+1}\nonumber\end{eqnarray}$$
(and similarly
![]() $\unicode[STIX]{x1D713}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
,
$\unicode[STIX]{x1D713}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
,
![]() $\unicode[STIX]{x1D713}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
and
$\unicode[STIX]{x1D713}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
and
![]() $\unicode[STIX]{x1D713}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
). Then their cup product in
$\unicode[STIX]{x1D713}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$
). Then their cup product in
![]() $H^{0}({\mathcal{C}},F\otimes G)$
is represented by the data:
$H^{0}({\mathcal{C}},F\otimes G)$
is represented by the data:
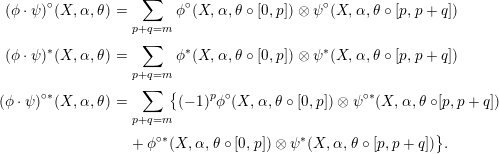 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713})^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}) & = & \displaystyle \mathop{\sum }_{p+q=m}\unicode[STIX]{x1D719}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [p,p+q])\nonumber\\ \displaystyle (\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713})^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}) & = & \displaystyle \mathop{\sum }_{p+q=m}\unicode[STIX]{x1D719}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [p,p+q])\nonumber\\ \displaystyle (\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713})\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}) & = & \displaystyle \mathop{\sum }_{p+q=m}\!\!\big\{(-1)^{p}\unicode[STIX]{x1D719}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ \![p,p+q])\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [p,p+q])\big\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713})^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}) & = & \displaystyle \mathop{\sum }_{p+q=m}\unicode[STIX]{x1D719}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [p,p+q])\nonumber\\ \displaystyle (\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713})^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}) & = & \displaystyle \mathop{\sum }_{p+q=m}\unicode[STIX]{x1D719}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [p,p+q])\nonumber\\ \displaystyle (\unicode[STIX]{x1D719}\,\cdot \,\unicode[STIX]{x1D713})\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}) & = & \displaystyle \mathop{\sum }_{p+q=m}\!\!\big\{(-1)^{p}\unicode[STIX]{x1D719}^{\circ }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ \![p,p+q])\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D719}\text{}^{\circ \ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [0,p])\otimes \unicode[STIX]{x1D713}^{\ast }(X,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\circ [p,p+q])\big\}.\nonumber\end{eqnarray}$$
B.3 Proper intersection lemmas
The statement of the next lemma may appear to be a little involved, but its proof is easy. (The interested reader can try the
![]() $n=0$
case first.) Below, we deduce some of its consequences which are useful in checking the well-definedness of cup products.
$n=0$
case first.) Below, we deduce some of its consequences which are useful in checking the well-definedness of cup products.
Lemma B.2. Let
![]() $X$
be an algebraic scheme and
$X$
be an algebraic scheme and
![]() $V$
a closed subscheme of
$V$
a closed subscheme of
![]() $X\times \Box ^{n}$
. Let
$X\times \Box ^{n}$
. Let
![]() $G,H$
be functions on
$G,H$
be functions on
![]() $X\times \Box ^{n}$
which and whose restrictions to
$X\times \Box ^{n}$
which and whose restrictions to
![]() $V$
are nowhere zero divisors. Assume further that
$V$
are nowhere zero divisors. Assume further that
![]() $V$
,
$V$
,
![]() $\text{div}(G)$
,
$\text{div}(G)$
,
![]() $\text{div}(H)$
,
$\text{div}(H)$
,
![]() $V\cap \text{div}(G)$
and
$V\cap \text{div}(G)$
and
![]() $V\cap \text{div}(H)$
satisfy the face condition in
$V\cap \text{div}(H)$
satisfy the face condition in
![]() $X\times \Box ^{n}$
. Then the function
$X\times \Box ^{n}$
. Then the function
![]() $H+t_{n+1}(G-H)$
on
$H+t_{n+1}(G-H)$
on
![]() $X\times \Box ^{n+1}$
and its restriction to
$X\times \Box ^{n+1}$
and its restriction to
![]() $V\times \Box ^{1}$
are nowhere zero divisors, and the intersection
$V\times \Box ^{1}$
are nowhere zero divisors, and the intersection
![]() $(V\times \Box ^{1})\cap \text{div}(H+t_{n+1}(G-H))$
satisfies the face condition.
$(V\times \Box ^{1})\cap \text{div}(H+t_{n+1}(G-H))$
satisfies the face condition.
B.3.1 Semi-simplicial schemes
In Sections 1 and 2 we are interested in the following situation. Let
![]() $X_{\bullet }$
be a semi-simplicial scheme with flat face maps and
$X_{\bullet }$
be a semi-simplicial scheme with flat face maps and
![]() $i\geqslant 1$
an integer. Let
$i\geqslant 1$
an integer. Let
![]() $L\text{}^{(a)}$
be a line bundle on
$L\text{}^{(a)}$
be a line bundle on
![]() $X_{\bullet }$
given for each
$X_{\bullet }$
given for each
![]() $a\in \{1,\ldots ,i\}$
equipped with a section
$a\in \{1,\ldots ,i\}$
equipped with a section
![]() $\unicode[STIX]{x1D70E}\text{}^{(a)}\in \unicode[STIX]{x1D6E4}(X_{0},L\text{}_{0}^{(a)})$
which is everywhere a nonzero divisor. Section 1.2 gives meromorphic functions
$\unicode[STIX]{x1D70E}\text{}^{(a)}\in \unicode[STIX]{x1D6E4}(X_{0},L\text{}_{0}^{(a)})$
which is everywhere a nonzero divisor. Section 1.2 gives meromorphic functions
![]() $F\text{}_{n}^{(a)}:=F\text{}_{n}^{(\unicode[STIX]{x1D70E}\text{}^{(a)})}$
on
$F\text{}_{n}^{(a)}:=F\text{}_{n}^{(\unicode[STIX]{x1D70E}\text{}^{(a)})}$
on
![]() $X_{n}\times \Box ^{n}$
and cycles
$X_{n}\times \Box ^{n}$
and cycles
Given a subset
![]() $S\subset [n]$
with
$S\subset [n]$
with
![]() $s+1$
elements, we denote again by
$s+1$
elements, we denote again by
![]() $S$
the inclusion
$S$
the inclusion
![]() $[s]{\hookrightarrow}[n]$
onto
$[s]{\hookrightarrow}[n]$
onto
![]() $S$
. Write
$S$
. Write
![]() $F\text{}^{(a)}(S)$
and
$F\text{}^{(a)}(S)$
and
![]() $\unicode[STIX]{x1D6E4}\text{}^{(a)}(S)$
for the pull-backs of
$\unicode[STIX]{x1D6E4}\text{}^{(a)}(S)$
for the pull-backs of
![]() $F\text{}_{s}^{(a)}$
and
$F\text{}_{s}^{(a)}$
and
![]() $\unicode[STIX]{x1D6E4}\text{}_{s}^{(a)}$
by the map
$\unicode[STIX]{x1D6E4}\text{}_{s}^{(a)}$
by the map
![]() $X(S)\times \text{id}_{\Box ^{s}}$
:
$X(S)\times \text{id}_{\Box ^{s}}$
:
![]() $X_{n}\times \Box ^{s}\rightarrow X_{s}\times \Box ^{s}$
. If we denote by
$X_{n}\times \Box ^{s}\rightarrow X_{s}\times \Box ^{s}$
. If we denote by
![]() $d_{k}\,:\,[s-1]{\hookrightarrow}[s]$
the face maps (
$d_{k}\,:\,[s-1]{\hookrightarrow}[s]$
the face maps (
![]() $0\leqslant k\leqslant s$
), the functions
$0\leqslant k\leqslant s$
), the functions
![]() $F\text{}^{(a)}(S)$
admit an inductive definition (on the size of
$F\text{}^{(a)}(S)$
admit an inductive definition (on the size of
![]() $S$
):
$S$
):
Lemma 1.10 in the main body of the article is a consequence of the following.
Lemma B.3. Keep the notation above and let
![]() $m\geqslant 0$
be an integer. Suppose that the Cartier divisors
$m\geqslant 0$
be an integer. Suppose that the Cartier divisors
![]() $\unicode[STIX]{x1D6E4}\text{}^{(a)}(v_{k_{a}}^{[m]})$
(
$\unicode[STIX]{x1D6E4}\text{}^{(a)}(v_{k_{a}}^{[m]})$
(
![]() $a=1,\ldots ,i$
) on
$a=1,\ldots ,i$
) on
![]() $X_{m}$
form a local complete intersection for every choice of indices
$X_{m}$
form a local complete intersection for every choice of indices
![]() $0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant m$
. Then for every choice of nonempty subsets
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant m$
. Then for every choice of nonempty subsets
![]() $S_{1}\leqslant \ldots \leqslant S_{i}$
of
$S_{1}\leqslant \ldots \leqslant S_{i}$
of
![]() $[m]$
, the Cartier divisors on
$[m]$
, the Cartier divisors on
![]() $X_{m}\times \Box ^{m}$
:
$X_{m}\times \Box ^{m}$
:
form a complete intersection, and the intersection satisfies the face condition. Consequently, their intersection product belongs to
![]() $z^{i}(X_{m},m)$
.
$z^{i}(X_{m},m)$
.
B.3.2 Variant
In Section 2, we are interested in a little more involved situation where each
![]() $X_{n}$
admits an open cover
$X_{n}$
admits an open cover
![]() $X_{n}=X_{n}^{\circ }\cup X_{n}^{\ast }$
and the collections of schemes
$X_{n}=X_{n}^{\circ }\cup X_{n}^{\ast }$
and the collections of schemes
![]() $(X_{n}^{\circ })_{n}$
,
$(X_{n}^{\circ })_{n}$
,
![]() $(X_{n}^{\ast })_{n}$
form semi-simplicial subschemes. Write
$(X_{n}^{\ast })_{n}$
form semi-simplicial subschemes. Write
![]() $X\text{}_{n}^{\circ \ast }:=X_{n}^{\circ }\cap X_{n}^{\ast }$
. Suppose that we are given sections
$X\text{}_{n}^{\circ \ast }:=X_{n}^{\circ }\cap X_{n}^{\ast }$
. Suppose that we are given sections
![]() $\unicode[STIX]{x1D70E}\text{}^{(a)\circ }\in \unicode[STIX]{x1D6E4}(X_{0}^{\circ },L_{0})$
and
$\unicode[STIX]{x1D70E}\text{}^{(a)\circ }\in \unicode[STIX]{x1D6E4}(X_{0}^{\circ },L_{0})$
and
![]() $\unicode[STIX]{x1D70E}\text{}^{(a)\ast }\in \unicode[STIX]{x1D6E4}(X_{0}^{\ast },L_{0})$
(
$\unicode[STIX]{x1D70E}\text{}^{(a)\ast }\in \unicode[STIX]{x1D6E4}(X_{0}^{\ast },L_{0})$
(
![]() $1\leqslant a\leqslant i$
) which are everywhere nonzero divisors. Invariants associated with
$1\leqslant a\leqslant i$
) which are everywhere nonzero divisors. Invariants associated with
![]() $\unicode[STIX]{x1D70E}\text{}^{(a)\circ }$
are indicated by superscripts
$\unicode[STIX]{x1D70E}\text{}^{(a)\circ }$
are indicated by superscripts
![]() $(-)\text{}^{(a)\circ }$
, and
$(-)\text{}^{(a)\circ }$
, and
![]() $\unicode[STIX]{x1D70E}\text{}^{(a)\ast }$
by
$\unicode[STIX]{x1D70E}\text{}^{(a)\ast }$
by
![]() $(-)\text{}^{(a)\ast }$
.
$(-)\text{}^{(a)\ast }$
.
The homotopy in equation (1) gives
For a subset
![]() $S\subset [m]$
with
$S\subset [m]$
with
![]() $s+1$
elements, let
$s+1$
elements, let
![]() $F\text{}^{(a)\circ \ast }(S)$
be the pull-back of
$F\text{}^{(a)\circ \ast }(S)$
be the pull-back of
![]() $F\text{}_{s}^{(a)\circ \ast }$
by the map
$F\text{}_{s}^{(a)\circ \ast }$
by the map
![]() $X(S)\times \text{id}_{\Box ^{s+1}}$
:
$X(S)\times \text{id}_{\Box ^{s+1}}$
:
![]() $X_{m}\times \Box ^{s+1}\rightarrow X_{s}\times \Box ^{s+1}$
.
$X_{m}\times \Box ^{s+1}\rightarrow X_{s}\times \Box ^{s+1}$
.
The proof of the following lemma is similar to the previous one. One applies it to the simplicial schemes
![]() $X\times \unicode[STIX]{x1D6E5}^{n}$
with open covering in degree
$X\times \unicode[STIX]{x1D6E5}^{n}$
with open covering in degree
![]() $m$
:
$m$
:
![]() $X\times \unicode[STIX]{x1D6E5}_{m}^{n}=\bigsqcup _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}}((X\setminus D)\cup (X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }))$
to verify the well-definedness of the cup product in formula (5), Section 2.2.
$X\times \unicode[STIX]{x1D6E5}_{m}^{n}=\bigsqcup _{\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6E5}_{m}^{n}}((X\setminus D)\cup (X_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}^{\ast }))$
to verify the well-definedness of the cup product in formula (5), Section 2.2.
In the lemma, for a subset
![]() $S\subset [n]$
we denote by
$S\subset [n]$
we denote by
![]() $\text{pr}_{S}$
the projection
$\text{pr}_{S}$
the projection
![]() $\Box ^{n}\rightarrow \Box ^{s}$
to the
$\Box ^{n}\rightarrow \Box ^{s}$
to the
![]() $S(1),\ldots ,S(s)$
th components. For nonempty subsets
$S(1),\ldots ,S(s)$
th components. For nonempty subsets
![]() $S$
,
$S$
,
![]() $T$
of
$T$
of
![]() $[n]$
, we write
$[n]$
, we write
![]() $S\leqslant T$
to mean the relation: (the maximum element of
$S\leqslant T$
to mean the relation: (the maximum element of
![]() $S$
)
$S$
)
![]() ${\leqslant}$
(the minimum element of
${\leqslant}$
(the minimum element of
![]() $T$
). Denote by
$T$
). Denote by
![]() $S+1$
the subset
$S+1$
the subset
![]() $\{k+1~|~k\in S\}$
of
$\{k+1~|~k\in S\}$
of
![]() $[n+1]$
.
$[n+1]$
.
Lemma B.4. Keep the notation above and let
![]() $b\in \{1,\ldots ,i\}$
. Assume that the Cartier divisors
$b\in \{1,\ldots ,i\}$
. Assume that the Cartier divisors
![]() $\unicode[STIX]{x1D6E4}\text{}^{(a)\circ }(v_{k_{a}}^{[m]})$
(
$\unicode[STIX]{x1D6E4}\text{}^{(a)\circ }(v_{k_{a}}^{[m]})$
(
![]() $a=1,\ldots ,i$
) on
$a=1,\ldots ,i$
) on
![]() $X_{m}^{\circ }$
form a local complete intersection for every choice of indices
$X_{m}^{\circ }$
form a local complete intersection for every choice of indices
![]() $0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant m$
, and the same holds for divisors
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant m$
, and the same holds for divisors
![]() $\unicode[STIX]{x1D6E4}\text{}^{(a)\ast }(v_{k_{a}}^{[m]})$
on
$\unicode[STIX]{x1D6E4}\text{}^{(a)\ast }(v_{k_{a}}^{[m]})$
on
![]() $X_{m}^{\ast }$
. Assume moreover that the
$X_{m}^{\ast }$
. Assume moreover that the
![]() $i$
Cartier divisors on
$i$
Cartier divisors on
![]() $X\text{}_{m}^{\circ \ast }$
:
$X\text{}_{m}^{\circ \ast }$
:
form a local complete intersection for every choice of
![]() $0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant m$
and
$0\leqslant k_{1}\leqslant \ldots \leqslant k_{i}\leqslant m$
and
![]() $\clubsuit \in \{\circ ,\ast \}$
. Then for every choice of nonempty subsets
$\clubsuit \in \{\circ ,\ast \}$
. Then for every choice of nonempty subsets
![]() $S_{1}\leqslant \ldots \leqslant S_{i}$
of
$S_{1}\leqslant \ldots \leqslant S_{i}$
of
![]() $[m]$
and
$[m]$
and
![]() $k\in [m]$
with
$k\in [m]$
with
![]() $S_{b}\leqslant \{k\}\leqslant S_{b+1}$
, the Cartier divisors on
$S_{b}\leqslant \{k\}\leqslant S_{b+1}$
, the Cartier divisors on
![]() $X\text{}_{m}^{\circ \ast }\times \Box ^{m+1}$
:
$X\text{}_{m}^{\circ \ast }\times \Box ^{m+1}$
:
form a local complete intersection, and the intersection satisfies the face condition. Consequently, their intersection product belongs to
![]() $z^{i}(X\text{}_{m}^{\circ \ast },m+1)$
.
$z^{i}(X\text{}_{m}^{\circ \ast },m+1)$
.
B.4 Bloch’s specialization map [Reference BlochBl86, page 292]
Here we give a precise argument to define the specialization map
![]() $\text{sp}_{L/k}$
in Section 2.4. Let
$\text{sp}_{L/k}$
in Section 2.4. Let
![]() $L=k(x)$
be an extension with transcendence degree
$L=k(x)$
be an extension with transcendence degree
![]() $1$
equipped with a basis
$1$
equipped with a basis
![]() $x$
. Then the presheaf
$x$
. Then the presheaf
![]() $p_{\ast }z_{\mathsf{rel},k(x)}^{i}$
on
$p_{\ast }z_{\mathsf{rel},k(x)}^{i}$
on
![]() $\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
is contained in the following presheaf
$\mathsf{MSm}^{\ast }/B\text{GL}_{r}$
is contained in the following presheaf
![]() $p_{\ast }Z_{\mathsf{rel},k(x)}^{i}$
:
$p_{\ast }Z_{\mathsf{rel},k(x)}^{i}$
:
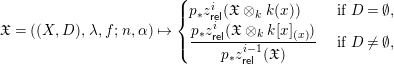 $$\begin{eqnarray}\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})\mapsto \left\{\begin{array}{@{}ll@{}}p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\,\otimes _{k}\,k(x))\quad & \text{ if }D=\emptyset ,\\ \displaystyle \frac{p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\,\otimes _{k}\,k[x]_{(x)})}{p_{\ast }z_{\mathsf{rel}}^{i-1}(\mathfrak{X})}\quad & \text{ if }D\neq \emptyset ,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{X}=((X,D),\unicode[STIX]{x1D706},f;n,\unicode[STIX]{x1D6FC})\mapsto \left\{\begin{array}{@{}ll@{}}p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\,\otimes _{k}\,k(x))\quad & \text{ if }D=\emptyset ,\\ \displaystyle \frac{p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\,\otimes _{k}\,k[x]_{(x)})}{p_{\ast }z_{\mathsf{rel}}^{i-1}(\mathfrak{X})}\quad & \text{ if }D\neq \emptyset ,\end{array}\right.\end{eqnarray}$$
where we embed
![]() $p_{\ast }z_{\mathsf{rel}}^{i-1}(\mathfrak{X})$
into
$p_{\ast }z_{\mathsf{rel}}^{i-1}(\mathfrak{X})$
into
![]() $p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\otimes _{k}k[x]_{(x)})$
by
$p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\otimes _{k}k[x]_{(x)})$
by
![]() $\{x=0\}$
. We have an obvious scalar extension map
$\{x=0\}$
. We have an obvious scalar extension map
![]() $\text{res}_{k(x)/k}$
:
$\text{res}_{k(x)/k}$
:
![]() $p_{\ast }z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }Z_{\mathsf{rel},k(x)}^{i}$
. We also consider the presheaf
$p_{\ast }z_{\mathsf{rel}}^{i}\rightarrow p_{\ast }Z_{\mathsf{rel},k(x)}^{i}$
. We also consider the presheaf
![]() $p_{\ast }z_{\mathsf{rel},k[x]_{(x)}}^{i}$
defined by
$p_{\ast }z_{\mathsf{rel},k[x]_{(x)}}^{i}$
defined by
![]() $\mathfrak{X}\mapsto p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\otimes _{k}k[x]_{(x)})$
.
$\mathfrak{X}\mapsto p_{\ast }z_{\mathsf{rel}}^{i}(\mathfrak{X}\otimes _{k}k[x]_{(x)})$
.
Now consider the sequence
For
![]() $\mathfrak{X}$
with
$\mathfrak{X}$
with
![]() $D\neq \emptyset$
, this sequence is degreewise exact for a tautological reason. If
$D\neq \emptyset$
, this sequence is degreewise exact for a tautological reason. If
![]() $D=\emptyset$
, it is acyclic as a double complex by the localization theorem [Reference BlochBl94, Theorem 0.1] (only known to be true when
$D=\emptyset$
, it is acyclic as a double complex by the localization theorem [Reference BlochBl94, Theorem 0.1] (only known to be true when
![]() $D=\emptyset$
!).
$D=\emptyset$
!).
The cycle
![]() $\unicode[STIX]{x1D6E4}_{x}=\{1+t(x-1)=0\}$
in
$\unicode[STIX]{x1D6E4}_{x}=\{1+t(x-1)=0\}$
in
![]() $\text{Spec}(k(x)[t])$
represents
$\text{Spec}(k(x)[t])$
represents
![]() $x\in k(x)^{\ast }=\text{CH}^{1}(\text{Spec}(k(x)),1)$
. Denote its closure in
$x\in k(x)^{\ast }=\text{CH}^{1}(\text{Spec}(k(x)),1)$
. Denote its closure in
![]() $\text{Spec}(k[x]_{(x)}[t])$
by
$\text{Spec}(k[x]_{(x)}[t])$
by
![]() $\bar{\unicode[STIX]{x1D6E4}}_{x}$
. The map
$\bar{\unicode[STIX]{x1D6E4}}_{x}$
. The map
![]() $\bar{\unicode[STIX]{x1D6E4}}_{x}\,\cdot \,(-)\,:\,p_{\ast }z_{\mathsf{rel},k(x)}^{i}\rightarrow p_{\ast }Z_{\mathsf{rel},k(x)}^{i+1}[-1]$
defined by
$\bar{\unicode[STIX]{x1D6E4}}_{x}\,\cdot \,(-)\,:\,p_{\ast }z_{\mathsf{rel},k(x)}^{i}\rightarrow p_{\ast }Z_{\mathsf{rel},k(x)}^{i+1}[-1]$
defined by
is a well-defined map of complexes. We define the specialization map
![]() $\text{sp}_{k(x)/k}\,:\,p_{\ast }z_{\mathsf{rel},k(x)}^{i}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}$
in
$\text{sp}_{k(x)/k}\,:\,p_{\ast }z_{\mathsf{rel},k(x)}^{i}\rightarrow p_{\ast }z_{\mathsf{rel}}^{i}$
in
![]() $D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
by the zig–zag:
$D(\mathsf{MSm}^{\ast }/B\text{GL}_{r})$
by the zig–zag:

Of course, its composition with
![]() $\text{res}_{k(x)/k}$
gives the identity map on
$\text{res}_{k(x)/k}$
gives the identity map on
![]() $p_{\ast }z_{\mathsf{rel}}^{i}$
. We leave it to the reader to verify this.
$p_{\ast }z_{\mathsf{rel}}^{i}$
. We leave it to the reader to verify this.
Remark B.5. The specialization map depends on the choice of the transcendental basis. For example, the specialization map
with respect to the basis
![]() $ax$
(
$ax$
(
![]() $a\in k^{\ast }$
) maps
$a\in k^{\ast }$
) maps
![]() $1/x$
to
$1/x$
to
![]() $a$
.
$a$
.
For a purely transcendental finitely generated extension
![]() $k(x_{1},\ldots ,x_{r})/k$
with a chosen basis, we define the specialization map by composition
$k(x_{1},\ldots ,x_{r})/k$
with a chosen basis, we define the specialization map by composition
Beware that this map depends on the order on the transcendental basis. For example, the map
![]() $\text{sp}_{k(x)/k}\circ \text{sp}_{k(x,y)/k(x)}$
:
$\text{sp}_{k(x)/k}\circ \text{sp}_{k(x,y)/k(x)}$
:
maps
![]() $ax+by$
(
$ax+by$
(
![]() $a,b\in k^{\ast }$
) to
$a,b\in k^{\ast }$
) to
![]() $a$
, while
$a$
, while
![]() $\text{sp}_{k(y)/k}\circ \text{sp}_{k(x,y)/k(y)}$
maps it to
$\text{sp}_{k(y)/k}\circ \text{sp}_{k(x,y)/k(y)}$
maps it to
![]() $b$
.
$b$
.