Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-09T10:35:47.153Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Odd Order Extensions of the Finite Simple Groups PSp(4, q), G2(q),

Published online by Cambridge University Press:  22 January 2016

Morton E. Harris
Morton E. Harris*
Affiliation:
University of Illinois at Chicago Circle
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p denote an odd prime integer and let q = pf where f is a positive integer. Let ℋ denote the projective symplectic group PSp(4,q), the Dickson group G2(q), or the Steinberg “triality twisted” group 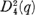over a field Fq of q elements. Then ℋ is simple and the Sylow 2-subgroups of ℋ have centers of order 2 so that involutions which centralize a Sylow 2-subgroup of ℋ form a single conjugacy class of ℋ.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 45 , February 1972 , pp. 79 - 96
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1972

References

Refereces

[1] Bender, H., Transitive Gruppen gerader Ordnung, in denen jede Involution genau einen Punkt festlässt, J. Alg. 17 (1971), 527–554.Google Scholar
[2] Carter, R.W., Simple groups and simple Lie algebras, J. London Math. Soc. 40 (1965), 193–240.Google Scholar
[3] Feit, W. and Thompson, J.G., Solvability of groups of odd order, Pacific J. Math. 13 (1963), 775–1029.Google Scholar
[4] Fong, P. and Wong, W.J., A characterization of the finite simple groups PSp(4,q), I, Nagoya Math. Journal 36 (1969), 143–184.Google Scholar
[5] Fong, P., A characterization of the finite simple groups , II, Nagoya Math. Journal 39 (1970), 39–79.Google Scholar
[6] Hall, M., “The Theory of Groups,” Macmillan, New York, 1959.Google Scholar
[7] Harris, M.E., A characterization of odd order extensions of the finite projective symplectic groups PSp(4, q), Trans. Amer. Math. Soc. 163 (1972).Google Scholar
[8] Huppert, B., “Endliche Gruppen I,” Springer-Verlag, Berlin, 1963.Google Scholar
[9] Wong, W.J., A characterization of the finite projective symplectic groups PSpA(q), Trans. Amer. Math. Soc, 139 (1969), 1–35.Google Scholar