Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
Foster, D.M.
1973.
Generalizations of nilpotence and solvability in universal classes of algebras.
Journal of Algebra,
Vol. 26,
Issue. 3,
p.
536.
Goodaire, Edgar G.
1974.
Irreducible Representations of Algebras.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 5,
p.
1118.
Stitzinger, Ernest L.
1977.
Two notes on nilpotency and standard algebras.
Proceedings of the American Mathematical Society,
Vol. 62,
Issue. 2,
p.
206.
Goodaire, Edgar G.
1978.
A classification of jordan bimodules by weights.
Communications in Algebra,
Vol. 6,
Issue. 9,
p.
887.


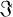 is called associator nilpotent if there exists a positive (odd) integer
is called associator nilpotent if there exists a positive (odd) integer 