Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ito, Yoshifusa
1988.
DIFFERENTIAL OPERATORS ARISING FROM TRANSLATION OF POISSON FUNCTIONALS.
Australian Journal of Statistics,
Vol. 30A,
Issue. 1,
p.
247.
Mustafid
1990.
A limit theorem of symmetric statistics for non-identically distributed independent random elements.
Hiroshima Mathematical Journal,
Vol. 20,
Issue. 1,
Mustafid
1990.
The law of small numbers and the limit theorem for symmetric statistics with mixing conditions.
Hiroshima Mathematical Journal,
Vol. 20,
Issue. 1,
Borovskikh, Yuri V.
and
Korolyuk, Vladimir S.
1994.
Random permanents and symmetric statistics.
Acta Applicandae Mathematicae,
Vol. 36,
Issue. 3,
p.
227.
Shchepanyuk, G. V.
1995.
Poisson fields and distribution functions in the statistical mechanics of charged particles.
Ukrainian Mathematical Journal,
Vol. 47,
Issue. 5,
p.
818.
Lytvynov, E.W.
Rebenko, A.L.
and
Shchepan'uk, G.V.
1996.
Wick theorems in non-Gaussian white noise calculus.
Reports on Mathematical Physics,
Vol. 37,
Issue. 2,
p.
217.
Gielerak, R.
and
Rebenko, A. L.
1996.
On the Poisson integrals representation in the classical statistical mechanics of continuous systems.
Journal of Mathematical Physics,
Vol. 37,
Issue. 7,
p.
3354.
Berezansky, Yu. M.
1997.
Infinite-dimensional analysis related to generalized translation operators.
Ukrainian Mathematical Journal,
Vol. 49,
Issue. 3,
p.
403.
Lytvynov, Eugene W.
Rebenko, Alexei L.
and
Shchepan'ur, Gennadi V.
1997.
Wick calculus on spaces of generalized functions of compound poisson white noise.
Reports on Mathematical Physics,
Vol. 39,
Issue. 2,
p.
219.
Kubo, Izumi
1997.
Stochastic Differential and Difference Equations.
p.
167.
Albeverio, S
Kondratiev, Yu.G
and
Röckner, M
1998.
Analysis and Geometry on Configuration Spaces.
Journal of Functional Analysis,
Vol. 154,
Issue. 2,
p.
444.
Berezansky, Yu. M.
1998.
Poisson infinite-dimensional analysis as an example of analysis related to generalized translation operators.
Functional Analysis and Its Applications,
Vol. 32,
Issue. 3,
p.
195.
Lytvynov, Eugene W.
1998.
A note on spaces of test and generalized functions of Poisson white noise.
Hiroshima Mathematical Journal,
Vol. 28,
Issue. 3,
Kondratiev, Yuri G.
Streit, Ludwig
Westerkamp, Werner
and
Yan, Jia-an
1998.
Generalized functions in infinite-dimensional analysis.
Hiroshima Mathematical Journal,
Vol. 28,
Issue. 2,
Lytvynov, E. W.
1998.
Differential and Integral Operators.
p.
131.
Березанский, Юрий Макарович
and
Berezanskii, Yurii Makarovich
1998.
Пуассонов бесконечномерный анализ как пример анализа, связанного с операторами обобщенного сдвига.
Функциональный анализ и его приложения,
Vol. 32,
Issue. 3,
p.
65.
SAITÔ, KIMIAKI
and
TSOI, ALLANUS H.
1999.
THE LÉVY LAPLACIAN ACTING ON POISSON NOISE FUNCTIONALS.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 02,
Issue. 04,
p.
503.
ALBEVERIO, S.
KONDRATIEV, YU. G.
and
RÖCKNER, M.
1999.
DIFFEOMORPHISM GROUPS AND CURRENT ALGEBRAS: CONFIGURATION SPACE ANALYSIS IN QUANTUM THEORY.
Reviews in Mathematical Physics,
Vol. 11,
Issue. 01,
p.
1.
KONDRATIEV, YURI G.
and
LYTVYNOV, EUGENE W.
2000.
OPERATORS OF GAMMA WHITE NOISE CALCULUS.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 03,
Issue. 03,
p.
303.
BEREZANSKY, YURIJ M.
2000.
POISSON MEASURE AS THE SPECTRAL MEASURE OF JACOBI FIELD.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 03,
Issue. 01,
p.
121.
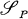 for Poisson fnnctionals with the idea as in the case of Gaussian white noise (cf. [10], [11], [12], [13]). Then we can discuss the differentiation, renormalization, multiple Wiener integrals etc. in a way completely parallel with the Gaussian case. The only one exceptional point, which is most significant, is that the multiplications are described by
for Poisson fnnctionals with the idea as in the case of Gaussian white noise (cf. [10], [11], [12], [13]). Then we can discuss the differentiation, renormalization, multiple Wiener integrals etc. in a way completely parallel with the Gaussian case. The only one exceptional point, which is most significant, is that the multiplications are described by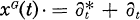 for the Gaussian case,
for the Gaussian case, for the Poisson case,
for the Poisson case,

