Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T12:56:29.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Buchsbaumness in local rings possessing constant first Hilbert coefficients of parameters

Published online by Cambridge University Press:  11 January 2016

Shiro Goto  and
Kazuho Ozeki
Shiro Goto
Affiliation:
Department of Mathematics, School of Science and Technology, Meiji University, Kawasaki 214-8571, Japan, [email protected]
Kazuho Ozeki
Affiliation:
Department of Mathematics, School of Science and Technology, Meiji University, Kawasaki 214-8571, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (A,m) be a Noetherian local ring with d = dim A ≥ 2. Then, if A is a Buchsbaum ring, the first Hilbert coefficients 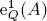of A for parameter ideals Q are constant and equal to 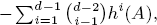where hi(A) denotes the length of the ith local cohomology module 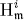of A with respect to the maximal ideal m. This paper studies the question of whether the converse of the assertion holds true, and proves that A is a Buchsbaum ring if A is unmixed and the values 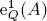are constant, which are independent of the choice of parameter ideals Q in A. Hence, a conjecture raised by [GhGHOPV] is settled affirmatively.

Keywords

13H1013A3013B2213H15
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 199 , September 2010 , pp. 95 - 105
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2010

References

[GhGHOPV] Ghezzi, L., Goto, S., Hong, J., Ozeki, K., Phuong, T. T., and Vasconcelos, W. V., Cohen-Macaulayness versus the vanishing of the first Hilbert coefficient of parameter ideals, J. London Math. Soc. (2) 81 (2010), 679–695.CrossRefGoogle Scholar
[GhHV] Ghezzi, L., Hong, J.-Y., and Vasconcelos, W. V., The signature of the Chern coefficients of local rings, Math. Res. Lett. 16 (2009), 279–289.CrossRefGoogle Scholar
[G] Goto, S., On Buchsbaum rings, J. Algebra 67 (1980), 272–279.CrossRefGoogle Scholar
[GNi] Goto, S. and Nishida, K., Hilbert coefficients and Buchsbaumness of associated graded rings, J. Pure Appl. Algebra 181 (2003), 61–74.CrossRefGoogle Scholar
[H] Huneke, C., The theory of d-sequences and powers of ideals, Adv. in Math. 46 (1982), 249–279.CrossRefGoogle Scholar
[MV] Mandal, M. and Verma, J. K., On the Chern number of an ideal, Proc. Amer. Math. Soc. 138 (2010), 1995–1999.CrossRefGoogle Scholar
[Sch] Schenzel, P., Multiplizitäten in verallgemeinerten Cohen-Macaulay-Moduln, Math. Nachr. 88 (1979), 295–306.CrossRefGoogle Scholar
[STC] Schenzel, P., Trung, N. V., and Cuong, N. T., Verallgemeinerte Cohen-Macaulay-Moduln, Math. Nachr. 85 (1978), 57–73.CrossRefGoogle Scholar
[SV] Stückrad, J. and Vogel, W., Buchsbaum Rings and Applications, Springer, Berlin, 1986.CrossRefGoogle Scholar
[T] Trung, N. V., Toward a theory of generalized Cohen-Macaulay modules, Nagoya Math. J. 102 (1986), 1–49.CrossRefGoogle Scholar
[V] Vasconcelos, W. V., The Chern coefficients of local rings, Mich. Math. J. 57 (2008), 725–743.CrossRefGoogle Scholar