Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nahid, Tabinda
Alam, Parvez
and
Choi, Junesang
2020.
Truncated-Exponential-Based Appell-Type Changhee Polynomials.
Symmetry,
Vol. 12,
Issue. 10,
p.
1588.


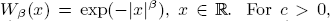 , define
, define 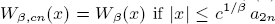 and
and 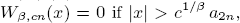 where
where 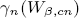 be the leading coefficients of the
be the leading coefficients of the  . It is shown that if c > 1 and β is a positive even integer then
. It is shown that if c > 1 and β is a positive even integer then 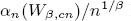 has an asymptotic expansion. Also when
has an asymptotic expansion. Also when 