Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T20:12:32.756Z Has data issue: false hasContentIssue false
  • English
  • Français

An Investigation on the Logical Structure of Mathematics (III)0): Fundamental Deductions

Published online by Cambridge University Press:  22 January 2016

Sigekatu Kuroda
Sigekatu Kuroda*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this Part (III) the proofs in UL are given for fundamental formulas concerning the following dependent variables:

  • Elementary set {a1, … , an};

  • Ordered pair ‹a, b›;

  • Image by σ of aσ‘a;

  • Image by σ of elements of aσ“a;

  • Domain of operator Dσ;

  • Range of operator Wσ;

  • Uniqueness Un;

  • Bi-uniqueness Un2;

  • Inverse operator σ-1;

  • One-to-one mapping Map2a, b;

  • Composition of operators σ o τ;

  • Restriction of operator

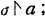
  • Identical mapping ℓ

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 13 , June 1958 , pp. 21 - 52
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1958

Footnotes

0)

See foot note 0) in Part (IV) published in this same volume.

References

1) 〈a, b〉 is also written as 〈ab〉.

2) σ’a as well σ“a are also written in the same way as aσ , when the distinction is clear by the context.

3) Cf. Part (VI).

4) What dependent variables are used as sets (see Part (X)) can be seen from each proof, although we do not list up in each case. Such a list is needed, for instance, in the observation of Burali-Forti’s contradiction.

5) Impossible in the sense precisely formulated and proved by Gödel. Moreover, if there were a criterion for any premise σ of UL to be consistent or inconsistent, then either the proof for the criterion could be, after Gödel mapping, formalized in UL and the premise Π of the formalized proof for the criterion would turn out to be inconsistent by the criterion itself, or UL would be still narrow enough to formalize our logical thought. This would mean almost absolute impossibility of such criterion; or else, the criterion or the proof for it would be expressed by means of such part of intuitive logic or mathematics that would be susceptible of no formalization.

6) See Part (IV); Compendium for deductions, contained in this same volume.