Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
De Meyer, Bernard
Roynette, Bernard
Vallois, Pierre
and
Yor, Marc
2001.
Sur l'indépendance d'un temps d'arrêt T et de la position BT d'un mouvement brownien.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 333,
Issue. 11,
p.
1017.
Baudoin, Fabrice
2002.
Further Exponential Generalization of Pitman's $2M-X$ Theorem.
Electronic Communications in Probability,
Vol. 7,
Issue. none,
Matsumoto, Hiroyuki
and
Yor, Marc
2003.
Interpretation via Brownian motion of some independence properties between GIG and gamma variables.
Statistics & Probability Letters,
Vol. 61,
Issue. 3,
p.
253.
Matsumoto, Hiroyuki
and
Yor, Marc
2003.
On Dufresne's relation between the probability laws of exponential functionals of Brownian motions with different drifts.
Advances in Applied Probability,
Vol. 35,
Issue. 1,
p.
184.
Matsumoto, Hiroyuki
and
Yor, Marc
2003.
On Dufresne's relation between the probability laws of exponential functionals of Brownian motions with different drifts.
Advances in Applied Probability,
Vol. 35,
Issue. 1,
p.
184.
Linetsky, Vadim
2004.
The spectral representation of Bessel processes with constant drift: applications in queueing and finance.
Journal of Applied Probability,
Vol. 41,
Issue. 02,
p.
327.
Hariya, Yuu
and
Yor, Marc
2004.
On an extension of Dufresne's relation between exponential Brownian functionals from opposite drifts to two different drifts: a short proof.
Statistics & Probability Letters,
Vol. 67,
Issue. 4,
p.
331.
Linetsky, Vadim
2004.
The spectral representation of Bessel processes with constant drift: applications in queueing and finance.
Journal of Applied Probability,
Vol. 41,
Issue. 2,
p.
327.
Dufresne, Daniel
2005.
Numerical Methods in Finance.
p.
35.
Salminen, Paavo
and
Yor, Marc
2005.
Perpetual Integral Functionals as Hitting and Occupation Times.
Electronic Journal of Probability,
Vol. 10,
Issue. none,
Roynette, Bernard
Vallois, Pierre
and
Yor, Marc
2007.
Some extensions of Pitman and Ray-Knight theorems for penalized Brownian motions and their local times, IV.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 44,
Issue. 4,
p.
469.
Roynette, Bernard
Vallois, Pierre
and
Yor, Marc
2008.
Penalizing a BES ( d ) process (0 < d < 2) with a function of its local time, V.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 45,
Issue. 1,
p.
67.
Matsumoto, Hiroyuki
Wesołowski, Jacek
and
Witkowski, Piotr
2009.
Tree structured independence for exponential Brownian functionals.
Stochastic Processes and their Applications,
Vol. 119,
Issue. 10,
p.
3798.
Hirsch, F.
and
Yor, M.
2009.
Fractional Intertwinings Between Two Markov Semigroups.
Potential Analysis,
Vol. 31,
Issue. 2,
p.
133.
Katori, Makoto
2011.
O’Connell's process as a vicious Brownian motion.
Physical Review E,
Vol. 84,
Issue. 6,
Biane, Philippe
2011.
Entrelacements de semi-groupes provenant de paires de Gelfand.
ESAIM: Probability and Statistics,
Vol. 15,
Issue. ,
p.
S2.
Katori, Makoto
2012.
Survival Probability of Mutually Killing Brownian Motions and the O’Connell Process.
Journal of Statistical Physics,
Vol. 147,
Issue. 1,
p.
206.
Katori, Makoto
2012.
Reciprocal Time Relation of Noncolliding Brownian Motion with Drift.
Journal of Statistical Physics,
Vol. 148,
Issue. 1,
p.
38.
O’Connell, Neil
2012.
Directed polymers and the quantum Toda lattice.
The Annals of Probability,
Vol. 40,
Issue. 2,
Katori, Makoto
2012.
System of Complex Brownian Motions Associated with the O’Connell Process.
Journal of Statistical Physics,
Vol. 149,
Issue. 3,
p.
411.


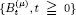 be a one-dimensional Brownian motion with constant drift
be a one-dimensional Brownian motion with constant drift 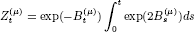
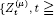 and, in particular, its relation to the generalized Bessel processes.
and, in particular, its relation to the generalized Bessel processes.