Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T12:33:18.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternative polarizations of Borel fixed ideals

Published online by Cambridge University Press:  11 January 2016

Kohji Yanagawa
Kohji Yanagawa*
Affiliation:
Department of Mathematics, Kansai University, Suita 564-8680, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a monomial ideal I of a polynomial ring S, a polarization of I is a square-free monomial ideal J of a larger polynomial ring 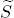such that S/I is a quotient of 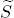/J by a (linear) regular sequence. We show that a Borel fixed ideal admits a nonstandard polarization. For example, while the usual polarization sends 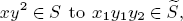ours sends it to x1y2y3 Using this idea, we recover/refine the results on square-free operation in the shifting theory of simplicial complexes. The present paper generalizes a result of Nagel and Reiner, although our approach is very different.

Keywords

13C1313P0513F55
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 207 , September 2012 , pp. 79 - 93
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2012

References

[1] Aramova, A., Herzog, J., and Hibi, T., Squarefree lexsegment ideals, Math. Z. 228 (1998), 353–378.Google Scholar
[2] Aramova, A., Herzog, J., and Hibi, T., Shifting operations and graded Betti numbers, J. Algebraic Combin. 12 (2000), 207–222.CrossRefGoogle Scholar
[3] Björner, A. and Wachs, M. L., Shellable nonpure complexes and posets, II, Trans. Amer. Math. Soc. 349 (1997), 3945–3975.CrossRefGoogle Scholar
[4] Bruns, W. and Herzog, J., Cohen-Macaulay Rings, rev. ed., Cambridge University Press, Cambridge, 1998.Google Scholar
[5] Eisenbud, D., Commutative Algebra: With a View Toward Algebraic Geometry, Grad. Texts in Math. 150, Springer, New York, 1995.Google Scholar
[6] Herzog, J. and Popescu, D., Finite filtrations of modules and shellable multicomplexes, Manuscripta Math. 121 (2006), 385–410.Google Scholar
[7] Kalai, G., “Algebraic shifting” in Computational Commutative Algebra and Combinatorics (Osaka. 1999), Adv. Stud. Pure Math. 33, Math. Soc. Japan, Tokyo, 2002, 121–163.CrossRefGoogle Scholar
[8] Lohne, H., Polarizations of powers of the maximal ideal in a polynomial ring, in preparation.Google Scholar
[9] Murai, S., Generic initial ideals and squeezed spheres, Adv. Math. 214 (2007), 701–729.Google Scholar
[10] Nagel, U. and Reiner, V., Betti numbers of monomial ideals and shifted skew shapes, Electron. J. Combin. 16 (2009), Research Paper 3.Google Scholar
[11] Sbarra, E., Upper bounds for local cohomology for rings with given Hilbert function, Comm. Algebra 29 (2001), 5383–5409.Google Scholar
[12] Stanley, R., Combinatorics and Commutative Algebra, 2nd ed., Progr. Math. 41, Birkhäuser, Boston 1996.Google Scholar
[13] Yanagawa, K., Sliding functor and polarization functor for multigraded modules, Comm. Algebra, 40 (2012), 1151–1166.Google Scholar