Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Songxiao
and
Stević, Stevo
2007.
Riemann–Stieltjes-type integral operators on the unit ball in.
Complex Variables and Elliptic Equations,
Vol. 52,
Issue. 6,
p.
495.
Stević, Stevo
2008.
Generalized Composition Operators Between Mixed-Norm and Some Weighted Spaces.
Numerical Functional Analysis and Optimization,
Vol. 29,
Issue. 7-8,
p.
959.
Ли, Сонгсиао
Li, Songxiao
Стевич, Стево
and
Stevic, Stevo
2008.
Дифференцирование суперпозиции как оператор из пространств со смешанной нормой в $\alpha$-пространства Блоха.
Математический сборник,
Vol. 199,
Issue. 12,
p.
117.
Stević, Stevo
2008.
On a new operator from the logarithmic Bloch space to the Bloch-type space on the unit ball.
Applied Mathematics and Computation,
Vol. 206,
Issue. 1,
p.
313.
Stević, Stevo
and
Berezansky, Leonid
2008.
On a New Integral‐Type Operator from the Weighted Bergman Space tothe Bloch‐Type Space on the Unit Ball.
Discrete Dynamics in Nature and Society,
Vol. 2008,
Issue. 1,
Stević, Stevo
2009.
Norms of some operators on the Bergman and the Hardy space in the unit polydisk and the unit ball.
Applied Mathematics and Computation,
Vol. 215,
Issue. 6,
p.
2199.
Stević, Stevo
2009.
On an integral-type operator from logarithmic Bloch-type and mixed-norm spaces to Bloch-type spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 12,
p.
6323.
Avetisyan, Karen
and
Stević, Stevo
2009.
The generalized Libera transform is bounded on the Besov mixed-norm, BMOA and VMOA spaces on the unit disc.
Applied Mathematics and Computation,
Vol. 213,
Issue. 2,
p.
304.
Stević, Stevo
2009.
Integral-type operators from a mixed norm space to a bloch-type space on the unit ball.
Siberian Mathematical Journal,
Vol. 50,
Issue. 6,
p.
1098.
Li, Songxiao
and
Stević, Stevo
2009.
Integral-type operators from Bloch-type spaces to Zygmund-type spaces.
Applied Mathematics and Computation,
Vol. 215,
Issue. 2,
p.
464.
Li, Songxiao
2009.
Generalized Hilbert operator on the Dirichlet-type space.
Applied Mathematics and Computation,
Vol. 214,
Issue. 1,
p.
304.
Li, Songxiao
and
Stević, Stevo
2009.
Cesàro-type operators on some spaces of analytic functions on the unit ball.
Applied Mathematics and Computation,
Vol. 208,
Issue. 2,
p.
378.
Avetisyan, Karen
and
Stević, Stevo
2009.
Extended Cesàro operators between different Hardy spaces.
Applied Mathematics and Computation,
Vol. 207,
Issue. 2,
p.
346.
Krantz, Steven G.
and
Stević, Stevo
2009.
On the iterated logarithmic Bloch space on the unit ball.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 5-6,
p.
1772.
Stević, Stevo
2010.
On an integral operator between Bloch-type spaces on the unit ball.
Bulletin des Sciences Mathématiques,
Vol. 134,
Issue. 4,
p.
329.
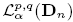 , where p, q> 0, α = (α1,…,αn) with αj > -1, j =1,..., n, be the class of all measurable functions f defined on Dn such that
, where p, q> 0, α = (α1,…,αn) with αj > -1, j =1,..., n, be the class of all measurable functions f defined on Dn such that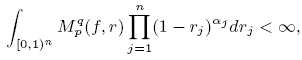
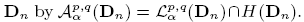 . We provide a characterization for a function f being in
. We provide a characterization for a function f being in 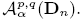 . Using the characterization we prove the following result: Let p> 1, then the Cesàro operator is bounded on the space
. Using the characterization we prove the following result: Let p> 1, then the Cesàro operator is bounded on the space 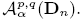 .
.

