Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-20T05:31:39.674Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES

Part of: Curves Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  02 December 2024

RACHEL PRIES Open the ORCID record for RACHEL PRIES [Opens in a new window]
RACHEL PRIES*
Affiliation:
Department of Mathematics Colorado State University Fort Collins CO 80523 United States
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper contains a method to prove the existence of smooth curves in positive characteristic whose Jacobians have unusual Newton polygons. Using this method, I give a new proof that there exist supersingular curves of genus 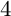$4$ in every prime characteristic. More generally, the main result of the paper is that, for every 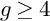$g \geq 4$ and prime p, every Newton polygon whose p-rank is at least 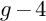$g-4$ occurs for a smooth curve of genus g in characteristic p. In addition, this method resolves some cases of Oort’s conjecture about Newton polygons of curves.

Keywords

CurveJacobianmoduli spaceNewton polygonsupersingular

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$ 11G20: Curves over finite and local fields 11M38: Zeta and $L$-functions in characteristic $p$ 14H10: Families, moduli (algebraic) 14H40: Jacobians, Prym varieties
Secondary: 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture) 14G15: Finite ground fields
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Achter, J. D. and Pries, R., “Generic Newton polygons for curves of given p-rank” in Algebraic curves and finite fields, Radon Series on Computational and Applied Mathematics, Vol. 16, De Gruyter, Berlin, 2014, pp. 1–21. MR3287680Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], Vol. 21, Springer-Verlag, Berlin, 1990. MR1045822 (91i:14034)CrossRefGoogle Scholar
Chai, C.-L. and Oort, F., Monodromy and irreducibility of leaves , Ann. Math. (2) 173 (2011), no. 3, 1359–1396. MR2800716CrossRefGoogle Scholar
de Jong, A. J. and Oort, F., Purity of the stratification by Newton polygons , J. Amer. Math. Soc. 13 (2000), no. 1, 209–241. MR1703336CrossRefGoogle Scholar
Faber, C. and van der Geer, G., Complete subvarieties of moduli spaces and the Prym map , J. Reine Angew. Math. 573 (2004), 117–137. MR2084584Google Scholar
Harashita, S., Supersingular abelian varieties and curves, and their moduli spaces, with a remark on the dimension of the moduli of supersingular curves of genus 4, Theory and Applications of Supersingular Curves and Supersingular Abelian Varieties, RIMS Kôkyûroku Bessatsu, Vol. B90, Research Institute for Mathematical Sciences, Kyoto, 2022, pp. 1–16. MR4521510Google Scholar
Kudo, M., Harashita, S. and Senda, H., The existence of supersingular curves of genus 4 in arbitrary characteristic , Res. Number Theory 6 (2020), no. 4, Paper No. 44, 17 pp. MR4170348CrossRefGoogle Scholar
Li, W., Mantovan, E., Pries, R. and Tang, Y., Newton polygons arising from special families of cyclic covers of the projective line , Res. Number Theory 5 (2019), no. 1, Paper No. 12, 31 pp. MR3897613CrossRefGoogle Scholar
Li, W., Mantovan, E., Pries, R. and Tang, Y., “Newton polygons of cyclic covers of the projective line branched at three points” in Research directions in number theory—Women in Numbers IV, Association for Women in Mathematics Series, Vol. 19, Springer, Cham, [2019] ©2019, pp. 115–132. MR4069381Google Scholar
Li, K.-Z. and Oort, F., Moduli of supersingular abelian varieties, Lecture Notes in Mathematics, Vol. 1680, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar
Manin, J. I., Theory of commutative formal groups over fields of finite characteristic , Uspehi Mat. Nauk 18 (1963), no. 6 (114), 3–90. MR0157972Google Scholar
Oort, F., “Hyperelliptic supersingular curves” in Arithmetic algebraic geometry (Texel, 1989), Progress in Mathematics, Vol. 89, Birkhäuser Boston, Boston, MA, 1991, pp. 247–284. MR1085262CrossRefGoogle Scholar
Oort, F., “Newton polygon strata in the moduli space of abelian varieties” in Moduli of abelian varieties (Texel Island, 1999), Progress in Mathematics, Vol. 195, Birkhäuser, Basel, 2001, pp. 417–440. MR1827028Google Scholar
Oort, F., Abelian varieties isogenous to a Jacobian (Cornelissen, G. and Oort, F., eds.), Problems from the Workshop on Automorphisms of Curves, Vol. 113 2005, pp. 129–177. MR2168985 (2006d:14027)Google Scholar
Oort, F., “Newton polygons and p-divisible groups: a conjecture by Grothendieck” in Automorphic forms. I, Astérisque, Vol. 298, 2005, Société Mathématique de France, Paris, pp. 255–269. MR2141704Google Scholar
Pries, R., “Current results on Newton polygons of curves” in Open problems in arithmetic algebraic geometry, Advanced Lectures in Mathematics, Vol. 46, International Press, Somerville, MA, 2019, pp. 179–207. MR3971184Google Scholar
Vistoli, A., Intersection theory on algebraic stacks and on their moduli spaces , Invent. Math. 97 (1989), no. 3, 613–670. MR1005008 (90k:14004)CrossRefGoogle Scholar