Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-30T16:53:54.706Z Has data issue: false hasContentIssue false
  • English
  • Français

NONUNIFORMLY FLAT AFFINE ALGEBRAIC HYPERSURFACES

Part of: Differential operators in several variables Pluripotential theory Holomorphic functions of several complex variables

Published online by Cambridge University Press:  02 April 2019

VAMSI PRITHAM PINGALI  and
DROR VAROLIN
VAMSI PRITHAM PINGALI
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore - 560012, India email [email protected]
DROR VAROLIN
Affiliation:
Department of Mathematics, Stony Brook University, Stony Brook, NY 11794-3651, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The relationship between interpolation and separation properties of hypersurfaces in Bargmann–Fock spaces over 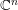$\mathbb{C}^{n}$ is not well understood except for 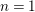$n=1$. We present four examples of smooth affine algebraic hypersurfaces that are not uniformly flat, and show that exactly two of them are interpolating.

MSC classification

Primary: 32A36: Bergman spaces 32U05: Plurisubharmonic functions and generalizations 32W50: Other partial differential equations of complex analysis
Type
Article
Information
Nagoya Mathematical Journal , Volume 241 , March 2021 , pp. 1 - 43
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Vamsi Pritham Pingali is partially supported by the Young Investigator Award and by grant F.510/25/CAS-II/2018(SAP-I) from UGC (Govt. of India).

References

Berndtsson, B. and Ortega-Cerdá, J., On interpolation and sampling in Hilbert spaces of analytic functions, J. Reine Angew. Math. 464 (1995), 109–128.Google Scholar
Gröchenig, K., Haimi, A., Ortega-Cerdá, J. and Romero, J.-L., Strict density inequalities for smapling and interpolation in weighted spaces of holomorphic functions, preprint, 2018, arXiv:1808.02703v1 [math.CA], https://arxiv.org/pdf/1808.02703.pdf.Google Scholar
Lindholm, N., Sampling in weighted L p spaces of entire functions in ℂn and estimates of the Bergman kernel, J. Funct. Anal. 182(2) (2001), 390–426.10.1006/jfan.2000.3733Google Scholar
Ohsawa, T. and Takegoshi, K., On the extension of L 2 holomorphic functions, Math. Z. 195(2) (1987), 197–204.10.1007/BF01166457Google Scholar
Ortega-Cerdá, J., Interpolating and sampling sequences in finite Riemann surfaces, Bull. Lond. Math. Soc. 40(5) (2008), 876–886.10.1112/blms/bdn071Google Scholar
Ortega-Cerdà, J., Schuster, A. and Varolin, D., Interpolation and sampling hypersurfaces for the Bargmann–Fock space in higher dimensions, Math. Ann. 335(1) (2006), 79–107.10.1007/s00208-005-0726-3Google Scholar
Ortega-Cerdà, J. and Seip, K., Beurling-type density theorems for weighted L p spaces of entire functions, J. Anal. Math. 75 (1998), 247–266.10.1007/BF02788702Google Scholar
Pingali, V. and Varolin, D., Bargmann–Fock extension from singular hypersurfaces, J. Reine Angew. Math. 717 (2016), 227–249.Google Scholar
Schuster, A. and Varolin, D., Interpolation and sampling for generalized Bergman spaces on finite Riemann surfaces, Rev. Mat. Iberoam. 24(2) (2008), 499–530.10.4171/RMI/544Google Scholar
Seip, K., Density theorems for sampling and interpolation in the Bargmann–Fock space. I, J. Reine Angew. Math. 429 (1992), 91–106.Google Scholar
Seip, K., Beurling type density theorems in the unit disk, Invent. Math. 113(1) (1993), 21–39.10.1007/BF01244300Google Scholar
Seip., K. and Wallsén, R., Density theorems for sampling and interpolation in the Bargmann-Fock space. II, J. Reine Angew. Math. 429 (1992), 107–113.Google Scholar
Varolin, D., A Takayama-type extension theorem, Compos. Math. 144(2) (2008), 522–540.10.1112/S0010437X07002989Google Scholar
Varolin, D., Bergman interpolation on finite Riemann surfaces. Part II: Poincaré-hyperbolic case, Math. Ann. 366(3–4) (2016), 1137–1193.10.1007/s00208-015-1344-3Google Scholar
Varolin, D., Bergman interpolation on finite Riemann surfaces. Part I: Asymptotically flat case, J. Anal. Math. 136(1) (2018), 103–149.10.1007/s11854-018-0057-4Google Scholar