Article contents
COMPACT ORBITS OF PARABOLIC SUBGROUPS
Published online by Cambridge University Press: 14 December 2021
Abstract
We study the action of a real reductive group G on a real submanifold X of a Kähler manifold Z. We suppose that the action of a compact connected Lie group U with Lie algebra
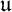 $\mathfrak {u}$
extends holomorphically to an action of the complexified group
$\mathfrak {u}$
extends holomorphically to an action of the complexified group
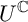 $U^{\mathbb {C}}$
and that the U-action on Z is Hamiltonian. If
$U^{\mathbb {C}}$
and that the U-action on Z is Hamiltonian. If
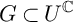 $G\subset U^{\mathbb {C}}$
is compatible, there exists a gradient map
$G\subset U^{\mathbb {C}}$
is compatible, there exists a gradient map
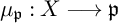 $\mu _{\mathfrak p}:X \longrightarrow \mathfrak p$
where
$\mu _{\mathfrak p}:X \longrightarrow \mathfrak p$
where
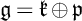 $\mathfrak g=\mathfrak k \oplus \mathfrak p$
is a Cartan decomposition of
$\mathfrak g=\mathfrak k \oplus \mathfrak p$
is a Cartan decomposition of
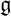 $\mathfrak g$
. In this paper, we describe compact orbits of parabolic subgroups of G in terms of the gradient map
$\mathfrak g$
. In this paper, we describe compact orbits of parabolic subgroups of G in terms of the gradient map
 $\mu _{\mathfrak p}$
.
$\mu _{\mathfrak p}$
.
MSC classification
- Type
- Article
- Information
- Copyright
- © (2021) The Authors. Copyright in the Journal, as distinct from the individual articles, is owned by Foundation Nagoya Mathematical Journal
Footnotes
Biliotti was partially supported by the Project PRIN 2015, Real and Complex Manifolds: Geometry, Topology and Harmonic Analysis, by the Project PRIN 2017, Real and Complex Manifolds: Topology, Geometry and Holomorphic Dynamics, and by the GNSAGA INdAM.
References
- 1
- Cited by



