Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-20T07:23:22.623Z Has data issue: false hasContentIssue false
  • English
  • Français

BIGNESS OF THE TANGENT BUNDLE OF A FANO THREEFOLD WITH PICARD NUMBER TWO

Part of: Surfaces and higher-dimensional varieties Birational geometry

Published online by Cambridge University Press:  27 December 2024

HOSUNG KIM Open the ORCID record for HOSUNG KIM [Opens in a new window] ,
JEONG-SEOP KIM Open the ORCID record for JEONG-SEOP KIM [Opens in a new window]  and
YONGNAM LEE Open the ORCID record for YONGNAM LEE [Opens in a new window]
HOSUNG KIM
Affiliation:
Department of Mathematics Changwon National University 20 Changwondaehak-ro, Uichang-gu Changwon-si, Gyeongsangnam-do, 51140 Korea [email protected]
JEONG-SEOP KIM*
Affiliation:
School of Mathematics Korea Institute for Advanced Study (KIAS) 85 Hoegiro, Dongdaemun-gu Seoul, 02455 Korea
YONGNAM LEE
Affiliation:
Center for Complex Geometry Institute for Basic Science (IBS) 5 Expo-ro, Yuseong-gu Daejeon, 34126, and Department of Mathematical Sciences KAIST 291 Daehak-ro, Yuseong-gu Daejeon, 34141 Korea [email protected]
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the positivity property of the tangent bundle $T_X$ of a Fano threefold X with Picard number $2$. We determine the bigness of the tangent bundle of the whole 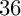$36$ deformation types. Our result shows that 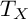$T_X$ is big if and only if $(-K_X)^3\ge 34$. As a corollary, we prove that the tangent bundle is not big when X has a standard conic bundle structure with non-empty discriminant. Our main methods are to produce irreducible effective divisors on 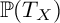${\mathbb {P}}(T_X)$ constructed from the total dual VMRT associated to a family of rational curves. Additionally, we present some criteria to determine the bigness of 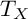$T_X$.

Keywords

Fano threefoldconic bundletotal dual VMRTtangent bundle

MSC classification

Primary: 14J45: Fano varieties 14J30: $3$-folds 14E30: Minimal model program (Mori theory, extremal rays)
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Batyrev, V. V., Toroidal Fano 3-folds , Math. USSR Izvestija 19 (1982), no. 1, 13–25.CrossRefGoogle Scholar
Bernardara, M. and Bolognesi, M., Derived categories and rationality of conic bundles , Compositio Math. 149 (2013), no. 11, 1789–1817.CrossRefGoogle Scholar
Furushima, M. and Nakayama, N., The family of lines on the Fano threefold ${V}_5$ , Nagoya Math. J. 116 (1989), 111–122.CrossRefGoogle Scholar
Höring, A. and Liu, J., Fano manifolds with big tangent bundle: A characterisation of ${V}_5$ , Collect. Math. 74 (2023), no. 3, 639–686.CrossRefGoogle Scholar
Höring, A., Liu, J. and Shao, F., Examples of Fano manifolds with non-pseudoeffective tangent bundle , J. Lond. Math. Soc. (2) 106 (2022), no. 1, 27–59.CrossRefGoogle Scholar
Hsiao, J.-C., A remark on bigness of the tangent bundle of a smooth projective variety and $D$ -simplicity of its section rings , J. Algebra Appl. 14 (2015), no. 7, 1550098.CrossRefGoogle Scholar
Hwang, J.-M. and Kim, H., Varieties of minimal rational tangents on Veronese double cones , Algebr. Geom. 2 (2015), no. 2, 176–192.CrossRefGoogle Scholar
Hwang, J.-M. and Ramanan, S., Hecke curves and Hitchin discriminant , Ann. Sci. École Norm. Sup. (4) 37 (2004), no. 5, 801–817.CrossRefGoogle Scholar
Iliev, A., The Fano surface of the Gushel threefold , Compositio Math. 94 (1994), no. 1, 81–107.Google Scholar
Iskovskikh, V. A., On the rationality problem for conic bundles , Duke Math. J. 54 (1987), no. 2, 271–294.CrossRefGoogle Scholar
Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, Vol. 32, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Maruyama, M., “Elementary transformations in the theory of algebraic vector bundles” in Algebraic geometry (La Rábida, 1981), Lecture Notes in Mathematics, Vol. 961, Springer, Berlin, 1982, pp. 241–266.CrossRefGoogle Scholar
Mori, S. and Mukai, S., Classification of Fano $3$ -folds with ${B}_2\ge 2$ , Manuscripta Math. 36 (1981), no. 2, 147–162.CrossRefGoogle Scholar
Mori, S. and Mukai, S., “On Fano 3-folds with B 2 ≥ 2” in Algebraic varieties and analytic varieties (Tokyo, 1981), Advanced Studies in Pure Mathematics, Vol. 1, North-Holland, Amsterdam, 1983, pp. 101–129.CrossRefGoogle Scholar
Occhetta, G., Solá Conde, L. E. and Watanabe, K., Uniform families of minimal rational curves on Fano manifolds , Rev. Mat. Complut. 29 (2016), no. 2, 423–437.CrossRefGoogle Scholar
Prokhorov, Yu. G., The rationality problem for conic bundles , Russian Math. Surveys 73 (2018), no. 3, 375–456.CrossRefGoogle Scholar
Przyjalkowski, V. V., Cheltsov, I. A. and Shramov, K. A., Fano threefolds with infinite automorphism groups , Izv. Math. 83 (2019), no. 4, 860–907.CrossRefGoogle Scholar
Shao, F., On pseudoeffective thresholds and cohomology of twisted symmetric tensor fields on irreducible Hermitian symmetric spaces, Sci. China Math. 67 (2024), no. 11, 2433–2452.Google Scholar
Solá Conde, L. E. and Wiśniewski, J. A., On manifolds whose tangent bundle is big and 1-ample , Proc. Lond. Math. Soc. (3) 89 (2004), no. 2, 273–290.CrossRefGoogle Scholar
Szurek, M. and Wiśniewski, J. A., Fano bundles of rank 2 on surfaces , Compositio Math. 76 (1990), nos. 1–2, 295–305.Google Scholar