Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-03T08:39:33.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Dislocation-density kinematics: a simple evolution equation for dislocation density involving movement and tilting of dislocations

Published online by Cambridge University Press:  17 August 2017

A.H.W. Ngan
A.H.W. Ngan*
Affiliation:
Department of Mechanical Engineering, The University of Hong Kong, Pokfulam Road, Hong Kong, People's Republic of China
*
Address all correspondence to A.H.W. Ngan at [email protected]
Get access

Abstract

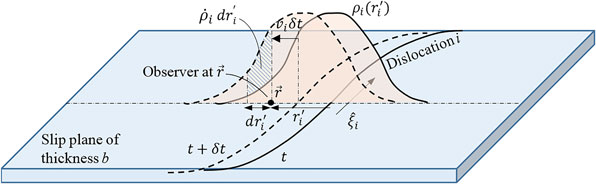
In this paper, a simple evolution equation for dislocation densities moving on a slip plane is proven. This equation gives the time evolution of dislocation density at a general field point on the slip plane, due to the approach of new dislocations and tilting of dislocations already at the field point. This equation is fully consistent with Acharya's evolution equation and Hochrainer et al.’s “continuous dislocation dynamics” (CDD) theory. However, it is shown that the variable of dislocation curvature in CDD is unnecessary if one considers one-dimensional flux divergence along the dislocation velocity direction.

Type
Research Letters
Information
MRS Communications , Volume 7 , Issue 3 , September 2017 , pp. 583 - 590
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Acharya, A.: A model of crystal plasticity based on the theory of continuously distributed dislocations. J. Mech. Phys. Solids 49, 761 (2001).Google Scholar
2.El-Azab, A.: Statistical mechanics treatment of the evolution of dislocation distributions in single crystals. Phys. Rev. B 61, 11956 (2000).Google Scholar
3.Sedláček, R., Kratochvil, J. and Werner, E.: The importance of being curved: bowing dislocations in a continuum description. Philos. Mag. 83, 3735 (2003).Google Scholar
4.Hochrainer, T., Zaiser, M. and Gumbsch, P.: A three-dimensional continuum theory of dislocation systems: kinematics and mean-field formulation. Philos. Mag. 87, 1261 (2007).Google Scholar
5.Nye, J.F.: Some geometrical relations in dislocated crystals. Acta Metal. 1, 153 (1953).Google Scholar
6.Kröner, E.: Kontinuumstheorie der Versetzungen und Eigenspannungen (Springer, Berlin, 1958).Google Scholar
7.Leung, H.S. and Ngan, A.H.W.: Dislocation-density function dynamics—an all-dislocation, full-dynamics approach for modeling intensive dislocation structures. J. Mech. Phys. Solids 91, 172 (2016).Google Scholar
8.Acharya, A. and Roy, A.: Size effects and idealized dislocation microstructure at small scales: Predictions of a phenomenological mode of mesoscopic field dislocation mechanics: Part I. J. Mech. Phys. Solids 54, 1687 (2006).Google Scholar
9.Taupin, V., Varadhan, S., Fressengeas, C. and Beaudoin, A.J.: Directionality of yield point in strain-aged steels: The role of polar dislocations. Acta Mater. 56, 3002 (2008).Google Scholar