Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-30T23:31:35.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Polymer Chains Under Strong Flow: Stems and Flowers

Published online by Cambridge University Press:  29 November 2013

F. Brochard-Wyart  and
A. Buguin
Get access

Extract

A long deoxyribose-nucleic-acid (DNA) molecule can be seen directly under an optical microscope if it is suitably decorated by fluorescent dyes. This makes it possible to see how a long chain responds to external forces f. The conformation of a uniformly stretched chain has been discussed by Pincus. Under a force f, acting on the two free ends, the chain configuration is modified only above a scale length ξ = kT/f where T is temperature and k is Boltzmann's constant. The chain (Figure 1a), containing N monomers, can be pictured as a string of blobs of size ξ containing g monomers with ξ = gva, where a is the monomer size (v = 1/2 in a θ solvent: the chain is ideal, v = 3/5 in a good solvent). The end-to-end distance is L = (N/g)ξ, that is,

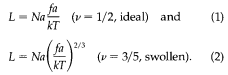
For DNA, which is a semirigid chain, ideal behavior has been observed for chain lengths up to 20 μm when f is small. At higher f ( ≅ 100 pN), Cluzel et al. found a structural phase transition, corresponding to a plateau in the curve f versus elongation. Going even further, one reaches the break point.

Another method to stretch DNA is based on optical tweezers. Here one end of the DNA is attached to a bead of glass of high polarizability, which is attracted by a region of large (optical) electric field. This was used by the Stanford group: In one series of experiments, they observed the conformations of the chain, pulled at one end by a constant force f. The friction on monomers are cumulative, and the tension along the chain is not uniform—it increases from the free end to the tethered end.

Type
Theory and Simulation of Polymers at Interfaces
Information
MRS Bulletin , Volume 22 , Issue 1 , January 1997 , pp. 48 - 52
Copyright
Copyright © Materials Research Society 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Glazer, A.N. and Ryo, H.S., Nature 359 (1992) p. 859.CrossRefGoogle Scholar
2.Pincus, P., Macromolecules 9 (1976) p. 386.CrossRefGoogle Scholar
3.Cluzel, P., Lebrun, A., Heller, C., Lavery, R., Viovy, J.L., Chatenay, D., and Caron, F., Science 271 (1996) p. 792.CrossRefGoogle Scholar
4.Bensimon, D., Simon, A., Croquette, V., and Bensimon, A., Phys. Rev. Lett. 74 (1995) p. 4754.CrossRefGoogle Scholar
5.Perkins, T.T., Smith, D.E., and Chu, S., Science 264 (1994) p. 819; T.T. Perkins, S.R. Quake, D.E. Smith, and S. Chu, Science p. 822.CrossRefGoogle Scholar
6.Brochard-Wyart, F., Europhys. Lett. 23 (1993) p. 105; F. Brochard-Wyart, Europhys. Lett. 30 (1995) p. 387.CrossRefGoogle Scholar
7.Edwards, S.F., Mol. Fluids (Gordon & Breach Science Publishers, Ithaca, NY, 1976).Google Scholar
8.de Gennes, P.G., Scaling Laws in Polymer Physics (Cornell University Press, Ithaca, NY, 1985).Google Scholar
9.Wirtz, D., Phys. Rev. Lett. 75 (12) (1995) p. 2436.CrossRefGoogle Scholar
10.de Gennes, P.G., J. Chim. Phys. 87 (1967) p. 962.Google Scholar
11.Marciano, Y. and Brochard-Wyart, F., Macromolecules 28 (1995) p. 985.CrossRefGoogle Scholar
12.Manneville, S. and Cluzel, P., private communication.Google Scholar
13.Ajdari, A., Brochard-Wyart, F., Gay, C., de Gennes, P.G., and Viovy, J.L., J. Phys. II France 5 (1995) p. 491.Google Scholar
14.Migler, K., Leger, L., and Hervet, H., Phys. Rev. Lett. 70 (3) (1993) p. 287.CrossRefGoogle Scholar
15.Brochard, F. and de Gennes, P.G., Langmuir 8 (1992) p. 3033.CrossRefGoogle Scholar