Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T20:01:52.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Defect-Mediated Rheology of Block Copolymers

Published online by Cambridge University Press:  29 November 2013

Steven D. Hudson ,
Karl R. Amundson ,
Hong G. Jeon  and
Steven D. Smith
Get access

Extract

Block copolymer melts with a near-symmetric composition can microphase-separate to form a lamellar morphology where unfavorable monomeric interactions are reduced by an antiparallel layering of the polymer chains (see Figure 2, discussed later). The symmetry of such a block copolymer is the same as for small-molecule, smectic-A liquid crystals, which also exhibit (parallel or antiparallel) layering. Because of their shared symmetry, their quasistatic mechanical properties are of the same form. To lowest order, the energy of distortion of the lamellar pattern can be expressed as a sum of a compressional/dilational and a bend energy (see, for example, Reference 2):

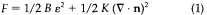
where n is a unit vector normal to the layers, and ε and ∇ n are the layer dilational and bending strain, respectively. B and K are the corresponding moduli. These have been measured only recently for block copolymers. The ratio of these moduli yields a characteristic microscopic length:

which is calculated to be a fraction of the layer spacing d0.

Similarities are also found in the dynamic properties of polymeric and smallmolecule smectics. These similarities are found at low strain rate and amplitude where the rheological response is controlled by their similar layered structures and associated defects. During either steady or dynamic shear, certain defect and domain motions are induced such that a steady-state alignment of the director has been observed. In this report, we discuss defect structure and how the much more viscous nature of these polymeric layered materials influences the distribution and relative population of each defect type. We also discuss how these defects can control material stress-relaxation behavior.

Type
Defects in Polymers
Information
MRS Bulletin , Volume 20 , Issue 9 , September 1995 , pp. 42 - 46
Copyright
Copyright © Materials Research Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davidov, D., Safinya, C.R., Kaplan, M., Dana, S.S., Schaetzing, R., Birgeneau, R.J., and Litster, J.D., Phys. Rev. B 19 (1979) p. 1,657. For example, antiparallel bilayer ordering is found in 4'-octyl-4-cyanobiphenyl (8CB) for which the extended molecular length is approximately 22 Å and the smectic layer thickness is 31.70 Å.CrossRefGoogle Scholar
2.de Gennes, P.G., The Physics of Liquid Crystals (Clarendon Press, Oxford, 1974).Google Scholar
3.Turner, M.S., Maaloum, M., Ausserre, D., Joanny, J.F., and Kunz, M., J. Phys. II France 4 (1994) p. 689.Google Scholar
4.Hudson, S.D., Lee, S.W., Amundson, K.R., and Smith, S.D., “Elastic and Dynamic Properties of Lamellar Diblock Copolymers” (unpublished manuscript).Google Scholar
5.Amundson, K. and Helfand, E., Macromolecules 26 (1993) p. 1,324.CrossRefGoogle Scholar
6.Larson, R.G., Winey, K.I., Patel, S.S., Watanabe, H., and Bruinsma, R., Rheol. Acta 32 (1993) p. 245.CrossRefGoogle Scholar
7.Safinya, C.R., Sirota, E.B., Bruinsma, R.F., Jeppesen, C., Piano, R.J., and Wenzel, L.J., Science 261 (1993) p. 588.CrossRefGoogle Scholar
8.Koppi, K.A., Tirrell, M., Bates, F.S., Almdal, K., and Colby, R.H., J. Phys. II France 2 (1992) p. 1,941.Google Scholar
9.Winey, K.I., Patel, S.S., Larson, R.G., and Watanabe, H., Macromolecules 26 (1993) p. 2,542.CrossRefGoogle Scholar
10.Winey, K.I., Patel, S.S., Larson, R.G., and Watanabe, H., Macromolecules 26 (1993) p. 4,373.CrossRefGoogle Scholar
11.Kannan, R.M. and Kornfield, J.A., Macromolecules 27 (1994) p. 1,177.CrossRefGoogle Scholar
12.Friedel, J., Dislocations (Addison-Wesley, Reading, 1964) p. 106.Google Scholar
13.Green, P., Macromolecules 28 (1995) p. 2,155.CrossRefGoogle Scholar
14.Kleman, M., Points, Lines and Walls (John Wiley & Sons, Chichester, 1983).Google Scholar
15.Bouligand, Y., in Dislocations in Solids, edited by Nabarro, F.R.N. (North-Holland, 1980) p. 299.Google Scholar
16.Allain, M. and Kléman, M., J. Phys. 48 (1987) p. 1,799.CrossRefGoogle Scholar
17.Gido, S.P., Gunther, J., Thomas, E.L., and Hoffman, D., Macromolecules 26 (1993) p. 4,506.CrossRefGoogle Scholar
18.Hull, D. and Bacon, D.J., Introduction to Dislocations (Pergamon Press, Oxford, 1984).Google Scholar
19.Herke, R.A., Clark, N.A., and Handschy, M.A., Science 267 (1995) p. 651.CrossRefGoogle Scholar
20.Hudson, S.D. and Thomas, E.L., Phys. Rev. A 44 (1991) p. 8,128.CrossRefGoogle Scholar
21.Amundson, K., Helfand, E., Quan, X., Hudson, S.D., and Smith, S.D., Macromolecules 27 (1994) p. 6,559.CrossRefGoogle Scholar
22.Helfrich, W., Appl. Phys. Lett. 17 (1970) p. 531.CrossRefGoogle Scholar
23.Delrieu, J.M., J. Chem. Phys. 60 (1974) p. 1,081.CrossRefGoogle Scholar
24.Lonberg, F., Fraden, S., Hurd, A.J., and Meyer, R.B., Phys. Rev. Lett. 52 (1984) p. 1,903.CrossRefGoogle Scholar
25.Goodby, J.W. and Pindak, R., Mol. Cryst. Liq. Cryst. 75 (1981) p. 233.CrossRefGoogle Scholar