Introduction
The generation and probing of acoustic waves of different types, such as bulk longitudinal or transverse/shear waves and surface/Rayleigh waves, are used in many well-established applications, including nondestructive testing and material characterization,Reference Levy, Bass and Stern1 signal processing,Reference Hashimoto2 dry laser cleaning,Reference Pleasants, Arnold and Kane3 chemical sensing,Reference Buvailo, Xing, Hines and Borguet4 and manipulation of fluid flow in microfluidics devices.Reference Yeo and Friend5 New opportunities that could expand the range of acoustically enabled applications are emerging from exploratory studies that report the ability of acoustic energy to drive rearrangement of crystal defects,Reference Bakai and Lazarev6,Reference Ostrovskii, Steblenko and Nadtochii7 induce crystallization in amorphous materials and thin films,Reference Ichitsubo, Matsubara, Yamamoto, Chen, Nishiyama, Saida and Anazawa8,Reference Wuenschell and Helvajian9 and affect atomic rearrangementsReference Manzo and Helvajian10,Reference Shugaev, Manzo, Wu, Zaitsev, Helvajian and Zhigilei11 and chemical reactionsReference Inoue, Matsukawa and Sato12–Reference Inoue15 on surfaces. “Traditional” application areas, such as nondestructive detection/evaluation of material heterogeneities and defects, are also experiencing a revival due to the development of new techniques that enable in situ monitoring of subsurface microstructure evolution with high temporal and spatial resolutions, as well as advanced approaches that take advantage of nonlinear acoustic effects to achieve a dramatic boost in the structural sensitivity and spatial resolution of acoustic microscopy. Many of these new developments have the potential for making a strong impact on acoustically assisted material processing and in situ/in operando material characterization.
The articles in this issue of MRS Bulletin are focused on some of the most promising and intriguing developments in the area of acoustically enabled materials synthesis, processing, and characterization, which are likely to be of interest to a broad expanse within the materials R&D communities.
Advanced methods of acoustic materials characterization
Recent improvements in the sensitivity and spatial resolution of acoustic nondestructive evaluation methods are largely achieved through utilization of nonlinear acoustic effects, as discussed in the article by ZaitsevReference Zaitsev16 in this issue. Starting from a brief overview of conventional linear acoustic diagnostic techniques (pulse-echo, resonance-based methods), the article proceeds with a broad overview of different types of nonlinear acoustic response and provides examples of the manifestation of nonlinear effects in acoustic probing of heterogeneous materials that exhibit a structure-induced “mesoscopic” acoustic nonlinearity. The applications of nonlinear acoustic probing range from characterization of nanoscale heterogeneities, such as dislocation structures, to identification of microcracks and granular materials, to macroscopic nondestructive testing of engineering structures, and to seismic studies performed at a scale of kilometers.
Among the many methods for the generation of acoustic waves, photoacoustic techniques stand out for their noncontact nature and flexibility, enabling creative design of experimental setups tuned to practical application needs. An example of a photoacoustic technique that targets in situ characterization of the evolving subsurface microstructure in samples exposed to high levels of radiation damage is provided in the article by Hofmann et al. in this issue.Reference Hofmann, Short and Dennett17 They present the laser-induced transient grating spectroscopy technique where the optical generation and probing of surface acoustic waves (SAWs) is used for analysis of microstructure evolution on the sub-microsecond time scale and with tunable depth resolution.
Materials synthesis in a cavitation bubble
While the acoustic waves in the applications discussed so far serve as the agency for nondestructive probing, a high concentration of acoustic energy can also result in material modification, damage, or even synthesis of new phases and nanomaterials. In particular, the collapse of an optically or acoustically generated bubble within a liquid can create pressure and temperature conditions that are amenable to chemical synthesis (so-called “sonochemistry”)Reference Suslick18,Reference Cintas, Cravotto, Barge and Martina19 or a significant modification of the material confined within the collapsing bubble via both chemical and physical phenomena.Reference Zhang, Gökce and Barcikowski20 The Barcikowski et al. articleReference Barcikowski, Plech, Suslick and Vogel21 in this issue brings together four experts in complementary research areas—nanoparticle synthesis by laser ablation in liquids, time-resolved probing of laser-induced phase transformations in colloidal nanoparticles, acoustic cavitation and sonochemistry, and laser-induced bubble dynamics. It provides a comprehensive and authoritative overview of the complex and multifaceted cavitation phenomenon that to a large extent controls the material synthesis in ultrasonic sonochemistry and laser ablation in liquids.
Acoustic activation of surface processes
In general, acoustic waves are not expected to directly affect atomic or molecular-level surface processes, such as diffusion, desorption, or chemical reactions. The large frequency mismatch between acoustic waves (typically ≤100 MHz) and vibrational states of surface species (on the order of THz) seemingly excludes the possibility of dynamic coupling of acoustic waves to surface processes. The periodic perturbations of the surface energy landscape associated with acoustic strain are generally small and should also have negligible effect on surface mobility or binding energy of an adsorbate. Surprisingly, however, there has been a steady growth in experimental evidence of the ability of surface and bulk acoustic waves interacting with surfaces to substantially enhance the rates and selectivity of heterogeneous catalytic reactions,Reference Inoue, Matsukawa and Sato12–Reference Inoue15 desorb molecules, atoms, and ions,Reference Denison22–Reference Ehlert, Walte and Zimmermann28 and facilitate surface diffusion of atomic clusters.Reference Manzo and Helvajian10,Reference Shugaev, Manzo, Wu, Zaitsev, Helvajian and Zhigilei11
These results are reviewed in two articles in this issue of MRS Bulletin. The article by InoueReference Inoue29 is focused on the effects of acoustic waves on chemisorption and surface reactions, which are shown to be sensitive not only to the nature of the acoustic activation (bulk versus surface waves), but also to the crystallographic surface orientation. The large magnitude of acoustic enhancement of chemical reactions, demonstrated under properly chosen experimental conditions, suggests that the acoustic stimulus can be effective in promoting heterogeneous catalysis. The article by Ma et al.Reference Ma, Zhang, Lei and Kenttämaa30 provides compelling experimental evidence of acoustically induced ejection/desorption of atoms, molecules, and particles from a thin layer of solid sample deposited on a surface of a metal foil that is irradiated from the back side by a high-energy pulsed laser beam. Possible mechanisms responsible for the ejection of molecules are discussed and the advantages of this method for “cold” desorption of heat-sensitive organic molecules in the context of mass spectrometry are demonstrated.
Mechanisms of the acoustic activation of surface processes
Despite the intriguing nature and potential practical importance of the experimental observations of the enhancement of surface catalysis, diffusion, and desorption by acoustic waves, reliable theoretical interpretation of these results is currently lacking. In the case of ejection from a continuous micrometer-thick molecular layer deposited on a metal foil, used in the laser-induced acoustic desorption setup discussed in the article by Ma et al. Reference Ma, Zhang, Lei and Kenttämaa30 in this issue, the ejection process may be driven by the direct dynamic interaction of the laser-induced stress wave with the sample layer, in a manner similar to dry laser cleaningReference Pleasants, Arnold and Kane3 or the laser-induced forward-transfer technique used for controlled material deposition.Reference Serra and Piqué31
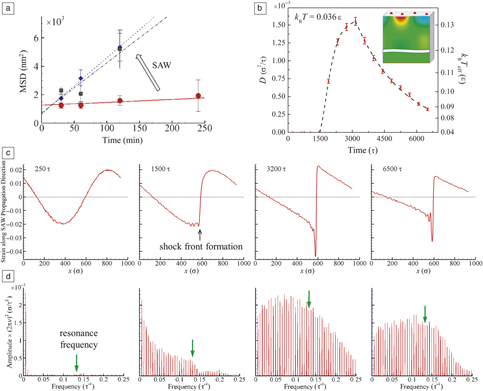
For individual atoms, molecules, and small clusters, such as the ones shown in Figure 1, however, the large frequency mismatch between the surface species and acoustic waves calls into question the contribution of the dynamic resonant coupling of the energy of an acoustic wave to surface vibrational states. The absence of an obvious explanation of the experimentally observed acoustic activation of surface processes gives rise to a range of (largely speculative) hypotheses. Some of those are based on the presumed presence of mesoscopic-scale substructures/domainsReference Kelling, Mitrelias, Matsumoto, Ostanin and King13 that can effectively couple to a long-wavelength acoustic excitation or nanoscale stressed surface features that can release the stored strain energy in response to an acoustic activation, thus providing extra energy needed for the desorption of molecules.Reference Zinovev, Veryovkin, Moore and Pellin26 Others suggest that acoustically induced variation of the spatial distribution of adsorbates may affect the surface reaction rates.Reference Reese, Hurley and Rollins14
Figure 1. Schematic representation of atomic-scale surface processes (diffusion, desorption, and chemical reactions) that can be activated by surface or bulk acoustic waves generated through optical excitation.
Modification of binding energies and diffusion barriers of adsorbed species induced by the surface strainReference Roland and Gilmer32–Reference Wu and Metiu35 has also been considered as a mechanism that may be responsible for the acoustic activation of surface processes.Reference Reese, Hurley and Rollins14 Indeed, a detailed theoretical and computational analysis performed for linear (sinusoidal) elastic SAWsReference Wu, Zaitsev and Zhigilei36 suggests that a combined effect of the transient modification of the diffusion barriers and adiabatic temperature variation due to the periodic oscillations of the acoustic strain can lead to a noticeable enhancement of adatom surface diffusion for large strain magnitudes and systems that exhibit strong strain dependence of the diffusion barriers. Moreover, theoretical analysisReference Wu, Zaitsev and Zhigilei37 suggests that structuring of surface adatoms in the presence of standing SAWs can also be achieved, thus suggesting an attractive route for acoustic control of surface self-assembly without permanent modification of the substrate. The large surface strains (∼10–2) required for reaching practically relevant levels of the diffusion enhancement and the strong quadratic scaling of the diffusion enhancement with the strain amplitude in the absence of nonlinear enrichment of the SAW spectrum by higher harmonics, however, make the assumption of the linear SAW propagation questionable and suggest that nonlinear effects should be considered.
The role of nonlinear effects
The notion of the relevance of nonlinear effects (see the article by ZaitsevReference Zaitsev16 in this issue) to the acoustic activation of surface processes is supported by a joint experimental-computational study of surface diffusion of small atomic clusters,Reference Shugaev, Manzo, Wu, Zaitsev, Helvajian and Zhigilei11 where a dramatic diffusion enhancement by SAWs was observed experimentally, as illustrated by the plots of the mean square displacement (MSD) of Au8 clusters moving on a (111) silicon substrate with and without SAWs (Figure 2). The slope of the MSD versus time dependence is proportional to the surface diffusion coefficient, and the data shown in Figure 2 demonstrate a 19-fold increase in the cluster mobility in the presence of laser-generated SAWs. The results of large-scale molecular dynamics simulationsReference Shugaev, Manzo, Wu, Zaitsev, Helvajian and Zhigilei11 clearly link the diffusion enhancement to the nonlinear sharpening of the wave profiles38 (Figure 2c), which can be described in terms of the generation of high frequency harmonics (Figure 2d) that effectively couple to the vibrational modes of the clusters (the cluster resonance frequency is marked by the green arrow in Figure 2d).
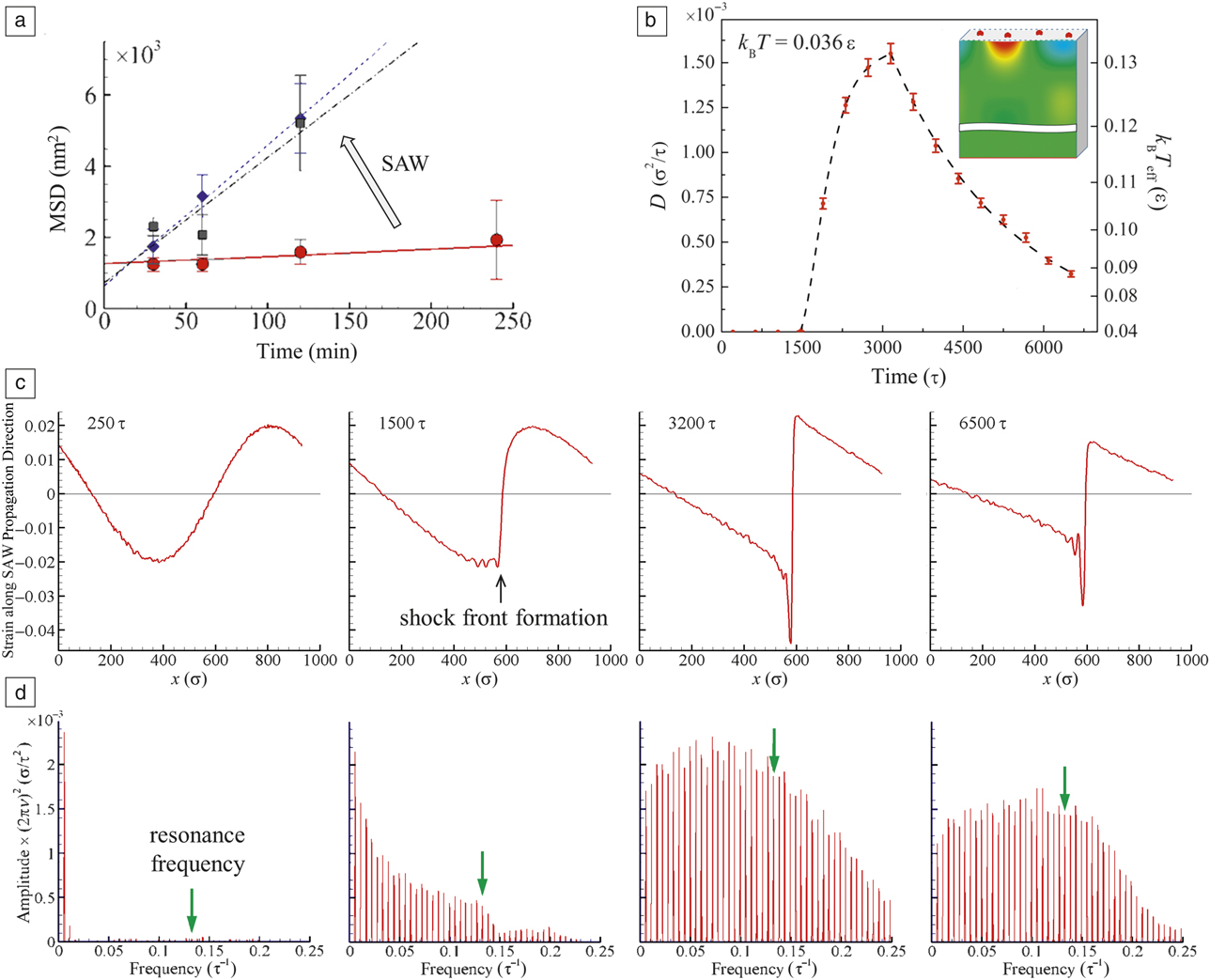
Figure 2. Acoustic activation of surface diffusion of small atomic clusters by surface acoustic waves (SAWs) (a) observed experimentally, and (b) predicted in a series of large-scale molecular dynamics simulations. The acoustic activation of surface diffusion is related to the (c) formation of a shock front and (d) generation of high-frequency harmonics capable of direct energy transfer to the clusters adsorbed on the surface. The plot in (a) shows the evolution of mean square displacement (MSD) of individual Au8 clusters moving on a (111) silicon substrate as a result of thermally activated diffusion (no SAWs, red circles) and SAW-assisted diffusion in regions located 6-mm (blue rhombus) and 12-mm (black squares) from the SAW source. The plot in (b) shows the evolution of the cluster diffusion coefficient with time of SAW propagation, with the equivalent scale of the effective temperature, T eff, which would yield the corresponding diffusion coefficients by thermal activation shown on the right side of the plot. The inset in (b) depicts a schematic representation of the computational system colored by an instantaneous pressure distribution produced by an initial sinusoidal SAW, where the color varies from red (compression) to blue (tension). (c, d) (Left to right) The temporal evolution of the SAW profile and corresponding harmonics in the wave spectrum predicted in the simulations. Lennard-Jones units are used in (b–d).Reference Shugaev, Manzo, Wu, Zaitsev, Helvajian and Zhigilei11 Note: D, diffusion coefficient; k B, the Boltzmann constant; T, temperature of the substrate; v, frequency; τ, ε unit of time; σ, energy and length parameters of Lennard–Jones potential.
Indeed, as can be seen from the changes in the cluster diffusion coefficient with time of SAW propagation (Figure 2b), the diffusion coefficient remains low initially, when the wave profile is close to a sine function. Starting from around 1500 τ (τ is a unit of time used in the simulationReference Shugaev, Manzo, Wu, Zaitsev, Helvajian and Zhigilei11), however, the diffusion coefficient rapidly increases and reaches a maximum value that is more than 4500× higher than the value of thermal diffusion at the temperature of the substrate. This enhancement of surface diffusion corresponds to an equivalent increase of the substrate temperature by a factor of about 3.7. The plots of the wave profiles shown in Figure 2c demonstrate that the large mobility enhancement coincides with sharpening of the SAW profile and generation of a shock front. During the subsequent propagation of the SAW, the wave amplitude and the shock front sharpness decrease due to the strong dissipation near the wave front, as the high-frequency harmonics associated with the shock formation efficiently couple with thermal phonons. Nevertheless, despite a substantial attenuation of the wave by the time of 6500 τ, and the corresponding decrease of the cluster mobility, the diffusion coefficient remains almost 1000× higher than that of the thermally activated diffusion. The direct correlation between the evolution of the high frequency components of the wave spectrum and the diffusion enhancement suggests that the latter can be attributed to the dynamic coupling of high-frequency harmonics with the cluster vibrational modes that facilitates an effective transfer of the acoustic energy to the cluster motion.
The interactions of a nonlinear wave with surface adsorbates, atomistic/mesoscopic heterogeneities, and defects are likely to strongly affect the evolution of the wave itself, thus resulting in a mutual feedback between the acoustic activation of surface processes and the frequency-dependent dissipation/generation of the wave harmonics. In general, the results of the simulations and experiments suggest that the nonlinear sharpening of the acoustic waves may play an important role in the activation of atomic-scale surface processes, and the nonlinear effects should be considered, along with other mechanisms discussed in articles by InoueReference Inoue29 and Ma et al.Reference Ma, Zhang, Lei and Kenttämaa30 in this issue, in the interpretation of the highly intriguing, but not yet fully understood experimental evidence of the acoustic enhancement of surface processes.
Concluding remarks
The diversity of the physical and chemical processes that can be activated or enhanced by an acoustic stimulus, as well as a wide range of current and emerging applications already utilizing acoustic waves for materials characterization, synthesis, and modification, discussed in the articles in this issue of MRS Bulletin, suggest that the delivery and manipulation of acoustic energy is likely to play an increasingly important role in materials science and engineering. Progress in the incorporation of the acoustic methods into mainstream materials synthesis and processing techniques requires significant advancement in the fundamental understanding of the interaction of acoustic waves with different elements of the material microstructure, particularly in the nonlinear regime, as well as the mechanisms of acoustically induced structural and phase transformations. This progress can only be achieved through stronger interdisciplinary interactions between the materials research community and researchers working in areas as disparate as nonlinear acoustics, cavitation and bubble dynamics, seismology, ultrasonic imaging, and surface chemistry.
Acknowledgments
L.V. Z. acknowledges financial support from the National Science Foundation through Grant No. CMMI-1562929.

Leonid V. Zhigilei is a professor of materials science and engineering at the University of Virginia. He studied materials science at Leningrad Polytechnic Institute and earned his PhD degree at Tomsk State University and St. Petersburg State University, Russia. Before joining the faculty of the University of Virginia, he was a postdoctoral researcher in the Department of Chemistry at The Pennsylvania State University. His research interests include multiscale modeling of materials behavior far from equilibrium, mechanisms of phase transformations, nanomaterials, and surface processes. Zhigilei can be reached by email at [email protected].

Henry Helvajian is a senior scientist at The Aerospace Corporation. He received his BS and MS degrees at Stanford University concentrating on lasers and quantum electronics, and earned his PhD degree at the University of Southern California in photochemistry and gas-phase kinetics/spectroscopy. He was a NAS/NRC postdoctoral researcher in the Chemistry Division at the Naval Research Laboratories prior to joining The Aerospace Corporation. His research interests include laser fabrication of glass-ceramic microelectromechanical systems, manufacturing processes for mass-producing nanosatellites, laser ultrasonic processes in materials synthesis, altering speed of sound by lasers, and process control for additive manufacturing. Helvajian can be reached by email at [email protected].