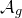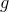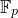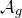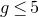1. Introduction
Arithmetic properties of abelian varieties are strongly linked to the geometry of their moduli spaces. Here we study both the birational geometry over
![]() $\mathbb{Q}$
of the coarse moduli space
$\mathbb{Q}$
of the coarse moduli space
![]() ${\mathcal{A}}_g$
of principally polarised abelian varieties (ppavs), and lifting and other arithmetic properties of ppavs themselves.
${\mathcal{A}}_g$
of principally polarised abelian varieties (ppavs), and lifting and other arithmetic properties of ppavs themselves.
1.1 Lifting abelian varieties
For any prime
![]() $p$
and any elliptic curve
$p$
and any elliptic curve
![]() $E_p$
over
$E_p$
over
![]() ${\mathbb{F}}_p$
, there exists an elliptic curve
${\mathbb{F}}_p$
, there exists an elliptic curve
![]() $E$
over
$E$
over
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
![]() $E_p$
is the reduction modulo
$E_p$
is the reduction modulo
![]() $p$
of
$p$
of
![]() $E$
(we say that
$E$
(we say that
![]() $E$
is a lift of
$E$
is a lift of
![]() $E_p$
to
$E_p$
to
![]() $\mathbb{Q}$
). Indeed, one simply takes a suitable lift of the coefficients of
$\mathbb{Q}$
). Indeed, one simply takes a suitable lift of the coefficients of
![]() $E_p$
.
$E_p$
.
For higher-dimensional abelian varieties the problem becomes more interesting. Firstly, we at least need that the abelian variety
![]() $A_p$
lifts from
$A_p$
lifts from
![]() ${\mathbb{F}}_p$
to
${\mathbb{F}}_p$
to
![]() ${\mathbb{Q}}_p$
; to guarantee this we assume that
${\mathbb{Q}}_p$
; to guarantee this we assume that
![]() $A_p$
is equipped with a principal polarisation [Reference OortOor71, Corollary 2.4.2]. It is not too difficult to see that principally polarised abelian surfaces always lift to
$A_p$
is equipped with a principal polarisation [Reference OortOor71, Corollary 2.4.2]. It is not too difficult to see that principally polarised abelian surfaces always lift to
![]() $\mathbb{Q}$
as the generic such surface is the Jacobian of a hyperelliptic curve (see Section 4.3). One of our first results is that lifting can be achieved in dimension 3, and moreover for finitely many primes simultaneously.
$\mathbb{Q}$
as the generic such surface is the Jacobian of a hyperelliptic curve (see Section 4.3). One of our first results is that lifting can be achieved in dimension 3, and moreover for finitely many primes simultaneously.
For an abelian variety
![]() $A$
over
$A$
over
![]() $\mathbb{Q}$
and a prime
$\mathbb{Q}$
and a prime
![]() $p$
, we denote by
$p$
, we denote by
![]() $A_{{\mathbb{F}}_p}$
the reduction modulo
$A_{{\mathbb{F}}_p}$
the reduction modulo
![]() $p$
of the Néron model of
$p$
of the Néron model of
![]() $A$
.
$A$
.
Theorem 1.1.
Let
![]() $S$
be a finite set of rational primes, and for each
$S$
be a finite set of rational primes, and for each
![]() $p \in S$
fix
$p \in S$
fix
![]() $A_p$
, a principally polarised abelian
$A_p$
, a principally polarised abelian
![]() $3$
-fold over
$3$
-fold over
![]() ${\mathbb{F}}_p$
. Then there exists a principally polarised abelian
${\mathbb{F}}_p$
. Then there exists a principally polarised abelian
![]() $3$
-fold
$3$
-fold
![]() $A$
over
$A$
over
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
![]() $A_p \cong A_{{\mathbb{F}}_p} {\rm \ for\ all\ }p \in S$
as ppavs.
$A_p \cong A_{{\mathbb{F}}_p} {\rm \ for\ all\ }p \in S$
as ppavs.
This property should not hold in higher dimension.
Theorem 1.2.
Let
![]() $g \geq 7$
and assume the Bombieri–Lang conjecture. Then, for all but finitely many primes
$g \geq 7$
and assume the Bombieri–Lang conjecture. Then, for all but finitely many primes
![]() $p$
, there exists a principally polarised abelian
$p$
, there exists a principally polarised abelian
![]() $g$
-fold
$g$
-fold
![]() $A_p$
over
$A_p$
over
![]() ${\mathbb{F}}_p$
such that
${\mathbb{F}}_p$
such that
![]() $A_p \not \cong A_{{\mathbb{F}}_p}$
for any principally polarised abelian
$A_p \not \cong A_{{\mathbb{F}}_p}$
for any principally polarised abelian
![]() $g$
-folds
$g$
-folds
![]() $A$
over
$A$
over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
1.2 Rationality properties of moduli spaces
We achieve our arithmetic results through consideration of the birational geometry of the coarse moduli space
![]() ${\mathcal{A}}_g$
of principally polarised abelian
${\mathcal{A}}_g$
of principally polarised abelian
![]() $g$
-folds over
$g$
-folds over
![]() $\mathbb{Q}$
. This has been much studied over the complex numbers. It is known that
$\mathbb{Q}$
. This has been much studied over the complex numbers. It is known that
![]() ${\mathcal{A}}_g$
is unirational over
${\mathcal{A}}_g$
is unirational over
![]() $\mathbb{C}$
for
$\mathbb{C}$
for
![]() $g\le 5$
, and rational over
$g\le 5$
, and rational over
![]() $\mathbb{C}$
for
$\mathbb{C}$
for
![]() $g\le{3}$
. On the other hand, if
$g\le{3}$
. On the other hand, if
![]() $g\ge 7$
then
$g\ge 7$
then
![]() ${\mathcal{A}}_g$
is of general type [Reference TaiTai82], and
${\mathcal{A}}_g$
is of general type [Reference TaiTai82], and
![]() ${\mathcal{A}}_6$
has non-negative Kodaira dimension [Reference Dittmann, Manni and ScheithauerDMS21]. Questions about the rationality of
${\mathcal{A}}_6$
has non-negative Kodaira dimension [Reference Dittmann, Manni and ScheithauerDMS21]. Questions about the rationality of
![]() ${\mathcal{A}}_g$
over non-closed fields seem by contrast to have had little attention, and we address some of them here, over
${\mathcal{A}}_g$
over non-closed fields seem by contrast to have had little attention, and we address some of them here, over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
We first consider unirationality and, incorporating previous results, obtain the following theorem.
Theorem 1.3.
The coarse moduli space
![]() ${\mathcal{A}}_g$
of ppavs is unirational over
${\mathcal{A}}_g$
of ppavs is unirational over
![]() $\mathbb{Q}$
if and only if
$\mathbb{Q}$
if and only if
![]() $g\le 5$
.
$g\le 5$
.
This result has motivation from the recent paper [Reference Masser and ZannierMZ20], in which Masser and Zannier prove various results on the existence of abelian varieties over
![]() $\overline{{\mathbb{Q}}}$
that are not isogenous to Jacobians. Some of their results also hold for abelian varieties over
$\overline{{\mathbb{Q}}}$
that are not isogenous to Jacobians. Some of their results also hold for abelian varieties over
![]() $\mathbb{Q}$
, but for
$\mathbb{Q}$
, but for
![]() $g=4$
and
$g=4$
and
![]() $g=5$
that refinement is conditional on the unirationality of
$g=5$
that refinement is conditional on the unirationality of
![]() ${\mathcal{A}}_g$
over
${\mathcal{A}}_g$
over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
From this and [Reference Masser and ZannierMZ20, Theorem 1.5, Corollary 1.6] we obtain the following immediate application, which is new for
![]() $g=4,\,5$
(see [Reference Masser and ZannierMZ20, Theorem 1.5] for a stronger statement).
$g=4,\,5$
(see [Reference Masser and ZannierMZ20, Theorem 1.5] for a stronger statement).
Corollary 1.4.
Let
![]() $k$
be a number field. For
$k$
be a number field. For
![]() $g=\,4,\,5$
, there exists a principally polarised abelian
$g=\,4,\,5$
, there exists a principally polarised abelian
![]() $g$
-fold over
$g$
-fold over
![]() $k$
that is Hodge generic and not isogenous to any Jacobian.
$k$
that is Hodge generic and not isogenous to any Jacobian.
We prove Theorem1.3 by showing that the Prym moduli space
![]() ${\mathcal{R}}_{g+1}$
is unirational for
${\mathcal{R}}_{g+1}$
is unirational for
![]() $g=4,\,5$
. This is sufficient to get unirationality of
$g=4,\,5$
. This is sufficient to get unirationality of
![]() ${\mathcal{A}}_g$
, as the Prym map
${\mathcal{A}}_g$
, as the Prym map
![]() ${\mathcal{R}}_{g+1} \to{\mathcal{A}}_g$
is dominant for
${\mathcal{R}}_{g+1} \to{\mathcal{A}}_g$
is dominant for
![]() $g \leq 5$
over any field of characteristic not equal to
$g \leq 5$
over any field of characteristic not equal to
![]() $2$
[Reference BeauvilleBea77, Theorem 6.5].
$2$
[Reference BeauvilleBea77, Theorem 6.5].
For deeper rationality properties, it is known that
![]() ${\mathcal{A}}_2$
is rational over any field, by work of Igusa [Reference IgusaIgu60]. The rationality of
${\mathcal{A}}_2$
is rational over any field, by work of Igusa [Reference IgusaIgu60]. The rationality of
![]() ${\mathcal{A}}_3$
over
${\mathcal{A}}_3$
over
![]() $\mathbb{C}$
was first proven by Katsylo [Reference KatsyloKat96] (see also Böhning’s exposition [Reference BöhningBöh10]). It seems possible that this result could also hold over
$\mathbb{C}$
was first proven by Katsylo [Reference KatsyloKat96] (see also Böhning’s exposition [Reference BöhningBöh10]). It seems possible that this result could also hold over
![]() $\mathbb{Q}$
; however, Katsylo’s proof is notoriously delicate and technical. We content ourselves with the following weaker statement, which has a much simpler proof and is sufficient for arithmetic applications.
$\mathbb{Q}$
; however, Katsylo’s proof is notoriously delicate and technical. We content ourselves with the following weaker statement, which has a much simpler proof and is sufficient for arithmetic applications.
Theorem 1.5.
The coarse moduli space
![]() ${\mathcal{A}}_3$
is stably rational over
${\mathcal{A}}_3$
is stably rational over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
1.3 Weak approximation for algebraic stacks
Theorem1.5 is the key geometric input for the proof of Theorem1.1. Namely, one can interpret Theorem1.1 as a version of weak approximation for the moduli stack
![]() $\mathscr{A}_3$
of principally polarised abelian 3-folds. Recall that a smooth variety
$\mathscr{A}_3$
of principally polarised abelian 3-folds. Recall that a smooth variety
![]() $X$
over a number field
$X$
over a number field
![]() $k$
is said to satisfy weak approximation if
$k$
is said to satisfy weak approximation if
![]() $X(k)$
is dense in
$X(k)$
is dense in
![]() $\prod _v X(k_v)$
, where the product is over all places
$\prod _v X(k_v)$
, where the product is over all places
![]() $v$
of
$v$
of
![]() $k$
. We prove a version of this for the stack
$k$
. We prove a version of this for the stack
![]() $\mathscr{A}_3$
(see Section 4 for definitions for stacks).
$\mathscr{A}_3$
(see Section 4 for definitions for stacks).
Theorem 1.6.
The stack
![]() $\mathscr{A}_3$
satisfies weak approximation over any number field
$\mathscr{A}_3$
satisfies weak approximation over any number field
![]() $k$
.
$k$
.
The classical weak approximation theorem implies that rational varieties satisfy weak approximation, and a fibration argument extends this to stably rational varieties. However, Theorem1.5 does not immediately imply Theorem1.6; indeed, there are algebraic stacks that fail weak approximation but whose coarse moduli space satisfies weak approximation (see Example 4.8). To exclude this possibility for
![]() $\mathscr{A}_3$
one needs to be careful with twists. Theorem1.1 is then an application of this weak approximation result.
$\mathscr{A}_3$
one needs to be careful with twists. Theorem1.1 is then an application of this weak approximation result.
1.4 Questions
Our results raise the following question, to which we do not know the answer.
Question 1.7. Do
![]() ${\mathcal{A}}_4$
and
${\mathcal{A}}_4$
and
![]() ${\mathcal{A}}_5$
satisfy weak weak approximation (i.e., weak approximation away from a finite set of places)?
${\mathcal{A}}_5$
satisfy weak weak approximation (i.e., weak approximation away from a finite set of places)?
Standard conjectures in arithmetic geometry, together with the unirationality from Theorem1.3, would imply a positive answer to Question 1.7. This in turn would give a version of Theorem1.6 for
![]() $\mathscr{A}_5$
, and a version of Theorem1.1 for
$\mathscr{A}_5$
, and a version of Theorem1.1 for
![]() $g=5$
away from finitely many primes. The case of
$g=5$
away from finitely many primes. The case of
![]() $\mathscr{A}_4$
is less clear as here the generic gerbe is non-neutral (see Lemma 4.11).
$\mathscr{A}_4$
is less clear as here the generic gerbe is non-neutral (see Lemma 4.11).
Question 1.8. Can one prove an unconditional version of Theorem 1.2?
1.5 Conventions
We denote by
![]() $\mathscr{A}_g$
the moduli stack of principally polarised abelian
$\mathscr{A}_g$
the moduli stack of principally polarised abelian
![]() $g$
-folds over
$g$
-folds over
![]() $\mathbb{Z}$
and by
$\mathbb{Z}$
and by
![]() ${\mathcal{A}}_g$
its coarse moduli space. The stack
${\mathcal{A}}_g$
its coarse moduli space. The stack
![]() $\mathscr{A}_g$
is smooth over
$\mathscr{A}_g$
is smooth over
![]() $\mathbb{Z}$
[Reference OortOor71, Theorem 2.4.1]. We sometimes abuse notation and also denote by
$\mathbb{Z}$
[Reference OortOor71, Theorem 2.4.1]. We sometimes abuse notation and also denote by
![]() $\mathscr{A}_g$
the base change of the stack to some field, which will be clear from the context.
$\mathscr{A}_g$
the base change of the stack to some field, which will be clear from the context.
For a group scheme
![]() $G$
we denote by
$G$
we denote by
![]() $BG$
the associated classifying stack. Regarding gerbes, we use the conventions of [Reference OlssonOls16, Chapter 12]. If
$BG$
the associated classifying stack. Regarding gerbes, we use the conventions of [Reference OlssonOls16, Chapter 12]. If
![]() $G$
is an abelian group scheme, we say that a
$G$
is an abelian group scheme, we say that a
![]() $G$
-gerbe is neutral if it has a section; this is equivalent to being isomorphic to
$G$
-gerbe is neutral if it has a section; this is equivalent to being isomorphic to
![]() $BG$
.
$BG$
.
For an algebraic stack
![]() $\mathscr{X}$
and a scheme
$\mathscr{X}$
and a scheme
![]() $S$
, we abuse notation and denote by
$S$
, we abuse notation and denote by
![]() $\mathscr{X}(S)$
the set of isomorphism classes of
$\mathscr{X}(S)$
the set of isomorphism classes of
![]() $S$
-points of
$S$
-points of
![]() $\mathscr{X}$
(rather than the groupoid).
$\mathscr{X}$
(rather than the groupoid).
2. Background on moduli
In this section we outline the known results over the complex numbers and make some remarks about certain moduli spaces associated with curves, which we shall use as auxiliaries.
Let
![]() $k$
be a field. Recall that a variety
$k$
be a field. Recall that a variety
![]() $X$
over
$X$
over
![]() $k$
is said to be rational (respectively, unirational) if it admits a birational (respectively, dominant rational) map from a projective space. It is said to be stably rational if
$k$
is said to be rational (respectively, unirational) if it admits a birational (respectively, dominant rational) map from a projective space. It is said to be stably rational if
![]() $X \times{\mathbb{P}}^n$
is rational for some
$X \times{\mathbb{P}}^n$
is rational for some
![]() $n$
.
$n$
.
2.1 Known rationality results
The coarse moduli spaces
![]() ${\mathcal{A}}_g$
have been much studied over the complex numbers from a birational point of view. With the exception of the case (
${\mathcal{A}}_g$
have been much studied over the complex numbers from a birational point of view. With the exception of the case (
![]() $g=6$
), the broad picture remains as described in [Reference Hulek and SankaranHS02], to which we refer for more details.
$g=6$
), the broad picture remains as described in [Reference Hulek and SankaranHS02], to which we refer for more details.
2.1.1
 $(g=2)$
$(g=2)$
Igusa [Reference IgusaIgu60, Theorem 5] showed that
![]() ${\mathcal{A}}_2 = \mathcal{M}_2$
is rational over any field, and there are numerous results on the moduli space for abelian surfaces with non-principal polarisations or level structures.
${\mathcal{A}}_2 = \mathcal{M}_2$
is rational over any field, and there are numerous results on the moduli space for abelian surfaces with non-principal polarisations or level structures.
2.1.2
 $(g=3)$
$(g=3)$
It is easy to see that
![]() ${\mathcal{A}}_3$
is unirational over
${\mathcal{A}}_3$
is unirational over
![]() $\mathbb{C}$
. Katsylo [Reference KatsyloKat96] showed that
$\mathbb{C}$
. Katsylo [Reference KatsyloKat96] showed that
![]() $\mathcal{M}_3$
(and hence
$\mathcal{M}_3$
(and hence
![]() ${\mathcal{A}}_3$
, by Torelli) is rational over
${\mathcal{A}}_3$
, by Torelli) is rational over
![]() $\mathbb{C}$
; we discuss this in Section 2.2 below.
$\mathbb{C}$
; we discuss this in Section 2.2 below.
2.1.3
 $(g=4)$
$(g=4)$
The first proof that
![]() ${\mathcal{A}}_4$
is unirational over
${\mathcal{A}}_4$
is unirational over
![]() $\mathbb{C}$
was given by Clemens [Reference ClemensCle83], using intermediate Jacobians. Other proofs were subsequently given by Verra [Reference VerraVer08] and by Izadi, Lo Giudice and the second author [Reference Izadi, Lo Giudice and SankaranILS09]. Of these, the proof in [Reference Izadi, Lo Giudice and SankaranILS09], which uses the moduli space of Prym curves (see Section 2.3 below), seems the easiest to adapt to non-closed fields.
$\mathbb{C}$
was given by Clemens [Reference ClemensCle83], using intermediate Jacobians. Other proofs were subsequently given by Verra [Reference VerraVer08] and by Izadi, Lo Giudice and the second author [Reference Izadi, Lo Giudice and SankaranILS09]. Of these, the proof in [Reference Izadi, Lo Giudice and SankaranILS09], which uses the moduli space of Prym curves (see Section 2.3 below), seems the easiest to adapt to non-closed fields.
2.1.4
 $(g=5)$
$(g=5)$
The first proofs that
![]() ${\mathcal{A}}_5$
is unirational over
${\mathcal{A}}_5$
is unirational over
![]() $\mathbb{C}$
were given by Donagi [Reference DonagiDon84] and by Mori and Mukai [Reference Mori and MukaiMM83]. There is a different proof in [Reference VerraVer84] and a more recent one by Farkas and Verra [Reference Farkas and VerraFV16]. All of these use Prym curves. We found the argument in [Reference Farkas and VerraFV16] the easiest to adapt for our purposes.
$\mathbb{C}$
were given by Donagi [Reference DonagiDon84] and by Mori and Mukai [Reference Mori and MukaiMM83]. There is a different proof in [Reference VerraVer84] and a more recent one by Farkas and Verra [Reference Farkas and VerraFV16]. All of these use Prym curves. We found the argument in [Reference Farkas and VerraFV16] the easiest to adapt for our purposes.
2.1.5
 $(g\ge 6)$
$(g\ge 6)$
The spaces
![]() ${\mathcal{A}}_g$
are non-rational for
${\mathcal{A}}_g$
are non-rational for
![]() $g\gt 5$
, at least in characteristic 0. Tai [Reference TaiTai82], building on earlier work of Mumford and of Freitag, showed that
$g\gt 5$
, at least in characteristic 0. Tai [Reference TaiTai82], building on earlier work of Mumford and of Freitag, showed that
![]() ${\mathcal{A}}_g$
is of general type for
${\mathcal{A}}_g$
is of general type for
![]() $g\ge 7$
. The case of
$g\ge 7$
. The case of
![]() ${\mathcal{A}}_6$
remained completely mysterious until 2020, when Dittman, Salvati Manni, and Scheithauer [Reference Dittmann, Manni and ScheithauerDMS21] showed that the second plurigenus is positive: thus the Kodaira dimension is non-negative.
${\mathcal{A}}_6$
remained completely mysterious until 2020, when Dittman, Salvati Manni, and Scheithauer [Reference Dittmann, Manni and ScheithauerDMS21] showed that the second plurigenus is positive: thus the Kodaira dimension is non-negative.
2.2 Moduli of curves
In view of Katsylo’s result, it is natural to ask whether
![]() ${\mathcal{A}}_3$
is rational over
${\mathcal{A}}_3$
is rational over
![]() $\mathbb{Q}$
. What Katsylo proves directly, however, is that
$\mathbb{Q}$
. What Katsylo proves directly, however, is that
![]() $\mathcal{M}_3$
is rational (over
$\mathcal{M}_3$
is rational (over
![]() $\mathbb{C}$
), and the wider context into which the proof naturally fits is the moduli of curves rather than of abelian varieties. Katsylo’s proof is one of many rationality proofs for moduli spaces of curves: for some examples, see [Reference Verra, Farkas and MorrisonVer13]. The main tool for many of these is classical invariant theory. Few of them are written with much attention to fields of definition. Shepherd-Barron’s proof [Reference Shepherd-BarronS-B89] that
$\mathbb{C}$
), and the wider context into which the proof naturally fits is the moduli of curves rather than of abelian varieties. Katsylo’s proof is one of many rationality proofs for moduli spaces of curves: for some examples, see [Reference Verra, Farkas and MorrisonVer13]. The main tool for many of these is classical invariant theory. Few of them are written with much attention to fields of definition. Shepherd-Barron’s proof [Reference Shepherd-BarronS-B89] that
![]() $\mathcal{M}_6$
is rational over
$\mathcal{M}_6$
is rational over
![]() $\mathbb{Q}$
is an exception. In fact, Katsylo’s proof for
$\mathbb{Q}$
is an exception. In fact, Katsylo’s proof for
![]() $\mathcal{M}_3$
is among the most complicated of these arguments.
$\mathcal{M}_3$
is among the most complicated of these arguments.
2.3 Prym curves
A Prym curve (of genus
![]() $g$
) over a scheme
$g$
) over a scheme
![]() $S$
is a pair
$S$
is a pair
![]() $(D,C)$
where
$(D,C)$
where
![]() $C$
is a smooth proper scheme over
$C$
is a smooth proper scheme over
![]() $S$
whose fibres are smooth projective geometrically integral curves of genus
$S$
whose fibres are smooth projective geometrically integral curves of genus
![]() $g$
, and
$g$
, and
![]() $D \to C$
is a finite étale morphism of degree
$D \to C$
is a finite étale morphism of degree
![]() $2$
whose fibres over
$2$
whose fibres over
![]() $S$
are geometrically integral. We denote by
$S$
are geometrically integral. We denote by
![]() $\mathscr{R}_g$
the moduli stack of Prym curves of genus
$\mathscr{R}_g$
the moduli stack of Prym curves of genus
![]() $g$
and by
$g$
and by
![]() ${\mathcal{R}}_g$
its coarse moduli space.
${\mathcal{R}}_g$
its coarse moduli space.
An explicit construction of this stack over
![]() ${\mathbb{Z}}[1/2]$
can be found in the proof of [Reference BeauvilleBea77, Theorem 6.5], which also constructs a morphism (the Prym map)
${\mathbb{Z}}[1/2]$
can be found in the proof of [Reference BeauvilleBea77, Theorem 6.5], which also constructs a morphism (the Prym map)
![]() $\mathscr{R}_g \to \mathscr{A}_{g-1}$
of stacks over
$\mathscr{R}_g \to \mathscr{A}_{g-1}$
of stacks over
![]() ${\mathbb{Z}}[1/2]$
. Moreover,
${\mathbb{Z}}[1/2]$
. Moreover,
![]() $\mathscr{R}_g \to \mathscr{A}_{g-1}$
is dominant for
$\mathscr{R}_g \to \mathscr{A}_{g-1}$
is dominant for
![]() $g \leq 6$
, by [Reference BeauvilleBea77, Lemma 6.5.2].
$g \leq 6$
, by [Reference BeauvilleBea77, Lemma 6.5.2].
3. Rationality results
3.1 Stable rationality of moduli of hypersurfaces
We will prove that
![]() ${\mathcal{A}}_3$
is stably rational by showing that the moduli space of plane quartic curves is stably rational. Our argument is sufficiently robust that it also works for other moduli of hypersurfaces. Our result is as follows.
${\mathcal{A}}_3$
is stably rational by showing that the moduli space of plane quartic curves is stably rational. Our argument is sufficiently robust that it also works for other moduli of hypersurfaces. Our result is as follows.
Theorem 3.1.
Let
![]() $d,n \geq 2$
with
$d,n \geq 2$
with
![]() $(d,n) \neq (3,2)$
. Let
$(d,n) \neq (3,2)$
. Let
![]() $k$
be a field and
$k$
be a field and
![]() $\mathcal{H}_{d,n}$
denote the Hilbert scheme of hypersurfaces of degree
$\mathcal{H}_{d,n}$
denote the Hilbert scheme of hypersurfaces of degree
![]() $d$
in
$d$
in
![]() ${\mathbb{P}}^n$
. The group
${\mathbb{P}}^n$
. The group
![]() ${\rm PGL}_{n+1}$
acts on
${\rm PGL}_{n+1}$
acts on
![]() $\mathcal{H}_{d,n}$
in a natural way via linear change of variables. Assume that
$\mathcal{H}_{d,n}$
in a natural way via linear change of variables. Assume that
![]() ${\rm char}(k)$
does not divide
${\rm char}(k)$
does not divide
![]() $n+1$
and that
$n+1$
and that
![]() $\gcd (d,n+1)=1$
. Then
$\gcd (d,n+1)=1$
. Then
![]() $\mathcal{H}_{d,n}/{\rm PGL}_{n+1}$
is stably rational.
$\mathcal{H}_{d,n}/{\rm PGL}_{n+1}$
is stably rational.
Proof.
The case
![]() $d = 2$
is classical so we assume
$d = 2$
is classical so we assume
![]() $d \gt 2$
. Let
$d \gt 2$
. Let
![]() $V_{d,n}={{\rm H}}^0({\mathbb{P}}^n,{\mathcal{O}}_{{\mathbb{P}}^n}(d))$
be the vector space of forms of degree
$V_{d,n}={{\rm H}}^0({\mathbb{P}}^n,{\mathcal{O}}_{{\mathbb{P}}^n}(d))$
be the vector space of forms of degree
![]() $d$
in
$d$
in
![]() $(n+1)$
variables. The group
$(n+1)$
variables. The group
![]() ${\rm SL}_{n+1}$
acts on
${\rm SL}_{n+1}$
acts on
![]() $V_{d,n}$
in a natural way via linear change of variables. The coprimality conditions ensure that the central copy of
$V_{d,n}$
in a natural way via linear change of variables. The coprimality conditions ensure that the central copy of
![]() $\mu _{n+1} \subset {\rm SL}_{n+1}$
acts faithfully on
$\mu _{n+1} \subset {\rm SL}_{n+1}$
acts faithfully on
![]() $V_{d,n}$
. Moreover, the induced action of
$V_{d,n}$
. Moreover, the induced action of
![]() ${\rm SL}_{n+1}$
on
${\rm SL}_{n+1}$
on
![]() $\mathcal{H}_{d,n}$
factors through the
$\mathcal{H}_{d,n}$
factors through the
![]() ${\rm SL}_{n+1}/\mu _{n+1}={\rm PGL}_{n+1}$
-action. We obtain the following commutative diagram.
${\rm SL}_{n+1}/\mu _{n+1}={\rm PGL}_{n+1}$
-action. We obtain the following commutative diagram.

The action of
![]() ${\rm SL}_{n+1}$
on
${\rm SL}_{n+1}$
on
![]() $V_{d,n}$
is generically free: indeed,
$V_{d,n}$
is generically free: indeed,
![]() $\mu _{n+1}$
acts faithfully and the action of
$\mu _{n+1}$
acts faithfully and the action of
![]() ${\rm PGL}_{n+1}$
on
${\rm PGL}_{n+1}$
on
![]() $\mathcal{H}_{d,n}$
is generically free as there exist hypersurfaces of degree
$\mathcal{H}_{d,n}$
is generically free as there exist hypersurfaces of degree
![]() $d$
with trivial linear automorphism group [Reference PoonenPoo05]. We conclude that the generic fibre of the left-hand map is an
$d$
with trivial linear automorphism group [Reference PoonenPoo05]. We conclude that the generic fibre of the left-hand map is an
![]() ${\rm SL}_{n+1}$
-torsor. But such a torsor is necessary trivial as
${\rm SL}_{n+1}$
-torsor. But such a torsor is necessary trivial as
![]() ${{\rm H}}^1(k,{\rm SL}_{n+1}) = 0$
for any field
${{\rm H}}^1(k,{\rm SL}_{n+1}) = 0$
for any field
![]() $k$
[Reference Platonov and RapinchukPR94, Lemma 2.3]. We conclude that
$k$
[Reference Platonov and RapinchukPR94, Lemma 2.3]. We conclude that
![]() $V_{d,n}$
is birational to
$V_{d,n}$
is birational to
![]() ${\rm SL}_{n+1} \times (V_{d,n} /{\rm SL}_{n+1})$
.
${\rm SL}_{n+1} \times (V_{d,n} /{\rm SL}_{n+1})$
.
However,
![]() ${\rm SL}_{n+1}$
is rational over
${\rm SL}_{n+1}$
is rational over
![]() $k$
. This can be seen by noting that the determinant is linear in the coordinate
$k$
. This can be seen by noting that the determinant is linear in the coordinate
![]() $x_{1,1}$
, and thus one can solve for
$x_{1,1}$
, and thus one can solve for
![]() $x_{1,1}$
. Thus
$x_{1,1}$
. Thus
![]() $V_{d,n} /{\rm SL}_{n+1}$
is stably rational.
$V_{d,n} /{\rm SL}_{n+1}$
is stably rational.
Next, the top arrow in the diagram is a
![]() ${\mathbb{G}}_{{\rm m}}$
-torsor. The bottom arrow is thus a
${\mathbb{G}}_{{\rm m}}$
-torsor. The bottom arrow is thus a
![]() ${\mathbb{G}}_{{\rm m}}/\mu _{n+1} ={\mathbb{G}}_{{\rm m}}$
-torsor (here the map
${\mathbb{G}}_{{\rm m}}/\mu _{n+1} ={\mathbb{G}}_{{\rm m}}$
-torsor (here the map
![]() $\mu _{n+1} \to{\mathbb{G}}_{{\rm m}}$
is the one induced by the
$\mu _{n+1} \to{\mathbb{G}}_{{\rm m}}$
is the one induced by the
![]() ${\rm SL}_{n+1}$
-action and not necessarily the standard embedding). By Hilbert’s Theorem 90 the generic fibre is the trivial torsor: thus we see that
${\rm SL}_{n+1}$
-action and not necessarily the standard embedding). By Hilbert’s Theorem 90 the generic fibre is the trivial torsor: thus we see that
![]() $\mathcal{H}_{d,n}/{\rm PGL}_{n+1}$
is stably birational to
$\mathcal{H}_{d,n}/{\rm PGL}_{n+1}$
is stably birational to
![]() $V_{d,n}/{\rm SL}_{n+1}$
, which we already proved is stably rational.
$V_{d,n}/{\rm SL}_{n+1}$
, which we already proved is stably rational.
3.2 Abelian
 $3$
-folds
$3$
-folds
Let
![]() $k$
be a field of characteristic not equal to
$k$
be a field of characteristic not equal to
![]() $3$
.
$3$
.
The rational maps
![]() $\mathcal{H}_{4,2}/{\rm PGL}_3 \dashrightarrow \mathcal{M}_3 \dashrightarrow{\mathcal{A}}_3$
over
$\mathcal{H}_{4,2}/{\rm PGL}_3 \dashrightarrow \mathcal{M}_3 \dashrightarrow{\mathcal{A}}_3$
over
![]() $k$
are birational over
$k$
are birational over
![]() $\overline{k}$
(this follows from Torelli and a dimension count) and hence birational over
$\overline{k}$
(this follows from Torelli and a dimension count) and hence birational over
![]() $k$
. Therefore,
$k$
. Therefore,
![]() ${\mathcal{A}}_3$
is stably rational over
${\mathcal{A}}_3$
is stably rational over
![]() $k$
by Theorem3.1. This is sufficient for Theorem1.5.
$k$
by Theorem3.1. This is sufficient for Theorem1.5.
3.3 Abelian 4-folds
Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $0$
. We prove the
$0$
. We prove the
![]() $g=4$
case of Theorem1.3.
$g=4$
case of Theorem1.3.
For the following result we closely follow [Reference Izadi, Lo Giudice and SankaranILS09], which proves the analogous result over
![]() $\mathbb{C}$
, but a few modifications are required. The main difference is that in [Reference Izadi, Lo Giudice and SankaranILS09], the authors work with certain quartic surfaces, and then pass to the double covers of
$\mathbb{C}$
, but a few modifications are required. The main difference is that in [Reference Izadi, Lo Giudice and SankaranILS09], the authors work with certain quartic surfaces, and then pass to the double covers of
![]() ${\mathbb{P}}^3$
ramified along the quartic surface. Some care is needed over non-algebraically closed fields where there may be many such covers given by quadratic twists.
${\mathbb{P}}^3$
ramified along the quartic surface. Some care is needed over non-algebraically closed fields where there may be many such covers given by quadratic twists.
Theorem 3.2.
The coarse moduli space
![]() ${\mathcal{R}}_5$
of étale double covers of a genus
${\mathcal{R}}_5$
of étale double covers of a genus
![]() $5$
curve is unirational over
$5$
curve is unirational over
![]() $k$
. Hence,
$k$
. Hence,
![]() ${\mathcal{A}}_4$
is unirational over
${\mathcal{A}}_4$
is unirational over
![]() $k$
.
$k$
.
In the rest of this section, we prove the first part of this: the second part follows since the Pyrm map
![]() ${\mathcal{R}}_5 \to{\mathcal{A}}_4$
is dominant and defined over
${\mathcal{R}}_5 \to{\mathcal{A}}_4$
is dominant and defined over
![]() $k$
.
$k$
.
Fix five points
![]() $P_1,\dots, P_5 \in{\mathbb{P}}^3(k)$
in linear general position. Without loss of generality,
$P_1,\dots, P_5 \in{\mathbb{P}}^3(k)$
in linear general position. Without loss of generality,
![]() $P_1 =(0:0:0:1)$
. We consider the space
$P_1 =(0:0:0:1)$
. We consider the space
![]() $\mathcal{Q}'\subset{{\rm H}}^0({\mathcal{O}}_{{\mathbb{P}}^3}(4))$
of quartic forms
$\mathcal{Q}'\subset{{\rm H}}^0({\mathcal{O}}_{{\mathbb{P}}^3}(4))$
of quartic forms
![]() $F$
in four variables such that the associated quartic surface
$F$
in four variables such that the associated quartic surface
![]() $X:=\{x\in{\mathbb{P}}^3\mid F(x) = 0\}$
has exactly six ordinary double points over the algebraic closure, at least five of which are
$X:=\{x\in{\mathbb{P}}^3\mid F(x) = 0\}$
has exactly six ordinary double points over the algebraic closure, at least five of which are
![]() $P_1,\dots, P_5$
. This is a quasi-affine variety defined over
$P_1,\dots, P_5$
. This is a quasi-affine variety defined over
![]() $k$
. Moreover, if
$k$
. Moreover, if
![]() $F$
is defined over
$F$
is defined over
![]() $k$
then necessarily the sixth double point is also defined over
$k$
then necessarily the sixth double point is also defined over
![]() $k$
. The key result is as follows.
$k$
. The key result is as follows.
Lemma 3.3.
The space
![]() $\mathcal{Q}'$
is geometrically irreducible and unirational.
$\mathcal{Q}'$
is geometrically irreducible and unirational.
Proof.
We follow [Reference Izadi, Lo Giudice and SankaranILS09, Proposition 2.1], which proves unirationality over the algebraic closure (our
![]() $\mathcal{Q}'$
is the affine cone over the
$\mathcal{Q}'$
is the affine cone over the
![]() $\mathcal{Q}$
appearing in [ILS]). The space of quartic polynomials
$\mathcal{Q}$
appearing in [ILS]). The space of quartic polynomials
![]() $F$
whose associated quartic surface has at least five double points at
$F$
whose associated quartic surface has at least five double points at
![]() $P_1,\dots, P_5$
is a vector space which we denote by
$P_1,\dots, P_5$
is a vector space which we denote by
![]() $V$
. For the sixth double point, consider the scheme
$V$
. For the sixth double point, consider the scheme
The projection onto
![]() ${\mathbb{P}}^3$
is surjective and the fibres are vector spaces (not just affine spaces: there is a section, the zero section). It follows that there is a dense open
${\mathbb{P}}^3$
is surjective and the fibres are vector spaces (not just affine spaces: there is a section, the zero section). It follows that there is a dense open
![]() $U\subset{\mathbb{P}}^3$
over which
$U\subset{\mathbb{P}}^3$
over which
![]() $B_0$
becomes isomorphic to
$B_0$
becomes isomorphic to
![]() $U \times{\mathbb{A}}^n$
for some
$U \times{\mathbb{A}}^n$
for some
![]() $n$
, and therefore
$n$
, and therefore
![]() $B_0$
is rational.
$B_0$
is rational.
The other projection is a map
![]() $B_0 \to V$
whose image contains
$B_0 \to V$
whose image contains
![]() $\mathcal{Q}'$
as a dense open subset. As
$\mathcal{Q}'$
as a dense open subset. As
![]() $B_0$
is rational, we see that
$B_0$
is rational, we see that
![]() $\mathcal{Q}'$
is unirational.
$\mathcal{Q}'$
is unirational.
There is a natural map
![]() $ \varrho \colon \mathcal{Q}' \longrightarrow{\mathcal{R}}_5$
defined in the following way [ILS, Section 1]. For
$ \varrho \colon \mathcal{Q}' \longrightarrow{\mathcal{R}}_5$
defined in the following way [ILS, Section 1]. For
![]() $F\in \mathcal{Q}'$
, let
$F\in \mathcal{Q}'$
, let
![]() $X$
be the associated quartic surface and
$X$
be the associated quartic surface and
the associated quartic double solid. Let
![]() $W_X$
be the blow-up of
$W_X$
be the blow-up of
![]() $\Lambda _X$
at
$\Lambda _X$
at
![]() $(0:0:0:1:0)$
. Then composing the blow-up map with the natural projection to
$(0:0:0:1:0)$
. Then composing the blow-up map with the natural projection to
![]() ${\mathbb{P}}^2$
yields a morphism
${\mathbb{P}}^2$
yields a morphism
![]() $f\colon W_X \to{\mathbb{P}}^2$
. This is a conic bundle morphism whose non-smooth locus
$f\colon W_X \to{\mathbb{P}}^2$
. This is a conic bundle morphism whose non-smooth locus
![]() $C_X \subset{\mathbb{P}}^2$
is a plane sextic curve whose singular points are exactly the images of the singular points of
$C_X \subset{\mathbb{P}}^2$
is a plane sextic curve whose singular points are exactly the images of the singular points of
![]() $X$
(see [ILS, Propositions 1.5 and 1.6]). Thus if
$X$
(see [ILS, Propositions 1.5 and 1.6]). Thus if
![]() $F$
is general,
$F$
is general,
![]() $C_X$
has five ordinary double points, so its normalisation
$C_X$
has five ordinary double points, so its normalisation
![]() $\widetilde{C}_X$
has genus
$\widetilde{C}_X$
has genus
![]() $5$
.
$5$
.
Next let
![]() $S= W_X \times _{{\mathbb{P}}^2} \widetilde{C}_X$
and let
$S= W_X \times _{{\mathbb{P}}^2} \widetilde{C}_X$
and let
![]() $\widetilde{S}$
be the normalisation of
$\widetilde{S}$
be the normalisation of
![]() $S$
. We then apply Stein factorisation to the induced map
$S$
. We then apply Stein factorisation to the induced map
![]() $\widetilde{S} \to \widetilde{C}_X$
to obtain a finite morphism
$\widetilde{S} \to \widetilde{C}_X$
to obtain a finite morphism
![]() $\Gamma _F \to \widetilde{C}_X$
, which by [ILS, Proposition 1.8] is a geometrically connected finite étale cover of degree
$\Gamma _F \to \widetilde{C}_X$
, which by [ILS, Proposition 1.8] is a geometrically connected finite étale cover of degree
![]() $2$
. Thus the pair
$2$
. Thus the pair
![]() $(\widetilde{C}_X, \Gamma _F)$
gives a well-defined element of
$(\widetilde{C}_X, \Gamma _F)$
gives a well-defined element of
![]() ${\mathcal{R}}_5$
. All these constructions are natural, so we define the morphism
${\mathcal{R}}_5$
. All these constructions are natural, so we define the morphism
![]() $\varrho$
by
$\varrho$
by
![]() $\varrho (F)=(\tilde{C}_X,\Gamma _F)$
.
$\varrho (F)=(\tilde{C}_X,\Gamma _F)$
.
To show that
![]() ${\mathcal{R}}_5$
is unirational, we note from [ILS, Corollary 3.3] that
${\mathcal{R}}_5$
is unirational, we note from [ILS, Corollary 3.3] that
![]() $\mathcal{Q}'\to{\mathcal{R}}_5$
is dominant over
$\mathcal{Q}'\to{\mathcal{R}}_5$
is dominant over
![]() $\overline{k}$
, hence it is dominant over
$\overline{k}$
, hence it is dominant over
![]() $k$
, whence
$k$
, whence
![]() ${\mathcal{R}}_5$
is unirational by Lemma 3.3. As
${\mathcal{R}}_5$
is unirational by Lemma 3.3. As
![]() ${\mathcal{R}}_5 \to{\mathcal{A}}_4$
is dominant,
${\mathcal{R}}_5 \to{\mathcal{A}}_4$
is dominant,
![]() ${\mathcal{A}}_4$
is also unirational.
${\mathcal{A}}_4$
is also unirational.
3.4 Abelian 5-folds
Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $0$
. We prove the
$0$
. We prove the
![]() $g=5$
case of Theorem1.3.
$g=5$
case of Theorem1.3.
We proceed as in Section 3.3, this time following [Reference Farkas and VerraFV16, Section 1], which proves the analogous result over
![]() $\mathbb{C}$
. This time the method extends to
$\mathbb{C}$
. This time the method extends to
![]() $k$
with little difficulty.
$k$
with little difficulty.
Theorem 3.4.
The coarse moduli space
![]() ${\mathcal{R}}_6$
of étale double covers of a genus
${\mathcal{R}}_6$
of étale double covers of a genus
![]() $6$
curve is unirational over
$6$
curve is unirational over
![]() $k$
. Hence,
$k$
. Hence,
![]() ${\mathcal{A}}_5$
is unirational over
${\mathcal{A}}_5$
is unirational over
![]() $k$
.
$k$
.
Pick four points
![]() $O_1,\dots, O_4 \in{\mathbb{P}}^2(k)$
in linear general position and let
$O_1,\dots, O_4 \in{\mathbb{P}}^2(k)$
in linear general position and let
![]() $P_i = (O_i,O_i) \in{\mathbb{P}}^2 \times{\mathbb{P}}^2$
. Consider the linear system
$P_i = (O_i,O_i) \in{\mathbb{P}}^2 \times{\mathbb{P}}^2$
. Consider the linear system
![]() ${\mathbb{P}}^{15}$
of hypersurfaces of bidegree
${\mathbb{P}}^{15}$
of hypersurfaces of bidegree
![]() $(2,2)$
in
$(2,2)$
in
![]() ${\mathbb{P}}^2 \times{\mathbb{P}}^2$
that have ordinary double points at
${\mathbb{P}}^2 \times{\mathbb{P}}^2$
that have ordinary double points at
![]() $P_1,\,P_2,\,P_3,\,P_4$
. For such a 3-fold
$P_1,\,P_2,\,P_3,\,P_4$
. For such a 3-fold
![]() $X$
, projecting onto the first factor
$X$
, projecting onto the first factor
![]() ${\mathbb{P}}^2$
induces a conic bundle morphism
${\mathbb{P}}^2$
induces a conic bundle morphism
![]() $X \to{\mathbb{P}}^2$
. The discriminant is a sextic curve
$X \to{\mathbb{P}}^2$
. The discriminant is a sextic curve
![]() $C_X$
whose singularities are generically the image of the singularities of
$C_X$
whose singularities are generically the image of the singularities of
![]() $X$
[Reference Farkas and VerraFV16, Proposition 1.2]. Thus for general
$X$
[Reference Farkas and VerraFV16, Proposition 1.2]. Thus for general
![]() $X$
there are four nodes, so the normalisation
$X$
there are four nodes, so the normalisation
![]() $\widetilde{C}_X$
has genus
$\widetilde{C}_X$
has genus
![]() $6$
. Moreover, applying Stein factorisation to the singular locus as in Section 3.3, we obtain a geometrically connected étale double cover
$6$
. Moreover, applying Stein factorisation to the singular locus as in Section 3.3, we obtain a geometrically connected étale double cover
![]() $\Gamma _X \to \widetilde{C}_X$
. This constructs a rational map
$\Gamma _X \to \widetilde{C}_X$
. This constructs a rational map
![]() ${\mathbb{P}}^{15} \dashrightarrow{\mathcal{R}}_6$
over
${\mathbb{P}}^{15} \dashrightarrow{\mathcal{R}}_6$
over
![]() $k$
. By [Reference Farkas and VerraFV16, Theorem 1.4] this map is dominant, and hence
$k$
. By [Reference Farkas and VerraFV16, Theorem 1.4] this map is dominant, and hence
![]() ${\mathcal{R}}_6$
is unirational. Again
${\mathcal{R}}_6$
is unirational. Again
![]() ${\mathcal{R}}_6 \to{\mathcal{A}}_5$
is dominant, and thus
${\mathcal{R}}_6 \to{\mathcal{A}}_5$
is dominant, and thus
![]() ${\mathcal{A}}_5$
is also unirational.
${\mathcal{A}}_5$
is also unirational.
Combining the results of this section with the results from Section 2.1 completes the proof of Theorem1.3.
4. Weak approximation
4.1
 $k_v$
-points of a stack
$k_v$
-points of a stack
Let
![]() $k$
be a number field and
$k$
be a number field and
![]() $v$
a place of
$v$
a place of
![]() $k$
. For finitely presented algebraic stacks
$k$
. For finitely presented algebraic stacks
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $k_v$
, Christensen [Reference ChristensenChr05, Section 5] gave a topology on
$k_v$
, Christensen [Reference ChristensenChr05, Section 5] gave a topology on
![]() $\mathscr{X}{({k_v})}$
, extending the
$\mathscr{X}{({k_v})}$
, extending the
![]() $v$
-adic topology on the usual
$v$
-adic topology on the usual
![]() $k_v$
-points of schemes. It has the following properties.
$k_v$
-points of schemes. It has the following properties.
-
(i) Any morphism of stacks over
 $k_v$
induces a continuous map on
$k_v$
induces a continuous map on
 $k_v$
-points [Reference ChristensenChr05, Theorem 9.0.3].
$k_v$
-points [Reference ChristensenChr05, Theorem 9.0.3]. -
(ii) Any smooth morphism of stacks over
 $k_v$
induces an open map on
$k_v$
induces an open map on
 $k_v$
-points [Chr, Theorem 11.0.4].
$k_v$
-points [Chr, Theorem 11.0.4].
The topology is unique because Christensen proves in [Chr, Theorem 7.0.7] that any
![]() $k_v$
-point of an algebraic stack is the image of a
$k_v$
-point of an algebraic stack is the image of a
![]() $k_v$
-point under a smooth morphism from some scheme.
$k_v$
-point under a smooth morphism from some scheme.
The following corresponds to the well-known fact that a non-empty
![]() $v$
-adic open subset of a smooth irreducible scheme is Zariski dense, which is an application of the implicit function theorem.
$v$
-adic open subset of a smooth irreducible scheme is Zariski dense, which is an application of the implicit function theorem.
Lemma 4.1.
Let
![]() $\mathscr{X}$
be a smooth finitely presented irreducible algebraic stack over
$\mathscr{X}$
be a smooth finitely presented irreducible algebraic stack over
![]() $k_v$
and let
$k_v$
and let
![]() $W \subseteq \mathscr{X}(k_v)$
be non-empty and open in the
$W \subseteq \mathscr{X}(k_v)$
be non-empty and open in the
![]() $v$
-adic sense above. Then
$v$
-adic sense above. Then
![]() $W$
is dense in
$W$
is dense in
![]() $\mathscr{X}$
.
$\mathscr{X}$
.
Proof.
Let
![]() $f\colon Z \to \mathscr{X}$
be a smooth morphism from a finitely presented irreducible scheme such that
$f\colon Z \to \mathscr{X}$
be a smooth morphism from a finitely presented irreducible scheme such that
![]() $f(Z(k_v)) \cap W \neq{\varnothing }$
; this exists by [Chr, Theorem 7.0.7]. Then
$f(Z(k_v)) \cap W \neq{\varnothing }$
; this exists by [Chr, Theorem 7.0.7]. Then
![]() $f^{-1}(W)$
is a non-empty
$f^{-1}(W)$
is a non-empty
![]() $v$
-adic open set, so it is dense in
$v$
-adic open set, so it is dense in
![]() $Z$
as
$Z$
as
![]() $Z$
is a scheme. However, both
$Z$
is a scheme. However, both
![]() $Z \to \mathscr{X}$
and
$Z \to \mathscr{X}$
and
![]() $Z(k_v) \to \mathscr{X}(k_v)$
are open and continuous. Thus
$Z(k_v) \to \mathscr{X}(k_v)$
are open and continuous. Thus
![]() $f(Z)$
is dense in
$f(Z)$
is dense in
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $f(f^{-1}(W))$
is dense in
$f(f^{-1}(W))$
is dense in
![]() $f(Z)$
, and the result easily follows.
$f(Z)$
, and the result easily follows.
We require the following version of Hensel’s lemma for algebraic stacks.
Lemma 4.2.
Let
![]() $R$
be a complete noetherian local ring, or an excellent Henselian discrete valuation ring, with maximal ideal
$R$
be a complete noetherian local ring, or an excellent Henselian discrete valuation ring, with maximal ideal
![]() $\mathfrak{m}$
. Let
$\mathfrak{m}$
. Let
![]() $\mathscr{X}$
be a smooth algebraic stack over
$\mathscr{X}$
be a smooth algebraic stack over
![]() $R$
. Then for all
$R$
. Then for all
![]() $n \in{\mathbb{N}}$
the natural map
$n \in{\mathbb{N}}$
the natural map
is surjective.
Proof.
Recall that smooth means formally smooth and locally of finite presentation. Formal smoothness (see [SP23, Tag 0DNV]) implies that for any
![]() $n \in{\mathbb{N}}$
and any
$n \in{\mathbb{N}}$
and any
![]() $1$
-commutative diagram
$1$
-commutative diagram

there exists a diagonal arrow making the diagram
![]() $2$
-commutative. It follows that
$2$
-commutative. It follows that
![]() $\mathscr{X}{({R/{\mathfrak{m}}^{n+1}})}\to \mathscr{X}{({R/{\mathfrak{m}}^{n}})}$
is surjective for all
$\mathscr{X}{({R/{\mathfrak{m}}^{n+1}})}\to \mathscr{X}{({R/{\mathfrak{m}}^{n}})}$
is surjective for all
![]() $n \in{\mathbb{N}}$
, and it follows that
$n \in{\mathbb{N}}$
, and it follows that
![]() $\lim _i \mathscr{X}{({R/{\mathfrak{m}}^{n+i}})}\to \mathscr{X}{({R/{\mathfrak{m}}^{n}})}$
is surjective. By effectivity of formal objects [SP23, Lemma 98.9.5, Tag 07X3] we have
$\lim _i \mathscr{X}{({R/{\mathfrak{m}}^{n+i}})}\to \mathscr{X}{({R/{\mathfrak{m}}^{n}})}$
is surjective. By effectivity of formal objects [SP23, Lemma 98.9.5, Tag 07X3] we have
![]() $\lim _i \mathscr{X}(R/{\mathfrak{m}}^{n+i}) = \mathscr{X}(\widehat{R})$
, where
$\lim _i \mathscr{X}(R/{\mathfrak{m}}^{n+i}) = \mathscr{X}(\widehat{R})$
, where
![]() $\widehat{R}$
denotes the completion of
$\widehat{R}$
denotes the completion of
![]() $R$
. Thus if
$R$
. Thus if
![]() $R$
is complete we are done. Otherwise, Artin approximation [Reference ArtinArt69, Theorem 1.12], applied to the functor given by the isomorphism classes of objects of
$R$
is complete we are done. Otherwise, Artin approximation [Reference ArtinArt69, Theorem 1.12], applied to the functor given by the isomorphism classes of objects of
![]() $\mathscr{X}$
, shows that the composition
$\mathscr{X}$
, shows that the composition
![]() $\mathscr{X}(R) \to \mathscr{X}(\widehat{R}) \to \mathscr{X}(R/{\mathfrak{m}}^{n})$
is surjective for any
$\mathscr{X}(R) \to \mathscr{X}(\widehat{R}) \to \mathscr{X}(R/{\mathfrak{m}}^{n})$
is surjective for any
![]() $n$
, as required.
$n$
, as required.
4.2 Weak approximation
Definition 4.3. We say that a finitely presented algebraic stack
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $k$
satisfies weak approximation if the natural map
$k$
satisfies weak approximation if the natural map
![]() $\mathscr{X}^{{\rm sm}}{({k})} \to \prod _v\mathscr{X}^{{\rm sm}}{({k_v})}$
has dense image. (Here
$\mathscr{X}^{{\rm sm}}{({k})} \to \prod _v\mathscr{X}^{{\rm sm}}{({k_v})}$
has dense image. (Here
![]() $\mathscr{X}^{{\rm sm}}$
denotes the smooth locus of
$\mathscr{X}^{{\rm sm}}$
denotes the smooth locus of
![]() $\mathscr{X}$
.)
$\mathscr{X}$
.)
Note that, unlike the case of varieties, the map
![]() $\mathscr{X}{({k})} \to \prod _v\mathscr{X}{({k_v})}$
need not be injective (its injectivity is related to triviality of various Tate–Shafarevich sets). Nevertheless we will sometimes abuse notation and use
$\mathscr{X}{({k})} \to \prod _v\mathscr{X}{({k_v})}$
need not be injective (its injectivity is related to triviality of various Tate–Shafarevich sets). Nevertheless we will sometimes abuse notation and use
![]() $\mathscr{X}{({k})}$
also to denote the image of this map, for instance in Lemma 4.10.
$\mathscr{X}{({k})}$
also to denote the image of this map, for instance in Lemma 4.10.
Lemma 4.4.
![]() $\mathscr{X}$
satisfies weak approximation if and only if either
$\mathscr{X}$
satisfies weak approximation if and only if either
![]() $\prod _v\mathscr{X}^{{\rm sm}}(k_v)$
is empty or, for any finite set
$\prod _v\mathscr{X}^{{\rm sm}}(k_v)$
is empty or, for any finite set
![]() $S$
of places of
$S$
of places of
![]() $k$
and for any non-empty open subset
$k$
and for any non-empty open subset
![]() $W \subseteq \prod _{v \in S} \mathscr{X}^{{\rm sm}}(k_v)$
, there exists an element of
$W \subseteq \prod _{v \in S} \mathscr{X}^{{\rm sm}}(k_v)$
, there exists an element of
![]() $\mathscr{X}(k)$
whose images lies in
$\mathscr{X}(k)$
whose images lies in
![]() $W$
.
$W$
.
Proof. Follows immediately from the definition.
A rational map
![]() $f\colon \mathscr{X}_1 \dashrightarrow \mathscr{X}_2$
of finitely presented algebraic stacks is said to be birational if there exist dense open substacks
$f\colon \mathscr{X}_1 \dashrightarrow \mathscr{X}_2$
of finitely presented algebraic stacks is said to be birational if there exist dense open substacks
![]() $\mathscr{U}_i \subset \mathscr{X}_i$
such that
$\mathscr{U}_i \subset \mathscr{X}_i$
such that
![]() $f$
is defined on
$f$
is defined on
![]() $\mathscr{U}_1$
,
$\mathscr{U}_1$
,
![]() $f(\mathscr{U}_1) \subseteq \mathscr{U}_2$
, and
$f(\mathscr{U}_1) \subseteq \mathscr{U}_2$
, and
![]() $f|_{\mathscr{U}_1}\colon \mathscr{U}_1 \to \mathscr{U}_2$
is an isomorphism. If such a rational map exists, we say that
$f|_{\mathscr{U}_1}\colon \mathscr{U}_1 \to \mathscr{U}_2$
is an isomorphism. If such a rational map exists, we say that
![]() $\mathscr{X}_1$
and
$\mathscr{X}_1$
and
![]() $\mathscr{X}_2$
are birationally equivalent.
$\mathscr{X}_2$
are birationally equivalent.
Weak approximation for smooth stacks is a birationally invariant property.
Lemma 4.5.
Let
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{Y}$
be birationally equivalent smooth irreducible algebraic stacks over
$\mathscr{Y}$
be birationally equivalent smooth irreducible algebraic stacks over
![]() $k$
. Then
$k$
. Then
![]() $\mathscr{X}$
satisfies weak approximation if and only if
$\mathscr{X}$
satisfies weak approximation if and only if
![]() $\mathscr{Y}$
does.
$\mathscr{Y}$
does.
Proof.
It suffices to prove the result in the case where
![]() $\mathscr{X} \to \mathscr{Y}$
is an open immersion. Weak approximation for
$\mathscr{X} \to \mathscr{Y}$
is an open immersion. Weak approximation for
![]() $\mathscr{Y}$
implies weak approximation for
$\mathscr{Y}$
implies weak approximation for
![]() $\mathscr{X}$
as a special case of Lemma 4.6 below. On the other hand, assume that
$\mathscr{X}$
as a special case of Lemma 4.6 below. On the other hand, assume that
![]() $\mathscr{X}$
satisfies weak approximation. If
$\mathscr{X}$
satisfies weak approximation. If
![]() $\prod _v \mathscr{Y}(k_v) ={\varnothing }$
, there is nothing to prove. Otherwise, let
$\prod _v \mathscr{Y}(k_v) ={\varnothing }$
, there is nothing to prove. Otherwise, let
![]() $W \subseteq \prod _{v \in S} \mathscr{Y}(k_v)$
as in Lemma 4.4. It suffices to show that
$W \subseteq \prod _{v \in S} \mathscr{Y}(k_v)$
as in Lemma 4.4. It suffices to show that
![]() $W \cap \mathscr{X} \neq{\varnothing }$
. However, this is Lemma 4.1 applied to
$W \cap \mathscr{X} \neq{\varnothing }$
. However, this is Lemma 4.1 applied to
![]() $\mathscr{Y}$
.
$\mathscr{Y}$
.
In particular, if
![]() $\mathscr{X}$
admits an open dense substack
$\mathscr{X}$
admits an open dense substack
![]() $U$
that is isomorphic to a scheme, then weak approximation for
$U$
that is isomorphic to a scheme, then weak approximation for
![]() $\mathscr{X}$
is equivalent to weak approximation for the scheme
$\mathscr{X}$
is equivalent to weak approximation for the scheme
![]() $U$
, and the definition does not offer anything new. Therefore, to get interesting new problems in general one should consider stacks with non-trivial generic stabilisers; such stacks typically admit open substacks that are gerbes over a scheme. In such cases one may hope to prove weak approximation using the following fibration result, which is a stacky version of [Reference Colliot-Thélène and GilleC-TG04, Proposition 1.1].
$U$
, and the definition does not offer anything new. Therefore, to get interesting new problems in general one should consider stacks with non-trivial generic stabilisers; such stacks typically admit open substacks that are gerbes over a scheme. In such cases one may hope to prove weak approximation using the following fibration result, which is a stacky version of [Reference Colliot-Thélène and GilleC-TG04, Proposition 1.1].
Lemma 4.6.
Let
![]() $f\colon \mathscr{X} \to \mathscr{Y}$
be a smooth morphism of smooth irreducible algebraic stacks over
$f\colon \mathscr{X} \to \mathscr{Y}$
be a smooth morphism of smooth irreducible algebraic stacks over
![]() $k$
. Assume that
$k$
. Assume that
![]() $\mathscr{Y}$
satisfies weak approximation and that the fibre over every rational point of
$\mathscr{Y}$
satisfies weak approximation and that the fibre over every rational point of
![]() $\mathscr{Y}$
is everywhere locally soluble and satisfies weak approximation. Then
$\mathscr{Y}$
is everywhere locally soluble and satisfies weak approximation. Then
![]() $\mathscr{X}$
satisfies weak approximation.
$\mathscr{X}$
satisfies weak approximation.
Proof.
If
![]() $\prod _v \mathscr{X}(k_v) ={\varnothing }$
, there is nothing to prove. Otherwise let
$\prod _v \mathscr{X}(k_v) ={\varnothing }$
, there is nothing to prove. Otherwise let
![]() $W \subseteq \prod _{v \in S} \mathscr{X}(k_v)$
as in Lemma 4.4. As
$W \subseteq \prod _{v \in S} \mathscr{X}(k_v)$
as in Lemma 4.4. As
![]() $f$
is smooth the image
$f$
is smooth the image
![]() $f(W) \subseteq \prod _{v \in S} \mathscr{Y}(k_v)$
is open. So let
$f(W) \subseteq \prod _{v \in S} \mathscr{Y}(k_v)$
is open. So let
![]() $y \in \mathscr{Y}(k)$
with image in
$y \in \mathscr{Y}(k)$
with image in
![]() $f(W)$
. Then
$f(W)$
. Then
![]() $f^{-1}(y) \cap W \neq{\varnothing }$
and
$f^{-1}(y) \cap W \neq{\varnothing }$
and
![]() $f^{-1}(y)$
is everywhere locally soluble and satisfies weak approximation, and thus
$f^{-1}(y)$
is everywhere locally soluble and satisfies weak approximation, and thus
![]() $f^{-1}(y) \cap W$
contains a rational point, as required.
$f^{-1}(y) \cap W$
contains a rational point, as required.
For neutral affine gerbes, weak approximation is equivalent to a statement in Galois cohomology.
Lemma 4.7.
Let
![]() $G$
be a finite type affine group scheme over
$G$
be a finite type affine group scheme over
![]() $k$
. Then
$k$
. Then
![]() $BG$
satisfies weak approximation if and only if the natural map
$BG$
satisfies weak approximation if and only if the natural map
is surjective for all finite sets of places
![]() $S$
of
$S$
of
![]() $k$
.
$k$
.
Proof.
Recall that for any field extension
![]() $k \subset L$
we have
$k \subset L$
we have
![]() $BG{({L})} ={{\rm H}}^1(L,G)$
, since both sets classify
$BG{({L})} ={{\rm H}}^1(L,G)$
, since both sets classify
![]() $G_L$
torsors over
$G_L$
torsors over
![]() $L$
. The set
$L$
. The set
![]() ${{\rm H}}^1(k_v,G)$
is finite [Reference Platonov and RapinchukPR94, Theorem 6.14] and the induced topology is simply the discrete topology. Therefore, it suffices to note that a subset of a product of discrete sets is dense if and only if it surjects onto any finite collection of factors.
${{\rm H}}^1(k_v,G)$
is finite [Reference Platonov and RapinchukPR94, Theorem 6.14] and the induced topology is simply the discrete topology. Therefore, it suffices to note that a subset of a product of discrete sets is dense if and only if it surjects onto any finite collection of factors.
We emphasise that for a general algebraic stack
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $\mathbb{Q}$
it can happen that its coarse moduli space
$\mathbb{Q}$
it can happen that its coarse moduli space
![]() $\mathcal{X}$
satisfies weak approximation but
$\mathcal{X}$
satisfies weak approximation but
![]() $\mathscr{X}$
itself does not.
$\mathscr{X}$
itself does not.
Example 4.8. Take
![]() $\mathscr{X} = B{\mathbb{Z}}/8{\mathbb{Z}}$
. Then the associated coarse moduli space is just
$\mathscr{X} = B{\mathbb{Z}}/8{\mathbb{Z}}$
. Then the associated coarse moduli space is just
![]() ${\rm Spec}{\mathbb{Q}}$
, which trivially satisfies weak approximation. But
${\rm Spec}{\mathbb{Q}}$
, which trivially satisfies weak approximation. But
![]() $B{\mathbb{Z}}/8{\mathbb{Z}}$
fails weak approximation (the famous example of Wang [Reference WangWan48]): there is no
$B{\mathbb{Z}}/8{\mathbb{Z}}$
fails weak approximation (the famous example of Wang [Reference WangWan48]): there is no
![]() ${\mathbb{Z}}/8{\mathbb{Z}}$
-extension of
${\mathbb{Z}}/8{\mathbb{Z}}$
-extension of
![]() $\mathbb{Q}$
that realises the unique unramified
$\mathbb{Q}$
that realises the unique unramified
![]() ${\mathbb{Z}}/8{\mathbb{Z}}$
-extension of
${\mathbb{Z}}/8{\mathbb{Z}}$
-extension of
![]() ${\mathbb{Q}}_2$
.
${\mathbb{Q}}_2$
.
For
![]() $G=\mu _2$
, however, which is the case relevant to us, there is no such problem.
$G=\mu _2$
, however, which is the case relevant to us, there is no such problem.
Lemma 4.9.
If
![]() $\mu _n \subset k$
, then
$\mu _n \subset k$
, then
![]() $B \mu _n$
satisfies weak approximation.
$B \mu _n$
satisfies weak approximation.
Proof.
By Kummer theory we have
![]() ${{\rm H}}^1(k,\mu _n) = k^\times /k^{\times n}$
, and similarly for
${{\rm H}}^1(k,\mu _n) = k^\times /k^{\times n}$
, and similarly for
![]() $k_v$
. It thus suffices to apply Lemma 4.7 and note that weak approximation for
$k_v$
. It thus suffices to apply Lemma 4.7 and note that weak approximation for
![]() $k$
implies that
$k$
implies that
![]() $k^\times /k^{\times n} \to \prod _{v \in S} k_v^\times / k_v^{\times n}$
is surjective.
$k^\times /k^{\times n} \to \prod _{v \in S} k_v^\times / k_v^{\times n}$
is surjective.
From Hensel’s lemma we obtain the following application of weak approximation.
Lemma 4.10.
Let
![]() $\mathscr{X}$
be a smooth irreducible finitely presented algebraic stack over
$\mathscr{X}$
be a smooth irreducible finitely presented algebraic stack over
![]() $k$
with
$k$
with
![]() $\prod _v\mathscr{X}(k_v) \neq{\varnothing }$
that satisfies weak approximation, and
$\prod _v\mathscr{X}(k_v) \neq{\varnothing }$
that satisfies weak approximation, and
![]() $S$
a finite collection of non-zero prime ideals of
$S$
a finite collection of non-zero prime ideals of
![]() $k$
. Let
$k$
. Let
![]() $\mathscr{X}_{{\mathcal{O}}_k}$
be a model of
$\mathscr{X}_{{\mathcal{O}}_k}$
be a model of
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() ${\mathcal{O}}_k$
that is smooth over all elements of
${\mathcal{O}}_k$
that is smooth over all elements of
![]() $S$
. Then the map
$S$
. Then the map
is surjective.
Proof.
We first note that the map
![]() $\prod _{\mathfrak{p} \in S}\mathscr{X}_{{\mathcal{O}}_k}({\mathcal{O}}_{\mathfrak{p}})\to \prod _{\mathfrak{p} \in S} \mathscr{X}_{{\mathcal{O}}_k}({\mathbb{F}}_{\mathfrak{p}})$
is surjective for all
$\prod _{\mathfrak{p} \in S}\mathscr{X}_{{\mathcal{O}}_k}({\mathcal{O}}_{\mathfrak{p}})\to \prod _{\mathfrak{p} \in S} \mathscr{X}_{{\mathcal{O}}_k}({\mathbb{F}}_{\mathfrak{p}})$
is surjective for all
![]() $\mathfrak{p} \in S$
: this follows from Hensel’s lemma for stacks, Lemma 4.2. Moreover, the map
$\mathfrak{p} \in S$
: this follows from Hensel’s lemma for stacks, Lemma 4.2. Moreover, the map
![]() $\mathscr{X}_{{\mathcal{O}}_k}({\mathcal{O}}_{\mathfrak{p}}) \to \mathscr{X}_{{\mathcal{O}}_k}({\mathbb{F}}_{\mathfrak{p}})$
is continuous as
$\mathscr{X}_{{\mathcal{O}}_k}({\mathcal{O}}_{\mathfrak{p}}) \to \mathscr{X}_{{\mathcal{O}}_k}({\mathbb{F}}_{\mathfrak{p}})$
is continuous as
![]() ${\mathcal{O}}_{\mathfrak{p}}\to{\mathbb{F}}_{\mathfrak{p}}$
is continuous [Chr, Proposition 9.0.4]. As
${\mathcal{O}}_{\mathfrak{p}}\to{\mathbb{F}}_{\mathfrak{p}}$
is continuous [Chr, Proposition 9.0.4]. As
![]() $\mathscr{X}_{{\mathcal{O}}_k}({\mathbb{F}}_{\mathfrak{p}})$
is discrete, we find that the fibre of a point is an open subset of
$\mathscr{X}_{{\mathcal{O}}_k}({\mathbb{F}}_{\mathfrak{p}})$
is discrete, we find that the fibre of a point is an open subset of
![]() $\mathscr{X}(k_{\mathfrak{p}})$
. Lemma 4.4 thus implies that it contains a rational point, as required.
$\mathscr{X}(k_{\mathfrak{p}})$
. Lemma 4.4 thus implies that it contains a rational point, as required.
4.3 Weak approximation for
 $\mathscr{A}_2$
$\mathscr{A}_2$
Before turning to
![]() $\mathscr{A}_3$
, we briefly consider the simpler case of
$\mathscr{A}_3$
, we briefly consider the simpler case of
![]() $\mathscr{A}_2$
, where weak approximation holds. To see this, we first note that the natural map
$\mathscr{A}_2$
, where weak approximation holds. To see this, we first note that the natural map
![]() $\mathscr{M}_2 \to \mathscr{A}_2$
is birational. Indeed, the induced map on coarse moduli spaces is birational, and furthermore the map on generic stabilisers is an isomorphism: this is the strong Torelli theorem given (by Serre) in [Reference LauterLau01, Théorème 3].
$\mathscr{M}_2 \to \mathscr{A}_2$
is birational. Indeed, the induced map on coarse moduli spaces is birational, and furthermore the map on generic stabilisers is an isomorphism: this is the strong Torelli theorem given (by Serre) in [Reference LauterLau01, Théorème 3].
Therefore, by Lemma 4.5 it suffices to prove that
![]() $\mathscr{M}_2$
satisfies weak approximation. However, an element of
$\mathscr{M}_2$
satisfies weak approximation. However, an element of
![]() $\mathscr{M}_2(k_v)$
is represented by a hyperelliptic curve over
$\mathscr{M}_2(k_v)$
is represented by a hyperelliptic curve over
![]() $k_v$
, and one can approximate this to an arbitrary precision by a hyperelliptic curve over
$k_v$
, and one can approximate this to an arbitrary precision by a hyperelliptic curve over
![]() $k$
by simply approximating the coefficients (similarly for any finite collection of places).
$k$
by simply approximating the coefficients (similarly for any finite collection of places).
A similar proof also shows that
![]() $\mathscr{A}_1$
satisfies weak approximation.
$\mathscr{A}_1$
satisfies weak approximation.
4.4 Weak approximation for
 $\mathscr{A}_3$
$\mathscr{A}_3$
By Theorem1.5 we know that
![]() ${\mathcal{A}}_3$
is stably rational over
${\mathcal{A}}_3$
is stably rational over
![]() $\mathbb{Q}$
, and hence satisfies weak approximation [Reference Colliot-Thélène and GilleC-TG04, Proposition 1.2].
$\mathbb{Q}$
, and hence satisfies weak approximation [Reference Colliot-Thélène and GilleC-TG04, Proposition 1.2].
Let us briefly consider how one would try to use this to prove that
![]() $\mathscr{A}_3$
satisfies weak approximation, and some of the subtleties that arise. Let
$\mathscr{A}_3$
satisfies weak approximation, and some of the subtleties that arise. Let
![]() $h\colon \mathscr{A}_3 \to{\mathcal{A}}_3$
be the coarse moduli map. Let
$h\colon \mathscr{A}_3 \to{\mathcal{A}}_3$
be the coarse moduli map. Let
![]() $k$
be a number field and
$k$
be a number field and
![]() $S$
a finite set of places of
$S$
a finite set of places of
![]() $k$
. For
$k$
. For
![]() $v \in S$
let
$v \in S$
let
![]() $A_v \in \mathscr{A}_3(k_v)$
. Then there exists a
$A_v \in \mathscr{A}_3(k_v)$
. Then there exists a
![]() $k$
-rational point
$k$
-rational point
![]() $a \in{\mathcal{A}}_3(k)$
arbitrarily close to
$a \in{\mathcal{A}}_3(k)$
arbitrarily close to
![]() $a_v:=h(A_v)$
. The first issue that arises is that there is no guarantee that the fibre
$a_v:=h(A_v)$
. The first issue that arises is that there is no guarantee that the fibre
![]() $h^{-1}(a)$
contains a rational point; in classical parlance
$h^{-1}(a)$
contains a rational point; in classical parlance
![]() $k$
is a field of moduli for
$k$
is a field of moduli for
![]() $a$
, but there is no guarantee that
$a$
, but there is no guarantee that
![]() $k$
is a field of definition for
$k$
is a field of definition for
![]() $a$
. Assuming that we overcome this issue and find
$a$
. Assuming that we overcome this issue and find
![]() $A \in \mathscr{A}_3(k)$
with
$A \in \mathscr{A}_3(k)$
with
![]() $h(A) = a$
, the second issue is as follows: we have that
$h(A) = a$
, the second issue is as follows: we have that
![]() $h(A)$
is close to each
$h(A)$
is close to each
![]() $h(A_v)$
, but this does not guarantee that
$h(A_v)$
, but this does not guarantee that
![]() $A$
is close to the
$A$
is close to the
![]() $A_v$
; in classical parlance this means that we can only guarantee that
$A_v$
; in classical parlance this means that we can only guarantee that
![]() $A$
is close to some Galois twist of the
$A$
is close to some Galois twist of the
![]() $A_v$
, and not our original
$A_v$
, and not our original
![]() $A_v$
.
$A_v$
.
To overcome these issues we need to understand both the generic field of definition and the generic Galois twist. This is achieved by the following result of Shimura [Reference ShimuraShi72] reformulated in stacky language. (See [Reference Bresciani and VistoliBV24] for further applications of stacks to field of moduli questions.)
Lemma 4.11.
Let
![]() $g \in{\mathbb{N}}$
and
$g \in{\mathbb{N}}$
and
![]() $h\colon \mathscr{A}_g \to{\mathcal{A}}_g$
be the coarse moduli map. There exists a dense open subset
$h\colon \mathscr{A}_g \to{\mathcal{A}}_g$
be the coarse moduli map. There exists a dense open subset
![]() $V \subset{\mathcal{A}}_g$
such that
$V \subset{\mathcal{A}}_g$
such that
![]() $U:=h^{-1}(V) \to V$
is a
$U:=h^{-1}(V) \to V$
is a
![]() $\mu _2$
-gerbe. This gerbe is neutral if and only if
$\mu _2$
-gerbe. This gerbe is neutral if and only if
![]() $g$
is odd.
$g$
is odd.
Proof.
It is well known that the generic ppav has automorphism group
![]() $\mu _2$
; this implies that the generic fibre is a
$\mu _2$
; this implies that the generic fibre is a
![]() $\mu _2$
-gerbe and one finds
$\mu _2$
-gerbe and one finds
![]() $V$
by spreading out, cf. [Reference PoonenPoo17, Section 3.2].
$V$
by spreading out, cf. [Reference PoonenPoo17, Section 3.2].
It remains to show that the generic gerbe is neutral if and only if
![]() $g$
is odd. Let
$g$
is odd. Let
![]() $K$
be the function field of
$K$
be the function field of
![]() ${\mathcal{A}}_g$
. Then the generic gerbe is neutral if and only if the generic fibre has a
${\mathcal{A}}_g$
. Then the generic gerbe is neutral if and only if the generic fibre has a
![]() $K$
-point, which means exactly that the generic ppav has a model over
$K$
-point, which means exactly that the generic ppav has a model over
![]() $K$
. The main result of [Reference ShimuraShi72] says that this happens if and only if
$K$
. The main result of [Reference ShimuraShi72] says that this happens if and only if
![]() $g$
is odd, as required.
$g$
is odd, as required.
Proof of Theorem1.6
By Lemma 4.11 we know that
![]() $\mathscr{A}_3$
is birational to a neutral
$\mathscr{A}_3$
is birational to a neutral
![]() $\mu _2$
-gerbe over
$\mu _2$
-gerbe over
![]() ${\mathcal{A}}_3$
. The latter satisfies weak approximation, and the fibres have rational points and satisfy weak approximation by Lemma 4.9. Thus the result follows from Lemmas 4.5 and 4.6.
${\mathcal{A}}_3$
. The latter satisfies weak approximation, and the fibres have rational points and satisfy weak approximation by Lemma 4.9. Thus the result follows from Lemmas 4.5 and 4.6.
Remark 4.12. Our proof makes essential use of the fact that
![]() $g=3$
is odd. In fact, the proof as written does not apply in the apparently easier case of
$g=3$
is odd. In fact, the proof as written does not apply in the apparently easier case of
![]() $g=2$
from Section 4.3, where Shimura showed that the generic hyperelliptic curve of even genus does not descend to its field of moduli [Reference ShimuraShi72, Theorem 3]. Then one might wonder whether, on the contrary, the simple proof for
$g=2$
from Section 4.3, where Shimura showed that the generic hyperelliptic curve of even genus does not descend to its field of moduli [Reference ShimuraShi72, Theorem 3]. Then one might wonder whether, on the contrary, the simple proof for
![]() $g=2$
can be adapted to the case of
$g=2$
can be adapted to the case of
![]() $g=3$
. This does not seem possible either since a key difference is that the map
$g=3$
. This does not seem possible either since a key difference is that the map
![]() $\mathscr{M}_3\to \mathscr{A}_3$
is no longer birational, despite inducing a birational map on the coarse moduli spaces, because the generic stabilisers no longer agree. The following lemma gives an arithmetic manifestation of this phenomenon.
$\mathscr{M}_3\to \mathscr{A}_3$
is no longer birational, despite inducing a birational map on the coarse moduli spaces, because the generic stabilisers no longer agree. The following lemma gives an arithmetic manifestation of this phenomenon.
Lemma 4.13.
Let
![]() $k$
be a field and
$k$
be a field and
![]() $C$
a smooth quartic curve over
$C$
a smooth quartic curve over
![]() $k$
. Then for each separable quadratic extension
$k$
. Then for each separable quadratic extension
![]() $k \subset L$
there exists a principally polarised abelian
$k \subset L$
there exists a principally polarised abelian
![]() $3$
-fold
$3$
-fold
![]() $A$
over
$A$
over
![]() $k$
such that
$k$
such that
![]() $A_L \cong J(C)_L$
but
$A_L \cong J(C)_L$
but
![]() $A$
is not in the image of map
$A$
is not in the image of map
![]() $\mathscr{M}_3(k) \to \mathscr{A}_3(k)$
.
$\mathscr{M}_3(k) \to \mathscr{A}_3(k)$
.
Proof.
The strong Torelli theorem [Reference LauterLau01, Théorème 3] mentioned in Section 4.3 shows that
![]() ${\rm Aut}\, J(C) = {\rm Aut}\,C \oplus{\mathbb{Z}}/2{\mathbb{Z}}$
. As
${\rm Aut}\, J(C) = {\rm Aut}\,C \oplus{\mathbb{Z}}/2{\mathbb{Z}}$
. As
![]() ${{\rm H}}^1(k,{\mathbb{Z}}/2{\mathbb{Z}})$
parametrises separable quadratic extensions of
${{\rm H}}^1(k,{\mathbb{Z}}/2{\mathbb{Z}})$
parametrises separable quadratic extensions of
![]() $k$
, we see that for each such extension
$k$
, we see that for each such extension
![]() $k \subset L$
there is a quadratic twist
$k \subset L$
there is a quadratic twist
![]() $A$
of
$A$
of
![]() $J(C)$
by
$J(C)$
by
![]() $L$
. Such a twist cannot arise from any twist of
$L$
. Such a twist cannot arise from any twist of
![]() $C$
, and thus
$C$
, and thus
![]() $A$
is not the Jacobian of any curve of genus
$A$
is not the Jacobian of any curve of genus
![]() $3$
over
$3$
over
![]() $k$
.
$k$
.
Proof of Theorem1.2
As
![]() $g \geq 7$
the coarse moduli space has general type. Let
$g \geq 7$
the coarse moduli space has general type. Let
![]() $p$
be a prime. To prove the result we will compare the cardinalities of the two sets
$p$
be a prime. To prove the result we will compare the cardinalities of the two sets
The set
![]() $I_1$
is simply the collection of elements of
$I_1$
is simply the collection of elements of
![]() ${\mathcal{A}}_g({\mathbb{F}}_p)$
that arise from some ppav over
${\mathcal{A}}_g({\mathbb{F}}_p)$
that arise from some ppav over
![]() ${\mathbb{F}}_p$
. The set
${\mathbb{F}}_p$
. The set
![]() $I_2$
is the collection of elements of
$I_2$
is the collection of elements of
![]() ${\mathcal{A}}_g({\mathbb{F}}_p)$
that arise as the reduction modulo
${\mathcal{A}}_g({\mathbb{F}}_p)$
that arise as the reduction modulo
![]() $p$
of a ppav over
$p$
of a ppav over
![]() $\mathbb{Q}$
with good reduction at
$\mathbb{Q}$
with good reduction at
![]() $p$
(note that
$p$
(note that
![]() $I_2 \subseteq I_1$
). We will show that
$I_2 \subseteq I_1$
). We will show that
![]() $I_1$
has more elements than
$I_1$
has more elements than
![]() $I_2$
for all sufficiently large
$I_2$
for all sufficiently large
![]() $p$
.
$p$
.
Firstly, the Lang–Weil estimates [Reference Lang and WeilLW54] imply that
![]() $|{\mathcal{A}}_g({\mathbb{F}}_p)| \sim p^m$
as
$|{\mathcal{A}}_g({\mathbb{F}}_p)| \sim p^m$
as
![]() $p \to \infty$
, where
$p \to \infty$
, where
![]() $m = g(g+1)/2 = \dim{\mathcal{A}}_g$
. By Lemma 4.11, spreading out, and the Lang–Weil estimates, we have
$m = g(g+1)/2 = \dim{\mathcal{A}}_g$
. By Lemma 4.11, spreading out, and the Lang–Weil estimates, we have
However, a
![]() $\mu _2$
-gerbe over
$\mu _2$
-gerbe over
![]() ${\mathbb{F}}_p$
is necessarily neutral: indeed,
${\mathbb{F}}_p$
is necessarily neutral: indeed,
![]() $\mu _2$
-gerbes are classified by
$\mu _2$
-gerbes are classified by
![]() ${{\rm H}}_{fppf}^2({\mathbb{F}}_p,\mu _2)$
[Reference OlssonOls16, Theorem 12.2.8]. But Kummer theory implies that
${{\rm H}}_{fppf}^2({\mathbb{F}}_p,\mu _2)$
[Reference OlssonOls16, Theorem 12.2.8]. But Kummer theory implies that
![]() ${{\rm H}}_{fppf}^2({\mathbb{F}}_p,\mu _2) = ({\rm Br}\,{\mathbb{F}}_p)[2]$
, which is trivial as
${{\rm H}}_{fppf}^2({\mathbb{F}}_p,\mu _2) = ({\rm Br}\,{\mathbb{F}}_p)[2]$
, which is trivial as
![]() ${\rm Br}\,{\mathbb{F}}_p = 0$
. We therefore deduce that
${\rm Br}\,{\mathbb{F}}_p = 0$
. We therefore deduce that
![]() $|I_1| \sim p^m$
as
$|I_1| \sim p^m$
as
![]() $p \to \infty$
$p \to \infty$
For
![]() $I_2$
, as
$I_2$
, as
![]() ${\mathcal{A}}_g$
has general type, the Bombieri–Lang conjecture [Reference PoonenPoo17, Conjecture 9.5.11] predicts that
${\mathcal{A}}_g$
has general type, the Bombieri–Lang conjecture [Reference PoonenPoo17, Conjecture 9.5.11] predicts that
![]() ${\mathcal{A}}_g({\mathbb{Q}})$
is not Zariski dense. Thus the Lang–Weil estimates imply that
${\mathcal{A}}_g({\mathbb{Q}})$
is not Zariski dense. Thus the Lang–Weil estimates imply that
![]() $|I_2| = O(p^{m-1})$
. Altogether we deduce that for all sufficiently large primes
$|I_2| = O(p^{m-1})$
. Altogether we deduce that for all sufficiently large primes
![]() $p$
we have
$p$
we have
![]() $|I_1| \gt |I_2|$
, which concludes the proof.
$|I_1| \gt |I_2|$
, which concludes the proof.
Acknowledgements
We are grateful to Christian Böhning, Davide Lombardo and Siddharth Mathur for useful discussions. Christian largely taught us how to prove Theorem1.5. We are also grateful to David Masser and Umberto Zannier, who asked about the unirationality of
![]() ${\mathcal{A}}_4$
, and to the referee for useful comments.
${\mathcal{A}}_4$
, and to the referee for useful comments.
Conflicts of Interest
None
Financial Support
Daniel Loughran was supported by UKRI Future Leaders Fellowship MR/V021362/1.
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.