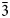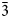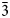Introduction
Bismuth chalcogenides are long known for their pronounced degree of metallic bonding in their structures, a prominent example thereof being tetradymite, Bi2Te2S (Pauling, Reference Pauling1975). They are the subject of intensive interest in materials science, with the ‘archetypal tetradymites’ Bi2Se3, Bi2Te3 and Sb2Te3 (Cook et al., Reference Cook, Ciobanu, Wagner and Stanley2007; Heremans et al., Reference Heremans, Cava and Samarth2017). The tetradymites (in the materials-science sense) are one of the most promising groups of thermoelectric materials, designed to convert waste heat into electricity (Yamini et al., Reference Yamini, Santos, Fortulan, Gazder, Malhotra, Vashaee, Serhiienko and Mori2023). Tuning of the properties, either via variations in the elemental ratios or modification of crystal structures, could enhance the thermoelectric effect and lead to greater applicability (Pathak et al., Reference Pathak, Dutta, Srivastava, Rawat, Gopal, Singh, Soni and Biswas2022). The discovery of new crystal structures of this type, however, is not restricted to the chemical laboratories. New sulfide phases are being reported from Nature, some with previously known and some with novel structures (Kuribayashi et al., Reference Kuribayashi, Nagase, Nozaki, Ishibashi, Shimada, Shimizu and Momma2019; Bindi et al., Reference Bindi, Keutsch, Topa, Kolitsch, Morana and Tait2023; Sejkora et al., Reference Sejkora, Biagioni, Škácha and Mauro2023a, Reference Sejkora, Biagioni, Škácha, Musetti, Kasatkin and Nestola2023b). The description of new minerals from this group of phases could inspire the development of thermoelectric materials.
In this work, we are reporting the properties and crystal structure of a new bismuth chalcogenide discovered in Nature. Its mineral assemblage and mode of occurrence suggest how it could be prepared in the laboratory and this phase could be of interest for novel types of thermoelectric materials. The modulated crystal structure can be rationalised and compared to other chemically related phases in the bismuth–sulfide system. The new mineral, zipserite, and its symbol zps were approved by the Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2022–075, Majzlan et al., Reference Majzlan, Ozdín, Sejkora, Steciuk, Plášil, Rößler and Matthes2022).
The name zipserite honours Kristián Andrej (or also Christian Andreas) Zipser (born November 25, 1783, Györ, Hungary, died February 20, 1864, Banská Bystrica, Slovakia), a prominent mineralogist of the Austro-Hungarian Empire in the 19th Century. He contributed significantly to the establishment of the second oldest Mineralogical Society in the world (1811, Banská Štiavnica, Slovakia), which is followed by today's Slovak Mineralogical Society. Zipser was a member of more than 80 scientific societies and museums and an honorary doctor of several European universities. For his activities, Zipser gained great authority throughout Europe, resulting in several foreign orders and awards from European emperors, kings and dukes. He collected many hand specimens of minerals, which he sent free of charge to museums, universities, institutes, scientists and monarchs, thus significantly enriching the collections of institutions in almost all countries in Europe and North America.
The holotype material (polished section) is deposited in the Mineralogical Museum of Comenius University, Faculty of Natural Sciences in Bratislava, Slovakia, under catalogue number MMUK 7670.
Occurrence and mineral description
Occurrence
Zipserite was found in samples with bismuth sulfotellurides, taken from the tailings pile of the Alsó-Rózsa adit, ~5 km ENE of the village Nagybörzsöny in Hungary (GPS coordinates: 47°56′27″N, 18°53′40″E). Hydrothermal base-metal and precious metal mineralisation are developed in this deposit in andesites to dacites of Miocene age, and are related to the asthenospheric upwelling and subduction of the European platform under the African plate during the last stages of the convergent Alpine collision (Bezák et al., Reference Bezák, Bielik, Marko, Zahorec, Pašteka, Vozár and Papčo2023; Hurai et al., Reference Hurai, Huraiová, Nemec, Konečný and Reato2023). The mineralisation forms veins in andesitic rocks but changes to veinlet zones and disseminations in dacites. The dump material is formed by intensively hydrothermally altered volcanic rocks. The main alteration is propylitisation, which results in the original rocks being changed into a mixture of predominantly white sheet silicates with disseminated sulfides and sulfosalts. Two stages of mineralisation were distinguished: the first stage is represented by pyrite, galena, sphalerite, chalcopyrite and pyrrhotite, and the second one mainly by arsenopyrite, bismuth, bismuthinite, sulfosalts, gold, baryte and carbonates. Of the various selenium tellurides, the tetradymite minerals pilsenite, ikunolite, tetradymite, joséite-A and joséite-B are present, in addition to other Au–Ag–Bi–Te minerals (jonassonite, petzite, hessite and jaszczakite) (Koch and Grassely, Reference Koch and Grasselly1952; Paar et al., Reference Paar, Putz, Topa, Roberts, Stanley and Culetto2006; Pantó and Mikó, Reference Pantó and Mikó1964; Szakáll, Reference Szakáll2002). Szakáll et al. (Reference Szakáll, Zajzon and Kristály2012) described “unusual ikunolite” from Nagybörzsöny. Its composition, normalised to 4 S atoms, is Bi5.29S4 and Bi5.12S4. The structural data were obtained by powder X-ray diffraction, but, given the great degree of similarity among the various Bi–S phases, the “unusual ikunolite” could have actually been zipserite.
The specimens that contain zipserite also contain abundant bismuthinite and native bismuth (Fig. 1) and rare ikunolite and joséite-A. Zipserite is located particularly along the contact between bismuth and bismuthinite, suggesting that it may be a reaction product of these two minerals. Textural evidence suggests that bismuth was the first mineral in the association, and later fluids that brought both Bi and S attacked the early bismuth, and produced zipserite locally. The composition of the altered rocks was not investigated in detail. A peculiar property of these rocks, when embedded in epoxy and prepared as polished sections, is that the rocks expand and crack the sections within a few years. We assume that the altered rocks contain a substantial fraction of smectites that pick up humidity from the air and expand.

Figure 1. Optical and back-scattered electron (BSE) images of the assemblage of bismuth minerals from Nagybörzsöny, Hungary. (a) Reflected light, one Nicol. Note that the reflectance and colour of zipserite and bismuthinite are very similar. A small BSE image was adjusted to match the orientation and size of the reflected-light image. The dashed lines are guides for the eye. (b) Reflected light, partially crossed Nicols, the same area as shown in (a). Note the dark blue colours of the anisotropy of zipserite. (c) BSE image of the intergrowth of native bismuth, bismuthinite and zipserite. The same image (zoomed out, rotated) was also used in (a). The section used is #AR2-3e, the holotype material, deposited under the catalogue number MMUK 7670 at the Comenius University in Bratislava.
Physical and optical properties
Zipserite forms large (up to 500 μm) inclusions in aggregates of bismuth and bismuthinite (Fig. 1). Some of these inclusions seem to be subhedral, lath-like crystals. The colour is silvery, identical to the colour of bismuthinite. Zipserite has a metallic lustre. Hardness is low, estimated as 2–2½, similar to bismuthinite, based on no difference in polishing hardness observed in reflected light. Neither cleavage nor parting was observed owing to the small size of the grains and their intergrowth with other Bi minerals. Density calculated from crystallographic data and empirical formula (see below) is 7.815 g⋅cm–3. Attempts to extract zipserite grains for X-ray diffraction (XRD) experiments failed. The mineral appears to be ductile; upon contact with a steel needle, it does not break but produces bent flakes. When subjected to XRD investigation, the results were invariably of poor quality, suggesting that scraping of the material deforms its internal structure.
In reflected light, zipserite has a greyish-white colour (Fig. 1a). Colour and reflectance are essentially indistinguishable from those of the host bismuthinite, making the mineral very difficult to differentiate from bismuthinite. Bireflectance is weak, with creamy white to grey–white colours. Zipserite has no pleochroism and moderately strong anisotropy. The colours of anisotropy are dark blue and grey (Fig. 1b). Zipserite has no internal reflections. Reflectance values (WTiC Zeiss 370) were measured in air (spectrophotometer MSP400 Tidas at Leica microscope, objective 20×). They are listed in Table 1 (COM standard wavelengths are given in bold) and shown in Fig. 2.
Table 1. Reflectance values for zipserite. The Committee on Ore Minerals (COM) standard wavelengths are given in bold.


Figure 2. Smoothed dispersion curves for zipserite. The reflectance values are listed in Table 1.
Chemical composition
Because of the differences in the average atomic number, zipserite can be much more easily differentiated from bismuthinite in back-scattered electron images (Fig. 1c). Quantitative chemical analyses (Table 2) on selected zipserite grains were carried out using a Jeol JXA 8530 electron microprobe (wavelength dispersive spectroscopy mode, 20 kV, 20 nA and 5 μm beam diameter, 20 s on the peak, 20 s on background) at the Department of Mineralogy at the Friedrich Schiller University in Jena. The estimated detection limits (in wt.%) were 0.01 for S, 0.03 for Fe and Cu, 0.06 for Sb, 0.07 for Se and Te, and 0.08 for Pb and Bi. Results (average of 10 spot analyses) are given in Table 2. Contents of other elements with atomic numbers >8 are below detection limits. Matrix correction by ZAF software was applied to the data. The empirical formula calculated on the basis of 9 apfu is (Bi4.74Pb0.31)Σ5.05(S3.38Se0.56Te0.02)Σ3.96, the idealised formula can be written as Bi5(S,Se)4. The ideal end-member formula of zipserite is Bi5S4, which requires Bi 89.07 and S 10.93, total 100 wt.%.
Table 2. Electron-microprobe analyses for zipserite. All data in wt.%.

S.D. – standard deviation
Crystal structure
As mentioned above, attempts to extract a grain for XRD analysis invariably failed. All the flakes extracted were unsuitable for structural characterisation. Therefore, we opted for the structure solution employing electron diffraction, which can easily collect data on a lamella at the nanoscale.
Slicing and polishing of a lamella for 3-dimensional electron diffraction analysis were carried out using a scanning electron microscope (SEM) coupled with a gallium-focused ion beam (FIB) source. The SEM–FIB (Helios G4 UX, ThermoFisherScientific) is equipped with a high-performance FIB source (Phoenix) that allows the polishing of transmission electron microscope (TEM) lamella at very low acceleration voltage or beam current. This feature is essential for obtaining undisturbed thin lamella suitable for high-resolution TEM imaging. Thin sections of samples, as used for optical-light microscopic investigation and other analyses, were sputtered with an ≈8 nm gold layer to ensure the electric conductivity of the full sample and to reduce sample abrasion during ion beam imaging. Sites for extraction of the lamellae were selected according to previous microscopic and spectroscopic characterisation of the samples. Areas of interest were covered with an ~ 15 × 15 × 3 μm layer of platinum to further protect the sample surface against ion beam damage.
The structure analyses were carried out at 98 K and at the ambient temperature (298 K) using the 3-dimensional electron diffraction (3D ED) technique (Gemmi and Lanza, Reference Gemmi and Lanza2019; Gemmi et al., Reference Gemmi, Mugnaioli, Gorelik, Kolb, Palatinus, Boullay, Hovmöller and Abrahams2019). The first data collection was carried out at low temperature to prevent beam-induced damage and to test the stability of the studied compound under the beam. The 3D ED data were collected on the thinnest part of the lamella (Fig. 3a), with a continuous rotation mode in a FEI Tecnai 02 transmission electron microscope (acceleration voltage of 200 kV, LaB6) equipped with a side-mounted hybrid single-electron detector ASI Cheetah M3, 512 × 512 pixels with high sensitivity and fast readout. A series of non-oriented patterns were collected continuously by steps of 0.25° (98 K) and 0.5° (298 K) on the accessible tilt range allowed by the preparation. The area of the lamella where data were collected is defined by the size of the 1 μm beam (nano diffraction mode) (Fig. 3b). Continuous-rotation 3D ED data (cRED) reduction was performed using the computer program PETS2 (Palatinus et al., Reference Palatinus, Brázda, Jelínek, Hrdá, Steciuk and Klementová2019; Brázda et al., Reference Brázda, Klementová, Krysiak and Palatinus2022). The specific data processing for cRED data used in the structure solution and the refinement is detailed extensively in Klar et al. (Reference Klar, Krysiak, Xu, Steciuk, Cho, Zou, Palatinus and Republic2023). It includes overlapping virtual frames (OVFs) for the dynamical refinement that aims to model experimental intensities from continuous rotation data by summing consecutive experimental diffraction patterns into a set of virtual frames (see experimental details in Table 3). Data collected on zipserite show very broad reflections for both temperatures. It leads to very high values of Rocking curve width = 0.0065 Å–1 (98 K), and 0.007 Å–1 (298 K), and apparent mosaicity = 1.167° (98 K) and 1° (298 K), which affects the accuracy of the refined model (Fig. 4). The data reduction for the structure solution leads to an hkl-type file with Rint(obs/all) = 0.1370/0.1370 and 81.91% coverage, and Rint(obs/all) = 0.2082/0.2086 and 91.58% coverage for sinθ/λ = 0.7Å–1 (Laue class $\bar{3}$![]() m) for the data collected at 98 K and 298 K, respectively. For the dynamical refinement, another hkl-type file is generated where each OVF is independently refined (Palatinus et al., Reference Palatinus, Corrêa, Steciuk, Jacob, Roussel, Boullay, Klementová, Gemmi, Kopeček, Domeneghetti, Cámara and Petříček2015a, Reference Palatinus, Petříček and Correâ2015b; Klar et al., Reference Klar, Krysiak, Xu, Steciuk, Cho, Zou, Palatinus and Republic2023). The structure was solved using Superflip (Palatinus and Chapuis, Reference Palatinus and Chapuis2007; Palatinus, Reference Palatinus2013) in Jana2020 (Petříček et al., Reference Petříček, Palatinus, Plášil and Dušek2023) and refined using DYNGO and Jana2020 (Petříček et al., Reference Petříček, Palatinus, Plášil and Dušek2023).
m) for the data collected at 98 K and 298 K, respectively. For the dynamical refinement, another hkl-type file is generated where each OVF is independently refined (Palatinus et al., Reference Palatinus, Corrêa, Steciuk, Jacob, Roussel, Boullay, Klementová, Gemmi, Kopeček, Domeneghetti, Cámara and Petříček2015a, Reference Palatinus, Petříček and Correâ2015b; Klar et al., Reference Klar, Krysiak, Xu, Steciuk, Cho, Zou, Palatinus and Republic2023). The structure was solved using Superflip (Palatinus and Chapuis, Reference Palatinus and Chapuis2007; Palatinus, Reference Palatinus2013) in Jana2020 (Petříček et al., Reference Petříček, Palatinus, Plášil and Dušek2023) and refined using DYNGO and Jana2020 (Petříček et al., Reference Petříček, Palatinus, Plášil and Dušek2023).

Figure 3. (a) SEM image of the lamella prepared from the Bi5(S,Se)4 phase. (b) TEM picture of lamellae and the area selected (red circle) for the 3D ED data collection at 98 K.
Table 3. cRED data collection and structure refinement details for Bi5(S,Se)4.


Figure 4. Plots of the rocking-curve profiles (Camel plot) of the experimental 3D ED data at 98 K and 298 K. The lowest blue curve is the averaged observed rocking curve in the range of 0.2 to 0.3 Å−1 and the next ones are obtained by steps of 0.1 Å−1. The red curves are the calculated ones from the three parameters Rocking curve width, apparent mosaicity and tilt semi-angle angle. Reflections are involved in the Camel plot for I > 10σ(I).
At 98 K, the structure is described using the superspace formalism with a R-centred trigonal unit cell of a = 4.209(2) Å and c 0 = 5.616(6) Å, a modulation vector q ≈ 4/3 c* and, the superspace group R $\bar{3}$![]() m(00γ)00 (R obs with –h+k+l+m = 3n) (Fig. 5). Satellite reflections are visible up to the second order (Fig. 5a,c). At 98 K and 298 K, the component of the modulation wave vector appears very close to a commensurate value. The choice of the superspace formalism over a 3-dimensional cell with 3c 0 (P $\bar{3}$
m(00γ)00 (R obs with –h+k+l+m = 3n) (Fig. 5). Satellite reflections are visible up to the second order (Fig. 5a,c). At 98 K and 298 K, the component of the modulation wave vector appears very close to a commensurate value. The choice of the superspace formalism over a 3-dimensional cell with 3c 0 (P $\bar{3}$![]() m) was made because of the intensity repartition, and the possibility of more accurately describing the ordering between Bi and S/Se atoms. The second-order satellite reflections were involved in the structure solution but must be discarded from the refinement as their integration was found to be inaccurate (Fig. S1). The recent ‘fit profile’ option in PETS2 allows better integration of close reflections. However, for zipserite, the c-axis, where the modulation takes place, is lying along the beam direction during the experiment and is associated with an unusually high mosaicity.
m) was made because of the intensity repartition, and the possibility of more accurately describing the ordering between Bi and S/Se atoms. The second-order satellite reflections were involved in the structure solution but must be discarded from the refinement as their integration was found to be inaccurate (Fig. S1). The recent ‘fit profile’ option in PETS2 allows better integration of close reflections. However, for zipserite, the c-axis, where the modulation takes place, is lying along the beam direction during the experiment and is associated with an unusually high mosaicity.

Figure 5. Indexing using the superspace (SS) formalism a = 4.209(2), c = 5.610(6) Å, q = 1.325(5)c* and R $\bar{3}$![]() m(00γ)00 and represented in (a) one folded unit cell, and (b) in an extended unit cell 3a*3a*3c* where the R centring is visible for main (blue) and the satellite (red) reflections (PETS2 software). (c) Sections hk0m and 0klm of the reciprocal space highlighting a few main (blue), first order satellite (pink), and second order (yellow) satellite reflections.
m(00γ)00 and represented in (a) one folded unit cell, and (b) in an extended unit cell 3a*3a*3c* where the R centring is visible for main (blue) and the satellite (red) reflections (PETS2 software). (c) Sections hk0m and 0klm of the reciprocal space highlighting a few main (blue), first order satellite (pink), and second order (yellow) satellite reflections.
The result of the charge flipping algorithm (Superflip) is a (3+1)-dimensional map of the electrostatic potential (emap) that is interpreted according to the isosurface levels (V(r)). The initial model has only 1 independent atomic site. The repartition of the electrostatic potential on this site along the modulation axis x4 can be visualised on de-Wolf sections x1–x4 and x3–x4 (Fig. 6a). The model was further elaborated by splitting the domain in two using crenel functions to describe the occupational modulation between Bi and S/Se, and Legendre polynomials in crenel intervals to account for a possible positional modulation. The ordering is considered between Bi and S/Se. From the quality of the present data set, we cannot speculate on a possible additional ordering between S and Se. The first atomic site is defined with a crenel function for Bi as x 04 = 0.5, the centre of the crenel and Δ[Bi] = 5/9 ≈ 0.556, the width of the domain according to the chemical composition. The S/Se domain is then defined with x 04 = 0 and Δ[S/Se] = 1–5/9 = 4/9 ≈ 0.444. The amount of S and Se on this domain is set to agree with the result of the chemical analysis as S:Se = 85:15. The same model was obtained for the 3D ED data collected at 98 K and 298 K (Table 3). The refinements were carried out using both the kinematical and the dynamical approaches (Table 3). Imperfect crystals tend to diffract more kinematically which usually results in a smaller decrease of the R-factors from the kinematical to the dynamical refinement, as is the case here. However, it does not mean that the multiple scattering does not occur (dynamical diffraction), especially when heavy atoms are involved. Due to data limitations, i.e. strong mosaicity, absence of the second order in the refinement and lower data coverage along c, the refinements were performed using restrictions on the distances between Bi and S/Se. The displacive modulation appears correlated to the anisotropic displacement along c. Therefore, gentle restrictions allowed more meaningful Bi–(S/Se) distances, compared with the values found in the literature. The refinement using the dynamical and the kinematical approaches led to very close results in terms of displacement parameters. The results of the dynamical refinement are nevertheless preferred as the R values improved and this refinement was performed on more reflections (Palatinus et al., Reference Palatinus, Corrêa, Steciuk, Jacob, Roussel, Boullay, Klementová, Gemmi, Kopeček, Domeneghetti, Cámara and Petříček2015a, Reference Palatinus, Petříček and Correâ2015b; Klar et al., Reference Klar, Krysiak, Xu, Steciuk, Cho, Zou, Palatinus and Republic2023). At 98 K, the refinement converged to R(obs)/wR(obs) = 0.096/0.1185 and R(all)/wR(all) = 0.096/0.1185 for 768 observed reflections and 60 refined parameters including only six structural ones. At 298 K, the results are R(obs)/wR(obs) = 0.1142/0.1376, R(all)/wR(all) = 0.1192/0.1380 for 616 observed reflections and 47 refined parameters for six structural ones. The detail of the R values for the main and satellite reflections is given in Table 3. For Z = 1, the general formula is Bi1.667(S1.133Se0.2)Σ1.333 corresponding to x = 0.556 when the formula is expressed as Bix(S,Se)1–x. The Bi–Bi and Bi–S/Se distances along the parameter t at 98 K and 298 K are presented in Fig. 6b, the positional parameters and atomic displacement parameters in Tables 4 and 5, respectively. The parameter t is defined as x̄(s,4) = t + q⋅x̄(u), 0 < t < 1. By construction, the fourth coordinate axis in superspace is perpendicular to physical space. The fourth coordinate x̄(s,4) of a point in superspace then is x̄(s,4) = t + q⋅x̄(u), where x̄(u) are the three coordinates of atom u in the basic (average) structure. The parameter t can be considered as the initial phase of the modulation wave. Different values of t give shifted, but entirely equivalent representations of physical space. For crystal structures, the variation of environments of a particular atom of the basic structure can be obtained as a function of t of structural parameters, like atomic displacements, atomic distances, bond angles, etc. The structure is shown in Fig. 7.

Figure 6. (a) De Wolf sections x1–x4 and x3–x4 drawn from F(obs) with Bi and S/Se domains along x4 using crenel functions and Legendre polynomials in crenel intervals (98 K). (b) Distances Bi–Bi and Bi–S/Se along the parameter t at 98 K and 298 K. This parameter is explained in detail in the text.
Table 4. Positional parameters and atomic displacement parameters for the crystal structure of zipserite at 298 K.

Table 5. Positional parameters and atomic displacement parameters for the crystal structure of zipserite at 98 K.


Figure 7. (a) Crystal structure of Bi5S4 (i.e. no Se considered as it is a minor element in the structure with no separate positions) represented in the supercell a × b × 3c 0 (space group P $\bar{3}$![]() m1). (b) Bi5S4 represented in an extended supercell to show the stacking of Bi2 and Bi3S4 layers. Drawn using CrystalMaker® software.
m1). (b) Bi5S4 represented in an extended supercell to show the stacking of Bi2 and Bi3S4 layers. Drawn using CrystalMaker® software.
Powder XRD data of zipserite could not be collected, due to the paucity of available material. Consequently, powder XRD data, given in Table 6, were calculated using the software PowderCell 2.3 (Kraus and Nolze, Reference Kraus and Nolze1996) on the basis of the structural model given in Table 4. The crystallographic information files have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary material (see below).
Table 6. Calculated powder XRD data for zipserite.*

* Intensity and d hkl were calculated using the software PowderCell2.3 (Kraus and Nolze, Reference Kraus and Nolze1996) on the basis of the structural model given in Tables 3 and 4. Only reflections with I calc > 2 are listed. The five strongest reflections are given in bold.
Discussion
An easier way to visualise the structure is to draw the model in the closest supercell a × b × 3c 0 with formula Bi5(S3.4Se0.6)Σ4 (space group P $\bar{3}$![]() m) (Fig. 7). Bi5(S3.4Se0.6)Σ4 is built from the alternation of the double bismuth layer Bi2 and the Bi3S4 block which is a three BiS6 octahedra thick layer. Its general formula can be expressed as Bi2 + Bi3S4, which corresponds directly to the observed stacking. For both temperatures, the Bi–Bi distances are constant along the modulation with Bi–Bi = 3.118(7) Å at 98 K, and Bi–Bi = 3.221(11) Å at 298 K and correspond to the double bismuth layer. In the Bi3S4 block, bismuth atoms are not located at the centre of the octahedra formed by neighbouring S/Se atoms. The refined positional modulation parameter for bismuth (zort1) is almost zero whereas the values go up to 0.109(8) for S/Se at 98 K and 0.0745(11) at 298 K. This is illustrated by the variation of Bi–S/Se distances along the domain which is only due to a significant displacement of S/Se along c (Fig. 6b). The longest Bi–S/Se distances are found between the Bi2 double layer, and the first S/Se positions. This result is totally consistent with what is observed in the (Bi2)m(Bi2Te3)n system (Bos et al., Reference Bos, Faucheux, Downie and Marcinkova2012). The temperature induces a difference in the modulation amplitudes, where lower temperature data show a stronger evolution of the Bi–S/Se distances (from 2.76 (3) Å to 3.43(3) Å at 98 K, and from 2.95(4) Å to 3.42(4) Å at 298 K). Note that the difference observed for the modulation parameters might be a bit inflated by the lower coverage of the data at 98 K (81.92%) as compared to the data collected at the ambient temperature. Nevertheless, the Bi atoms, being part of the Bi3S4 blocks, are shifted significantly from the exact central position defined by the surrounding S/Se atoms. Such a feature has already been observed for compounds of the same family (Fig. 8). This scheme only includes binary compounds, but many more doped materials exist (Aliev et al., Reference Aliev, Amiraslanov, Nasonova, Shevelkov, Abdullayev, Jahangirli, Orujlu, Otrokov, Mamedov, Babanly and Chulkov2019), allowing more complex stackings. Bos et al. (Reference Bos, Faucheux, Downie and Marcinkova2012) described the structure and the properties of the (Bi2)m(Bi2Te3)n natural superlattices synthesised with compositions BixTe1–x with 0.44≤ x ≤0.70. They found an infinitely adaptive series of layered (Bi2)m and (Bi2Te3)n (2-octahedra thick) natural superlattices consisting of different stacking sequences of Bi double layers and Bi2Te3 blocks. In Fig. 8, several examples of fully ordered and disordered structures are shown. The stacking of all ordered structures can be derived through their composition by decomposing the nominal composition into not only (Bi2)m and (Bi2Te3)n but a flexible combination of (Bi2)m, (BiTe2)n, (Bi2Te3)o, (Bi3Te4)p, and so on (see the insert in Fig. 8). BiSe stacking can be determined as [2*Bi2S3 + Bi2] (Gardes et al., Reference Gardes, Brun and Tedenac1989). In the system Bi–Te for x = 2/3 and (Bi2Te3)n for x = 0.7, the structures are disordered (Glazov et al., Reference Glazov1984; Yamana et al., Reference Yamana, Kihara and Matsumoto1979) as their formula cannot be decomposed into a series of basic structural units. Moreover, the refinement of zipserite in the commensurate option did not lead to good results. It suggests that the component of modulation wave vector is not exactly 4/3 for x = 0.556 and can probably evolve with the composition. We can presume that zipserite can show some structural flexibility to accommodate chemical variations (particularly S/Se ratio) depending on the available elements in the geological environment. It could be present under a slightly different combination of (Bi2)m and (Bi3S4)p, maybe as even more complex, uneven stacking of blocks [(Bi2S3)o + (Bi4S5)q] such as for systems where Bi is doped with other elements like MnBi4Te4 or MnBi6Te10 (Aliev et al., Reference Aliev, Amiraslanov, Nasonova, Shevelkov, Abdullayev, Jahangirli, Orujlu, Otrokov, Mamedov, Babanly and Chulkov2019).
m) (Fig. 7). Bi5(S3.4Se0.6)Σ4 is built from the alternation of the double bismuth layer Bi2 and the Bi3S4 block which is a three BiS6 octahedra thick layer. Its general formula can be expressed as Bi2 + Bi3S4, which corresponds directly to the observed stacking. For both temperatures, the Bi–Bi distances are constant along the modulation with Bi–Bi = 3.118(7) Å at 98 K, and Bi–Bi = 3.221(11) Å at 298 K and correspond to the double bismuth layer. In the Bi3S4 block, bismuth atoms are not located at the centre of the octahedra formed by neighbouring S/Se atoms. The refined positional modulation parameter for bismuth (zort1) is almost zero whereas the values go up to 0.109(8) for S/Se at 98 K and 0.0745(11) at 298 K. This is illustrated by the variation of Bi–S/Se distances along the domain which is only due to a significant displacement of S/Se along c (Fig. 6b). The longest Bi–S/Se distances are found between the Bi2 double layer, and the first S/Se positions. This result is totally consistent with what is observed in the (Bi2)m(Bi2Te3)n system (Bos et al., Reference Bos, Faucheux, Downie and Marcinkova2012). The temperature induces a difference in the modulation amplitudes, where lower temperature data show a stronger evolution of the Bi–S/Se distances (from 2.76 (3) Å to 3.43(3) Å at 98 K, and from 2.95(4) Å to 3.42(4) Å at 298 K). Note that the difference observed for the modulation parameters might be a bit inflated by the lower coverage of the data at 98 K (81.92%) as compared to the data collected at the ambient temperature. Nevertheless, the Bi atoms, being part of the Bi3S4 blocks, are shifted significantly from the exact central position defined by the surrounding S/Se atoms. Such a feature has already been observed for compounds of the same family (Fig. 8). This scheme only includes binary compounds, but many more doped materials exist (Aliev et al., Reference Aliev, Amiraslanov, Nasonova, Shevelkov, Abdullayev, Jahangirli, Orujlu, Otrokov, Mamedov, Babanly and Chulkov2019), allowing more complex stackings. Bos et al. (Reference Bos, Faucheux, Downie and Marcinkova2012) described the structure and the properties of the (Bi2)m(Bi2Te3)n natural superlattices synthesised with compositions BixTe1–x with 0.44≤ x ≤0.70. They found an infinitely adaptive series of layered (Bi2)m and (Bi2Te3)n (2-octahedra thick) natural superlattices consisting of different stacking sequences of Bi double layers and Bi2Te3 blocks. In Fig. 8, several examples of fully ordered and disordered structures are shown. The stacking of all ordered structures can be derived through their composition by decomposing the nominal composition into not only (Bi2)m and (Bi2Te3)n but a flexible combination of (Bi2)m, (BiTe2)n, (Bi2Te3)o, (Bi3Te4)p, and so on (see the insert in Fig. 8). BiSe stacking can be determined as [2*Bi2S3 + Bi2] (Gardes et al., Reference Gardes, Brun and Tedenac1989). In the system Bi–Te for x = 2/3 and (Bi2Te3)n for x = 0.7, the structures are disordered (Glazov et al., Reference Glazov1984; Yamana et al., Reference Yamana, Kihara and Matsumoto1979) as their formula cannot be decomposed into a series of basic structural units. Moreover, the refinement of zipserite in the commensurate option did not lead to good results. It suggests that the component of modulation wave vector is not exactly 4/3 for x = 0.556 and can probably evolve with the composition. We can presume that zipserite can show some structural flexibility to accommodate chemical variations (particularly S/Se ratio) depending on the available elements in the geological environment. It could be present under a slightly different combination of (Bi2)m and (Bi3S4)p, maybe as even more complex, uneven stacking of blocks [(Bi2S3)o + (Bi4S5)q] such as for systems where Bi is doped with other elements like MnBi4Te4 or MnBi6Te10 (Aliev et al., Reference Aliev, Amiraslanov, Nasonova, Shevelkov, Abdullayev, Jahangirli, Orujlu, Otrokov, Mamedov, Babanly and Chulkov2019).

Figure 8. Scheme with related synthetic compounds sorted by their x ratio. References: [1] Nakajima (Reference Nakajima1963); [2] Gardes et al. (Reference Gardes, Brun and Tedenac1989); [3] Yamana et al. (Reference Yamana, Kihara and Matsumoto1979); [4] Glazov (Reference Glazov1984); [5] Semiletov and Pinsker (Reference Semiletov and Pinsker1955). The basic structural units are presented in the insert.
Following the results of the crystal structure analysis of zipserite (occupation of 2c site Se0.41S0.35Bi0.24), its ideal formula could be written as Bi5S2Se2 (Nickel and Grice, Reference Nickel and Grice1998). However, difficulties related to the refinement of the zipserite structure and the measured (using electron probe microanalysis) Se contents of only 0.56 apfu leave some questions regarding the exact composition open. For nomenclature purposes, we propose that the 2c and 2d sites should be considered as an aggregate site, avoiding the creation of different isotypes of zipserite based on different S/Se ratios. Thus, species with S > Se should be classified as zipserite, and those with Se > S could be described as a potential new mineral species.
Conclusions
Zipserite is a new phase in the Bi–S(–Se) system related to the tetradymite archetype (Cook et al., Reference Cook, Ciobanu, Wagner and Stanley2007) and it does not correspond to any valid or invalid unnamed mineral of Smith and Nickel (Reference Smith and Nickel2007). Its discovery and comparison with previously known Bi chalcogenides confirm the fundamental role of studies devoted to natural mineral assemblages to reveal novel crystal structures so far not synthesised in a laboratory (e.g. Gardes et al., Reference Gardes, Brun and Tedenac1989; Lin et al., Reference Lin, Sharma and Chang1996; Kitakaze, Reference Kitakaze2016, Reference Kitakaze2017; Bindi et al., Reference Bindi, Nespolo, Krivovichev, Chapuis and Biagioni2020).
Acknowledgements
We appreciate the constructive comments of three anonymous reviewers and the editorial handling by Owen Missen. GS wants to thank Lukáš Palatinus for the extra brain cells as well the CzechNanoLab project LM2023051 funded by MEYS CR for the financial support of the measurements/sample fabrication at LNSM Research Infrastructure. This work is also supported by the Czech Science Foundation, project number 21-05926X. JS acknowledges financial support by the Ministry of Culture of the Czech Republic (long-term project DKRVO 2024–2028/1.II.a; National Museum, 00023272).
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1180/mgm.2024.37.
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.