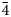Introduction
Theuerdankite, ideally Ag3AsO4, is a new silver mineral from the famous historic mining region of St. Andreasberg in Lower Saxony, Germany. It is named after the type locality, the Alter Theuerdank Mine. The new mineral and its name (symbol Td) have been approved by the Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2023–009, Plášil et al., Reference Plášil, Sejkora, Dolníček, Désor, Gross and Möhn2023). The holotype specimen (polished section) of theuerdankite is deposited in the collections of the Department of Mineralogy and Petrology, National Museum in Prague, Cirkusová 1740, 193 00 Prague 9, Czech Republic under the catalogue number P1P 59/2022. Here, we report on its description, including crystal structure refinement using a Gram–Charlier development describing the thermal movement of the silver atom in the crystal structure, which vibrates anharmonically around its equilibrium position. We also append a discussion on the proper handling of the diffraction data and the refinement.
Occurrence
Theuerdankite was found on a single specimen originating from the Alter Theuerdank Mine, Beerberg, St Andreasberg, Braunlage, Goslar District, Lower Saxony, Germany (51°42' 29''N, 10°31'41''E). This mine is among the important mines in the St. Andreasberg mining district and it is famous for the rich findings of the so-called ‘buttermilch-erz’ = ore consisting of chlorargyrite. We refer to the paper by Schnorrer et al. (Reference Schnorrer, Kronz, Liesmann and Kehr2009) for details on the occurrence and geology. Associated minerals within the specimen studied are chlorargyrite, native silver and calcite. Theuerdankite is most probably of supergene origin but could also be late hydrothermal if these fluids were oxidising enough to convert As in the primary minerals to arsenates.
Physical and optical properties
Theuerdankite occurs as irregular aggregates up to 3 mm in size (Fig. 1), growing in cavities of strongly supergene-weathered material consisting of native silver and chlorargyrite. Its colour is dark violet, changing to reddish and black when exposed to the air. It darkens when exposed to light. It has a grey to violet grey streak; when fresh, its streak is brownish-red. It is non-fluorescent in SW and LW ultraviolet light. The Mohs hardness is estimated at ~2 based on scratch tests. Theuerdankite is brittle; no cleavage and no parting were observed. The fracture is conchoidal. The calculated density (Z = 2), based on the empirical formula and the unit-cell parameters refined from single-crystal X-ray diffraction data, is 6.620 g⋅cm–3. Theuerdankite is dark grey with pinkish tints in reflected light with no visible bireflectance and no pleochroism; no anisotropy has been observed. There are dark red internal reflections, visible around fractures, and inclusions of native silver (Fig. 2). Reflectance values measured in air using a spectrophotometer MSP400 Tidas at Leica microscope, with a 20× objective, are given in Table 1 and shown in Fig. 3.

Figure 1. Theuerdankite (1) from the type locality associated with native silver (2) and chlorargyrite (3) in the cavity of strongly supergene-weathered material; Field of view: 3.6 mm; holotype specimen (P1P 59/2022); photo M. Gross.

Figure 2. Dark-red internal reflections in theuerdankite visible especially around fractures and inclusions of native silver (white); field of view: 700 μm; photo in reflected light (partly crossed polars) by J. Sejkora.
Table 1. Reflectance data for theuerdankite*.

* The reference wavelengths required by the Commission on Ore Mineralogy (COM) are given in bold.

Figure 3. Reflectivity curve for theuerdankite from the Alter Theuerdank Mine, St Andreasberg, Germany.
Chemical composition
Quantitative chemical analyses were carried out using a Cameca SX100 electron microprobe (WDS mode, 15 kV, 5 nA and 10 μm beam diameter) at the National Museum Prague, Czech Republic. The following standards and X-ray lines were used to minimise line overlaps: Ag (AgLα), chalcopyrite (CuKα), clinoclase (AsLα) and fluorapatite (PKα). Peak counting times were 20 s for all elements and 10 s for each background. The results obtained (average of 16 spot analyses) are given in Table 2. Contents of other elements with atomic numbers higher than that of C (Z = 6) are below detection limits. Matrix correction by PAP software (Pouchou and Pichoir, Reference Pouchou, Pichoir and Armstrong1985) was applied to the data. The calculated empirical formula of theuerdankite based on 4 atoms per formula unit and 4 O atoms is Ag3.00As1.00O4. The ideal formula for theuerdankite is Ag3AsO4, which requires Ag2O 75.15 and As2O5 24.85, a total of 100.00 wt.%. It is soluble in a 25% ammonia solution and decomposes when heated up in a melting point tube without the evolution of H2O.
Table 2. Chemical composition (n = 12) (in wt.%) of theuerdankite.

S.D. – standard deviation
Raman spectroscopy
The Raman spectra of theuerdankite were collected in the range 50–4000 cm–1 using a DXR dispersive Raman Spectrometer (Thermo Scientific) mounted on a confocal Olympus microscope. The Raman signal was excited by an unpolarised green 532 nm solid state, diode-pumped laser and detected by a CCD detector. The experimental parameters were: 100× objective, 10 s exposure time, 100 exposures, 50 μm slit spectrograph aperture and 1 mW laser power level. The eventual thermal damage of the measured points was excluded by visual inspection of the excited surface after measurement, observation of possible decay of spectral features at the start of excitation, and checking for a thermal downshift of Raman lines. The instrument was set up using a software-controlled calibration procedure using multiple neon emission lines (wavelength calibration), multiple polystyrene Raman bands (laser frequency calibration), and standardised white-light sources (intensity calibration). Spectral manipulations were performed using the Omnic 9 software (Thermo Scientific).
The Raman spectrum of theuerdankite is given in Fig. 4. The main bands observed are (in wavenumbers): 816, 787, 408, 337 and 82 cm–1. The most prominent very strong Raman band at 787 cm–1 with a shoulder at 816 cm–1 is attributed to overlapping ν1 (AsO4)3– symmetric stretching and ν3 (AsO4)3– antisymmetric stretching vibrations. The Raman band at 408 cm–1 is attributed to the ν4 (AsO4)3– bending vibration. The Raman band at 337 cm–1 is related to the ν2 (AsO4)3– bending vibrations and those below 200 cm–1 to lattice modes (Vansant et al., Reference Vansant, van Der Veken and Desseyn1973; Nakamoto, Reference Nakamoto2009; Frost et al., Reference Frost, Čejka, Sejkora, Plášil, Bahfenne and Palmer2010; Čejka et al., Reference Čejka, Sejkora, Bahfenne, Palmer, Plášil and Frost2011). The observed bands are comparable to those in the infrared absorption spectrum of the synthetic Ag3AsO4 — 825, 785, 405 and 330 cm–1 (Hájek et al., Reference Hájek, Muck and Smrčková1979; Muck et al., Reference Muck1980).

Figure 4. Raman spectrum of theuerdankite.
X-ray crystallography and structure refinement
Powder X-ray diffraction (XRD) data of theuerdankite were obtained using a pseudo-Gandolfi scan on a XtaLAB Synergy R, DW system equipped with the HyPix-Arc150 detector, using monochromatic MoKα radiation from the microfocus rotating anode. The positions and intensities of the diffraction peaks were found and refined using the Pearson VII profile-shape function of the ZDS program package (Ondruš, Reference Ondruš1993). The unit-cell parameters were refined by the least-squares program of Burnham (Reference Burnham1962). The powder X-ray diffraction data of theuerdankite are given in Table 3. The refined unit-cell parameter (for the space group P $\bar{4}$![]() 3n) is a = 6.1448(3) Å, with V = 231.01(2) Å3 and Z = 2.
3n) is a = 6.1448(3) Å, with V = 231.01(2) Å3 and Z = 2.
Table 3. Powder X-ray diffraction data (d in Å) for theuerdankite; the six strongest diffractions are reported in bold.

*Icalc.; *dcalc. – Intensity and d hkl (in Å) calculated using the software PowderCell2.3 (Kraus and Nolze, Reference Hájek, Muck and Smrčková1996) on the basis of the structural model given in Tables 4 and 5. Only reflections with I calc > 0.5 are listed.
Table 4. Summary of data collection and refinements (harmonic/anharmonic) for theuerdankite.

Table 5. Atom positions, equivalent displacement parameters (in Å2) and bond-valence sums (BVS; in valence units) for theuerdankite.

Single-crystal XRD data for theuerdankite were collected on an XtaLAB Synergy, DW system equipped with the HyPix-Arc150 detector, using monochromatic MoKα radiation from the microfocus rotating anode from the same crystal as powder XRD data were collected. A fragment of the single crystal with approximate dimensions 85 × 48 × 28 μm was mounted on a glass fibre and analysed. The complete data set (100% to the resolution of 0.4 Å) of the high-redundancy (>6) was collected using ω-scans (frame width of 0.5° and a counting time of 4 seconds per frame). Data reduction was performed using CrysAlisPro Version 1.171.43.111 (Rigaku, 2024). The data were corrected for Lorentz factor and absorption (multi-scan, ABSPACK scaling algorithm; Rigaku, 2024).
The structure of theuerdankite was solved from the intensity data using the intrinsic phasing by the SHELXT program (Sheldrick, Reference Sheldrick2015) and refined using the software Jana2020 (Petříček et al., Reference Petříček, Palatinus, Plášil and Dušek2023). The structure was refined as an inversion twin, and extinction (isotropic; Becker and Coppens, Reference Becker and Coppens1974) was also refined during the final stages of the refinement (Table 4). We used a Wilson modification to the least-square routine (weights) to avoid the statistical bias (Wilson, Reference Wilson1976). We employed the third-order anharmonic Gram–Charlier development (see for instance Volkov et al., Reference Volkov, Charkin, Firsova, Aksenov and Bubnova2023) to describe the Debye–Waller factors for the Ag atoms, which improved the refinement considerably (see the Discussion). Refinement details are given in Table 4, atomic parameters (including atomic displacement parameters (ADP) and bond-valence sums calculated using parameters reported by Gagné and Hawthorne, Reference Gagné and Hawthorne2015) are given in Table 5 and Table 6; the coefficients of the third-order Gram–Charlier development are given in the Supplementary crystallographic information file (cif, see below); selected interatomic distances are reported in Table 7. The Vesta program (Momma and Izumi, Reference Momma and Izumi2011) was used to plot the electron density and the isosurface for ADPs of silver atoms.
Table 6. Anisotropic displacement parameters (in Å2) for atoms in the theuerdankite structure.

Table 7. Selected interatomic distances (in Å) in theuerdankite.

The structure of theuerdankite contains AsO4 tetrahedra (Table 5) whose centres lie on lattice points of a b.c.c. lattice. The Ag1 atom occupies the 6c Wyckoff position, surrounded by four O atoms at a distance of 2.372(2) Å. The displacement of the Ag atom is slightly anisotropic with the general direction of vibration perpendicular to a plane formed approximately by four symmetrically related O1 atoms and assumes a pear-like shape (Fig. 6).
Related minerals and structures
The structure of theuerdankite is isotypic to that of synthetic Ag3PO4 (Ng et al., Reference Ng, Calvo and Faggiani1978) and synthetic Ag3AsO4 (Weil, Reference Weil2003). The electronic structure of the synthetic analogue of theuerdankite has been investigated (e.g. Reunchan et al., Reference Reunchan, Boonchun and Umezawa2016; Li and Chen, Reference Li and Chen2017) due to its promising photocatalytic properties.
As a chemically related mineral, tetragonal tillmannsite, (Ag3Hg)(V,As)O4 (Sarp et al., Reference Sarp, Pushcharovsky, MacLean, Teat and Zubkova2003) could be considered. However, theuerdankite is structurally wholly distinctive. Tillmannsite contains isolated (V,As)O4 tetrahedra and (Ag3Hg) tetrahedral clusters. Clusters are specific for the disordered distribution of Ag and Hg atoms, which is a distinctive feature over chemically related synthetic compounds AgHg2PO4 and AgHg2AsO4 (Masse et al., Reference Masse, Guitel and Durif1978) where Ag and Hg atoms are completely ordered and form the dimers O2Ag–AgO2 and O3Hg–HgO3. In tillmannsite, each (Ag,Hg) metallic atom is coordinated by three metallic neighbours and by three oxygens.
Also, cubic rudabányaite, (Ag2Hg2)(AsO4)Cl (Effenberger et al., Reference Effenberger, Szakall, Feher, Vaczi and Zajzon2019) can be viewed as a related mineral species but is structurally completely different. Its crystal structure is a framework based on by two crystallographically different [M 4]4+ cluster cations forming tetrahedra (M = (Ag,Hg) with a ratio Ag:Hg ~ 1:1), with no evidence for ordering between the Ag and Hg atoms. Small amounts of the M atoms are displaced by ~0.5 Å. Topologically, the barycentres of the [M 4]4+ clusters and the As atom positions of the crystal structure of rudabányaite form a cubic primitive lattice with a’ = 1/2a = 8.68 Å; half of the voids are occupied by Cl atoms.
Discussion
Harmonic vs. anharmonic refinement and adequate data handling
Initially, the structure of theuerdankite was refined using a harmonic approach to the displacement parameters of all atoms, thus described by the thermal ellipsoids. The final refinement converged smoothly (including isotropic extinction and inversion twin) to somewhat acceptable R-factors (comparison of harmonic and anharmonic refinement given in Table 4). However, one may suggest that the goodness-of-fit (GoF) from the harmonic refinement (GoF = 2.83 for all reflections) is rather high for a correct model and a reliable refinement. Nevertheless, these issues warrant further discussion. The standard approach to the goodness-of-fit and, consequently, a weighting scheme for the refinement is somewhat misleadingly applied by many users. The most widely used program for the structure refinement from the single-crystal X-ray data, SHELXL (Sheldrick, Reference Sheldrick2008), forces (if not changed by the user) the refinement to achieve a GoF value close to unity, namely by changing (refining) the weights. In contrast to this approach, the program Jana2020 (Petříček et al., Reference Petříček, Palatinus, Plášil and Dušek2023) does not refine the weighting scheme but bases it purely on the experimental expectations (see _refine_ls_weighting_details in the cif) that does not force GoF to be one. Therefore, in general, the GoF values obtained by Jana are usually larger than most of those reported by the SHELX program. The GoF values in Jana, however, do have a physical meaning. For example, if the final reported GoF is >2.0, it does not automatically mean that the model is incorrect or entirely wrong. It just means that there are some features within a given dataset that the current model 1) does not describe/fit data well enough, or 2) there are systematic errors inherent to the diffraction data (from the measurement, for instance). Such undescribed features can include disorder (both positional or occupational), hidden twinning, modulation, or deformation of electron density (charge-density studies). Therefore, this approach also requires a careful and meaningful handling and evaluation of the diffraction data. In Jana, there are several ways of data handling, including different schemes and approaches to averaging the reflection file for refinement (for details, see Petříček et al., Reference Petříček, Dušek and Palatinus2014, Reference Petříček, Palatinus, Plášil and Dušek2023). Here, we used the refinement file obtained by averaging measured reflections using Poisson statistics. We used a refined instability factor value (= 0.010409), close to the most typical value of instability factor tested over the years of the Jana program development, which is 0.01 for the ‘non problematic’ datasets. The actual value of the instability factor for the given diffraction dataset is deduced during the merging of reflections. The instability factor corrects the sigma values of individual/merged reflections obtained from the experimental reflection file provided by the diffractometer/data reduction program, such as they are fitted to the values obtained from merging statistics (Poisson). We recommend using the refined value of the instability factor for highly redundant datasets with expected reliable merging statistics. For comparison, we present here difference-Fourier maps obtained from the harmonic refinements with different weights (Fig. 5a–c). It is apparent how the choice of the ‘proper’ weights affects the results of the refinement (and in the worst case, the wrong choice of the weights can lead to biased refinement and interpretation). Finally, we relied on a refined value of the instability factor (corresponding map displayed in Fig. 5b) and used it for the final refinement of the structure with an anharmonic approach to the atomic displacement parameters of silver (using a Gram–Charlier development). The final refinement converged to R 1 = 1.69% for 519 observed reflections and GoF of 1.54. The final difference-Fourier map is provided in Fig. 6a; the highest residual density is located around the silver atom (Fig. 6b). For comparison, the refinement with instability coefficient = 0.08 (overestimated!) would lead, in the case of anharmonic refinement, to R 1 = 2.31% for 519 observed reflections and a (alarming!) goodness-of-fit = 0.76 with corresponding difference-Fourier electron density of 0.56 and –0.6 e–/Å3.

Figure 5. Difference-Fourier maps from the crystal structure refinements of theuerdankite using distinct weights (given) and harmonic approach to the ADP of silver. Colour scheme: Ag = pale blue, As = green, O = red; solid lines = positive contours, dashed lines = negative contours; numbers (pale blue) = highest electron density (e –/Å3). (a) Refinement relying on statistics only returned a rather ‘noisy’ difference map with too many features. (b) Refinement using a refined value of the instability factor provides a less noisy and more ‘useful’ difference-Fourier map. (c) Refinement with overestimated weights returns unrealistically ‘nearly clean’ Fourier map and, accordingly, a low GoF. The selected weights for the final refinement were those used in (b).

Figure 6. Difference-Fourier map from the final refinement of theuerdankite structure using an anharmonic approach to the ADP of silver. The colour scheme is the same as in the previous figure; the highest electron density is given in e –/Å3. (a) The Difference-Fourier map from the final refinement and (b) its 3D representation was done in the Vesta program (Momma and Izumi, Reference Momma and Izumi2011). Thermal ellipsoids given at the 75% probability level. Residual positive electron density is displayed in yellow colour (isosurface).
Silver atoms seem to vibrate somewhat anharmonically (Fig. 7) in the theuerdankite structure at room temperature, based on currently obtained high-resolution X-ray diffraction data. Investigating the silver behaviour as a function of temperature would be thus very interesting. Nevertheless, this is beyond the scope of this paper and shall be subject to further studies.

Figure 7. Representation of the anharmonic behaviour of the ADP of silver at room temperature in the crystal structure of theuerdankite as obtained from the non-harmonic refinement of the displacement parameters using JPDF maps.
The conditions of formation
The assemblage of native silver, chlorargyrite, calcite and theuerdankite provides only limited clues about the conditions of the formation of the new mineral. Assuming that these minerals formed together, the presence of silver and chlorargyrite suggests that the redox conditions were near the Ag0/Ag+ redox boundary. The presence of calcite suggests that the solutions were near-neutral.
As chlorargyrite is a fairly common secondary silver mineral, it can be asked if theuerdankite is indeed rare or if it is simply overlooked. In the absence of arsenates other than theuerdankite, no information about the activity of As(V) species in the aqueous solution can be extracted. The solubility of Ca arsenates (e.g. haidingerite) is too high and they are not a part of the observed mineral assemblage.
Thermodynamic properties of the synthetic Ag3AsO4 are known. Wagman et al. (Reference Wagman, Evans, Parker, Schumm, Halow, Bailey, Churney and Nuttall1982) list ΔfGo = –542.6 kJ/mol without references to the original source. Using the appropriate auxiliary data, the solubility constant log K sp for Ag3AsO4 is
Wagman et al. (Reference Wagman, Evans, Parker, Schumm, Halow, Bailey, Churney and Nuttall1982) also provided ΔfGo values for Ag3PO4, Ag2SO4, and AgCl. Inserting all these data into the thermodynamic database of the PHREEQC code (Parkhurst and Appelo, Reference Parkhurst and Appelo1999), some information can be extracted from available data on mine-drainage (MD) waters. Because Ag is rarely analysed, only 20 analyses from almost 1200 analyses in our collection of MD waters yielded saturation indices for the Ag phases. Figure 8a shows that the saturation indices (SI) for theuerdankite are consistently much lower than those of chlorargyrite. The difference is caused by the abundance of Cl– as an anion in most waters. In fact, it is interesting that the SI values for chlorargyrite scatter around 0, meaning that this mineral controls Ag concentrations in the oxidised portions of ore bodies. From these limited data, it seems that theuerdankite can only form if the solutions initially contain Ag in excess of Cl (in molar proportions), such that the Cl concentrations are significantly depressed by the precipitation of AgCl. Hence, theuerdankite can be expected in secondary ores with abundant chlorargyrite and with some source of arsenate. Reduction of Ag+ from the solution and precipitation of secondary native silver will not favour the formation of theuerdankite because it removes Ag, not Cl, from the solution.

Figure 8. (a) Saturation indices for chlorargyrite (diamonds) and theuerdankite (circles) in a range of pH values in mine-drainage waters. (b) Box-and-whiskers diagrams that compare saturation indices of four Ag phases in mine-drainage waters. Boxes show the first and third quartile, the horizontal line the median, and the whiskers the total data range. Data in both (a) and (b) calculated with PHREEQC (Parkhurst and Appelo, Reference Parkhurst and Appelo1999), for details see text.
Calculation of the saturation indices of the other phases (Fig. 8b) shows that the occurrence of Ag3PO4 is even less probable than that of Ag3AsO4. The saturation indices are even lower, and such a potentially new mineral could only form in environments rich in chlorargyrite but unusually poor in arsenate. On the other hand, the saturation indices of Ag2SO4 are quite high but the availability of sulfate can be easily limited by precipitation of common secondary sulfates such as gypsum.
Acknowledgements
The helpful comments of Ian Graham, an Associate Editor, Peter Leverett, Structures Editor and an anonymous reviewer are greatly appreciated. This study was supported by project TERAFIT - CZ.02.01.01/00/22_008/0004594 (JP and VP). Additionally, we acknowledge the support by the Ministry of Culture of the Czech Republic (long-term project DKRVO 2024-2028/1.II.a; National Museum, 00023272) for JS and ZD.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1180/mgm.2024.44.
Competing interests
The authors declare none.