Article contents
K-Na exchange equilibria between muscovite-paragonite solid solution and hydrothermal chloride solutions
Published online by Cambridge University Press: 05 July 2018
Abstract
Three ion exchange equilibrium isotherms between muscovite-paragonite solid solution and 2-molal KCl-NaCl aqueous solutions have been studied at (1) 420°C 1 kbar, (2) 420°C, 2 kbar, and (3) 550°C, 2 kbar. The ΔG°(Joules) ± 2σ of the ion exchange reaction are: ΔG° (1) = −17 259±686, ΔG° (2) = −18 268 ± 560, ΔG° (3) = −16018 ± 336. The excess mixing parameters (‘subregular solution’) of the solid solution (at 1 bar) have been calculated:

The corresponding binodal compositions are (muscovite mol fraction): 12–56% at 420 °C, 1 bar and 15–51% at 550 °C 1 bar. The compositions of micas in equilibrium with perthites (high structural state) at 400, 500, 600 °C and 2 kbar are respectively: Xmus = 91, 86, and 82%.
The mixing properties of the solution were estimated using the speciation of two molal chloride solutions calculated from the dissociation constants of NaCl and KCl in aqueous solution. Although NaCl appears to be substantially more dissociated than KCl, the resulting excess free energy of mixing of the hydrothermal (Na,K)Cl solution was found less than 500 J at temperatures above 400 °C and pressures up to 2 kbar.
The difference in Gibbs free energy of formation (from the elements at 25 °C, 1 bar) between NaCl and KCl in two molal aqueous solutions is proposed:
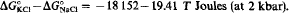
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mineralogical Society of Great Britain and Ireland 1985
References
- 7
- Cited by


