Introduction
Boron is a strategic element used in a variety of products, including ant poisons, detergents (for bleaching), borosilicate glasses (such as Pyrex®), and ceramics (Abe, Reference Abe1952; Woods, Reference Woods1994; Klotz and Moss, Reference Klotz and Moss1996; Yu et al., Reference Yu, Wang, Pang, Zhang, Song, Fu, Hayat and Wang2018; Chen et al., Reference Chen, Ai, Zhang, Liu, Liu, Pan and Liu2020; U.S.G.S, 2022). The strategic importance of boron, and the moderate supply risk due to its uneven distribution, has been recognised by the European Union, which has classified borates as critical raw material since 2014 (European Commission, 2014). Economically viable boron mineral deposits are distributed irregularly worldwide and are mostly represented by five main hydrated borate minerals: ulexite, colemanite, borax, tincalconite and kernite (Kistler and Helvacı, Reference Kistler, Helvacı and Carr1994; Helvaci and Alonso, Reference Helvaci and Alonso2000; Zheng et al., Reference Zheng, Qi and Yuan2005; García-Veigas and Helvacı, Reference García-Veigas and Helvacı2013). Other borate minerals, such as inderborite, meyerhofferite, inyoite and tertschite, are often found in smaller weight fractions alongside these main minerals. Due to their low production cost, hydrated borates are believed to be good candidates as aggregates in neutron shielding concretes (Okuno, Reference Okuno2005; Okuno et al., Reference Okuno, Kawai and Yamada2009; Glinicki et al., Reference Glinicki, Antolik and Gawlicki2018), because of the 10B isotope (which accounts for ~20% of natural boron) high cross-section for thermal neutrons (~3840 barns) (Carter et al., Reference Carter, Palevsky, Myers and Hughes1953; Palmer and Swihart, Reference Palmer, Swihart, Anovitz and Grew1996), leading to the reaction:
Inderborite, ideally CaMg[B3O3(OH)5]2(H2O)4⋅2H2O, space group C2/c with a ≈ 12.14, b ≈ 7.43, c ≈ 19.23 Å and β ≈ 90.3°, was originally discovered at the Inder Lake borate deposit, western Kazakhstan, and later also at the Eskişehir district, Turkey (Kurkutova et al., Reference Kurkutova, Rumanova and Belov1965; Palmer and Helvaci, Reference Palmer and Helvaci1997). The lower occurrence of inderborite, with respect to other most common borates, is attributed to its extremely narrow stability field in the CaO–MgO–B2O3–H2O system, as demonstrated by Birsoy and Özbaş (Reference Birsoy and Özbaş2012). However, minor fractions of inderborite are commonly found associated with colemanite and ulexite in valuable ore deposits of hydrate borates (e.g. Kirka and Sarikaya deposits) (Palmer and Helvaci, Reference Palmer and Helvaci1997; Helvacı and Palmer, Reference Helvacı and Palmer2017). For example, inderborite has been found in the ore debris near the Kuşkaya gallery of the Turkish Borax Mining Company, in the Sarikaya borate deposits, alongside other borate minerals such as colemanite, borax, ulexite, kurnakovite and inderite (Baysal, Reference Baysal1973).
Kurkutova et al. (Reference Kurkutova, Rumanova and Belov1965) were the first to determine the crystal structure of inderborite (Fig. 1), although the complex hydrogen bond network was only described later by Burns and Hawthorne (Reference Burns and Hawthorne1994). In a recent paper, based on a multi-methodological approach, the crystal chemistry (with a focus on the B isotopic composition) and structure of inderborite (based on a single-crystal neutron diffraction experiment) were re-investigated by Gatta et al. (Reference Gatta, Cannaò, Comboni, Battiston and Fabelo2023). They confirmed that the chemical composition of the inderborite from Inder, Kazakhstan is virtually identical to the ideal one. The fundamental building block (FBB) of inderborite is a [B3O3(OH)5]2– ring, consisting of 2 Bφ4 tetrahedrons and one planar trigonal Bφ3 unit (φ represents an O2– anion, an OH– hydroxyl group or a H2O molecule). The same <Δ2□> unit (Δ stands for a Bφ3 unit, and □ for a Bφ4 tetrahedron), in which all oxygen atoms that are not shared between two boron atoms are protonated (Burns and Hawthorne, Reference Burns and Hawthorne1994), occurs also in kurnakovite, meyerhofferite, inyoite, inderite and solongoite, whereas in hydroboracite and colemanite it is polymerised into chains (Hawthorne, Reference Hawthorne2012). In the crystal structure of inderborite, the [B3O3(OH)5]2– rings are interconnected with the Ca-polyhedra and Mg-octahedra through the O1, O2, O3, O6 and O8 oxygen hinges. This results in the formation of continuous hetero-polyhedral sheets parallel to (100) (Fig. 1), connected through a complex hydrogen bonding network involving O7 and O4 as acceptors, respectively from the O3 and O6 hydroxyl groups and from the O10 H2O molecule. A crucial role in providing stability to the crystal structure is attributed to the interstitial (‘zeolitic’) H2O molecule O11, which occupies a key position between the sheets (Fig. 1). O11 is connected, via hydrogen bonding, to O8 and O9: the former is an oxygen hinge that connects the Mg-octahedron with the B2-tetrahedron, whereas the latter is a H2O molecule belonging only to the Mg-octahedron. This further connects the crystal structure along the [010] crystallographic direction. O9 is also a donor to O10, the only H2O molecule of the complex Ca polyhedrons, providing the only weak connection between Ca- and Mg-polyhedrons.

Figure 1. Inderborite structure, based on the model proposed by Gatta et al. (Reference Gatta, Cannaò, Comboni, Battiston and Fabelo2023), viewed perpendicular to the (100) plane. Ca-polyhedrons in indigo, Mg-polyhedrons in orange, boron polyhedrons in green, hydrogen in small pale pink spheres. Drawn using VESTA software (Momma and Izumi, Reference Momma and Izumi2008),
At the present time, inderborite remains an extremely poorly studied mineral. The only available Raman spectrum to date can be found on the https://rruff.info/ website, and some important thermodynamic parameters (such as the thermal expansion coefficient and elastic compressibility) are still missing. As pointed out by Gatta et al. (Reference Gatta, Cannaò, Comboni, Battiston and Fabelo2023), given the importance of the hydrogen bonding network in inderborite, a compressional, thermal, or chemical perturbation of the H-bonding scheme could easily lead to a phase transition. On this basis, in this study we aim to: (1) assess the stability range of inderborite with respect to pressure, including for potential industrial utilisation of this borate; and (2) describe the structural evolution of inderborite, at the atomic scale, with increasing pressure. While inderborite is not likely to be used as primary component in radiation shielding concretes, its association with major hydrated borates (e.g. colemanite and borax) makes it imperative to investigate its stability under non-ambient conditions. Furthermore, its stability at high-pressure allows (3) comparisons to be drawn with other hydrated borate structures studied and to strengthen the hypothesis of a correlation between the total H2O content and the stability range of hydrated borates under pressure.
Experimental procedures
The sample of inderborite used in this study comes from the type locality (Inder Deposit, Kazakhstan), and was provided by the late Dr. Renato Pagano. Crystals from the same sample were recently used for the experiments reported by Gatta et al. (Reference Gatta, Cannaò, Comboni, Battiston and Fabelo2023). Inderborite is a light (1.92 g/cm3) and soft (3.5 on the Mohs scale) mineral with a prismatic habit. Two single crystals, each measuring ~20×15×10 μm, were selected for high-pressure experiments at the ID15b beamline, ESRF, Grenoble, France. The diffraction experiment employed a convergent monochromatic beam (E ≈ 30 keV, λ ≈ 0.41 Å and ⁓200 mA). Helium was used as the pressure-transmitting fluid (Klotz et al., Reference Klotz, Chervin, Munsch and Le Marchand2009), and two ruby micro-spheres were added as pressure calibrants (pressure uncertainty ± 0.05 GPa; Mao et al., Reference Mao, Xu and Bell1986). The crystals were loaded in two different membrane-driven DACs (diamond anvil cells), with 600 μm culet Boehler-Almax design anvils. For each DAC, a stainless-steel foil (with thickness of ~250 μm) was pre-indented to ~80 μm and then drilled by spark-erosion, leading to a P-chamber of ~300 μm in diameter. The diffraction patterns were collected by an Eiger2X 9M detector, positioned ~180 mm from the sample. The sample-to-detector distance was calibrated using a Si standard and a vanadinite (Pb5(VO4)3Cl) single crystal. A pure ω-scan (−32°≤ ω ≤ +32°) was used to collect the diffraction patterns, with a 0.5° step width and a 0.5 s exposure time per step. Further details on the beamline setup can be found in Hanfland (Reference Hanfland2016) and Poreba et al. (Reference Poreba, Comboni, Mezouar, Hanfland and Garbarino2022).
Data analysis
The CrysAlisPro package (Rigaku Oxford Diffraction, 2019) was used to index the diffraction peaks and integrate their intensities; corrections for Lorentz-polarisation effects were also applied. The semi-empirical ABSPACK routine, implemented in CrysAlisPro, was used to account for X-ray absorption effects caused by the DAC components. Table 1 lists the unit-cell parameters at high pressure, and their evolution with P is shown in Fig. 2. Selected diffraction patterns are also presented in Fig. 3. The JANA2006 package (Petrícek et al., Reference Petrícek, Dušek and Palatinus2014) was used for all structure refinements, with the initial fractional coordinates taken from Burns and Hawthorne (Reference Burns and Hawthorne1994) and Gatta et al. (Reference Gatta, Cannaò, Comboni, Battiston and Fabelo2023). The CIFs (crystallographic information files) are deposited as supplementary materials (see below).
Table 1. Evolution of the unit-cell parameters of inderborite with pressure obtained from the two independent experiments (*high-pressure polymorph).


Figure 2. Evolution with pressure of the unit-cell parameters of inderborite: first dataset in black squares, second dataset in red diamonds, inderborite-II in green circles. Estimated standard deviations are smaller than symbols.

Figure 3. Reconstruction, based on the experimental data, of the 0kl*, hk0* and h0l* reciprocal lattice planes of inderborite- (left side) and inderborite-II (right side). Above the phase transition, the number of observed reflections dropped dramatically.
High-pressure data were collected up to 9.84(5) GPa, as the number and intensity of the observed reflections [i.e. with F o2 > 3σ(F o2)] decreased significantly after the phase transition at 8.80(5) GPa (as Fig. 3 shows), effectively ending the experiment. In both the experiments, crystals did not recover after the phase transition. This was the most destructive phase transition observed in hydrated borates to date (compare Comboni et al., Reference Comboni, Pagliaro, Gatta, Lotti, Milani, Merlini, Battiston, Glazyrin and Liermann2020b, Reference Comboni, Battiston, Pagliaro, Lotti, Gatta and Hanfland2022a), as the number of observed reflections was barely enough to properly index the diffraction pattern of the high-pressure polymorph, inderborite-II, which was found to be metrically monoclinic. The space group has not been unambiguously determined.
Relevant interatomic distances, average bond lengths, angles, polyhedral volumes, distortion index [defined as D = ${1 \over n}\mathop \sum \limits_{i = 1}^n {{\vert {l_i-l_{av}} \vert } \over {l_{av}}}$![]() , where l i is the distance from the central atom to the i th coordinating atom, and l avis the average bond length; Baur, Reference Baur1974], quadratic elongation [defined as <λ>= ${1 \over n}\mathop \sum \limits_{i = 1}^n \left({{{l_i} \over {l_0}}} \right)^2$
, where l i is the distance from the central atom to the i th coordinating atom, and l avis the average bond length; Baur, Reference Baur1974], quadratic elongation [defined as <λ>= ${1 \over n}\mathop \sum \limits_{i = 1}^n \left({{{l_i} \over {l_0}}} \right)^2$![]() , where l 0 is the center-to-vertex distance of a regular polyhedron of the same volume and l i is the actual centre-to-vertex length; Robinson et al., Reference Robinson, Gibbs and Ribbe1971] and bond angle variance [defined as σ2= ${1 \over {m-1}}\mathop \sum \limits_{i = 1}^m ( {\rm\phi_i-\rm\phi_0} ) ^2$
, where l 0 is the center-to-vertex distance of a regular polyhedron of the same volume and l i is the actual centre-to-vertex length; Robinson et al., Reference Robinson, Gibbs and Ribbe1971] and bond angle variance [defined as σ2= ${1 \over {m-1}}\mathop \sum \limits_{i = 1}^m ( {\rm\phi_i-\rm\phi_0} ) ^2$![]() where m is the number of faces in the polyhedron×3/2, i.e. number of bond angles, ϕi is the i th bond angle, and ϕ0 is the ideal bond angle for a regular polyhedron e.g. 90° for an octahedron; Robinson et al., Reference Robinson, Gibbs and Ribbe1971] have been calculated using the tools implemented in the VESTA software (Momma and Izumi, Reference Momma and Izumi2008), and are listed in Supplementary Table S1. Relevant interatomic angles and distances are reported in Table 2.
where m is the number of faces in the polyhedron×3/2, i.e. number of bond angles, ϕi is the i th bond angle, and ϕ0 is the ideal bond angle for a regular polyhedron e.g. 90° for an octahedron; Robinson et al., Reference Robinson, Gibbs and Ribbe1971] have been calculated using the tools implemented in the VESTA software (Momma and Izumi, Reference Momma and Izumi2008), and are listed in Supplementary Table S1. Relevant interatomic angles and distances are reported in Table 2.
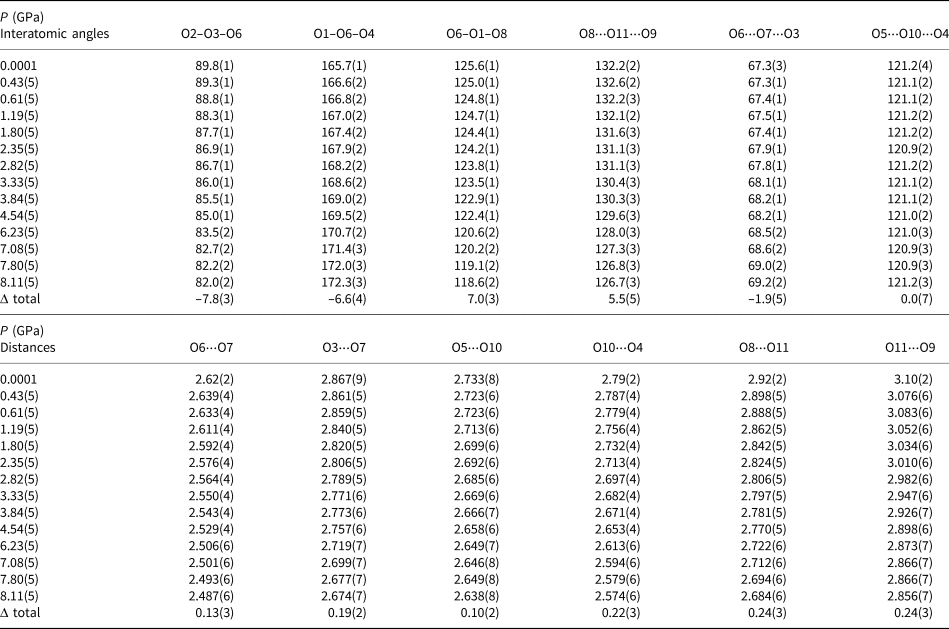
Table 2. Evolution, with pressure, of some relevant interatomic angles (in °) and distances (d in Å) in inderborite structure [Δ defined as the difference between the value at 0.0001 GPa and that at 8.11 GPa].
To describe the isothermal behaviour of inderborite, a second-order Birch–Murnaghan Equation of State (BM–EoS) was fitted to the P–V data (Birch, Reference Birch1947). This EoS allows refinement of the bulk modulus [KV0 or KP0,T0, defined as –V0(∂P/∂V)T0 = β–1P0,T0, where βP0,T0 is the volume compressibility coefficient at room conditions] and its P-derivatives [K’=∂KP0,T0/∂P and K’’=∂2KP0,T0/∂P 2]. When truncated to the second order in energy, i.e. with K’= ∂KP0,T0/∂P = 4, the EoS transforms to:
where fe [defined as $fe = \left[{{\left({{{V_0} \over V}} \right)}^{{2 \over 3}}-1} \right]/2$![]() ] is the Eulerian finite strain. The truncation to the second order in energy is reasonable when the experimental data plot following a horizontal trend in the diagram with Eulerian strain vs. ‘normalised pressure’ [F, defined as F = P/[3fe(1 + 2fe)5/2]]. The BM–EoS parameters (listed in Table 3) were refined by minimising the differences between the EoS curves and the experimental data, which were weighted by their uncertainties in P and V. The fitting was carried out using the EOS-FIT7-GUI software (Angel et al., Reference Angel, Gonzalez-Platas and Alvaro2014; Gonzalez-Platas et al., Reference Gonzalez-Platas, Alvaro, Nestola and Angel2016). An estimated uncertainty of ± 0.05 GPa was considered for pressure (Mao et al., Reference Mao, Xu and Bell1986) during the data fitting. The fe vs F plot is shown in Supplementary Fig. S1.
] is the Eulerian finite strain. The truncation to the second order in energy is reasonable when the experimental data plot following a horizontal trend in the diagram with Eulerian strain vs. ‘normalised pressure’ [F, defined as F = P/[3fe(1 + 2fe)5/2]]. The BM–EoS parameters (listed in Table 3) were refined by minimising the differences between the EoS curves and the experimental data, which were weighted by their uncertainties in P and V. The fitting was carried out using the EOS-FIT7-GUI software (Angel et al., Reference Angel, Gonzalez-Platas and Alvaro2014; Gonzalez-Platas et al., Reference Gonzalez-Platas, Alvaro, Nestola and Angel2016). An estimated uncertainty of ± 0.05 GPa was considered for pressure (Mao et al., Reference Mao, Xu and Bell1986) during the data fitting. The fe vs F plot is shown in Supplementary Fig. S1.
Table 3. Refined elastic parameters of the inderborite unit-cell and of the coordination polyhedrons, based on the isothermal II-BM Equation of State fit (*fixed parameter).

Results
Elastic behaviour
The linear elastic parameters, listed in Table 3, suggest that inderborite is a rather isotropic mineral, which deforms almost equally along the principal crystallographic directions. However, as expected in monoclinic crystals, the unit-cell angle β is free to vary with pressure, meaning that the linear bulk moduli along the principal crystallographic directions (listed in Table 3) do not actually describe the compressional anisotropy. To overcome this problem, the Eulerian finite strain analysis was performed with the Win_Strain software (Angel, Reference Angel2011). The geometrical relationships between the unit-strain ellipsoid and the crystallographic axes of inderborite can be described by the following matrix (with ɛ1>ɛ2>ɛ3):

for inderborite, between 0.0001 and 8.11(5) GPa, ɛ1:ɛ2:ɛ3 = 1.4:1.05:1 [ɛ1 = 0.00723(5) GPa–1; ɛ2 = 0.00546(3) GPa–1; and ɛ3 = 0.00524(4) GPa–1]. The inderborite response to compression is only moderately anisotropic, with the major direction (ɛ1) of compression describing an angle of only 10° with the c axis. This finding is surprising if compared to other hydrous borates, such as meyerhofferite (ɛ1:ɛ2:ɛ3 = 5.8:4.7:1) or inyoite (ɛ1:ɛ2:ɛ3= 3.5:2.1:1) (Comboni et al., Reference Comboni, Pagliaro, Gatta, Lotti, Battiston, Garbarino and Hanfland2020a, Reference Comboni, Battiston, Pagliaro, Lotti, Gatta and Hanfland2022a). Regarding the high-pressure polymorph, the poor quality of the diffraction data did not allow any robust calculation, as discussed above. However, the previous matrix, showing the unit-strain ellipsoid calculated between 0.0001 and 8.11(5) GPa, does not describe the P-induced evolution of the strain ellipsoid itself, which undergoes a significant change as pressure increases. Initially, between 0.0001 and 2.35(5) GPa, the unit-strain ellipsoid is described by the following matrix:

with ɛ1:ɛ2:ɛ3 = 1.3:1.1:1 [ɛ1 = 0.0079(2) GPa–1; ɛ2 = 0.0070(2) GPa–1; and ɛ3 = 0.0062(1) GPa–1]. Therefore, in the initial stage of compression, ɛ1 and ɛ2 lie on the ac plane, whereas ɛ3 is parallel to b. However, as pressure increases, ɛ1, ɛ2 and ɛ3 deviate from the original orientation and, between 6.23(5) and 8.11(5) GPa, the unit-strain ellipsoid matrix changes to:

with ɛ1:ɛ2:ɛ3 = 1.7:1:1 [ɛ1 = 0.0063(2) GPa–1; ɛ2 = 0.0037(6) GPa–1; ɛ3 = 0.0036(5) GPa–1]. Close to the phase transition, magnitude and orientation of the unit-strain ellipsoid differ from the earlier stages of compression, with ɛ1 being almost parallel to c, ɛ3 almost parallel to a, and ɛ2 parallel to b.
Structure evolution
Referring to the first dataset (Table 1), between ambient pressure and 8.11(5) GPa, the length of the unit-cell edges of inderborite decreases steadily by ~4.3% for the a and b unit-cell edges and by ~3.3% along the c edge. The unit-cell volume decreases monotonically by ~13.5% and the β angle steadily increases by ~3.3% (see Table 1). Similar values (i.e. within 3σ) were observed for the second dataset. Up to 8.11(5) GPa, the crystal structure of inderborite deforms steadily with no significant changes. Between 8.11(5) and 8.80(5) GPa, inderborite undergoes a phase transition to its high-pressure polymorph, inderborite-II. This phase transition is rather disruptive, and data were collected only up to 10.10(5) GPa, as the number and intensity of the observed reflections [i.e. with F o2 > 3σ(F o2)] decreased significantly after the phase transition (down to ~60). The phase transition is marked by a sharp volume decrease, typical of first-order phase transformations. Upon decompression, the crystal structure of inderborite does not revert to its ambient pressure polymorph, indicating that the transition is irreversible (at least for the time scale of our experiment).
Discussion
The high-quality structural refinements of inderborite with pressure allowed a full description of the main deformation mechanisms able to accommodate the effect of compression. The bulk modulus (KV0) of the Bφ4 tetrahedra, based on the isothermal Birch–Murnaghan Equation of State fit (Table 3), is more than five times higher than that of the inderborite unit cell. This suggests that the boron tetrahedrons act as uncompressible units, as expected at low–mid pressures (Table 3 and Supplementary Table S1). The same behaviour has been observed in all the hydrated borates studied so far at high pressure (e.g. ulexite, jadarite and kernite; Comboni et al., Reference Comboni, Pagliaro, Gatta, Lotti, Milani, Merlini, Battiston, Glazyrin and Liermann2020b, Reference Comboni, Pagliaro, Gatta, Lotti, Battiston, Merlini and Hanfland2021a, Reference Comboni, Battiston, Rumsey, Pagliaro, Lotti, Hanfland and Gatta2022b) and in other minerals as well (e.g. reedmergnerite, londonite and barium metaborates, Gatta et al., Reference Gatta, Vignola and Lee2011; Bekker et al., Reference Bekker, Podborodnikov, Sagatov, Shatskiy, Rashchenko, Sagatova, Davydov and Litasov2022; Gorelova et al., Reference Gorelova, Pakhomova, Aprilis, Yin, Laniel, Winkler, Krivovichev, Pekov, Dubrovinskaia and Dubrovinsky2022). On the other hand, the Mgφ6 octahedra and Caφ8 polyhedrons are significantly softer but with an important difference. The Ca-polyhedron compresses as expected, similar to observations in other hydrous borate crystal structures, such as meyerhofferite and inyoite, as evidenced by its bulk modulus (53(4) GPa) that is within 1σ of the values observed in meyerhofferite and inyoite (Comboni et al., Reference Comboni, Pagliaro, Gatta, Lotti, Battiston, Garbarino and Hanfland2020a, Reference Comboni, Battiston, Pagliaro, Lotti, Gatta and Hanfland2022a). In contrast, the Mg-polyhedron is significantly stiffer with respect to Mg-polyhedra in other structures: the calculated bulk modulus in this study (81(8) GPa) is 11% higher than that of the same polyhedron in kurnakovite and ~20% higher than that in inderite (67(4) GPa) (Pagliaro et al., Reference Pagliaro, Lotti, Battiston, Comboni, Gatta, Cámara, Milani, Merlini, Glazyrin and Liermann2021; Comboni et al., Reference Comboni, Poreba, Battiston, Hanfland and Gatta2023). Although considerably stiff, the Mg–φ6 polyhedron compression is highly anisotropic. In the experimental pressure range of this study, while the Mg–O9 and the Mg–O2 distances decrease by ~1.8 and 1.5%, Mg–O8 decreases by ~4%. This anisotropic compression, mainly affecting the Mg–O8 bond, leads to a progressive distortion of the Mg–φ6 octahedron, as indicated by the progressive increase of the distortion index (σ2) values (Supplementary Table S1). Overall, when compared to the bulk modulus of inderborite, all the polyhedrons are stiffer than the overall structure (see Table 3), meaning that the structural deformation in response to the applied pressure must be accommodated by other mechanisms. Indeed, tilting around the oxygen hinges between the B-, Ca- and Mg- polyhedrons can be deduced from the data in Table 2, which reports O–O–O angles that change significantly with pressure. In detail, the O2–$\rm \widehat{{O3}}$![]() –O6, O1–$\rm\widehat{{O6}}$
–O6, O1–$\rm\widehat{{O6}}$![]() –O4 and O6–$\rm\widehat{{O1}}$
–O4 and O6–$\rm\widehat{{O1}}$![]() –O8 angles, which describe the degree of tilting between the [B3O3(OH)5]2– polyion and the Ca–φ8 octahedron, show a steady and progressive deformation as pressure increases [O2–$\rm\widehat{{O3}}$
–O8 angles, which describe the degree of tilting between the [B3O3(OH)5]2– polyion and the Ca–φ8 octahedron, show a steady and progressive deformation as pressure increases [O2–$\rm\widehat{{O3}}$![]() –O6, O1–$\rm\widehat{{O6}}$
–O6, O1–$\rm\widehat{{O6}}$![]() –O4 decrease by ~7.8(2)° and 6.6(2)°, whereas O6–$\rm\widehat{{O1}}$
–O4 decrease by ~7.8(2)° and 6.6(2)°, whereas O6–$\rm\widehat{{O1}}$![]() –O8 increases by ~7.0(2)°]. The compression of the hydrogen-bonding network also accommodates part of the pressure-induced deformation and the interstitial (‘zeolitic’) H2O molecule O11 might play a role in the destabilisation of the crystal structure. This molecule is connected, via hydrogen bonding, with the O8 hydroxyl group and the O9 H2O molecules (Fig. 1, Supplementary Fig. S2). At ambient pressure, the interatomic angle O8⋅⋅⋅$\rm\widehat{{O11}}$
–O8 increases by ~7.0(2)°]. The compression of the hydrogen-bonding network also accommodates part of the pressure-induced deformation and the interstitial (‘zeolitic’) H2O molecule O11 might play a role in the destabilisation of the crystal structure. This molecule is connected, via hydrogen bonding, with the O8 hydroxyl group and the O9 H2O molecules (Fig. 1, Supplementary Fig. S2). At ambient pressure, the interatomic angle O8⋅⋅⋅$\rm\widehat{{O11}}$![]() ⋅⋅⋅O9 is 132.2(2)°, and it only remains roughly constant in the very first GPa of compression, decreasing progressively with increasing pressure (Table 2). This is paired with a steady decreasing of the O11⋅⋅⋅O9 and O11⋅⋅⋅O8 distances (Table 2), which decrease by ~8.4 and 7.9%. These are not the only atoms of oxygen connected via hydrogen bonding affected by the structure deformation. Indeed, the interatomic O6⋅⋅⋅$\rm\widehat{{O3}}$
⋅⋅⋅O9 is 132.2(2)°, and it only remains roughly constant in the very first GPa of compression, decreasing progressively with increasing pressure (Table 2). This is paired with a steady decreasing of the O11⋅⋅⋅O9 and O11⋅⋅⋅O8 distances (Table 2), which decrease by ~8.4 and 7.9%. These are not the only atoms of oxygen connected via hydrogen bonding affected by the structure deformation. Indeed, the interatomic O6⋅⋅⋅$\rm\widehat{{O3}}$![]() ⋅⋅⋅O7 angle, which is formed by the oxygen atom O7 (being part of the B2-tetrahedron), acceptor of two hydrogen bonds from the hydroxyl groups O3 and O6 (which belong to the Ca-polyhedron), deforms steadily as pressure increases (Table 2). In addition O11⋅⋅⋅O9 and O11⋅⋅⋅O8, together with the interatomic distances O6⋅⋅⋅O7 and O7⋅⋅⋅O3, decrease drastically with pressure (of ~5 and 6.7%, Table 2). The H2O molecule O10 is the donor of two hydrogen bonds, with O4 and O5 as acceptors (Supplementary Fig. S2), two atoms of oxygen that act as hinges in the [B3O3(OH)5]2– polyion. The interatomic angle O5⋅⋅⋅$\rm\widehat{{O10}}$
⋅⋅⋅O7 angle, which is formed by the oxygen atom O7 (being part of the B2-tetrahedron), acceptor of two hydrogen bonds from the hydroxyl groups O3 and O6 (which belong to the Ca-polyhedron), deforms steadily as pressure increases (Table 2). In addition O11⋅⋅⋅O9 and O11⋅⋅⋅O8, together with the interatomic distances O6⋅⋅⋅O7 and O7⋅⋅⋅O3, decrease drastically with pressure (of ~5 and 6.7%, Table 2). The H2O molecule O10 is the donor of two hydrogen bonds, with O4 and O5 as acceptors (Supplementary Fig. S2), two atoms of oxygen that act as hinges in the [B3O3(OH)5]2– polyion. The interatomic angle O5⋅⋅⋅$\rm\widehat{{O10}}$![]() ⋅⋅⋅O4 remains unchanged (within 1σ) up to 8.11(5), GPa, however the distances between the acceptors (O4 and O5) and the donor (O10) progressively decrease of ~7.9 and 3.7%, respectively. Therefore, the interaction between the oxygen pairs O10⋅⋅⋅O4 and O10⋅⋅⋅O5 increases steadily with pressure. The compression of the hydrogen bond network is significantly larger with respect to the average decrease of the Ca–O, Mg–O and B–O distances (⁓4%, ⁓2% and ⁓1.6%, respectively), further highlighting that the main mechanisms with which the structure deforms are (1) the tilting around inter-polyhedral oxygen hinges and (2) compression of the hydrogen bonding network. This phenomenon is analogous to what was observed in several other hydrated borate structures characterised by a pervasive hydrogen bonding network, which plays a paramount role in the stability of the crystalline edifice (e.g. meyerhofferite and inyoite; Comboni et al., Reference Comboni, Poreba, Pagliaro, Battiston, Lotti, Gatta and Garbarino2021b, Reference Comboni, Battiston, Pagliaro, Lotti, Gatta and Hanfland2022a). It is likely that the combination of these two deformation mechanisms induces the changes of the orientation of the unit strain ellipsoid, ultimately affecting the elasticity and the (very moderate) anisotropy of inderborite. Supplementary Fig. S4 shows the evolution of the O⋅⋅⋅O distance (reported in Table 2) with pressure. Note that the slopes of such trends change manifestly with pressure, so this can be correlated potentially to the changes in the unit-strain ellipsoid configuration, highlighting, once again, the role of the hydrogen-bonding network on the stability of the crystal structure.
⋅⋅⋅O4 remains unchanged (within 1σ) up to 8.11(5), GPa, however the distances between the acceptors (O4 and O5) and the donor (O10) progressively decrease of ~7.9 and 3.7%, respectively. Therefore, the interaction between the oxygen pairs O10⋅⋅⋅O4 and O10⋅⋅⋅O5 increases steadily with pressure. The compression of the hydrogen bond network is significantly larger with respect to the average decrease of the Ca–O, Mg–O and B–O distances (⁓4%, ⁓2% and ⁓1.6%, respectively), further highlighting that the main mechanisms with which the structure deforms are (1) the tilting around inter-polyhedral oxygen hinges and (2) compression of the hydrogen bonding network. This phenomenon is analogous to what was observed in several other hydrated borate structures characterised by a pervasive hydrogen bonding network, which plays a paramount role in the stability of the crystalline edifice (e.g. meyerhofferite and inyoite; Comboni et al., Reference Comboni, Poreba, Pagliaro, Battiston, Lotti, Gatta and Garbarino2021b, Reference Comboni, Battiston, Pagliaro, Lotti, Gatta and Hanfland2022a). It is likely that the combination of these two deformation mechanisms induces the changes of the orientation of the unit strain ellipsoid, ultimately affecting the elasticity and the (very moderate) anisotropy of inderborite. Supplementary Fig. S4 shows the evolution of the O⋅⋅⋅O distance (reported in Table 2) with pressure. Note that the slopes of such trends change manifestly with pressure, so this can be correlated potentially to the changes in the unit-strain ellipsoid configuration, highlighting, once again, the role of the hydrogen-bonding network on the stability of the crystal structure.
Concluding remarks
In this study, we have investigated the high-pressure behaviour of inderborite through in situ single crystal X-ray diffraction, up to ~10 GPa. Data collected at high-pressure revealed that:
(1) The ambient-condition polymorph of inderborite remains stable up to ~8 GPa. Between 8.11(5) and 8.80(5) GPa, inderborite undergoes a first-order phase transition. The space group of inderborite-II, which is metrically monoclinic, remains unclear. The phase transition (which is not reversible) is marked by a volume decrease of ~7.0%.
(2) The elastic parameters of inderborite have been determined, and the elastic behaviour has been described in detail. These data will contribute to improving the thermodynamic database of hydrous borates.
(3) With increasing pressure, the volume compression is accommodated primarily by the deformation (and compression) of the hydrogen bonding network, as well as by the tilting of the Ca-, Mg- and B- polyhedrons around the bridging oxygen sites.
(4) The pressure at which the inderborite-to-inderborite-II phase transition occurs (8.5 ± 0.40 GPa) follows the trend observed in most hydrated borates studied so far (Comboni et al., Reference Comboni, Pagliaro, Gatta, Lotti, Battiston, Garbarino and Hanfland2020a, Reference Comboni, Pagliaro, Gatta, Lotti, Battiston, Merlini and Hanfland2021a, Reference Comboni, Battiston, Pagliaro, Lotti, Gatta and Hanfland2022a; Pagliaro et al., Reference Pagliaro, Lotti, Battiston, Comboni, Gatta, Cámara, Milani, Merlini, Glazyrin and Liermann2021), excluding inderite (Comboni et al., Reference Comboni, Poreba, Battiston, Hanfland and Gatta2023). This finding strengthens the presumed correlation between the pressure at which the phase transition occurs and the total H2O content (in wt.%, Supplementary Fig. S3).
(5) The bulk modulus of inderborite (KV 0 = 41(1) GPa) is similar to the bulk modulus of quartz (~37 GPa) and lower than those of other aggregates used in radiation shielding concretes (e.g. colemanite KV0 = 67(4); Okuno, 2005; Lotti et al., Reference Lotti, Gatta, Comboni, Guastella, Merlini, Guastoni and Liermann2017). Similarly to colemanite and inderite, inderborite is a Na-free borate, meaning that it cannot promote ASR reactions (i.e. ‘alkali-silica reactions’; Thomas, Reference Thomas2011; Figueira et al., Reference Figueira, Sousa, Coelho, Azenha, de Almeida, Jorge and Silva2019; Mohammadi et al., Reference Mohammadi, Ghiasvand and Nili2020), which are known to undermine the durability of Portland cements. Considering the stability field of inderborite at high pressure and its elastic parameters, this borate can potentially be used as a B-rich aggregate in radiation-shielding materials.
Acknowledgements
ESRF is thanked for the allocation of the beamtime (proposal MA-5273, doi: 10.15151/ESRF-ES 656089266). GDG, DC, PL and TB acknowledge the support of the Italian Ministry of Education (MIUR) through the project “PRIN2017 - Mineral reactivity, a key to understand large-scale processes” (2017L83S77) and of the University of Milan through the project Piano di Sostegno alla Ricerca 2022. The work was partly supported by the Italian Ministry for Universities and Research (MUR) through the project “Dipartimenti di Eccellenza 2023–2027”.
Supplementary material
The supplementary material for this article (Figs S1–4 and Table S1) can be found at https://doi.org/10.1180/mgm.2024.29.
Competing interests
The authors declare none.








