Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T08:32:24.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Time-dependent Landau theory for order/disorder processes in minerals

Published online by Cambridge University Press:  05 July 2018

M. A. Carpenter  and
E. Salje
M. A. Carpenter
Affiliation:
Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge CB2 3EQ
E. Salje
Affiliation:
Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge CB2 3EQ
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent advances in the use of time-dependent order parameter theory to describe the kinetics of order/disorder transitions are reviewed. The time dependence of a macroscopic order parameter, Q, follows, to a good approximation:

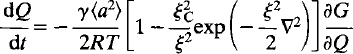
For systems in which the order parameter has a long correlation length (large ξ) and is not conserved (small ξC), the Ginzburg-Landau equation provides a general kinetic solution:

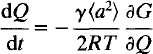
Specific rate laws can be derived from this general solution depending on whether the crystals remain homogeneous with respect to the order parameter, Q. The advantages of the overall approach are, firstly, that it does not depend on the detailed structure of the material being examined; secondly, that the order parameter can be followed experimentally through its relationship with other properties, such as spontaneous strain, excess entropy, intensities of superlattice reflections, etc.; and, finally, that conventional Landau expansions in Q may be used to describe the thermodynamic driving forces.

For a simple second-order transition in crystals which remain homogeneous in Q the rate law is:

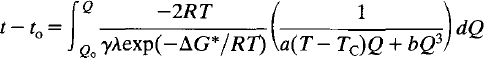
If the free energy of activation varies with the state of order of the crystal, this becomes:

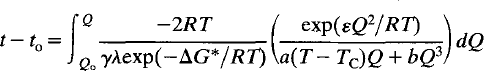
Simplifying assumptions can be introduced into the mathematics, or the integrals can be solved numerically. For crystals which remain homogeneous, the simplest solution valid only over small deviations from equilibrium is:

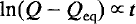
For crystals which develop heterogeneities in Q, the rate laws change significantly and we find as an extreme case:

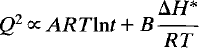
where the A coefficient may be temperature dependent.

Experimental data available for a limited number of minerals (omphacite, anorthite, albite, cordierite and nepheline) are used to demonstrate the practical implications of the overall approach. As anticipated from the theory, modulated structures commonly develop during kinetic experiments, the observed rate laws depend on whether the critical point of the ordering is located at the centre or boundary of the Brillouin zone, and the rate laws for ordering and disordering can be quite different. The importance of different length scales, not only in the different techniques for characterizing states of order (IR, NMR, calorimetry, X-ray diffraction, etc.) but also for interpreting observed mechanisms and rate laws, is also outlined.

Use of the order parameter in Landau expansions and in Ginzburg-Landau rate laws provides, in principle, a means of predicting the equilibrium and non-equilibrium evolution of minerals in nature.

Keywords

time-dependent Landau theoryorder/disorder processes
Type
Mineralogy
Information
Mineralogical Magazine , Volume 53 , Issue 372 , September 1989 , pp. 483 - 504
Copyright
Copyright © The Mineralogical Society of Great Britain and Ireland 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Als-Nielsen, J. and Birgeneau, R. J. (1977) Mean field theory, the Ginzbug criterion, and marginal dimensionality of phase transitions. Am. J. Phys. 45, 554-60.CrossRefGoogle Scholar
Becker, R. (1978) Theorie der Wiirme. Springer-Verlag. 336pp.CrossRefGoogle Scholar
Binder, K. (1987) Theory of first order transitions. Rep. Progr. Phys. 50, 783-859.CrossRefGoogle Scholar
Buseck, P. R., Nord, G. L. Jr. and Veblen, D. R. (1980) Subsolidus phenomena in pyroxenes. In Pyroxenes (Prewitt, C. T., ed.) Min. Soc. Am. Reviews in Mineralogy 7, 117-211.CrossRefGoogle Scholar
Cahn, J. W. (1961) On spinodal decomposition. Acta Met. 9, 795-801.CrossRefGoogle Scholar
Cahn, J. W. (1962) On spinodal decomposition in cubic crystals. Ibid. 10, 179-83.CrossRefGoogle Scholar
Cahn, J. W. (1968) Spinodal decomposition. Trans. AIME 242, 166-80.Google Scholar
Cameron, M. and Papike, J. J. (1981) Structural and chemical variations in pyroxenes. Am. Mineral. 66, 1-50.Google Scholar
Carpenter, M. A. (1981) Time-temperature-transformation (TIT) analysis of cation disordering in omphacite. Contrib. Mineral. Petrol. 78, 433-40.CrossRefGoogle Scholar
Carpenter, M. A. (1983) Microstructures in sodic pyroxenes: implications and applications. Period. Mineral. 52, 271-301.Google Scholar
Carpenter, M. A. (1988) Thermochemistry of aluminium/silicon ordering in feldspar minerals. In Physical properties and thermodynamic behaviour of minerals (Salje, E., ed.. NA TO ASI Series C 225, Reidel, 265–323.CrossRefGoogle Scholar
Carpenter, M. A. and Putnis, A. (1985) Cation order and disorder during crystal growth: some implications for natural mineral assemblages. In Metamorphic reactions (Thompson, A. B. and Rubie, D. C., eds.). Advances in Physical Geochemistry 4, Springer-Verlag, 1–26.CrossRefGoogle Scholar
Carpenter, M. A., Navrotsky, A. and McConnell, J. D. C. (1983) Enthalpy effects associated with Al/Si ordering in anhydrous Mg-cordierite. Geochim. Cosmochim. Acta 47, 899-906.CrossRefGoogle Scholar
Carpenter, M. A., Domeneghetti, M. C. and Tazzoli, V. (1989a) Application of Landau theory to cation ordering in omphacite, I. Equilibrium behaviour. Euro. J. Mineral. (submitted).CrossRefGoogle Scholar
Carpenter, M. A., Domeneghetti, M. C. and Tazzoli, V. (1989b) Application of Landau theory to cation ordering in omphacite, II. Kinetic behaviour. Ibid. (submitted).CrossRefGoogle Scholar
Christian, J. W. (1975) The theory of transformations in metals and alloys, Part L Equilibrium and general kinetic theory. (2nd ed.) Pergamon Press, 586 pp.Google Scholar
Cook, H. E. (1969) The kinetics of clustering and shortrange order in stable solid solutions. J. Phys. Chem. Solids 30, 2427-37.CrossRefGoogle Scholar
Cook, H. E. and Hilliard, J. E. (1969) Effect of gradient energy on diffusion in gold-silver alloys. J. Appl. Phys. 40, 2191-8.CrossRefGoogle Scholar
Cook, H. E., de Fontaine, D. and Hilliard, J. E. (1969) A model for diffusion on cubic lattices and its application to the early stages of ordering. Acta Met. 17, 765-73.CrossRefGoogle Scholar
Cowley, R. A. (1976) Acoustic phonon instabilities and structural phase transitions. Phys. Rev. B 13, 4877-85.CrossRefGoogle Scholar
Fleet, M. E., Herzberg, C. T., Bancroft, G. M. and Aldridge, L. P. (1978) Omphacite studies, I. The P2/n→ C2/c transformation. Am. Mineral. 63, 1100-6.Google Scholar
Folk, R., Iro, H. and Schwabl, F. (1976) Critical statics of elastic transitions. Z. Physik. B25, 69–81.CrossRefGoogle Scholar
de Fontaine, D. and Cook, H. E. (1971) Early-stage clustering and ordering kinetics in binary solid solutions. In Critical phenomena in alloys, magnets and superconductors (Mills, R. E., Ascher, E. and Jaffee, R. I., eds.) McGraw Hill, 257-75.Google Scholar
Ginzburg, V. L., Levanyuk, A. P. and Sobyanin, A. A. (1987) Comments on the region of applicability of the Landau theory for structural phase transitions. Ferroelectrics 73, 171-82.CrossRefGoogle Scholar
Glauber, R. J. (1963) Time-dependent statistics of the Ising model. J. Math. Phys. 4, 294-307.CrossRefGoogle Scholar
Goldsmith, J. R. and Laves, F. (1956) Crystallization of metastable disordered anorthite at ‘low temperatures’. Z. Kristallogr. 107, 396-405.CrossRefGoogle Scholar
Güttier, B., Salje, E. and Putnis, A. (1988) Structural states of Mg cordierite III: infrared spectroscopy and the nature of the hexagonal-modulated transition. Phys. Chem. Minerals 16, 365-73.Google Scholar
Heine, V. and McConnell, J. D. C. (1984) The origin of incommensurate structures in insulators. J. Phys. C 17, 1199-220.CrossRefGoogle Scholar
Hilliard, J. E. (1970) Spinodal decomposition. In Phase transformations (Aaronson, H. I., ed.), Am. Soc. Metals, 497–560.Google Scholar
Hono, K. and Hirano, K.-I. (1987) Early stages of decomposition of alloys (spinodal or nucleation). Phase Trans. 10, 223-55.CrossRefGoogle Scholar
Kroll, H. and Müller, W. F. (1980) X-ray and electron optical investigation of synthetic high-temperature plagioclases. Phys. Chem. Minerals 5, 255-77.Google Scholar
Landau, L. D. and Lifshitz, E. M. (1980) Statistical physics. ( 3rd ed. ) Landau and Lifshitz course of theoreticalphysics 5, Pergamon press, 544 pp.Google Scholar
Langer, J. S. (1971) Theory of spinodal decomposition in alloys. Ann. Phys. 65, 53-86.CrossRefGoogle Scholar
Laves, F. and Goldsmith, J. R. (1955) The effect of temperature and composition on the A1-Si distribution in anorthite. Z. Kristallogr. 106, 227-35.Google Scholar
Lifshitz, E. M. and Pitaevski, L. P. (1981) Physicalkinetics. Landau and Lifshitz course of theoretical physics 10, Pergamon Press, 452 pp.Google Scholar
McConnell, J. D. C. (1981) Time-temperature study of the intensity of satellite reflections in nepheline. Am. Mineral. 66, 990-6.Google Scholar
McConnell, J. D. C. (1985) Symmetry aspects of order-disorder and the application of Landau theory. In Microscopic to macroscopic (Kieffer, S. W. and Navrotsky, A., eds.), Min. Soc. Am. Reviews in Mineralogy 14, 165-86.CrossRefGoogle Scholar
McConnell, J. D. C. (1988) The thermodynamics of short range order. In Physical properties and thermodynamic behaviour of minerals (Salje, E., ed.). NATO ASI Series C 225, Reidel, 17–48.CrossRefGoogle Scholar
McConnell, J. D. C. and Heine, V. (1985) Incommensurate structure and stability of mullite. Phys. Rev. B 31, 6140-2.CrossRefGoogle ScholarPubMed
McLaren, A. C. (1984) Transmission electron microscope investigations of the microstructures of microclines. In Feldspars andfeldspathoids (Brown, W. L., ed.). NATO ASI Series C 137, Reidel, 373–409.CrossRefGoogle Scholar
Metiu, H., Kitahara, K. and Ross, J. (1976a) Stochastic theory of the kinetics of phase transitions. J. Chem. Phys. 64, 292-9.CrossRefGoogle Scholar
Metiu, H., Kitahara, K. and Ross, J. (1976b) A derivation and comparison of two equations (Landau-Ginzburg and Cahn) for the kinetics of phase transitions. Ibid. 65, 393-6.CrossRefGoogle Scholar
Paulson, W. H. and Hilliard, J. E. (1977) Interdiffusion in composition modulated copper-gold thin films. J. Appl. Phys. 48, 2117-23.CrossRefGoogle Scholar
Poon, W. C-K. and Salje, E. (1988) The excess optical birefringence and phase transition in sodium nitrate. J. Phys. C. 21, 715-29.CrossRefGoogle Scholar
Putnis, A. (1980a) Order-modulated structures and the thermodynamics of cordierite reactions. Nature 287, 128-31.CrossRefGoogle Scholar
Putnis, A. (1980b) The distortion index in anhydrous Mg-cordierite. Contrib. Mineral. Petrol. 74, 135-41.CrossRefGoogle Scholar
Putnis, A. (1988) Solid state NMR spectroscopy and phase transitions in minerals. In Physical properties and thermodynamic behaviour of minerals (Salje, E., ed.. NA TO AS1 Series C 225, Reidel, 325-58.Google Scholar
Putnis, A. and Angel, R. J. (1985) AI,Si ordering in cordierite using ‘magic angle spinning’ NMR. II: Models of Al,Si order from NMR data. Phys. Chem. Minerals 12, 217-22.CrossRefGoogle Scholar
Putnis, A. and Bish, D. L. (1983) The mechanism and kinetics of Al,Si ordering in Mg cordiedte. Am. Mineral. 68, 60-5.Google Scholar
Putnis, A. and McConnell, J. D. C. (1980) Principles of mineral behaviour, Blackwell, 257 pp.Google Scholar
Putnis, A., Fyfe, C. A. and Gobbi, G. C. (1985) AI,Si ordering in cordierite using magic angle spinning’ NMR. I: Si29 spectra of synthetic cordierites. Phys. Chem. Minerals 12, 211-6.CrossRefGoogle Scholar
Putnis, A., Salje, E., Redfern, S. A. T., Fyfe, C. A. and Strobl, H. (1987) Structural states of Mg-cordierite I: Order parameters from synchrotron X-ray and NMR data. Ibid. 14, 446-54.CrossRefGoogle Scholar
Redfern, S. A. T. and Salje, E. (1987) Thermodynamics of plagioclase II: Temperature evolution of the spontaneous strain at the I1 ⇄ P1 phase transition in anorthite. Ibid. 14, 189-95.Google Scholar
Redfern, S. A. T. and Salje, E. (1988) Spontaneous strain and the ferroelastic phase transition in As2O5. J. Phys. C 21, 277-85. Google Scholar
Redfern, S. A. T. and Salje, E. and Navrotsky, A. (1989) High-temperature enthalpy at the orientational order-disorder transition in calcite: implications for the calcite/aragonite phase equilibrium. Contrib. Mineral. Petrol: 101, 479-84.CrossRefGoogle Scholar
Reeder, R. J., Redfern, S. A. T. and Salje, E. (1988) Spontaneous strain at the structural phase transition in NaNO 3. Phys. Chem. Minerals 15, 605-11.CrossRefGoogle Scholar
Ribbe, P. H. (1983a) Chemistry, structure and nomenclature of feldspars. In Feldspar mineralogy (2nd ed.) (Ribbe, P. H., ed.) Min. Soc. Am. Reviews in Mineralogy 2, 1-19.CrossRefGoogle Scholar
Ribbe, P. H. (1983b) Aluminum-silicon order in feldspars; domain textures and diffraction patterns. Ibid. 21-55.CrossRefGoogle Scholar
Rossi, G., Smith, D. C., Ungaretti, L. and Domeneghetti, M. C. (1983) Crystal-chemistry and cation ordering in the system diopside-jadeite: a detailed study by crystal structure refinement. Contrib. Mineral. Petrol. 83, 247-58.CrossRefGoogle Scholar
Salje, E. (1985) Thermodynamics of sodium feldspar I: order parameter treatment and strain induced coupling effects. Phys. Chem. Minerals 12, 93-8.CrossRefGoogle Scholar
Salje, E. (1987a) Structural states of Mg-cordierite II: Landau theory. Ibid. 14, 455-60.CrossRefGoogle Scholar
Salje, E. (1987b) Thermodynamics of plagioclase I: Theory of the I1 ⇄ P1 phase transition in anorthite and Carich plagioclase. Ibid. 14, 181-8.Google Scholar
Salje, E. (1988a) Kinetic rate laws as derived from order parameter theory I: Theoretical concepts. Ibid. 15, 336-48.CrossRefGoogle Scholar
Salje, E. (1988b) Structural phase transitions and specific heat anomalies. In Physical properties and thermodynamic behaviour of minerals (E. Salje, , ed.), NA TO ASI Series C 225, Reidel, 75–118.CrossRefGoogle Scholar
Salje, E. and Devarajan, V. (1986) Phase transitions in systems with strain-induced coupling between two order parameters. Phase Trans. 6, 235-48.CrossRefGoogle Scholar
Salje, E. and Wruck, B. (1988) Kinetic rate laws as derived from order parameter theory II: Interpretation of experimental data by Laplace-transformation, the relaxation spectrum, and kinetic gradient coupling between two order parameters. Phys. Chem. Minerals, 16, 140-7.CrossRefGoogle Scholar
Salje, E., Kuscholke, B., Wruck, B. and Kroll, H. (1985) Thermodynamics of sodium feldspar II: Experimental results and numerical calculations. Ibid. 12, 99-107.CrossRefGoogle Scholar
Salje, E., Bismayer, U. and Jansen, M. (1987) Temperature evolution of the ferroelastic order parameter of As2O5 as determined from optical birefringence. J. Phys. C. 20, 3613-20.Google Scholar
Smith, J. V. (1983) Phase equilibria of plagioclase. In Feldspar mineralogy (2nd ed.) (Ribbe, P. H., ed.), Min. Soc. Am. Reviews in Mineralogy 2, 223-39.CrossRefGoogle Scholar
Smith, J. V. (1984) Phase relations of plagioclase feldspars. In Feldspars and feldspathoids (Brown, W. L., ed.). NATO ASI Series C 137, Reidel, 55–94.CrossRefGoogle Scholar
Smith, J. V. and Brown, W. L. (1988) Feldspar minerals 1 (2nd ed.), Crystal structures, physical, chemical and microtexturalproperties. Springer-Verlag, 828 pp.CrossRefGoogle Scholar
Yamauchi, H. and de Fontaine, D. (1974) Kinetics of order-disorder. In Order-disorder transformations in alloys (Warlimont, H., ed.), Springer-Verlag, 148-78.CrossRefGoogle Scholar
Yund, R. A. (1983) Microstructure, kinetics and mechanisms of alkali feldspar exsolution. In Feldspar mineralogy (Ribbe, P. H., ed.), Min. Soc. Am. Reviews in Mineralogy 2, 177–202. CrossRefGoogle Scholar
Yund, R. A. (1984) Alkali feldspar exsolution: kinetics and dependence on alkali interdiffusion. In Feldspars and feldspathoids (Brown, W. L., ed.) NATO ASI Series C 137, Reidel, 281–315.CrossRefGoogle Scholar