Hostname: page-component-cc8bf7c57-fxdwj Total loading time: 0 Render date: 2024-12-11T22:17:30.740Z Has data issue: false hasContentIssue false
  • English
  • Français

A neutron powder diffraction determination of the thermal expansion tensor of crocoite (PbCrO4) between 60 K and 290 K

Published online by Cambridge University Press:  05 July 2018

Kevin S. Knight
Kevin S. Knight*
Affiliation:
ISIS Science Division, Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire, OXI1 0QX UK
Get access Rights & Permissions [Opens in a new window]

Abstract

The thermal expansion tensor of crocoite has been determined from high-resolution neutron time-of-flight powder diffraction data. The temperature dependence of the lattice constants between 4.5 K and 290 K have been fitted to a quasi-harmonic Einstein model, and the temperature dependence of the thermal expansion tensor has been calculated for 60 K ≤ T ≤ 290 K. The magnitudes of the principal expansivities and their orientation exhibit saturation behaviour for temperatures above 300 K. The predicted saturated expansion coefficients are α11 = 33.1(1) × 10−6K−1, α22 = 15.72(3) × 10−6K−1, α33 = 3.36(1) × 10−6K−1, with α22 parallel to b and α11 lying at an angle of −37.86(5)° to c for the P21/n setting of the crystal structure. 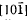The direction of maximum expansion is approximately parallel to both and the least-squares line passing through the projection of the chromium atoms on (010). The direction of minimum expansion lies approximately parallel to [101]. No evidence was found for either a structural or magnetic phase transition between 4.5 K and 300 K.

Keywords

crocoitethermal expansivityneutron diffractionPbCrO4
Type
Mineralogy
Information
Mineralogical Magazine , Volume 60 , Issue 403 , December 1996 , pp. 963 - 972
Copyright
Copyright © The Mineralogical Society of Great Britain and Ireland 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrahams, S.C. and Bernstein, J.L. (1974) Piezoelectric nonlinear optic CuGaSe2 and CdGeAs2: crystal structure, chalcopyrite microhardness, and sublattice distortion. J. Chem. Phys., 61, 1140–6.CrossRefGoogle Scholar
Brill, R. (1931) Uber das gitter von bleichromat. Zeit. Kristallogr., 77, 506.Google Scholar
Brody, S.B. (1942) An X-ray investigation of the structure of lead chromate. J. Chem. Phys., 10, 650–2.CrossRefGoogle Scholar
Collotti, G., Conti, L. and Zocchi, M. (1959) The structure of the orthorhombic modification of lead chromate PbCrO4. Acta Crystallogr., 12, 416.CrossRefGoogle Scholar
David, W.I.F., Ibberson, R.M. and Matthewman, J.C. (1992) Profile analysis of neutron powder diffraction data at ISIS. Rutherford Appleton Laboratory Report RAL-92-032.Google Scholar
David, W.I.F., Ibberson, R.M. and Matsuo, T. (1993) High resolution neutron powder diffraction: a case study of the structure of C60. Proc. Roy. Soc. Lond.A, 442 129-46.Google Scholar
Ibberson, R.M., David, W.I.F. and Knight, K.S. (1992) The high resolution powder diffractometer (HRPD) at ISIS – a user guide. Rutherford Appleton Laboratory Report RAL-92-031.Google Scholar
Ikeda, S. and Carpenter, J.M. (1985) Wide-energy- range, high-resolution measurements of neutron pulse shapes of polyethylene moderators. Nuclear Instruments and Methods in Physics Research A239, 536-44.CrossRefGoogle Scholar
Jaeger, F.M. and Germs, H.C. (1921) Über die binären systeme der sulfate, chromate, molybdate und wolframate des bleies. Zeit. Anorg. Chern., 119, 145–73.CrossRefGoogle Scholar
lessen, S.M. and Kiippers, H. (1991) The precision of thermal-expansion tensors of triclinic and monoclinic crystals. J. Appl. Crystallogr., 24, 239–42.Google Scholar
Johnson, M.W. and David, W.I.F. (1985) HRPD: The high resolution powder diffractometer at the SNS. Rutherford Appleton Laboratory Report RAL-85- 112.Google Scholar
Naray-Szabo, I. and Argay, G. (1965) Die krisrallstruk- tur des krokoits, PbCrO4. Acta Chimica Acad. Scientiarum Hungarae, 40, 283–8.Google Scholar
Palache, C., Berman, H. and Frondel, C. (1951) The system of mineralogy of James Dwight Dana and Edward Salisbury Dana volume 2, 7th edition. John Wiley and Sons.Google Scholar
Pistorius, C.W.F.T. and Pistorius, M.C. (1962) Lattice constants and thermal-expansion properties of the chromates and selenates of lead, strontium and barium. Zeit. Kristallogr., 117, 259–71.CrossRefGoogle Scholar
Popovkin, B.A. and Simanov, Y.P. (1962) An X-ray diffraction study of the two modifications of lead selenate. Zh. Neorgan. Khim., 7, 1743–4.Google Scholar
Quareni, S. and De Pieri, R. (1964) La struttura della crocoite, PbCr04. Rendiconti della Societa Mineraloica Italiana, 20, 235–50.Google Scholar
Quareni, S., and De Pieri, R. (1965) A three-dimensional refinement of the structure of crocoite, PbCrO4. Acta Crystallogr. 19, 287–9.CrossRefGoogle Scholar
Quittner, F., Sagpir, J. and Rassudowa, N. (1932) Die rhombische modifikation des bleichromates. Zeit. Anorg, Chem., 204, 315–7.CrossRefGoogle Scholar
Rietveld, H.M. (1967) Line profiles of neutron powder- diffraction peaks for structure refinement. Acta Crystallogr., 22, 151–2.CrossRefGoogle Scholar
Rietveld, H.M. (1969) A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr., 2, 65–71.CrossRefGoogle Scholar
Sears, V.F. (1992) Neutron scattering lengths and cross sections. Neutron News, 3, 26–37.CrossRefGoogle Scholar
Von Gliszczynski, S. (1939) Beitrag zur isomorphie von monazit und krokoit. Zeit. Kristallogr., 101, 1 – 16.Google Scholar
Wagner, H., Haug, R. and Zipfel, M. (1932) Die modifikation des bleichromats. Zeit. Anorg. Chem., 208, 249–54.CrossRefGoogle Scholar
Young, R.A. (editor) (1993) The Rietveld Method. Oxford University Press Google Scholar