Using the polynomial method of Dvir [On the size of Kakeya sets in finite fields. Preprint], we establish optimal estimates for Kakeya sets and Kakeya maximal functions associated to algebraic varieties W over finite fields F. For instance, given an (n−1)-dimensional projective variety W⊂¶n(F), we establish the Kakeya maximal estimate for all functions f:Fn→R and d≥1, where for each w∈W, the supremum is over all irreducible algebraic curves in Fn of degree at most d that pass through w but do not lie in W, and with Cn,W,d depending only on n,d and the degree of W; the special case when W is the hyperplane at infinity in particular establishes the Kakeya maximal function conjecture in finite fields, which in turn strengthens the results of Dvir.

It is shown here that given a discrete (and infinite) set of points in the plane, it is possible to arrange them on a polygonal path so that every angle on the polygonal path is at least 9∘. This has been known to hold for finite sets (with 20∘). The main result holds for discrete sets in higher dimensions as well, with a smaller bound on the angle.

We obtain the formula for the twisted harmonic second moment of the L-functions associated with primitive Hecke eigenforms of weight 2. A consequence of our mean-value theorem is reminiscent of recent results of Conrey and Young on the reciprocity formula for the twisted second moment of Dirichlet L-functions.

Given some unit vectors a1,…,am∈ℝn that span all ℝn and some positive numbers θ1,…,θm, we consider for every p≥1 the convex body We will give some upper bounds for the volume of Kp and some lower bounds for the volume of its polar, depending on some parameters, which improve the ones obtained using the Brascamp–Lieb inequality. We will also see how the best choice of these parameters is related to the transformation which takes Kp to a special position which, for instance, when p=∞, is John’s position.

We find the almost-sure Hausdorff and box-counting dimensions of random subsets of self-affine fractals obtained by selecting subsets at each stage of the hierarchical construction in a statistically self-similar manner.

The Hausdorff dimension and measure of the set of simultaneously ψ-approximable points lying on integer polynomial curves is obtained for sufficiently small error functions.

A line that intersects every member of a finite family F of convex sets in the plane is called a common transversal to F. In this paper we study some basic properties of T(k)-families: finite families of convex sets in the plane in which every subfamily of size at most k admits a common transversal. It is known that a T(k)-family admits a partial transversal of size α∣F∣ for some constant α(k) which is independent of F. Here it will be shown that (2/(k(k−1)))1/(k−2)≤α(k)≤((k−2)/(k−1)), which are the best bounds to date.

Gravity and surface-tension effects are examined for inviscid–inviscid interactions between two fluids close to a wall. The ratios of density and viscosity of the two fluids are taken to be small. A nonlinear integro–differential equation is found to govern the near-wall flow velocity, interface shape and pressure; analysis, computation and comparisons are then applied. Travelling-state solutions are of particular interest.

We prove algebraic transformations for the generating series of three Apéry-like sequences. As application, we provide new binomial representations for the sequences. We also illustrate a method that derives three new series for 1/π from a classical Ramanujan’s series.

We study the variance of the fluctuations in the number of lattice points in a ball and in a thin spherical shell of large radius centred at a Diophantine point.

We prove that for any given integer c≥0 any metric space on n points may be isometrically embedded into ln−c∞ provided n is large enough.

Interactions between a finite number of bodies and the surrounding fluid, in a channel for instance, are investigated theoretically. In the planar model here the bodies or modelled grains are thin solid bodies free to move in a nearly parallel formation within a quasi-inviscid fluid. The investigation involves numerical and analytical studies and comparisons. The three main features that appear are a linear instability about a state of uniform motion, a clashing of the bodies (or of a body with a side wall) within a finite scaled time when nonlinear interaction takes effect, and a continuum-limit description of the body–fluid interaction holding for the case of many bodies.

Carathéodory’s theorem on small witnesses for convex hulls of sets is shown to have a natural analogue for finitely supported measures. Contrast is drawn with the much larger witnesses required for multisets, as shown by Bárány and Perles.

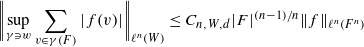
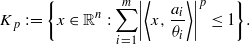
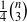It is well known that a tournament (complete oriented graph) on n vertices has at most directed triangles, and that the constant is best possible. Motivated by some geometric considerations, our aim in this paper is to consider some “higher order” versions of this statement. For example, if we give each 3-set from an n-set a cyclic ordering, then what is the greatest number of “directed 4-sets” we can have? We give an asymptotically best possible answer to this question, and give bounds in the general case when we orient each d-set from an n-set.

We prove that there are permutation classes (hereditary properties of permutations) of every growth rate (Stanley–Wilf limit) at least λ≈2.48187, the unique real root of x5−2x4−2x2−2x−1, thereby establishing a conjecture of Albert and Linton.