Research Article
Kinematic measures for sets of colliding convex Bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-12
-
- Article
- Export citation
A support characterization of zonotopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-16
-
- Article
- Export citation
On three sets with no point in common
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-23
-
- Article
- Export citation
Laminar flow over a small unsteady hump on a flat plate
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-35
-
- Article
- Export citation
Extremal self-dual lattices exist only in dimensions 1 to 8, 12, 14, 15, 23, and 24
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 36-43
-
- Article
- Export citation
Extreme forms and cyclotomy
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 44-56
-
- Article
- Export citation
One-class genera of positive quadratic forms in nine and ten variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-67
-
- Article
- Export citation
Euler factors for p-adic L-functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-75
-
- Article
- Export citation
Fractional parts of several polynomials—II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-93
-
- Article
- Export citation
On the minimum of zero indefinite binary quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-106
-
- Article
- Export citation
Continuants with bounded digits—II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-109
-
- Article
- Export citation
A triangulation criterion
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 110-114
-
- Article
- Export citation
Corrigenda
Correction to On the first end invariant of an exact sequence
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 115
-
- Article
-
- You have access
- Export citation
Research Article
Lebesgue density influences Hausdorff measure; large sets surface-like from many directions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-119
-
- Article
- Export citation
An example concerning completion regular measures, images of measurable sets and measurable selections
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-124
-
- Article
- Export citation
Some intersection and union theorems for several families of finite sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-128
-
- Article
- Export citation
Waves and conjugate streams with vorticity
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-150
-
- Article
- Export citation
Non-existence of large eigenvalues of a third order differential equation
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-159
-
- Article
- Export citation
Lagrange's theorem for weak functions of several variables
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 160-178
-
- Article
- Export citation
Front matter
MTK volume 25 issue 1 Front Matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

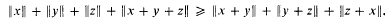
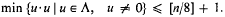
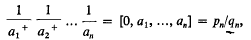
 supporting a Radon probability measure μ and a continuous map ø :
supporting a Radon probability measure μ and a continuous map ø : 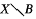 and
and 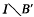 homeomorphic
homeomorphic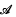 is a collection of distinct subsets of {1, …,
is a collection of distinct subsets of {1, …, 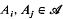 ,
, 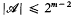 .
.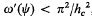 , where
, where