Research Article
One-class genera of positive ternary quadratic forms—II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
-
- Article
- Export citation
An Ω-result for the coefficients of cusp forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 12-19
-
- Article
- Export citation
On a theorem of Heilbronn
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 20-28
-
- Article
- Export citation
On a metrical theorem of Weyl
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-33
-
- Article
- Export citation
On the theory of stress concentration for shear-strained prismatical bodies with a non-linear stress-strain law
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-42
-
- Article
- Export citation
A note on universal sets for classes of countable Gδ'S
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-45
-
- Article
- Export citation
On waves in a thin rotating spherical shell of slightly viscous fluid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 46-59
-
- Article
- Export citation
On the first end invariant of an exact sequence
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-70
-
- Article
- Export citation
On the norms of algebraic integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-80
-
- Article
- Export citation
A lattice-point problem in hyperbolic space
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-88
-
- Article
- Export citation
Dense primitive polynomial sequences
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-91
-
- Article
- Export citation
Zero-free regions for ζ(s)
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 92-96
-
- Article
- Export citation
Index
Index to volume 22
-
- Published online by Cambridge University Press:
- 26 February 2010, p. i
-
- Article
- Export citation
Front matter
MTK volume 22 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

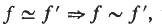 , where
, where 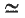 denote equivalence and semi-equivalence respectively. Trivially, it suffices to find the primitive
denote equivalence and semi-equivalence respectively. Trivially, it suffices to find the primitive 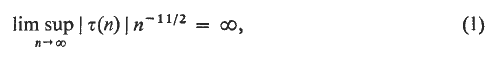
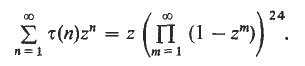
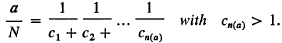
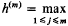 h
h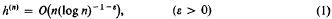
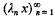
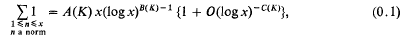
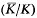 and Gal
and Gal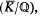 , where
, where 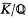 is the normal hull of
is the normal hull of 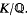 .
.